- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n
( 3 )
取极限
:d
m
a
x
{
D
的
i
直
径
}
,V
lim d0
i1
f ( i, i ) i
若 此 极 限 与 分 割 方 法 和 ( i , i ) Di 取 法 无 关 ,则 称
此 极 限 为 f (x, y) 在 区 域 D 上 的 二 重 积 分 (可 积 ),记 作
f (x, y)d 或 f (x, y)dxdy
y
1
D2 D3
D1 y=x3
-1 D4 O
1x
(图7-12)
作业:习题 7-2
3(3)(4); 4(3)(4); 5(3)(4)(5);
y 1
D
O
y=x2 x (图7-8)
例73 计算x2dxdy,其中D由曲线 Dyx2和yຫໍສະໝຸດ x2所围成的闭区域 .y 2
AD
B
-1 O 1 x(图7-9)
例74 计算ex2dxdy,其中D由x轴, D
直线x1及yx围成.
y
1 y=x
D
O
1
x (图7-10)
补充例子 : 1.计算下列二重积分(习题7-2:5(1)(2)):
若 f (x, y) f (x, y),则 f (x, y)d 2 f (x, y)d
D
D2
例75 计算I (xyx3ey)dxdy, D
其中D为下半圆
D{(x, y) x2 y2 4, y0}
y
-2
2
O
x
D
(图7-11)
例76 设D为yx3,x1,y1所 围 成
的 闭 区 域 ,求I[2x2ysin(xy)]dxdy. D
Y-型域的计算方法
f (x, y)dxdy
d
dy
2(y)
f
(x, y)dx
D
c 1(y)
d
[
2(y) f (x, y)dx]dy
c 1(y)
当D不是X型域或Y型域时,可将D分解
为X型域和Y型域来计算.
例72 计 算xy2dxdy,其 中D由y轴 ,
D
直 线y1及 抛 物 线yx2(x0)围 成 .
y y 2(x)
D
y 1(x)
a
b
y d
D x 1(y)
c
x
x 2(y)
x
X-型域的计算方法
(1) 取 定 x [ a , b ], 考 虑 一 元 函 数 g ( y ) f ( x , y )
在 [ 1 ( x ), 2 ( x )] 上 的 曲 边 梯 形 的 面 积 :
S ( x ) 2 ( x ) g ( y ) d y 2 ( x ) f ( x , y ) d y
f ( i ) xi
几 何 意 义 :曲 边 梯 形 的 面 积 .
2. 二 重 积 分 的 定 义 : z f (x, y) ((x, y) D )
(1) 分 割 : 将 区 域 D 分 割 成 若 干 小 区 域 块 ,
i 为 第 i 个 小 区 域 Di 的 面 积.
n
( 2 ) 求 和 : 取 ( i , i ) D i , 作 和 : f ( i , i ) i i1
(1)
11
dy
x3 1dx; (2)
11
dx
xy dy
0
y
0 x2 1 y3
2. 设 f (x, y) 连续,且 f (x, y) xy f (u, v)dudv, D 其中 D 是由 y 0, y x2, x 1 所围成,则 f (x, y) ________ .
3. 计算 V x2 y2 1dxdy,其中 D {(x, y) 0 x 1, 0 y 1} D
4. 计算 emax{x2,y2}d ,其中 D {(x, y) 0 x 1, 0 y 1}. D
函数关于x或y为奇(偶)函数的积分
当z f (x, y) 关于x 或 y 为奇函数
y
(或偶函数)时,积分可以简化.
D1 D2 x
1.积分区域关于y 轴对称:
若 f (x, y) f (x, y),则 f (x, y)d 0; D
1 ( x )
1 ( x )
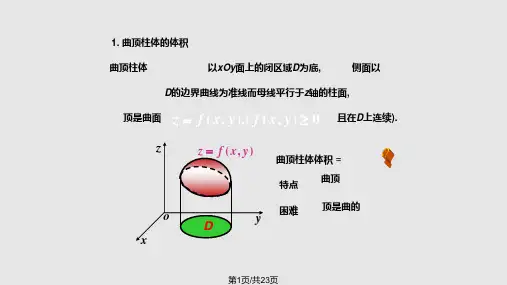
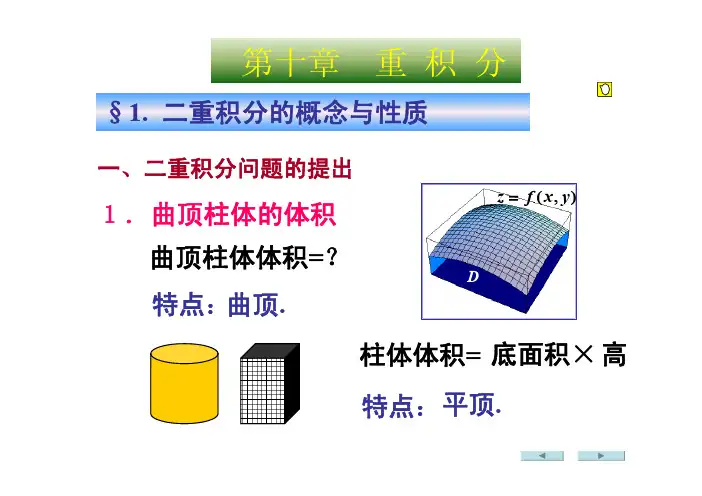
(2) 曲 顶 柱 体 的 体 积 :
V
b
S (x)dx
b
[
2 (x) f ( x , y )d y ]d x
a
a 1(x)
b
dx
2(x) f (x, y)dy.
a
1 ( x )
则
f (x, y)dxdy
b
dx
2(x) f (x, y)dy
D
a
1 ( x )
D
D
几 何 意 义 :曲 顶 柱 体 的 体 积 .
7.2 二重积分的计算
7.2.2 直 角 坐 标 系 下 二 重 积 分 的 计 算 一 .X -型 积 分 区 域 和 Y -型 积 分 区 域 : 1. X-型域: D {(x, y) 1(x) y 2 (x), a x b} 2. Y-型域: D {(x, y) 1( y) x 2( y),c y d} 3. 可分解为X 型域和Y 型域的区域
第7章 多元函数积分学
本章主要讲授:
1. 二重积分 2. 三重积分 3. 第一类曲线积分 4. 第一类曲面积分 5. 积分在几何,物理中的应用
7.1 二重积分的定义及性质
1. 一 元 函 数 定 积 分 的 定 义 :y f (x)(a x b)
( 1 ) 分 割 : a x0 x1 xn b , xi xi xi1
n
( 2 ) 求 和 : 取 i [ x i 1 , x i ] , 作 和 : f ( i ) x i i1
n
( 3 )
取 极 限: I
lim 0
i1
f ( i ) xi.
若 极 限 I 与 分 割 方 法 无 关 ,与 i 取 法 无 关 ,
则
b
n
a
f (x)dx I
lim 0 i1