【教师】一次函数动点问题教师版
- 格式:docx
- 大小:328.26 KB
- 文档页数:13

一次函数之动点问题(讲义)一、知识点睛动点问题的特征是速度已知,主要考查运动的过程. 1. 一次函数背景下研究动点问题的思考方向:①把函数信息(坐标或表达式)转化为基本图形的信息; ②分析运动过程,注意状态转折,确定对应的时间范围; ③画出符合题意的图形,研究几何特征,设计解决方案. 2. 解决具体问题时会涉及线段长的表达,需要注意两点:①路程即线段长,可根据s =vt 直接表达已走路程或未走路程;②根据研究几何特征需求进行表达,既要利用动点的运动情况,又要结合基本图形信息.二、精讲精练1. 如图,在平面直角坐标系中,O 为坐标原点,直线334y x =-+与x 轴、y 轴分别交于A ,B 两点.点P 从点A 出发,以每秒1个单位的速度沿射线AO 匀速运动,设点P 的运动时间为 t 秒.(1)求OA ,OB 的长.(2)过点P 与直线AB 垂直的直线与y 轴交于点E ,在点P 的运动过程中,是否存在这样的点P ,使△EOP ≌△AOB ?若存在,请求出t 的值;若不存在,请说明理由.y xOBA2. 如图,直线=3+43y x 与x 轴、y 轴分别交于A ,B 两点,直线BC 与x 轴交于点C ,∠ABC =60°.(1)求直线BC 的解析式.(2)若动点P 从点A 出发沿AC 方向向点C 运动(点P 不与点A ,C 重合),同时动点Q 从点C 出发沿折线CB —BA 向点A 运动(点Q 不与点A ,C 重合),动点P 的运动速度是每秒1个单位长度,动点Q 的运动速度是每秒2个单位长度.设△APQ 的面积为S ,运动时间为t 秒,求S 与t 之间的函数关系式,并写出自变量t 的取值范围. (3)当t =4时,y 轴上是否存在一点M ,使得以A ,Q ,M 为顶点的三角形为等腰三角形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.C ABOxy CABOxy3. 如图,在直角梯形COAB 中,OC ∥AB ,以O 为原点建立平面直角坐标系,A ,B ,C三点的坐标分别为A (8,0),B (8,11),C (0,5),点D 为线段BC 的中点.动点P 从点O 出发,以每秒1个单位的速度,沿折线OA —AB —BD 的路线运动,至点D 停止,设运动时间为t 秒.(1)求直线BC 的解析式.(2)若动点P 在线段OA 上运动,当t 为何值时,四边形OPDC 的面积是梯形COAB 面积的14?(3)在动点P 的运动过程中,设△OPD 的面积为S ,求S 与t 之间的函数关系式,并写出自变量t 的取值范围.P DCxA OByyBO A xCD4. 如图,直线334y x =-+与x 轴交于点A ,与直线33y x =交于点P . (1)求点P 的坐标. (2)求△OP A 的面积.(3)动点E 从原点O 出发,以每秒1个单位的速度沿OA 方向向终点A 运动,过点E 作EF ⊥x 轴交线段OP 或线段P A 于点F ,FB ⊥y 轴于点B .设运动时间为t 秒,矩形OEFB 与△OP A 重叠部分的面积为S ,求S 与t 之间的函数关系式.PFE xA OB y5. 如图,直线l 的解析式为y =-x +4,它与x 轴、y 轴分别交于A ,B 两点,平行于直线l的直线m 从原点O 出发,沿x 轴的正方向以每秒1个单位长度的速度运动,它与x 轴、y 轴分别交于M ,N 两点,设运动时间为t 秒(0< t <4). (1)求A ,B 两点的坐标;(2)用含t 的代数式表示△MON 的面积S 1;(3)以MN 为对角线作矩形OMPN ,记△MPN 和△OAB 重 叠部分的面积为S 2,试探究S 2与t 之间的函数关系式.xy OABm l PM N【参考答案】1.(1)OA =4,OB =3; (2)t =1或t =7 2.(1)343y x =-+(2)223(04)2343(48)2t t S t t t ⎧<⎪⎪=⎨⎪-+<<⎪⎩≤(3)123(0438)(0438)(043)M M M -+-,或,或,443(0)3M 或,3.(1)354y x =+(2)32t =(3)4(08)248(819)248(1924)t t S t t t t <⎧⎪=-+<⎨⎪-+<<⎩≤≤4.(1)(33)P , (2)23(3)223(03)653163243(34)2tt S t t t ⎧<⎪⎪=⎨⎪-+-<<⎪⎩≤5.(1)(40)(04)A B ,,,(2)2112S t =(3)2221(02)2388(24)2t t S t t t ⎧<⎪⎪=⎨⎪-+-<<⎪⎩≤。
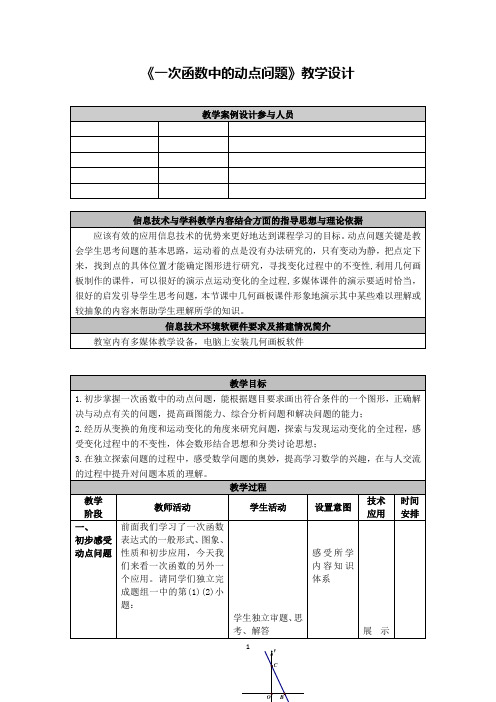

精品文档一次函数的动点问题类型一面积问题23.如图,直线y3x1和两坐标轴交于点A,B,以线段AB为边在第一象限作等边三角形ABC,存在点31ABC的面积与ABP的面积相等,求m的值。
P(m,),使2练习1如图,直线y1x1和两坐标轴交于点A,B,把线段AB绕点A顺时针旋转90°得到线段AB'.〔1〕求直线AB'的解析式。
2(2)假设动点C(1,a)使得S ABC S ABB'的面积相等,求a的值。
.练习2如图,一次函数y 1xb的图像过A(2,3),AB x轴于点B,连接OA。
〔1〕求一次函数解析式。
2〔2〕设点P为直线y1x b上一点,且在第一象限内,经过点P〔不与A重合〕作x轴的垂线,2假设SPOQ S AOB,求点P的坐标。
练习3A(0,2),B(2,0),C(0,0)三个点为顶点的三角形被直线yaxa分成两局部,〔1〕填空:不管a为何值,直线yax a必定经过一顶点C,那么该顶点为。
〔2〕假设所分的两局部面积之比为1:7,求a的值。
.如图,直线y2x4的图像交两坐标轴于点A,B ,点C 为OB 的中点,直线l 经过点C ,与AB 交于点D,把AOB 的面积分为1:2,求直线l 的解析式。
如图,直线y2x 3与x 轴交于点A ,与y 轴交于点B 。
〔1〕求点A,B 的坐标。
〔2〕过点B 作直线BP 与x 轴交于点P ,假设S ABP15,求直线BP 的解析式。
4.二动点问题一条直线上顺次有A,B,C三个港口,甲乙两船分别从A,B港口出发,沿直线行驶到C港口,最终到达C 港口在一条直线上依次有A、B、C三个港口,甲乙两船同时分别从A、B港口出发,沿直线匀速驶向C 港.最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2〔km〕,y1、y2与x的函数关系如下图.〔1〕填空:A、C两港口间的距离____km,a=_____;2〕求图中点P的坐标,并解释该点坐标所表示的实际意义;3〕假设两船的距离不超过10km时能够相互望见,求甲、乙两船可以相互望见时,x的取值范围.两城A,B间的公路长为450千米,甲、乙两车同时从A城出发沿这一公路驶向B城,甲车到达B城1小时后沿原路返回.如图是它们离A城的路程y〔千米〕与行驶时间x〔小时〕之间的函数图像.〔1〕求甲车返回过程中y与x之间的函数解析式,并写出x的取值范围;〔2〕乙车与返回的甲车相遇距离B城还有多远?.精品文档特殊三角形问题A(1,0),B(4,4),在y轴上找一点C,使得ABC为等腰三角形,求出点C的坐标。

专题06 一次函数中的动点问题知识对接考点一、怎样解一次函数图象的平移问题 1、直线的平移规律(1)直线)0(≠+=k b kx y 可由直线)0(≠=k kx y 向上或向下平移得到,当b>0时,将直线kx y =沿y 轴向上平移b 个单位长度得到直线b kx y +=;当b<0时,将直线kx y =沿y 轴向下平移b 个单位长度得到直线b kx y +=.简而言之,“上加下减”(2)直线)(m x k y +=可由直线kx y =向左或向右平移得到,当m<0时,将直线kx y =沿x 轴向右平移m 个单位长度,可得到直线)(m x k y +=;当>0时,将直线kx y =沿x 轴向左平移m 个单位长度,可得到直线)(m x k y +=,简而言之,“左加右减”(3)一次函数的图象平移,不会改变图象的形状与大小,平移后的图象与原来的图象平行,直线平移后的解析式中,k 的值不变,只有b 的值发生变化.专项训练一、单选题1.一次函数y =kx +b 的图象是由函数y =2x 的图象向左平移3个单位长度后得到的,则该一次函数的解析式为( ) A .y =2x +6 B .y =﹣2x +6C .y =2x ﹣6D .y =﹣2x ﹣6【答案】A 【分析】利用一次函数平移规律,左加右减得出答案. 【详解】解:由题意可得:y =2(x +3)=2x +6. 故选:A . 【点睛】本题考查待定系数法求一次函数解析式,注意平移不影响k 的值是关键.2.若一次函数的y =kx +b (k <0)图象上有两点A (﹣2,y 1)、B (1,y 2),则下列y 大小关系正确的是( ) A .y 1<y 2 B .y 1>y 2C .y 1≤y 2D .y 1≥y 2【答案】B首先观察一次函数的x 项的系数,当x 项的系数大于0,则一次函数随着x 的增大而增大,当x 小于0,则一次函数随着x 的减小而增大.因此只需要比较A 、B 点的横坐标即可. 【详解】解:根据一次函数的解析式y =kx +b (k <0) 可得此一次函数随着x 的增大而减小 因为A (﹣2,y 1)、B (1,y 2), 根据-2<1,可得12y y > 故选B . 【点睛】本题主要考查一次函数的一次项系数的含义,这是必考点,必须熟练掌握.一次函数的x 项的系数,当x 项的系数大于0,则一次函数随着x 的增大而增大,当x 小于0,则一次函数随着x 的增大而减小.3.已知一次函数的图象过点(2,0)和点(1,1)-,则这个函数的解析式为( ) A .2y x =- B .2y x =+ C .2y x =-- D .2y x =--【答案】A 【分析】利用待定系数法即可求得函数的解析式. 【详解】设所求一次函数的解析式为:y =kx +b ,其中k ≠0 ∵直线y =kx +b 的图象过点(2,0)和点(1,1)-∵201k b k b +=⎧⎨+=-⎩ 解得:12k b =⎧⎨=-⎩ ∵y =x -2 故选:A . 【点睛】本题考查了用待定系数法求一次函数的解析式,其一般步骤是:设函数解析式y =kx +b ;根据条件得出关于k ,b 的方程组;解方程组;写出函数解析式,可简记为:设,代,解,答. 4.将一次函数1y x =-+的图象向上平移3个单位,则新的一次函数的解析式为( ) A .21y x =+ B .4y x =--C .4y x =-+D .41y x =-+【答案】C直接根据“上加下减”的原则进行解答即可. 【详解】解:由“上加下减”的原则可知,将一次函数1y x =-+的图象向上平移3个单位, 所得的直线解析式为:13y x =-++, 即:4y x =-+, 故选:C . 【点睛】本题主要考查的是一次函数的图像与几何变换,熟知函数图像的平移法则是解答此题的关键. 5.定义:对于给定的一次函数y ax b =+(a 、b 为常数,且0a ≠,把形如()()00ax b x y ax b x ⎧+≥⎪=⎨--<⎪⎩的函数称为一次函数y ax b =+的“相依函数”,已知一次函数1y x =+,若点()2,P m -在这个一次函数的“相依函数”图象上,则m 的值是( ) A .1 B .2 C .3 D .4【答案】A 【分析】找出一次函数1y x =+的“相依函数”,再利用一次函数图象上点的坐标特征,即可求出m 的值. 【详解】解:一次函数1y x =+的“相依函数”为()()1010x x y x x ⎧+≥⎪=⎨--<⎪⎩,∵点P (−2,m )在一次函数的“相依函数”图象上, ∵m =−1×(−2)−1=1. 故选:A . 【点睛】本题考查了一次函数图象上点的坐标特征,根据“相依函数”的定义,找出一次函数1y x =+的“相依函数”是解题的关键.6.若把一次函数y =kx +b 的图象先绕着原点旋转180°,再向右平移2个单位长度后,恰好经过点A (4,0)和点B (0,﹣2),则原一次函数的表达式为( ) A .y =﹣12x ﹣1 B .y =﹣12x +1C .y =12x +1D .y =12x ﹣1【答案】C 【分析】设直线AB 的解析式为y =kx +b ,根据题意,得402k b b +=⎧⎨=-⎩,得到直线解析式为y =12x -2,将其向左平移2个单位,得到y =12x -1,绕着原点旋转180°,得解. 【详解】设直线AB 的解析式为y =kx +b ,根据题意,得402k b b +=⎧⎨=-⎩,解得122k b ⎧=⎪⎨⎪=-⎩, ∵直线解析式为y =12x -2,将其向左平移2个单位,得y =12(x +2)-2, 即y =12x -1,∵与y 轴的交点为(0,-1),与x 轴的交点为(2,0), ∵绕着原点旋转180°,∵新直线与与y 轴的交点为(0,1),与x 轴的交点为(-2,0), ∵设直线的解析式为y =mx +1, ∵-2m +1=0, 解得m =12, ∵y =12x +1, 故选C . 【点睛】本题考查了一次函数的图像平移,旋转问题,熟练掌握平移规律是解题的关键.7.数学课上,老师提出问题:“一次函数的图象经过点(3,2)A ,(1,6)B --,由此可求得哪些结论?”小明思考后求得下列4个结论:∵该函数表达式为24y x =-;∵该一次函数的函数值随自变量的增大而增大;∵点(2,44)P a a -该函数图象上;∵直线AB 与坐标轴围成的三角形的面积为8.其中正确的结论有( ) A .1个 B .2个C .3个D .4个【答案】C 【分析】已知一次函数过两个点A (3,2),B (-1,-6),可以用待定系数法求出关系式;根据关系式可以判定一个点(已知坐标)是否在函数的图象上;根据一次函数的增减性,可以判定函数值随自变量的变化情况,当k >0,y 随x 的增大而增大;根据关系式可以求出函数图象与x 轴、y 轴的交点坐标,进而可以求出直线AB 与坐标轴围成的三角形的面积,最后综合做出结论. 【详解】解:设一次函数表达式为y =kx +b ,将A (3,2),B (-1,-6)代入得:326k b k b +=⎧⎨-+=-⎩, 解得:k =2,b =-4,∵关系式为y =2x -4,故∵正确;由于k =2>0,y 随x 的增大而增大,故∵正确; 点P (2a ,4a -4),代入,得:2×2a -4=4a -4,∵其坐标满足y =2x -4,因此该点在此函数图象上;故∵正确; 令x =0,则y =-4,令y =0,则x =2,∵直线AB 与x 轴,y 轴的交点分别(2,0),(0,-4),因此与坐标轴围成的三角形的面积为:124482⨯⨯=≠,故∵错误;因此,∵∵∵均正确,∵不正确. 故选:C . 【点睛】本题考查待定系数法求函数关系式,一次函数的性质,一次函数图象的点的坐标特征,以及依据关系式求出函数图象与坐标轴的交点坐标,进而求出三角形的面积等知识点,在解题中渗透选择题的排除法,验证法.8.下列函数关系式:(1)y x =-;(2)1y x =-;(3)1y x=;(4)2y x ,其中一次函数的个数是( ) A .1 B .2 C .3 D .4【答案】B 【分析】根据一次函数的定义进行判断即可. 【详解】解:根据一次函数的定义可知:(1)y x =-;(2)1y x =-;是一次函数,(3)1y x=,是反比例函数;(4)2yx ,是二次函数;故一次函数的个数有2个. 故选B .。

一次函数中的动点运动问题一次函数中的动点问题一直是难点。
其难度在于:①直线或点的旋转、平移、翻折运动;②因动直线或动点产生的面积问题;③因动点产生的三角形存在性问题。
解法分析:本题的第1问是点的平移,点的平移运动遵循“上加下减,左减右加”;本题的第2问是直线的左右平移,尽管是新的背景,但是直线的平移就是直线上点的平移运动,只要找准直线上的一个点进行平移运动,代入即可;本题的第3问是点的旋转运动,经过的路径长就是以O为圆心,AO为半径,圆心角为90°的弧长;本题的第4问是直线的旋转运动,只要求出直线上的任意两点(一般选与坐标轴的两交点)绕旋转中心旋转后的对应点,即可求出型的直线表达式。
(旋转后构造“一线三直角模型”,即可求出旋转后对应点的坐标)对于直线的左右平移按照以下方法进行:①从直线上任意取一点进行左右平移,得到平移后的点的坐标;②设出平移后的直线表达式;③将平移后的点代入平移后的表达式中,即可求出b,得到新的表达式。
对于平面直角坐标系中点的旋转运动,往往可以通过构造一线三直角模型,借助全等三角形找到对应的等边。
解法分析:本题的第1问和第2问是手拉手旋转型模型,难度不大,围绕旋转角相等,证明▲AOE'≌▲BOF',即可得到AE'=BF',AE'⊥BF'。
本题的第3问是求P纵坐标的最大值,这是本题的难点,从动态的角度来看,当P与D'重合时,可以求得点P的纵坐标的最大值。
通过画出图形,进行分析,可以得到此时∠A为30°,以此通过30°-60°-90°直角三角形的性质得到点P的纵坐标。
因动点产生的三角形存在性问题有以下几类:①等腰三角形的存在性问题(设点、利用距离公式,线段相等即可求出点的坐标);②直角三角形的存在性问题(设点,利用距离公式和勾股定理求出点的坐标);③等腰直角三角形的存在性问题(根据题意画出图形,利用等腰直角三角形的性质求出点的坐标)。

一次函数动点问题1如图,直线1l 的解析表达式为33y x =-+,且1l 与x 轴交于点D ,直线2l 经过点A B ,,直线1l ,2l 交于点C . (1)求点D 的坐标; (2)求直线2l 的解析表达式; (3)求ADC △的面积;(4)在直线2l 上存在异于点C 的另一点P ,使得ADP △与ADC △的面积相等,请直接..写出点P 的坐标.2.如图,一次函数的函数图象与x 轴、y 轴分别交于点A 、B ,以线段AB 为直角边在第一象限内作Rt △ABC ,且使∠ABC=30°. (1)求△ABC 的面积;(2)如果在第二象限内有一点P (m ,),试用含m 的代数式表示△APB 的面积,并求当△APB 与△ABC 面积相等时m 的值;(3)是否存在使△QAB 是等腰三角形并且在坐标轴上的点Q ?若存在,请写出点Q 所有可能的坐标;若不存在,请说明理由.考点: 一次函数综合题. 专题: 综合题. 分析:(1)先求出A 、B 两点的坐标,再由一个角等于30°,求出AC 的长,从而计算出面积;(2)过P 作PD ⊥x 轴,垂足为D ,先求出梯形ODPB 的面积和△AOB 的面积之和,再减去△APD 的面积,即是△APB 的面积;根据△APB 与△ABC 面积相等,求得m 的值;(3)假设存在点Q,使△QAB是等腰三角形,求出Q点的坐标即可.解答:解:(1)∵一次函数的解析式为函数图象与x轴、y轴分别交于点A、B,∴A(1,0),B(0,),∴AB=2,设AC=x,则BC=2x,由勾股定理得,4x2﹣x2=4,解得x=,S△ABC==;(2)过P作PD⊥x轴,垂足为D,S△APB=S梯形ODPB+S△AOB﹣S△APD==,﹣=,解得m=;(3)∵AB==2,∴当AQ=AB时,点Q1(3,0),Q2(﹣1,0),Q3(0,﹣);当AB=BQ时,点Q4(0,+2),Q2(0,﹣2),Q2(﹣1,0);当AQ=BQ时,点Q6(0,),Q2(﹣1,0),综上可得:(0,),(0,),(﹣1,0)(3,0),(0,),(0,)点评:3.如图,直线1l :8+-=x y 与x 轴、y 轴分别交于点A 和点B ,直线2l :x y =与直线1l 交于点C ,平行于y 轴的直线m 从原点O 出发,以每秒1个单位长度的速度沿x 轴向右平移,到C 点时停止.直线m 交线段BC 、OC 于点D 、E ,以DE 为斜边向左侧作等腰Rt △DEF ,设△DEF 与△BCO 重叠部分的面积为S (平方单位),直线m 的运动时间为t (秒).(1)填空:OA = ,=∠OAB ;(2)填空:动点E 的坐标为(t , ),DE = (用含t 的代数式表示); (3)求S 与t 的函数关系式并写出自变量的取值范围;(4)设直线m 与OA 交于点P ,是否存在这样的点P ,使得P 、O 、F 为顶点的三角形为等腰三角形,若存在,请求出t 的值;若不存在,请说明理由.CB A O xy8:1+-=x y l xy l =:2(备用图1)8:1+-=x y l CP y xmFED OA Bx y l =:24.(10分)如图,一次函数33+=x y 的图象与x 轴、y 轴分别交于A 、B ,以线段AB为直角边在第一象限内作Rt △ABC ,且使∠ABC =30°。
一次函数背景下的动点问题教案【教学目标】1、运用30°直角三角形的三边关系以及菱形的性质、三角形面积公式计算三角形的面积,感受转化思想。
2、在探索△OAE的面积表示的过程中感受分类讨论的思想,学会正确利用数量关系表示面积。
3、在探索面积之间不变关系中提高数学逻辑推理能力及观察能力。
【教学重难点】重点:分类讨论思想的运用。
难点:面积之间不变关系的探索。
一、原题再现x+4与x轴、y轴分别交于A,B两点, C是OB的中如图,直线y=−√33点,D是AB上一点,四边形OEDC是菱形.问:由此你可以得到什么结论?预设:学生可能会得出特殊角的大小、线段长、点的坐标,观到等边三角形,或可以给出三角形的面积等结论。
追问:为什么?预设:学生可能会先由一次函数得出∠OBD=60°,再根据60度角的直角三角形得到线段的长度,及三角形的形状。
设计意图:学生自己观察图形得出结论,不仅熟悉了题目,又发挥了学生的主观能动性,激发学生的学习兴趣。
师可借学生的结论又或是直接展示出原题,给予时间计算。
总结1:求三角形的面积,我们可以通过点E的坐标求得高,通过解直角三角形得到线段长,求出点D的坐标,即可得到点E的坐标。
问1:这里的三角形是怎样一个特殊的三角形?问2:点D、E坐标间有什么关系?总结2:以后碰到函数背景下求面积的问题,我们可以先尝试尝试这条路是否行得通。
设计意图:通过一道题总结出一种方法,不仅为下面的教学作铺垫,更是为学生以后做类似题目时提供思路,抛开题海战术,做到会一题通一类!二、变与不变x+4与x轴、y轴分别交于A,B两点, C是OB的中如图,直线y=−√33点,D是线段AB上一动点,四边形OEDC是平行四边形.(1)已知△OAE的面积为3√3,求点D的坐标。
(2)设点D的横坐标为x,△OAE的面积为S,求S关于x的函数表达式。
(1)预设1:学生上来把两种情况都说出来了。
问:你是怎么想到要分两种情况的?预设2:学生上来只说出了一种情况。
一次函数之动点问题(讲义)一、知识点睛动点问题的特征是速度已知,主要考查运动的过程. 1. 一次函数背景下研究动点问题的思考方向:①把函数信息(坐标或表达式)转化为基本图形的信息; ②分析运动过程,注意状态转折,确定对应的时间范围; ③画出符合题意的图形,研究几何特征,设计解决方案. 2. 解决具体问题时会涉及线段长的表达,需要注意两点:①路程即线段长,可根据s =vt 直接表达已走路程或未走路程;②根据研究几何特征需求进行表达,既要利用动点的运动情况,又要结合基本图形信息.二、精讲精练1. 如图,在平面直角坐标系中,O 为坐标原点,直线334y x =-+与x 轴、y 轴分别交于A ,B 两点.点P 从点A 出发,以每秒1个单位的速度沿射线AO 匀速运动,设点P 的运动时间为 t 秒.(1)求OA ,OB 的长.(2)过点P 与直线AB 垂直的直线与y 轴交于点E ,在点P 的运动过程中,是否存在这样的点P ,使△EOP ≌△AOB ?若存在,请求出t 的值;若不存在,请说明理由.y xOBA2. 如图,直线=3+43y x 与x 轴、y 轴分别交于A ,B 两点,直线BC 与x 轴交于点C ,∠ABC =60°.(1)求直线BC 的解析式.(2)若动点P 从点A 出发沿AC 方向向点C 运动(点P 不与点A ,C 重合),同时动点Q 从点C 出发沿折线CB —BA 向点A 运动(点Q 不与点A ,C 重合),动点P 的运动速度是每秒1个单位长度,动点Q 的运动速度是每秒2个单位长度.设△APQ 的面积为S ,运动时间为t 秒,求S 与t 之间的函数关系式,并写出自变量t 的取值范围. (3)当t =4时,y 轴上是否存在一点M ,使得以A ,Q ,M 为顶点的三角形为等腰三角形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.C ABOxy CABOxy3. 如图,在直角梯形COAB 中,OC ∥AB ,以O 为原点建立平面直角坐标系,A ,B ,C三点的坐标分别为A (8,0),B (8,11),C (0,5),点D 为线段BC 的中点.动点P 从点O 出发,以每秒1个单位的速度,沿折线OA —AB —BD 的路线运动,至点D 停止,设运动时间为t 秒.(1)求直线BC 的解析式.(2)若动点P 在线段OA 上运动,当t 为何值时,四边形OPDC 的面积是梯形COAB 面积的14?(3)在动点P 的运动过程中,设△OPD 的面积为S ,求S 与t 之间的函数关系式,并写出自变量t 的取值范围.P DCxA OByyBO A xCD4. 如图,直线334y x =-+与x 轴交于点A ,与直线33y x =交于点P . (1)求点P 的坐标. (2)求△OP A 的面积.(3)动点E 从原点O 出发,以每秒1个单位的速度沿OA 方向向终点A 运动,过点E 作EF ⊥x 轴交线段OP 或线段P A 于点F ,FB ⊥y 轴于点B .设运动时间为t 秒,矩形OEFB 与△OP A 重叠部分的面积为S ,求S 与t 之间的函数关系式.PFE xA OB y5. 如图,直线l 的解析式为y =-x +4,它与x 轴、y 轴分别交于A ,B 两点,平行于直线l的直线m 从原点O 出发,沿x 轴的正方向以每秒1个单位长度的速度运动,它与x 轴、y 轴分别交于M ,N 两点,设运动时间为t 秒(0< t <4). (1)求A ,B 两点的坐标;(2)用含t 的代数式表示△MON 的面积S 1;(3)以MN 为对角线作矩形OMPN ,记△MPN 和△OAB 重 叠部分的面积为S 2,试探究S 2与t 之间的函数关系式.xy OABm l PM N【参考答案】1.(1)OA =4,OB =3; (2)t =1或t =7 2.(1)343y x =-+(2)223(04)2343(48)2t t S t t t ⎧<⎪⎪=⎨⎪-+<<⎪⎩≤(3)123(0438)(0438)(043)M M M -+-,或,或,443(0)3M 或,3.(1)354y x =+(2)32t =(3)4(08)248(819)248(1924)t t S t t t t <⎧⎪=-+<⎨⎪-+<<⎩≤≤4.(1)(33)P , (2)23(3)223(03)653163243(34)2tt S t t t ⎧<⎪⎪=⎨⎪-+-<<⎪⎩≤5.(1)(40)(04)A B ,,,(2)2112S t =(3)2221(02)2388(24)2t t S t t t ⎧<⎪⎪=⎨⎪-+-<<⎪⎩≤。
一次函数动点问题(一)1.一次函数y=ax+b (a 为整数)的图象过点(98,19),交x 轴于(p,0),交y 轴于(0,q ),若p 为质数,q 为正整数,那么满足条件的一次函数的个数为_________个。
2.过点P(-1,3)作直线,使它与两坐标轴围成的三角形面积为5,这样的直线可以作_______条 3、一次函数y=ax+b ,若a+b=1,则它的图象必经过点_______________7.当-1≤x ≤2时,函数6+=ax y 满足10<y ,则常数a 的取值范围是_________________4.在直角坐标系中,横坐标都是整数的点称为整点,设k 为整数,当直线y=x -3与y=kx+k 的交点为整数时,k的值可以取_____________5.函数的自变量x 的取值范围是_____。
6.已知:不论k 取什么实数,关于x 的方程1632=--+bkx a kx (a 、b 是常数)的根总是x =1,试求a 、b 的值。
7.如图,在一次函数3+-=x y 的图象上取点P ,作PA ⊥x 轴,PB ⊥y 轴;垂足为B ,且矩形OAPB 的面积为2,则这样的点P 共有多少个?8、在平面直角坐标系中,有A (0,5),B (5,0),C (0,3),D (3,0)且AD 与BC 相交于点E 求△ABE 的面积9、一个一次函数的图象与直线59544y x =+平行,与x 轴、y 轴的交点分别为A 、B ,并且经过点(-1,-25),则线段AB 上(包括端点A 、B )横、纵坐标都是整数的点有________________10、如图,直线313y x =-+与x 轴、y 轴分别交于A 、B ,以线段AB 为直角边在第一象限内作等腰Rt ΔABC ,∠BAC=90° ,如果在第二象限内有一点P (a ,12),且ΔABP 的面积与ΔABC 的面积相等,求a 的值 yxA OB PyxPO B A11、如图,直线L :221+-=x y 与x 轴、y 轴分别交于A 、B 两点,在y 轴上有一点C (0,4),动点M 从A 点以每秒1个单位的速度沿x 轴向左移动。
【关键字】教师一次函数动点问题一、选择与填空1.如图1,点A的坐标为(1,0),点B在直线上运动,当线段AB最短时,点B的坐标为A.(0,0)B.(,-)C.(,-)D.(-,)2. 如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是()A.3 B.4 C.5 D.63.如图,点G、D、C在直线a上,点E、F、A、B在直线b上,若从如图所示的位置出发,沿直线b向右匀速运动,直到EG与BC重合.运动过程中与矩形重合部分的面积(S)随时间(t)变化的图象大致是()4.如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度大小不变,则以点A为圆心,线段AP长为半径的圆的面积S与点P的运动时间t之间的函数图象大致为()二、存在性问题1.如图,以等边△OAB的边OB所在直线为x轴,点O为坐标原点,使点A在第一象限建立平面直角坐标系,其中△OAB边长为6个单位,点P从O点出发沿折线OAB向B点以3单位/秒的速度向B点运动,点Q 从O点出发以2单位/秒的速度沿折线OBA向A点运动,两点同时出发,运动时间为t(单位:秒),当两点相遇时运动停止.①点A坐标为_____________,P、Q两点相遇时交点的坐标为________________;②当t=2时,____________;当t=3时,____________;③设△OPQ的面积为S,试求S关于t的函数关系式;④当△OPQ的面积最大时,试求在y轴上能否找一点M,使得以M、P、Q为顶点的三角形是Rt△,若能找到请求出M点的坐标,若不能找到请简单说明理由。
2.如图①,过点(1,5)和(4,2)两点的直线分别与x轴、y轴交于A、B两点.(1)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.图中阴影部分(不包括边界)所含格点的个数有_________个(请直接写出结果);(2)设点C(4,0),点C关于直线AB的对称点为D,请直接写出点D的坐标_________;(3)如图②,请在直线AB和y轴上分别找一点M、N使△CMN的周长最短,在图②中作出图形,并求出点N的坐标.考点:一次函数综合题。
分析:(1)先利用待定系数法求得直线AB的解析式为y=﹣x+6;再分别把x=2、3、4、5代入,求出对应的纵坐标,从而得到图中阴影部分(不包括边界)所含格点的坐标;(2)首先根据直线AB的解析式可知△OAB是等腰直角三角形,然后根据轴对称的性质即可求出点D 的坐标;(3)作出点C关于直线y轴的对称点E,连接DE交AB于点M,交y轴于点N,则此时△CMN的周长最短.由D、E两点的坐标利用待定系数法求出直线DE的解析式,再根据y轴上点的坐标特征,即可求出点N的坐标.解答:解:(1)设直线AB的解析式为y=kx+b,把(1,5),(4,2)代入得,kx+b=5,4k+b=2,解得k=﹣1,b=6,∴直线AB 的解析式为y=﹣x+6; 当x=2,y=4; 当x=3,y=3; 当x=4,y=2; 当x=5,y=1.∴图中阴影部分(不包括边界)所含格点的有: (1,1),(1,2),(1,3),(1,4), (2,1),(2,2),(2,3), (3,1),(3,2), (4,1). 一共10个;(2)∵直线y=﹣x+6与x 轴、y 轴交于A 、B 两点, ∴A 点坐标为(6,0),B 点坐标为(0,6), ∴OA=OB=6,∠OAB=45°.∵点C 关于直线AB 的对称点为D ,点C (4,0), ∴AD=AC=2,AB ⊥CD , ∴∠DAB=∠CAB=45°, ∴∠DAC=90°,∴点D 的坐标为(6,2);(3)作出点C 关于直线y 轴的对称点E ,连接DE 交AB 于点M ,交y 轴于点N ,则NC=NE ,点E (﹣4,0).又∵点C 关于直线AB 的对称点为D ,∴CM=DM ,∴△CMN 的周长=CM+MN+NC=DM+MN+NE=DE ,此时周长最短. 设直线DE 的解析式为y=mx+n . 把D (6,2),E (﹣4,0)代入,得 6m+n=2,﹣4m+n=0, 解得m=,n=,∴直线DE 的解析式为y=x+. 令x=0,得y=,∴点N 的坐标为(0,). 故答案为10;(6,2).3.如图,在平面直角坐标系xOy 中,直线1y x =+与334y x =-+交于点A ,分别交x 轴于点B 和点C ,点D 是直线AC 上的一个动点.(1)求点A B C ,,的坐标.(2)当CBD △为等腰三角形时,求点D 的坐标. (3)在直线AB 上是否存在点E ,使得以点E D O A ,,,为顶点的四边形是平行四边形?4.如图,四边形OABC 为直角梯形,BC ∥OA ,A (9,0),C (0,4),AB=5 点M 从点O 出发以每秒2个单位长度的速度向点A 运动;点N 从点B 同时出发,以每秒1个单位长度的速度向点C 运动.其中一个动点到达终点时,另一个动点也随之停止运动. (1)求直线AB 的解析式;(2)t 为何值时,直线MN 将梯形OABC 的面积分成1:2两部分;A y x DC OB(3)当t=1时,连接AC、MN交于点P,在平面内是否存在点Q,使得以点N、P、A、Q为顶点的四边形是平行四边形?如果存在,直接写出点Q的坐标;如果不存在,请说明理由.考点:一次函数综合题。
分析:(1)作BD⊥OA于点D,利用勾股定理求出AD的值,从而求出B点的坐标,利用待定系数法求出直线AB的解析式;(2)梯形面积分为1:2的两部分,要注意分两种去情况进行分别计算,利用面积比建立等量关系求出t的值.(3)M、N两点的坐标求出MN的解析式和AC的解析式,利用直线与方程组的关系求出P点坐标,利用三角形全等求出Q、Q1的坐标,求出直线Q1P、QN的解析式,再求出其交点坐标就是Q2的坐标.解答:解:(1)作BD⊥0A于点D.∴BD=4,∵AB=5,由勾股定理得AD=3∴OD=6∴B(6,4)设直线AB的解析式为:y=kx+b,由题意得解得:∴直线AB的解析式为:;(2)设t秒后直线MN将梯形OABC的面积分成1:2两部分,则BN=t,CN=6﹣t,OM=2t,MA=9﹣2t当S四边形OMNC:S四边形NMAB=1:2时解得:t=﹣1(舍去)当S四边形OMNC:S四边形NMAB=2:1时,解得t=4∴t=4时,直线MN将梯形OABC的面积分成1:2两部分.(3)存在满足条件的Q点,如图:Q(9.5,2),Q1(8.5,﹣2),Q2(0.5,6).点评:本题是一道一次函数的综合试题,考查了用待定系数法求函数的解析式,图形的面积,直线的解析式与二元一次方程组的关系,勾股定理及三角形全等的性质的运用.5.在平面直角坐标系中,△AOC中,∠ACO=90°.把AO绕O点顺时针旋转90°得OB,连接AB,作BD ⊥直线CO于D,点A的坐标为(﹣3,1).(1)求直线AB的解析式;(2)若AB中点为M,连接CM,动点P、Q分别从C点出发,点P沿射线CM以每秒个单位长度的速度运动,点Q沿线段CD以每秒1个长度的速度向终点D运动,当Q点运动到D点时,P、Q同时停止,设△PQO的面积为S(S≠0),运动时间为T秒,求S与T的函数关系式,并直接写出自变量T的取值范围;(3)在(2)的条件下,动点P在运动过程中,是否存在P点,使四边形以P、O、B、N(N为平面上一点)为顶点的矩形?若存在,求出T的值.考点:一次函数综合题。
分析:(1)先求出点B的坐标,再代入一次函数的解析式即可;(2)根据AB中点为M,求出点M的坐标,再求出CM的解析式,过点P做PH⊥CO交CO于点H,用t表示出OQ和PH的长,根据S=OQ•PH即可求出S与T的函数关系式;(3)此题需分四种情况分别求出T 的值即可. 解答:解:(1)∵∠AOB=90°, ∴∠AOC+∠BOC=90°∵BD 垂直于CD ∵∠BDO=90°,∠OBD+∠BOD=90°, ∠AOC=∠BOD ,∵OA=OB ∠AOC=∠BOD=90°, ∴△AOC ≌△OBD , ∴AC=OD ,CO=BD ∵A (﹣3,1),∴AC=OC=1,OC=BD=3, ∴B (1,3), ∴y=x+;(2)M (﹣1,2),C (﹣3,0), ∴直线MC 的解析式为:y=x+3 ∴∠MCO=45°,过点P 做PH ⊥CO 交CO 于点H ,S=OQ•PH=(3﹣t )×t=t 2+t (0<t <3) 或S=(t ﹣3)t=t 2﹣t (3<t≤4); (3)t 1=,t 2=,t 3=,t 4=2.点评:此题考查了一次函数的综合应用,解题时要注意分类讨论,关键是能用t 表示出线段的长度求出解析式.三、计算问题1.如图,直线1l 的解析表达式为33y x =-+,且1l 与x 轴交于点D ,直线2l 经过点A B ,,直线1l ,2l 交于点C .(1)求直线2l 的解析表达式; (2)求ADC △的面积;(3)在直线2l 上存在异于点C 的另一点P ,使得ADP △与ADC △的面积相等,请直接..写出点P 的坐标.(4)若点H 为坐标平面内任意一点,在坐标平面内是否存在这样的点H ,使以A 、D 、C 、H 为顶点的四边形是平行四边形?若存在,请直接写出点H 的坐标;若不存在,请说明理由.考点:一次函数综合题。
专题:综合题。
分析:(1)结合图形可知点B 和点A 在坐标,故设l 2的解析式为y=kx+b ,由图联立方程组求出k ,b 的值;(2)已知l 1的解析式,令y=0求出x 的值即可得出点D 在坐标;联立两直线方程组,求出交点C 的坐标,进而可求出S △ADC ;(3)△ADP 与△ADC 底边都是AD ,面积相等所以高相等,ADC 高就是C 到AD 的距离;(4)存在;根据平行四边形的性质,可知一定存在4个这样的点,规律为H 、C 坐标之和等于A 、D 坐标之和,设出代入即可得出H 的坐标.解答:解:(1)设直线l2的解析表达式为y=kx+b,由图象知:x=4,y=0;x=3,,∴,∴,∴直线l2的解析表达式为;(2)由y=﹣3x+3,令y=0,得﹣3x+3=0,∴x=1,∴D(1,0);由,解得,∴C(2,﹣3),∵AD=3,∴S△ADC=×3×|﹣3|=;(3)△ADP与△ADC底边都是AD,面积相等所以高相等,ADC高就是C到AD的距离,即C纵坐标的绝对值=|﹣3|=3,则P到AB距离=3,∴P纵坐标的绝对值=3,点P不是点C,∴点P纵坐标是3,∵y=1.5x﹣6,y=3,∴1.5x﹣6=3x=6,所以点P的坐标为(6,3);(4)存在;(3,3)(5,﹣3)(﹣1,﹣3)点评:本题考查的是一次函数的性质,三角形面积的计算以及平行四边形的性质等等有关知识,有一定的综合性,难度中等偏上.2.如图,在Rt△AOB中,∠AOB=90°,OA=3cm,OB=4cm,以点O为坐标原点建立坐标系,设P、Q分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)(1)过点P做PM⊥OA于M,求证:AM:AO=PM:BO=AP:AB,并求出P点的坐标(用t表示)(2)求△OPQ面积S(cm2),与运动时间t(秒)之间的函数关系式,当t为何值时,S有最大值?最大是多少?(3)当t为何值时,△OPQ为直角三角形?(4)证明无论t为何值时,△OPQ都不可能为正三角形。