平面曲线的曲率

平面曲线的曲率第一部分：教案（P1-6）第二部分：说课稿（P7-11）2009年12月《平面曲线的曲率》教案课题：平面曲线的曲率课时：2课时（90分钟）教学目标：认知目标：1、理解曲率的概念和曲率公式的实际应用；2、了解曲率圆和曲率半径的概念；3、掌握曲率计算公式的推导过程及公式的实际应用，真正体会微积分和导数在数学中的重要地位。

能力目标：激发学生的数学学习兴趣，加强数学建模的能力，掌握归纳总结的数学思想方法，培养学生联系实际学习的意识，增进数学应用的眼光，提高学生的主观能动性情感目标：培养学生勇于探索、大胆应用的数学精神，培养团结协作的意识。

教学重点：曲率的概念，曲率计算公式的实际应用。

教学难点：利用曲率计算公式解决实际应用问题。

教学方法：引导探究法（Enlightment）、分层次教学法（Delamination）、任务驱动法（Assignment）。

教学工具：木杆、多媒体课件教学。

教学过程：一、引入：前面我们已经学习了导数的应用，例如函数极值、最值的求解，函数单调性的判断及函数图像的描绘等，我们体会了导数的重要性，曾有人说微积分和导数是最伟大的人类心智成就之一，足以可见它们在人类生产生活中的应用之广泛，今天我们要继续学习导数的另一个应用——“平面曲线的曲率”，这个内容虽然是个选修内容，可是对于我们工程机械专业的学生来说是个不得不学的内容，所以我们接下来就来探讨有关平面曲线的曲率的问题。

二、新课讲解：（一）引入课题：（5分钟）操作实验，并布置任务。

感性认识“直”——“弯”——“最弯之处”：取一根笔直的木杆，当它放置于桌面上时，它很明显时直的，没有弯曲。

当它的两端各受另一个向上的外力时，它马上会开始弯曲，在这个过程中，有的地方弯曲程度大，有的地方弯曲程度小，随着力度的增大，竹片会断裂，很明显我们可以得出结论：断裂处就是弯曲得最厉害的地方。

当然弯曲的时木杆，断裂了也没什么关系，但若是因荷载作用而弯曲变形的船体结构中的钢梁，我们是不能让它们断裂的，所以我们必须找到那个最容易断裂的地方，然后给它加固，或者我们要采取一些什么样的措施来防止因为弯曲而容易断裂的铁路铁轨的问题呢？在数学领域里，我们用曲率来描述曲线的弯曲程度，因此今天我们就来探讨“平面曲线的曲率”的问题。

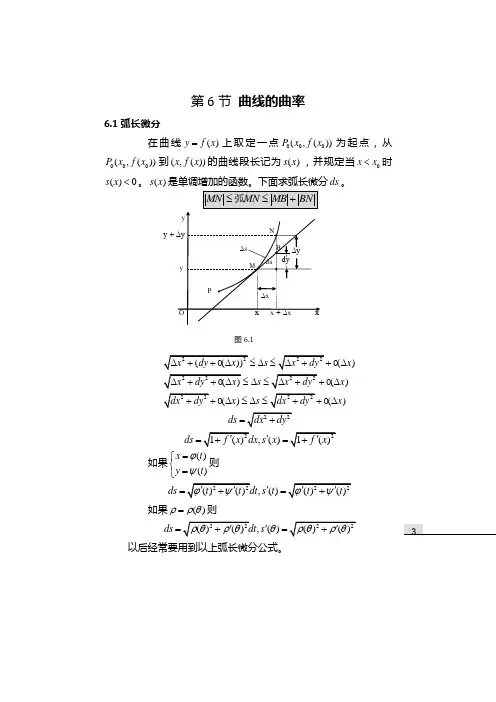
第6节 曲线的曲率6.1弧长微分在曲线()y f x =上取定一点000(,())P x f x 为起点，从000(,())P x f x 到(,())x f x 的曲线段长记为()s x ，并规定当0x x <时()0s x <。

()s x 是单调增加的函数。

下面求弧长微分ds 。

()()()()s x s x x s x ≤∆≤∆≤∆≤∆∆≤∆≤∆ds =,()ds s x '== 如果()()xt y t ϕψ=⎧⎨=⎩则,()ds s t '==如果()ρρθ=则,()ds s θ'==以后经常要用到以上弧长微分公式。

图6.1y +离 散数 学6.2曲线的曲率这节讨论曲线的曲率，也就是曲线的弯曲程度。

设曲线()y f x =在()00,()x f x 的切线0L 与x 轴正向的夹角为0θ，在()00,()x x f x x +∆+∆的切线x L ∆与x 轴正向的夹角为x θ∆。

经过x ∆，切线的夹角变化了0x θθθ∆∆=-设()00,()x f x 和()00,()x x f x x +∆+∆之间曲线的长为s ∆。

容易想见，()00,()x f x 和()00,()x x f x x +∆+∆之间曲线的曲率（弯曲程度）与θ∆成正比，与s ∆成反比，平均曲率()k x sθ∆∆=∆ 让0x ∆→求极限，就得到曲线()y f x =在()00,()x f x 的曲率（弯曲程度）000()lim ()limx x d k x k x s dsθθ∆→∆→∆=∆==∆ 下面我们求出d dsθ从而得到求曲率的计算公式。

用x 作参数 ()()s s x x θθ=⎧⎨=⎩()()2222tan ()1()cos 1tan ()1()()()1()f x d f x dx d f x dx f x d f x dxd f x dx f x θθθθθθθ'=''=''+='''+=''='+第1章集 合322()1()d f x d ds dxdxds f x θθ''=='⎡⎤+⎣⎦003220()()1()f x k x f x ''='⎡⎤+⎣⎦例子：求半径为r 的圆上一点的曲率。

平面解析几何基础知识曲线的曲率与半径在平面解析几何中，曲线的曲率和曲线的半径是非常重要的基础知识。

曲线的曲率描述了曲线在某一点处弯曲的程度，而曲线的半径则是曲线在该点处的弯曲半径。

一、曲率的定义和计算方法曲线在某一点处的曲率是该点处曲线切线的变化率。

设曲线方程为y=f(x)，则曲线在点(x0,y0)处的曲率K可以通过以下公式计算：K=|y''|/(1+y'²)^(3/2)，其中y'和y''分别表示曲线方程的一阶和二阶导数。

二、曲率的几何意义曲线的曲率可以反映曲线的弯曲程度。

当曲率K为正时，曲线向外凸出，表示曲线在该点处向外弯曲；当曲率K为负时，曲线向内凹陷，表示曲线在该点处向内弯曲；当曲率K为零时，曲线是直线。

曲率的绝对值越大，曲线在该点处的弯曲程度越大。

三、曲线的半径和曲率的关系曲线在某一点处的曲率K与曲线的半径R满足如下关系：K=1/R。

即曲线的曲率等于曲线的半径的倒数。

这意味着曲线的半径越大，曲线的曲率越小，曲线的弯曲程度越小；曲线的半径越小，曲线的曲率越大，曲线的弯曲程度越大。

四、曲线的曲率与切线方向的关系曲线在某一点处的曲率K与曲线在该点处的切线方向有密切关系。

当曲率K为正时，曲线的切线方向是逆时针旋转的；当曲率K为负时，曲线的切线方向是顺时针旋转的。

五、曲线的曲率和半径的应用曲线的曲率和半径在计算机图形学、物理学、工程学等领域有广泛的应用。

在计算机图形学中，曲线的曲率和半径常用于绘制平滑的曲线和曲面，以及进行形状分析；在物理学中，曲线的曲率和半径用于描述粒子在运动过程中的轨迹；在工程学中，曲线的曲率和半径用于设计道路的弯曲程度和转弯半径。

综上所述，曲线的曲率和曲线的半径是平面解析几何中的基础知识。

它们描述了曲线在某一点处的弯曲程度和弯曲半径，对于理解和分析曲线的性质和特点非常重要。

这些知识在实际应用中有广泛的用途，能够帮助我们解决各种问题，并且在科学研究和工程设计中起着重要的作用。

在微分几何中，曲率的倒数就是曲率半径，即R=1/K。

平面曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率，通过微分来定义，表明曲线偏离直线的程度。

拐点则是曲线上一个特殊的点，在该点处，曲线的曲率发生变化，即函数的二阶导数在该点处为零或不存在。

在拐点处，曲线的凹凸性也会发生变化。

曲率半径和拐点都是描述曲线性质的重要概念。

曲率半径主要用来描述曲线上某处曲线弯曲变化的程度，而拐点则是曲线上一个特殊的点，在该点处曲线的性质会发生变化。

以上内容仅供参考，如需更详细的分析，可查阅数学书籍或咨询数学专业人士。

平面曲线的相对曲率公式的几种证明方法
在上个世纪，许多著名的几何家试图证明,平面曲线的相对曲率公式——弗里斯特公式（Fresnel Formula），使用三种不同的方法: 牛顿-古典，几何统计，和古典分析。

这些证明方法在证明这个公式时，具有独特的一面。

本文将介绍牛顿-古典，几何统计，和古典分析三种不同的证明方法。

牛顿-古典证明方法是最古老的一种，由著名的科学家牛顿发展。

在这种定义方法中，弗里斯特公式被视为一种牛顿力的函数，即在曲线的拐角处，力的改变和曲线的曲率之间存在关系。

几何统计方法是由克里穆奇数学家于一九九三年提出的，他认为，当曲线是连续不变的时候，它的相对曲率也应该是连续不变的，而不是分开考虑。

因此，这种方法把曲线抽象为曲线的统计运动，旋转曲线，和不断细分曲线。

它们通过把曲线上的点作为独立的抽象元素，用坐标表示曲线，并用克里穆厄方程计算出曲率的函数。

最后，古典分析方法使用一种简单的数学模型来表达曲线的相对曲率，模型通过分析曲线上各类特有点来确定特定曲率，然后根据曲率推导出曲率的函数。

若曲线的问题如果可以改变弯曲角度，古典分析方法就可以计算出曲率的更精确的表达式。

通过以上三种定义方法，弗里斯特公式可以得到正确的结果，它有助于我们更深入理解平面曲线，并利用它们的特性来制作不同的产品和实现各种美学的形状。

知识点：平面曲线的曲率（MC20306） 1 背景知识与引入方法在微分几何学中,与平面曲线有关的是三个基本概念：长度、切线和曲率. 瑞士数学家L ⋅欧拉在1736年首先引进了平面曲线内在坐标这一概念.从而开始了曲线内在几何的研究.欧拉将曲率描述为曲线的切线方向和一固定方向的交角相对于弧长的变化率,这也成为一些教材引入曲率概念的方法之一.1847年弗雷内得出了曲线的基本微分方程,亦即统称弗雷内公式.后来,G ⋅达布创造了空间曲线的活动标架概念,完整地建立起曲线理论.所以有些教材把空间的弗雷内标架改造为平面弗雷内公式而导出带有正负号平面曲线曲率公式，它既表示曲线的弯曲程度，又表示曲线的弯曲方向.（如：萧树铁、居余马主编的《高等数学》第Ⅲ卷,或马知恩、王锦森主编的《工科数学分析基础》）.大多教材通常在直角坐标系下,在曲线上相邻两点的切向量()t s 和()t s s +∆之间夹角α∆关于弧长s ∆的变化率||lim 0ss ∆∆→∆α引出曲率公式. 由实际问题先引出曲率圆、曲率半径概念,由曲率半径概念自然给出曲率定义,我们认为方法简洁省事（如章栋恩等人编写《高等数学》上册）.2 该知识点讲解方法2.1讲解方法一：曲率是一个构造型的定义,通常由解决某一具体实际问题的方法来讲清其构造的道理,再引出曲率概念其教法更为简捷,例如力学问题中质点做曲线运动,在某点局部情形的研究,可用圆周曲线来代替,而此圆周曲线（曲率圆）的建立仅仅使用了一阶导、二阶导的简单应用,却以最好的方式接近已知曲线,进而引出了曲率半径定义.2.1.1曲率圆1、实际问题： 一质点作曲线运动,考察此运动在某点))(,(00x f x M 局部情形时,可用圆周曲线来替代这点附近的曲线L,这样就可以用圆周运动的知识来分析这点处的曲线运动.（问题：什么样的圆周曲线在点M 更接近曲线L 呢？）2、试求一个圆周曲线C ： 222()()x y αβρ-+-= （1） 使之满足C 过点))(,(00x f x M ： 22200()()x y αβρ-+-= （2） C 与L 在点M 有相同斜率： )(000x f y y y x x '='== （3）C 与L 在点M 有相同凹性： 0000≠''=''==)(x f y y y x x （4）（1）式两边对x 求二阶导： 0)(2)(2='-+-y y x βα0)(2)(222=''-+'+y y y β（3）（4）式代入上面两式有：0)(])([)(000='-+-x f x f x βα （5） 0)(])([)]([10020=''-+'+x f x f x f β （6）从（6）式解出： )()]([1)(0200x f x f x f '''++=β 将其代入（5）式解出200001[()]()()f x x f x f x α'+'=-'' βα,代入（2）式解出：|)(|])(1[02/320x f x f '''+=ρ. 3、定义： 曲线L 即 )(x f y =上的点)(,(00x f x M 处，在其凹向一侧的法线上取一点),(βαD 为圆心,以)()]([023021x f x f MD '''+==ρ为半径所得到的圆为L 在点M 处的曲率圆,ρ为曲率半径.2.1.2曲率1、曲率就是曲线在某点处的弯曲程度.如路弯度大,车子离心率越大；梁一般在弯的最厉害的地方断裂；……圆的半径越小弯的越厉害,于是2、定义：23020)](1[)(1x f x f k '+''==ρ为曲线)(x f y =在点))(,(00x f x 处曲率.2.2讲解方法二：通常与分析曲线弯曲程度与曲线上相邻两点的切向量()t s 和()t s s +∆之间的夹角α∆大小有关,当转角相同时,又与弧段的长短有关,于是曲率由α∆关于s ∆的变化率0lim s sα∆→∆∆来叙述.2.2.1弧微分 （这里只介绍弧微分公式的初等几何解释）设函数()f x 在区间(,)a b 内具有连续导数.基点为00(,)A x y ,(,)M x y 为曲线上任意点,规定：（1） 曲线的正向与x 增大的方向一致； （2） 有向弧段AM 的值表为：s AM =；当AM 的方向与曲线的正向一致时, s 取正号；相反时, s 取负号.设弧MN 是从点(,)M x y 起弧长的改变量s ∆，而x ∆和y ∆是相应的y x 和的改变量，由直角三角形得到：,)()()(222y x MN ∆+∆=由此，,)(1)()(222xy x MN ∆∆+=∆ 当0x ∆→时，假定这条曲线具有连续导数，可用弧长代替,MN 再对0x ∆→时取极限，得到22)d d (1)d d (xy x s +=由此得到弧长微分表达式x y s d 1d 2'+±=或22)d ()d (d y x s +±=如果弧长是朝增加的方向变化的，则s d 取正号，反之取负号.2.2.2曲率及其计算公式1、曲率的定义1、曲率是描述曲线局部性质（弯曲程度）的量. 设曲线C是光滑的,0M 是基点.Δs ='M M ,'M M →切线转角为α∆.定义：弧段M M '的平均曲率为sK ∆∆=α,曲线C 在点M 处的曲率0lims K sα∆→∆=∆. 在0lims d s dsαα∆→∆=∆存在的条件下,s K d d α=.注 意：（1）直线的曲率处处为零；（2）圆上各点处的曲率等于半径的倒数,且半径越小曲率越大.2、曲率的计算公式 （ⅰ）设()y f x =二阶可导,tan 'y α=,有arctan 'y α=,dx 1d 2y y '+''=α, x y d 1ds 2'+=,232)1(y y k '+''=∴.（ⅱ）设⎩⎨⎧==)()(t y t x ψϕ,二阶可导,)()(d d t t s y ϕψ''= , )()()()()(d d 322t t t t t x y ϕψϕψϕ''''-'''=， 3222()()()().[()()]t t t t k t t ϕψϕψϕψ''''''-∴=''+2.2.3 曲率圆与曲率半径定义：设曲线()y f x =在点(,)M x y 处的曲率为(0)k k ≠.在点M 处的曲线的法线上,在凹的一侧取一点D,使1DM kρ==.以D 为圆心,ρ为半径作图（如图）,称此圆为曲线在点M 处的曲率圆.D —曲率中心, ρ—曲率半径注意：1、线上一点处的曲率半径与曲线在该点处的曲率互为倒数.即1kρ=,1k ρ=.2、曲线上一点处的曲率半径越大,曲线在该点处的曲率越小（曲线越平坦）；曲率半径越小,曲率越大（曲线越弯曲）.3、一点处的曲率圆弧可近似代替该点附近曲线弧（称为曲线在该点附近的二次近似）.2.3 讲解方法三用曲线离开切线的速度刻画曲率；在已知弧长积分表达式的前提下推导曲率计算公式. 2.3.1曲率：曲率是表示曲线方向改变快慢的量.设A 是曲线L 上点,M 是接近A 的点(图1).由A 沿曲线到M 其切线的转角为ϕ,长度s ∆的弧段AM 的平均旋转速度k sϕ=∆.定义曲线L 在点A 处曲率lims k sϕ∆→=∆.例：讨论圆的曲率（图2） 角ϕ所张的弧AM 长度s r ϕ∆=,于是1s rϕ=∆, 所以圆所有点处的曲率都相同，等于半径的倒量.2.3.2曲率公式：平面曲线L 由函数()y f x =给出,具有连续导数，取固定点N 作为计算弧长的起点（图3）,切线倾斜角从点A 到M 的改变量ϕα=∆，s xs x s sk x s s ''=∆∆∆∆=∆∆=∆=→∆→∆→∆||lim limlim00αααϕ， 其中⎰'+=xa x x y s d )(12,y '=αtan ,故y '=arctan α，得21y y '+''='α.最终有232)1(y y k '+''= .2.4讲解方法四：曲线的解析表达式以矢量形式给出,在已有矢函数微分积分知识的前提下给出曲率概念.给定曲线：()r r t =,（t αβ≤≤）,图3 图 2图 1弧长()s t ：⎰'=βαt t r t s d )()(,r s d d =是弧微分.单位切矢：)()(t r t r τ''= ，则n k sτ=d d .n 是曲线的单位法矢.这样s τk d d=是曲率,1R k =是曲率半径, 以n R r +为矢径的点是曲率中心.具体形式，若j t y i t x r )()(+=, 则2322])()([)()()()(t y t x t y t x t y t x k +''''-'''=. 若j y i x r+=, 则232''(1')y k y =+.例题的选择方法：曲率的实际应用,根据专业特点选择为好.3 例题例1 直线的曲率恒为零.解：直线b ax y +=,因0=''y ,故各点处曲率为零,所以直线不弯. 例2 抛物线c bx ax y ++=2上哪点曲率最大？ 解：由于b ax y +='2,a y 2='',故3222[1(2)]a k axb =++,当02=+b ax ,即2bx a=-时,k 取最大值a 2, 故抛物线c bx ax y ++=2在顶点处),(ab ac a b 4422--处曲率最大. 例3 一工件内表面截线为24.0x y =,用砂轮磨削其内表面,半径多大合适？ 解：砂轮半径≤抛物线上各点处曲率半径的最小者,才不会破坏工件内表面,由例2知抛物线在顶点处曲率最大,曲率半径最小.x y 8.0=',8.0=''y ,320.8(0,0)0.8(10)k ==+,25.11==kρ,所以砂轮半径不能大于1.25．4 扩展知识黎曼流形的曲率是微分几何中最重要的几何量之一，曲率和流形的拓扑结构之间的联系是一个十分重要的问题．对于黎曼流形来说,有三种不同层次的曲率,一种是截面曲率,它相应于在每点某一平面方向所相应的曲率.另一种是里奇曲率,它是由截面曲率以适当的形式作和而成.第三种是数量曲率,它是里奇曲率的迹.这三种曲率和流形的拓扑性质之间有很强的相互制约作用,这方面的研究成果非常丰富,而且是微分几何主要研究方向之一．5 参考文献[1] 章栋恩，金元怀．高等数学．北京：中国标准出版社，1998[2] 同济大学应用数学系．高等数学．北京：高等教育出版社，2002[3] A.Д.亚历山大洛夫．数学——它的内容、方法和意义．北京：科学技术出版社，19596 参考教案MC20306.ppt。