平面曲线的弧长与曲率
- 格式:doc
- 大小:215.50 KB
- 文档页数:4

弧线的长度和曲率的关系及其在物理学中的应用弧线是曲线的一种特殊形式,它具有一定的长度和曲率。
本文将探讨弧线的长度和曲率之间的关系,并介绍在物理学中这种关系的应用。
一、弧线的长度和曲率的概念弧线是指在平面上不同点之间的连续曲线。
弧线的长度是指这条曲线所覆盖的实际距离。
曲率是指在曲线上某一点处的切线与该点附近曲线的弯曲程度,曲率的大小与曲线的弯曲程度成正比,可以用弧长来表示。
二、弧线的长度和曲率之间的关系在微积分中,弧长可以通过积分来计算。
设曲线方程为y=f(x),x从a到b,弧线的长度可以表示为:L = ∫[a,b] √(1+(dy/dx)^2) dx其中,dy/dx为曲线斜率的导数。
而曲率可以通过求导数来计算,即:k = |dy/dx| / (1+(dy/dx)^2)^3/2可以观察到,曲率与弧线的长度之间并没有直接的数学关系。
曲率的计算只与称为“二阶导数”的概念相关,而弧线的长度则需要通过积分来求解。
三、弧线长度和曲率的物理学应用弧线长度和曲率的关系在物理学中有广泛的应用。
以下是其中的几个例子:1. 光学系统中的透镜设计在光学系统中,透镜的曲率决定了光线的聚焦效果,而弧长则影响光线的传输距离。
通过研究弧线的长度和曲率之间的关系,可以设计出更加精确的透镜,提高光学系统的成像效果。
2. 电子学中的电路板设计在电子学中,电路板的设计通常需要考虑电子元件之间的布局和连接。
弧线的长度和曲率可以影响电路板的布线长度和连接的可靠性。
通过优化弧线的长度和曲率,可以减少电路板的空间占用,提高电子设备的性能和可靠性。
3. 车辆运动的轨迹规划在机器人或自动驾驶系统中,车辆需要根据预定的路径进行运动。
弧线的长度和曲率可以影响车辆的转弯半径和行驶距离。
通过研究弧线的长度和曲率之间的关系,可以优化车辆的轨迹规划,提高运动效率和安全性。
4. 引力场中的物体运动在物理学中,弧线的长度和曲率对于描述物体在引力场中的运动轨迹非常重要。

曲线的弧长与曲率的计算与性质曲线是我们经常在数学、物理等领域中遇到的概念。
当我们研究曲线的性质时,曲线的弧长和曲率是两个重要的参数。
本文将介绍曲线的弧长和曲率的计算方法,并探讨它们的性质。
一、曲线的弧长计算方法在几何学中,曲线的弧长是指曲线上两点之间的距离。
对于一条平面曲线来说,我们可以通过积分来计算其弧长。
具体计算方法如下:假设有一条曲线C,其方程为y = f(x),其中a ≤ x ≤ b。
我们可以将曲线分割成无穷多个小线段,然后对每个小线段求长度,并将这些长度累加起来,即可得到曲线C的弧长L。
设曲线上某一点P(x, y),其切线与x轴的夹角为θ,则小线段的长度可以通过勾股定理计算得到:ds = √(dx² + dy²) = √(1 + (dy/dx)²)dx将dx用x表示,即可得到弧长的积分表达式:L = ∫√(1 + (dy/dx)²)dx (a ≤ x ≤ b)通过求解上述积分,我们可以计算曲线的弧长。
二、曲线的曲率计算方法曲率是描述曲线弯曲程度的一个参数,它与曲线上某一点处的切线有关。
曲线的曲率可以通过以下公式计算:K = |dθ/ds| = |(d²y/dx²)/(1 + (dy/dx)²)^(3/2)|其中,dθ表示角度的变化量,ds表示弧长的微元。
我们可以根据上述公式,对曲线进行求导,然后带入相应的数值,即可得到曲线上某点的曲率K。
三、曲线弧长与曲率的性质1. 弧长与曲线的形状有关:对于相同起点和终点的两条曲线,其弧长不同,取决于曲线的形状。
比如,一条圆形的曲线与一条直线的曲线相比,弧长要更长。
2. 曲率描述曲线的弯曲程度:曲率大的地方,曲线的弯曲程度越大;曲率小的地方,曲线的弯曲程度越小。
通过计算曲率,我们可以描述曲线的局部形态。
3. 曲率与切线垂直:曲线上任意一点处的切线与曲线的法线(垂直于切线的直线)平行。




曲线的弧长与曲率在微积分学中,曲线的弧长和曲率是研究曲线性质的重要概念。
曲线的弧长是曲线上两点之间的距离,在物理、几何和工程等领域都有广泛的应用。
而曲率则描述了曲线弯曲的程度,是曲线几何形状的重要属性。
本文将从弧长和曲率的定义、计算方法以及它们之间的关系等方面进行探讨。
1. 弧长的定义和计算方法在平面直角坐标系中,设曲线C的参数方程为x=f(t),y=g(t),其中a≤t≤b。
我们希望计算曲线C上从点P到点Q的弧长。
假设P的参数值为t1,Q的参数值为t2。
首先,我们将弧长近似分为许多小线段,然后对这些小线段进行求和,即可得到总的弧长。
若将两个相邻点之间的距离表示为Δs,将其与曲线上相应的曲线段长度Δl进行比较,可以得到如下近似关系:Δs ≈ Δl。
通过不断缩小曲线上相邻点的数量和距离,我们可以得到越来越精确的弧长。
当曲线弧长的计算求和极限存在时,我们说曲线是可求长的。
对于参数方程x=f(t),y=g(t),我们可以先求出曲线上相邻两点P(t)和Q(t+Δt)的坐标,然后利用勾股定理求出Δl≈√(Δx)²+(Δy)²的近似值,再将这些近似值相加就可以得到曲线C的弧长L。
当Δt无限接近于0时,上述近似值趋于精确的弧长。
2. 曲率的定义和计算方法曲线的曲率描述了曲线弯曲的程度。
在平面直角坐标系中,曲线C的曲率表示为k。
对曲线上任意一点P(x,y),选择与该点相切的一条线段,该线段称为切线。
切线与曲线在P点处的夹角被称为曲线在该点的切角α。
切线的斜率由直线的斜率表示,可以通过求导得到。
曲线的曲率k定义为切线斜率对弧长s的导数,即k=dy/dx。
求解曲率的计算方法有多种,其中一种常用的方法是使用参数方程。
设曲线C的参数方程为x=f(t),y=g(t),对其分别关于参数t求导,即可得到曲线的导函数dx/dt和dy/dt。
然后,利用链式法则可以求得dy/dx=(dy/dt)/(dx/dt)。

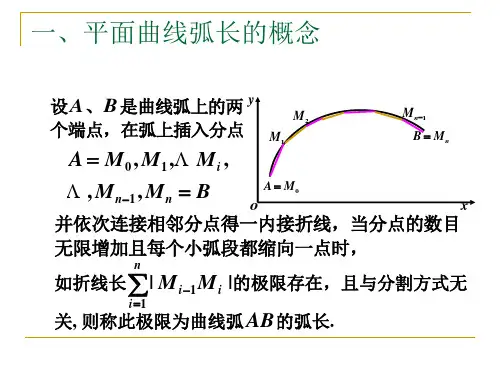
第十章 定积分的应用 3 平面曲线的弧长与曲率一、平面曲线的弧长设平面曲线C=⌒AB. 如图所示,在C 上从A 到B 依次取分点: A=P 0,P 1,P 2,…,P n-1,P n =B ,它们成为曲线C 的一个分割,记为T. 用线段联结T 中每相邻两点,得到C 的n 条弦P i-1P i (i=1,2,…,n),这n 条弦又成为C 的一条内接折线,记:T =ni 1max ≤≤|P i-1P i |,s T =∑=n1i i 1-i |P P |,分别表示最长弦的长度和折线的总长度。
定义1:对于曲线C 的无论怎样的分割T , 如果存在有限极限:0T lim →s T =s ,则称曲线C 是可求长的, 并把极限s 定义为曲线C 的弧长.定义2:设平面曲线C 由参数方程x=x(t), y=y(t), t ∈[α,β]给出. 如果x(t)与y(t)在[α,β]上连续可微,且x ’(t)与y ’(t)不同时为零 (即x ’2(t)+y ’2(t)≠0, t ∈[α,β]),则称C 为一条光滑曲线.定理:设曲线C 由参数方程x=x(t), y=y(t), t ∈[α,β]给出. 若C 为一光滑曲线,则C 是可求长的,且弧长为:s=⎰'+'βα22(t)y (t)x dt.证:对C 作任意分割T={P 0,P 1,…,P n },并设P 0与P n 分别对应t=α与t=β, 且P i (x i ,y i )=(x(t i ),y(t i )), i=1,2,…,n-1.于是,与T 对应得到区间[α,β]的一个分割T ’: α=t 0< t 1<t 2<…t n-1<t n =β.在T ’所属的每个小区间△i =[t i-1,t i ]上,由微分中值定理得△x i =x(t i )-x(t i-1)=x ’(ξi )△t i , ξi ∈△i ;△y i =y(t i )-y(t i-1)=y ’(ηi )△t i , ηi ∈△i . 从而C 的内接折线总长为s T =∑=∆+∆n1i 2i 2i y x =∑='+'n1i i 2i 2)(ηy )(ξx △t i .记σi =)(ηy )(ξx i 2i 2'+'-)(ξy )(ξx i 2i 2'+',则s T =[]∑=+'+'n1i i i 2i 2σ)(ηy )(ξx △t i .又由三角形不等式可得:|σi |≤||y ’(ηi )|-|y ’(ξi )||≤|y ’(ηi )-y ’(ξi )|. 由y ’(t)在[α,β]上连续,从而一致连续,∴对任给的ε>0, 存在δ>0, 当T '<δ时,只要ηi , ξi ∈△i ,就有|σi |≤|y ’(ηi )-y ’(ξi )|<α-βε, i=1,2,…,n. ∴|s T -∑='+'n1i i 2i 2)(ξy )(ξx △t i |=|∑=n1i i σ△t i |≤∑=n1i i |σ|△t i <ε,∴0T lim →s T =∑=→''+'n1i i 2i 20T )(ξy )(ξx lim △t i ,即s=⎰'+'βα22(t)y (t)x dt.注:1、若曲线C 由直线坐标方程y=f(x), x ∈[a,b]表示,则看作参数方程:x=x, y=f(x), x ∈[a,b]. 因此,当f(x)在[a,b]上连续可微时,此曲线即为一光滑曲线,其弧长公式为:s=⎰'+ba 2(x )f 1dx. 2、若曲线C 由极坐标方程r=r(θ), θ∈[α,β]表示,则 化为参数方程:x=r(θ)cos θ, y=r(θ)sin θ, θ∈[α,β]. 由x ’(θ)=r ’(θ)cos θ-r(θ)sin θ, y ’(θ)=r ’(θ)sin θ+r(θ)cos θ, 得:x ’2(θ)+y ’2(θ)=r 2(θ)+r ’2(θ),∴当r ’(θ)在[α,β]连续,且r(θ)与r ’(θ)不同时为零时,此极坐标曲线为一光滑曲线, 其弧长公式为:s=⎰'+βα22 )(θr )(θr d θ.例1:求摆线x=a(t-sint), y=a(1-cost)(a>0)一拱的孤长.解:∵x’(t)=a-acost; y’(t)=asint. ∴x’2(t)+y’2(t)=2a2(1-cost)=4a2sin22t.其弧长为s=⎰2π222tsin4a dt=4a⎰2π02tsin d⎪⎭⎫⎝⎛2t=8a.例2:求悬链线y=2ee-xx+从x=0到x=a>0那一段的弧长.解:∵y’=2ee-xx-. ∴1+y’2=2x-x2ee⎪⎪⎭⎫⎝⎛+.其弧长为s=⎰+a-xx2ee dx=2ee-aa-.例3:求心形线r=a(1+cosθ) (a>0)的周长.解:∵r’(θ)=-asinθ. ∴r2(θ)+r’2(θ)=4a2cos22θ.其周长为s=⎰2π02θacos2dθ=4a⎰2π02θcos d⎪⎭⎫⎝⎛2θ=8a.注:∵s(t)=⎰'+'tα22(t)y(t)x dt连续,∴dtds=22dtdydtdx⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛,即有ds=22dydx+. 特别称s(t)的微分dx为弧微分. (如左下图)PR为曲线在点P处的切线,在Rt△PQR中,PQ为dx,QR为dy,PR则为dx,这个三角形称为微分三角形。

曲线的弧长与曲率曲线是数学中常见的概念,而研究曲线的性质也是数学分析的重要内容之一。
在曲线的研究中,弧长和曲率被广泛应用于描述和分析曲线的特征。
本文将重点介绍曲线的弧长与曲率的概念、计算方法以及它们之间的关系。
一、曲线的弧长曲线的弧长是指曲线上两点之间的长度。
在平面几何中,我们经常使用直线段的长度来描述距离,但是对于曲线,由于其不是直线,所以无法直接使用直线段的长度来描述曲线间的距离。
曲线的弧长是通过将曲线分成无限多个微小的线段,然后对每个微小线段的长度进行累加得到。
计算曲线的弧长可以使用微积分中的积分方法。
设曲线函数为y=f(x),对于曲线上的一段很小的微小线段[Pn, Pn+1],则该微小线段的长度可以表示为:ΔL = √(Δx^2 + Δy^2)其中Δx和Δy分别为微小线段[Pn, Pn+1]在x轴和y轴上的长度变化。
通过将上述微小线段长度进行累加求和,可以得到曲线在给定区间[a, b]上的弧长L,表示为积分形式:L = ∫[a,b]√(1+(dy/dx)^2)dx其中dy/dx表示曲线的导数。
二、曲线的曲率曲线的曲率是描述曲线的弯曲程度的量。
对于曲线上的任意一点P,曲率是一个与该点有关的值,可以表示为曲线在该点处的切线与曲线的夹角的度量。
曲率的大小与曲线的曲率半径有关,曲率半径是曲线在该点处的切线与曲线夹角的倒数。
曲线的曲率可以通过曲线的参数方程来计算,参数方程表示曲线上的点与参数之间的关系。
设曲线的参数方程为[x(t), y(t)],则曲线的曲率可以表示为:K = |(dx/dt)(d^2y/dt^2) - (d^2x/dt^2)(dy/dt)| / [(dx/dt)^2 +(dy/dt)^2]^(3/2)其中dx/dt和dy/dt分别表示曲线参数关于t的导数,d^2x/dt^2和d^2y/dt^2分别表示曲线参数关于t的二阶导数。
三、弧长与曲率的关系曲线的弧长和曲率之间存在一定的关系。

空间曲线的弧长与曲率空间曲线弧长的计算是一个重要的数学问题,与曲率密切相关。
曲线的弧长和曲率在工程、物理学、计算机图形学等领域具有广泛的应用。
本文将探讨空间曲线的弧长计算方法和曲率的概念。
一、弧长的计算方法空间曲线的弧长是曲线上各点之间的距离积分。
设曲线的参数方程为 r(t) = (x(t), y(t), z(t)),曲线上两个点的坐标分别为 P(t₁) 和 P(t₂),则P(t) 到 P(s) 的弧长可以表示为:L = ∫[t₁, t₂] √[x'(t)² + y'(t)² + z'(t)²] dt其中,x'(t)、y'(t)和z'(t)分别表示曲线在 t 时刻的切线方向的导数。
二、曲率的概念曲率是描述曲线弯曲程度的量度。
对于平面曲线,曲率可以通过曲线切线的变化率来计算,但对于空间曲线,则需要引入副法线来描述曲率的变化情况。
空间曲线的曲率可通过以下公式计算:K = |dT/ds|其中,T 是曲线的切向量,ds 是弧长的微元。
三、空间曲线的弧长与曲率的关系弧长与曲率之间存在着紧密的关系。
一般来说,曲线的弧长越长,曲率变化越大。
具体而言,对于光滑曲线而言,如果曲线的曲率值始终为常数,那么弧长为直线长度。
而如果曲线的曲率变化较大,那么曲线的弧长将较长。
四、实际应用空间曲线的弧长和曲率在物理学、计算机图形学等领域具有广泛应用。
在物理学中,通过计算空间曲线的弧长和曲率,可以研究天体轨道的特性。
例如,科学家可以通过计算行星和卫星轨道的弧长和曲率来推断天体的质量和作用力。
在计算机图形学中,通过计算空间曲线的弧长和曲率,可以实现真实感图形的绘制。
例如,在绘制三维曲面时,可以使用弧长计算方法和曲率信息来确定光线的路径,从而产生逼真的阴影效果。
五、总结本文介绍了空间曲线的弧长与曲率的概念及其计算方法。
空间曲线的弧长是曲线上各点之间的距离积分,而曲率则是描述曲线弯曲程度的量度。
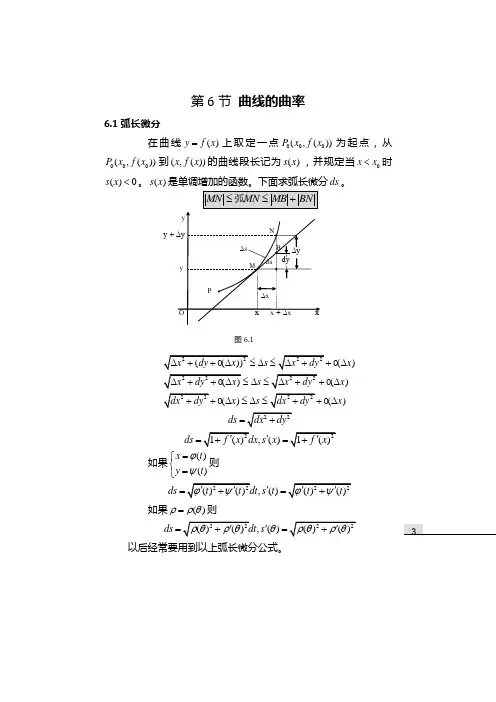
第6节 曲线的曲率6.1弧长微分在曲线()y f x =上取定一点000(,())P x f x 为起点,从000(,())P x f x 到(,())x f x 的曲线段长记为()s x ,并规定当0x x <时()0s x <。
()s x 是单调增加的函数。
下面求弧长微分ds 。
()()()()s x s x x s x ≤∆≤∆≤∆≤∆∆≤∆≤∆ds =,()ds s x '== 如果()()xt y t ϕψ=⎧⎨=⎩则,()ds s t '==如果()ρρθ=则,()ds s θ'==以后经常要用到以上弧长微分公式。
图6.1y +离 散数 学6.2曲线的曲率这节讨论曲线的曲率,也就是曲线的弯曲程度。
设曲线()y f x =在()00,()x f x 的切线0L 与x 轴正向的夹角为0θ,在()00,()x x f x x +∆+∆的切线x L ∆与x 轴正向的夹角为x θ∆。
经过x ∆,切线的夹角变化了0x θθθ∆∆=-设()00,()x f x 和()00,()x x f x x +∆+∆之间曲线的长为s ∆。
容易想见,()00,()x f x 和()00,()x x f x x +∆+∆之间曲线的曲率(弯曲程度)与θ∆成正比,与s ∆成反比,平均曲率()k x sθ∆∆=∆ 让0x ∆→求极限,就得到曲线()y f x =在()00,()x f x 的曲率(弯曲程度)000()lim ()limx x d k x k x s dsθθ∆→∆→∆=∆==∆ 下面我们求出d dsθ从而得到求曲率的计算公式。
用x 作参数 ()()s s x x θθ=⎧⎨=⎩()()2222tan ()1()cos 1tan ()1()()()1()f x d f x dx d f x dx f x d f x dxd f x dx f x θθθθθθθ'=''=''+='''+=''='+第1章集 合322()1()d f x d ds dxdxds f x θθ''=='⎡⎤+⎣⎦003220()()1()f x k x f x ''='⎡⎤+⎣⎦例子:求半径为r 的圆上一点的曲率。
导数的应用曲线的弧长与曲率计算导数的应用——曲线的弧长与曲率计算曲线是几何学中的重要概念,我们在日常生活中经常会遇到各种各样的曲线形状。
在数学中,对于曲线的研究和计算也有很多有趣的应用。
其中,导数的应用可以帮助我们计算曲线的弧长和曲率,进一步深化我们对曲线性质的理解。
本文将介绍导数在曲线的弧长和曲率计算中的具体应用。
一、曲线的弧长计算在数学中,曲线的弧长是指曲线上两点之间的实际距离。
我们可以通过导数来计算曲线的弧长。
假设有一条平面曲线y=f(x),我们希望计算曲线上从点A(x=a,y=f(a))到点B(x=b, y=f(b))的弧长。
首先,将曲线分割成无穷小的线段,假设一个无穷小线段的长度为ds。
根据勾股定理,该线段的长度可以表示为:ds = √(dx² + dy²)由导数的定义可知,dy/dx为曲线在某一点的斜率。
由此得到dy=dy/dx*dx。
将dy代入上式中,得到:ds = √(1+(dy/dx)²)*dx对上述表达式进行积分运算,就可以得到整个曲线上从A点到B点的弧长L的计算公式:L = ∫[a,b]√(1+(dy/dx)²)dx通过上述公式,我们可以使用导数来计算曲线上任意两点之间的弧长。
二、曲线的曲率计算曲率是指曲线在某一点上的弯曲程度,可以反映曲线的灵活性和形状。
我们可以通过导数来计算曲线的曲率。
假设有一条平面曲线y=f(x),我们希望计算曲线在点P(x, y)处的曲率。
曲率的计算公式为:κ = |dy/dx|/√(1+(dy/dx)²)³其中,|dy/dx|表示曲线在该点的斜率的绝对值。
曲率计算的实际应用场景非常广泛。
例如,在道路设计中需要考虑道路的弯曲程度,通过曲线的曲率计算可以帮助工程师设计出更符合交通规范和行车安全的道路。
通过导数的应用,我们可以结合曲线的弧长和曲率计算,更深入地研究和理解曲线的各种性质。
总结:在数学中,导数的应用可以帮助我们计算曲线的弧长和曲率,进一步深化对曲线性质的理解。
第十章 定积分的应用 3 平面曲线的弧长与曲率一、平面曲线的弧长设平面曲线C=⌒AB. 如图所示,在C 上从A 到B 依次取分点: A=P 0,P 1,P 2,…,P n-1,P n =B ,它们成为曲线C 的一个分割,记为T. 用线段联结T 中每相邻两点,得到C 的n 条弦P i-1P i (i=1,2,…,n),这n 条弦又成为C 的一条内接折线,记:T =ni 1max ≤≤|P i-1P i |,s T =∑=n1i i 1-i |P P |,分别表示最长弦的长度和折线的总长度。
定义1:对于曲线C 的无论怎样的分割T , 如果存在有限极限:0T lim →s T =s ,则称曲线C 是可求长的, 并把极限s 定义为曲线C 的弧长.定义2:设平面曲线C 由参数方程x=x(t), y=y(t), t ∈[α,β]给出. 如果x(t)与y(t)在[α,β]上连续可微,且x ’(t)与y ’(t)不同时为零 (即x ’2(t)+y ’2(t)≠0, t ∈[α,β]),则称C 为一条光滑曲线.定理10.1:设曲线C 由参数方程x=x(t), y=y(t), t ∈[α,β]给出. 若C 为一光滑曲线,则C 是可求长的,且弧长为:s=⎰'+'βα22(t)y (t)x dt. 证:对C 作任意分割T={P 0,P 1,…,P n },并设P 0与P n 分别对应t=α与t=β, 且P i (x i ,y i )=(x(t i ),y(t i )), i=1,2,…,n-1.于是,与T 对应得到区间[α,β]的一个分割T ’: α=t 0< t 1<t 2<…t n-1<t n =β.在T ’所属的每个小区间△i =[t i-1,t i ]上,由微分中值定理得△x i =x(t i )-x(t i-1)=x ’(ξi )△t i , ξi ∈△i ;△y i =y(t i )-y(t i-1)=y ’(ηi )△t i , ηi ∈△i . 从而C 的内接折线总长为s T =∑=∆+∆n1i 2i 2i y x =∑='+'n1i i 2i 2)(ηy )(ξx △t i .记σi =)(ηy )(ξx i 2i 2'+'-)(ξy )(ξx i 2i 2'+',则s T =[]∑=+'+'n1i i i 2i 2σ)(ηy )(ξx △t i .又由三角形不等式可得:|σi |≤||y ’(ηi )|-|y ’(ξi )||≤|y ’(ηi )-y ’(ξi )|. 由y ’(t)在[α,β]上连续,从而一致连续,∴对任给的ε>0, 存在δ>0, 当T '<δ时,只要ηi , ξi ∈△i ,就有|σi |≤|y ’(ηi )-y ’(ξi )|<α-βε, i=1,2,…,n. ∴|s T -∑='+'n1i i 2i 2)(ξy )(ξx △t i |=|∑=n1i i σ△t i |≤∑=n1i i |σ|△t i <ε,∴0T lim →s T =∑=→''+'n1i i 2i 20T)(ξy )(ξx lim △t i ,即s=⎰'+'βα22(t)y (t)x dt.注:1、若曲线C 由直线坐标方程y=f(x), x ∈[a,b]表示,则看作参数方程:x=x, y=f(x), x ∈[a,b]. 因此,当f(x)在[a,b]上连续可微时,此曲线即为一光滑曲线,其弧长公式为:s=⎰'+ba 2(x )f 1dx. 2、若曲线C 由极坐标方程r=r(θ), θ∈[α,β]表示,则 化为参数方程:x=r(θ)cos θ, y=r(θ)sin θ, θ∈[α,β]. 由x ’(θ)=r ’(θ)cos θ-r(θ)sin θ, y ’(θ)=r ’(θ)sin θ+r(θ)cos θ, 得:x ’2(θ)+y ’2(θ)=r 2(θ)+r ’2(θ),∴当r ’(θ)在[α,β]连续,且r(θ)与r ’(θ)不同时为零时,此极坐标曲线为一光滑曲线, 其弧长公式为:s=⎰'+βα22 )(θr )(θr d θ.例1:求摆线x=a(t-sint), y=a(1-cost)(a>0)一拱的孤长.解:∵x ’(t)=a-acost; y ’(t)=asint. ∴x ’2(t)+y ’2(t)=2a 2(1-cost)=4a 2sin 22t. 其弧长为s=⎰2π0222t sin 4a dt=4a ⎰2π02tsin d ⎪⎭⎫ ⎝⎛2t =8a.例2:求悬链线y=2e e -xx +从x=0到x=a>0那一段的弧长.解:∵y ’=2e e -x x -. ∴1+y ’2=2x-x 2ee ⎪⎪⎭⎫⎝⎛+. 其弧长为s=⎰+a 0-x x 2e e dx=2e e -aa -.例3:求心形线r=a(1+cos θ) (a>0)的周长. 解:∵r ’(θ)=-asin θ. ∴r 2(θ)+r ’2(θ)=4a 2cos 22θ.其周长为s=⎰2π02θacos 2d θ=4a ⎰2π02θcos d ⎪⎭⎫⎝⎛2θ=8a.注:∵s(t)=⎰'+'tα22(t)y (t)x dt 连续,∴dt ds =22dt dy dt dx ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛,即有ds=22dy dx +. 特别称s(t)的微分dx 为弧微分. (如左下图)PR 为曲线在点P 处的切线,在Rt △PQR 中,PQ 为dx ,QR 为dy ,PR 则为dx ,这个三角形称为微分三角形。
§3 平面曲线的弧长与曲率一 平面曲线的弧长先建立平面曲线弧长的概念,设C=AB 是一条没有自交点的非闭的平面曲线,在C 上从A 到B 依次取分点A=P 0,P 1,P 2,…,P n =B,它们成为对曲线C 的一个分割,记为T ,然后用线段连接T 中每相邻两点,得到C 的n 条弦1(1,2,...,)i i P P i n -=,这n 条弦又成为C 的一条内接折线,记||T||=max|P i-1P i |,11||nT i ii s PP -==∑分别表示最长弦的长度和折线的总长度。
定义1 如果存在有限极限||||0lim s T T s →=,即任给ε>0,恒存在δ>0,使得对于C 的任何分割T ,只要||T||<δ,就有|s T -s|<ε,曲线C 是可求长的,并把s 定义为曲线C 的弧长。
定理10.1 设曲线C 是一条没有自交点的非闭的平面曲线,由参数方程x=x(t),y=y(t),t ∈[α,β]给出,若x(t)、y(t)在[α,β]上连续可微,则C 是可求长的,且弧长为s βα=⎰。
证明 对C 作任一分割T={ P 0,P 1,P 2,…,P n },并设P0与Pn 分别对应t=α和t=β,且P i (x i ,y i )=(x(t i ),y(t i )),i=1,2,…,n -1,于是与T 对应得到区间[α,β]的一个分割T':α=t 0,t 1,t 2,…,t n =β。
现在用反证法先证明||||0lim ||||0T T →'=.假设||||0lim ||||0T T →'≠,则存在ε0>0,对于任何δ>0,都可以找到一个分割T 使得||T||<δ而同时||T'||>ε0,从而可以找到C 上两点Q'和Q'',使得|Q''Q'|<δ,而它们对应的参量t'和t''满足|t't''|≥ε0,依次取δ=1/n,n=1,2,…,则得到两个点列{Q'n }和{Q''n }和它们对应的参量数列{t'n }和{t''n },它们满足|Q n ''Q n '|<1/n, |t'n t''n |≥ε0,由致密性定理,存在子列{}{}k kn n t t '''及,和t*和t**∈[α,β],使得lim *,lim **k knn k k t t t t →∞→∞'''==,显然|t*-t**|≥ε0,即t*≠t**。
§ 3 平面曲线的弧长与曲率
一、平面曲线的弧长 1、平面曲线的弧长的概念
一条线段的长度可直接度量,但一条曲线段的“长度”一般却不能直接度量,因此需用不同的方法来
求. 定义曲线弧长的基本思想是局部以直代曲 , 即用内接折线总长的极限定义弧长 .
定义1 可求长曲线
设平面曲线C 由参数方程()
()
x x t y y t =⎧⎨
=⎩ (t αβ≤≤)给出,设01{,,
,}n P t t t =是[,αβ]的一个划分
[0,n t t αβ==],即01n t t t αβ=<<<=,它们在曲线C 上所对应的点为000((),())M x t y t =,
111((),())M x t y t =,…,((),())n n n M x t y t =。
从端点0M 开始用线段一次连接这些分点0M ,1M ,…,n M 得到曲线的一条内接折线,用1i i M M -来表示1i i M M -的长度,则内接折线总长度为
11
1
n n
n i i i i S M M -====∑
曲线C 的弧长S 定义为内接折线的总长在max 0i p t =→时的极限:
10
1
1
lim lim n n
i i p p i i S M M -→→====∑
如果S 存在且为有限,则称C 为可求长曲线。
定义2 设曲线C :()
()
x x t y y t =⎧⎨
=⎩ (t αβ≤≤),且()x t ,()y t 在[,αβ]上连续可微,且导数()x t ',()y t '在[,αβ]上不同时为0(曲线C 在[,αβ]无自交点),则曲线C 称为光滑曲线.
2、弧长公式
定理10.1设曲线C 为如上的光滑曲线,则曲线C 是可求长的,且弧长S 为:
S β
β
α
α
==⎰
⎰
注:利用微元法推导公式
注:其它形式的弧长公式
(1)设()y y x =在[a,b]上可微且导数()y x '可积,则曲线()y y x =(a ≤x ≤b )的弧长S 为:
a
S =⎰
(2)若曲线极坐标方程()r r θ=,αθβ≤≤,则当()r θ在[,αβ]上可微,且()r θ'可积时,
S β
α
θ=⎰
(3)空间曲线()()()x x t y y t z z t =⎧⎪
=⎨⎪=⎩
(t αβ≤≤),弧长S 为
S βα
=⎰
其中x(t),y(t),z(t)在[,αβ]上可微,导数()x t ',()y t ',()z t '在[,αβ]上可积且曲线C 在 [,αβ]上无自交点。
补例1 求圆周cos x R t =,sin y R t =,02t π≤≤的弧长S 。
补例2 求抛物线2
12
y x =,01x ≤≤的弧长S 。
例3、求椭圆22221x y a b +=(b>a>0)的弧长S 。
3、弧长的微分
设C :()()x x t y y t =⎧⎨=⎩
(t αβ≤≤)是光滑曲线(()x t ',()y t '在[,αβ]连续且2()x t '+2
()0y t '≠);
且无自交点。
若把公式中的积分上限β改为t ,就得到曲线C ,由端点0M 到动点((),())M x t y t 的一段弧长。
t
S α
=⎰
由上限函数的可微性知()S t '
存在,()dS t dS dt ==二、平面曲线的曲率 1、曲率的概念
曲线的弯曲程度不仅与其切线方形的变化角度ϕ∆的大小有关,而且还与所考察的曲线的弧长S ∆有关,并且曲率与
ϕ成正比,与S 成反比。
即一般曲线的弯曲程度可用k S
ϕ
∆=
∆,其中k :曲线段AB 的平均变化率;ϕ∆:曲线段AB 上切线方向的角度;S ∆:曲线段AB 的弧长。
例1、半径为R 的圆:1
k S S R R
ϕααα∆∆∆=
===∆∆∆⋅。
对于一般的曲线,如何刻画它在一点处的弯曲程度呢?
0lim
s k S ϕ
→∆=∆,称为曲线在A 点的曲率,即0lim s d k dS S
ϕϕ→∆==∆
2、曲率的计算
记()y y x =二阶可微,则在点x 处的曲率为: 因为tg y ϕ'=,arctgy ϕ'=,所以
2211d y y d dx dx y y ϕϕ''''
=⇒=''++
,又因为dS =所以 ()
3/221d y k dS y ϕ''
=
='+ 例1、求2
12
y x =
在任一点的曲率。
3、曲率圆和曲率半径
过点(x ,y(x))且与y =y (x )在该点有相同的一阶及二阶导数的圆2
2
2
()()x a y b R -+-=称为曲率圆。
曲率圆的中心和半径分别称为曲率中心和曲率半径。
如何求曲线上一点(x ,y(x))处的曲率圆呢?
因为1R k =
,()
3/221y k y ''
='+,则(a,b )在过(x ,y(x))的法线上:1()()()Y y x X x y x -=--'。
例1、 求2
12
y x =
在点(0,0)的曲率圆方程? 作业 P252:1(1)、(3)、(5)
§ 4 旋转曲面的面积
一、微元法
提前在§ 1讲授
二 、旋转曲面的面积
用微元法推出旋转曲面的面积公式:
设y =y(x)于[a,b]上非负,且连续可微,该曲线绕x 轴旋转后所得的旋转面的侧面积:
2b
a
S π=⎰
曲线方程为 ],[ , )(b a x x f y ∈=时,⎰
'+=⇒b
a
dx x f x f )(1)(2S 2π
;
曲线方程为 ],[ , )( , )(βαχ∈==t t y y t x 时,⎰
'+'=⇒β
α
χπdt t y t x y )()()
(2S 22 .
例1 求半径为r 的球带的面积S.
例2
作业P255:1(2)、(4),3(1)。