自动控制原理 时域分析

实验二 线性系统时域响应分析一、实验目的1．熟练掌握step( )函数和impulse( )函数的使用方法，研究线性系统在单位阶跃、单位脉冲及单位斜坡函数作用下的响应。

2．通过响应曲线观测特征参量ζ和n ω对二阶系统性能的影响。

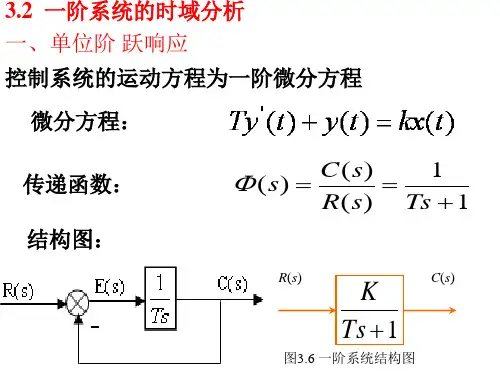
二、基础知识及MATLAB 函数（一）基础知识时域分析法直接在时间域中对系统进行分析，可以提供系统时间响应的全部信息，具有直观、准确的特点。

为了研究控制系统的时域特性，经常采用瞬态响应（如阶跃响应、脉冲响应和斜坡响应）。

本次实验从分析系统的性能指标出发，给出了在MATLAB 环境下获取系统时域响应和分析系统的动态性能和稳态性能的方法。

用MATLAB 求系统的瞬态响应时，将传递函数的分子、分母多项式的系数分别以s 的降幂排列写为两个数组num 、den 。

由于控制系统分子的阶次m 一般小于其分母的阶次n ，所以num 中的数组元素与分子多项式系数之间自右向左逐次对齐，不足部分用零补齐，缺项系数也用零补上。

1．用MATLAB 求控制系统的瞬态响应1）阶跃响应 求系统阶跃响应的指令有：step(num,den) 时间向量t 的范围由软件自动设定，阶跃响应曲线随即绘出step(num,den,t) 时间向量t 的范围可以由人工给定（例如t=0:0.1:10）[y ，x]=step(num,den) 返回变量y 为输出向量，x 为状态向量在MATLAB 程序中，先定义num,den 数组，并调用上述指令，即可生成单位阶跃输入信号下的阶跃响应曲线图。

考虑下列系统：25425)()(2++=s s s R s C 该系统可以表示为两个数组，每一个数组由相应的多项式系数组成，并且以s的降幂排列。

则MATLAB 的调用语句：num=[0 0 25]; %定义分子多项式 den=[1 4 25]; %定义分母多项式step(num,den) %调用阶跃响应函数求取单位阶跃响应曲线grid %画网格标度线 xlabel(‘t/s’),ylabel(‘c(t)’) %给坐标轴加上说明 title(‘Unit -step Respinse of G(s)=25/(s^2+4s+25)’) %给图形加上标题名 则该单位阶跃响应曲线如图2-1所示：为了在图形屏幕上书写文本，可以用text 命令在图上的任何位置加标注。

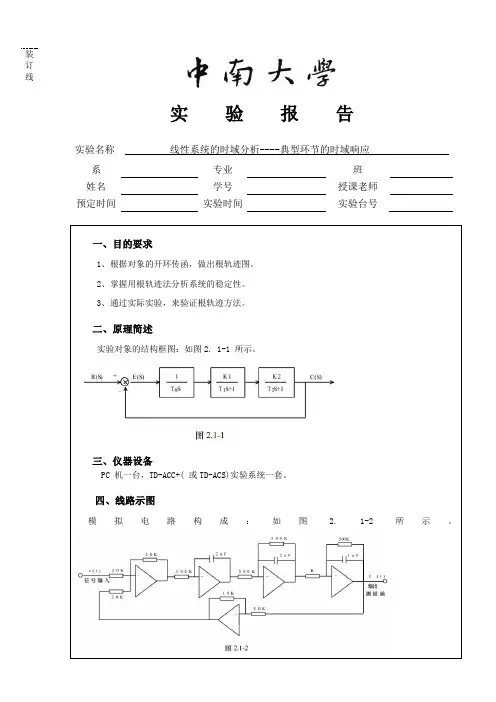
实验二 控制系统稳定性分析和时域响应分析一、实验目的与要求1、熟悉系统稳定性的Matlab 直接判定方法和图形化判定方法；2、掌握如何使用Matlab 进行控制系统的动态性能指标分析；3、掌握如何使用Matlab 进行控制系统的稳态性能指标分析。

二、实验类型设计三、实验原理及说明1. 稳定性分析 1）系统稳定的概念经典控制分析中，关于线性定常系统稳定性的概念是：若控制系统在初始条件和扰动共同作用下，其瞬态响应随时间的推移而逐渐衰减并趋于原点(原平衡工作点)，则称该系统是稳定的，反之，如果控制系统受到扰动作用后，其瞬态响应随时间的推移而发散，输出呈持续震荡过程，或者输出无限偏离平衡状态，则称该系统是不稳定的。

2）系统特征多项式以线性连续系统为例，设其闭环传递函数为nn n n mm m m a s a s a s a b s b s b s b s D s M s ++++++++==----11101110......)()()(φ 式中，n n n n a s a s a s a s D ++++=--1110...)(称为系统特征多项式；0...)(1110=++++=--n n n n a s a s a s a s D 为系统特征方程。

3）系统稳定的判定对于线性连续系统，其稳定的充分必要条件是：描述该系统的微分方程的特征方程具有负实部，即全部根在左半复平面内，或者说系统的闭环传递函数的极点均位于左半s 平面内。

对于线性离散系统，其稳定的充分必要条件是：如果闭环系统的特征方程根或者闭环传递函数的极点为n λλλ,...,21，则当所有特征根的模都小于1时，即),...2,1(1n i i =<λ，该线性离散系统是稳定的，如果模的值大于1时，则该线性离散系统是不稳定的。

4）常用判定语句2.动态性能指标分析系统的单位阶跃响应不仅完整反映了系统的动态特性，而且反映了系统在单位阶跃信号输入下的稳定状态。

自动控制原理实验报告《线性控制系统时域分析》一、实验目的1. 理解线性时间不变系统的基本概念，掌握线性时间不变系统的数学模型。

2. 学习时域分析的基本概念和方法，掌握时域分析的重点内容。

3. 掌握用MATLAB进行线性时间不变系统时域分析的方法。

二、实验内容本实验通过搭建线性时间不变系统，给出系统的数学模型，利用MATLAB进行系统的时域测试和分析，包括系统的时域性质、单位脉冲响应、单位阶跃响应等。

三、实验原理1. 线性时间不变系统的基本概念线性时间不变系统（Linear Time-Invariant System，简称LTI系统）是指在不同时间下的输入信号均可以通过系统输出信号进行表示的系统，它具有线性性和时不变性两个重要特性。

LTI系统的数学模型可以表示为：y(t) = x(t) * h(t)其中，y(t)表示系统的输出信号，x(t)表示系统的输入信号，h(t)表示系统的冲激响应。

2. 时域分析的基本概念和方法时域分析是一种在时间范围内对系统进行分析的方法，主要涉及到冲激响应、阶跃响应、单位脉冲响应等方面的内容。

针对不同的输入信号，可以得到不同的响应结果，从而确定系统的时域特性。

四、实验步骤与结果1. 搭建线性时间不变系统本实验中，实验者搭建了一个简单的一阶系统，系统的阻尼比为0.2，系统时间常数为1。

搭建完成后，利用信号发生器输出正弦信号作为系统的输入信号。

2. 获取系统的响应结果利用MATLAB进行系统的时域测试和分析，得到了系统的冲激响应、单位阶跃响应和单位脉冲响应等结果。

其中，冲激响应、阶跃响应和脉冲响应分别如下所示：冲激响应：h(t) = 0.2e^(-0.2t) u(t)阶跃响应：H(t) = 1-(1+0.2t) e^(-0.2t) u(t)脉冲响应：g(t) = h(t) - h(t-1)3. 绘制响应图表通过绘制响应图表，可以更好地展示系统的时域性质。

下图展示了系统的冲激响应、阶跃响应和脉冲响应的图表。

自动控制原理_线性系统时域响应分析1.线性系统时域响应概念线性系统是指其输入与输出之间存在线性关系的系统。

时域响应是指系统在时域上对不同输入信号的响应情况。

时域响应可以用系统的微分方程表示，也可以通过系统的冲激响应来表示。

2.常见的线性系统时域响应方法2.1零状态响应零状态响应是指系统在无初始条件下对输入信号的响应。

常用的分析方法有拉氏变换和复频域分析法。

拉氏变换法可以将微分方程转化为代数方程，从而得到系统的传递函数。

复频域分析法通过将时间域信号变换到复频域，进而进行频域分析。

2.2零输入响应零输入响应是指系统在只有初始条件而没有输入信号的情况下的响应。

常用分析方法有状态方程法和拉氏变换法。

状态方程法将系统表示为一组一阶微分方程的形式，通过求解状态方程可以得到系统的零输入响应。

拉氏变换法可以将初始条件转化为代数方程进行求解。

2.3总响应总响应是指系统在有输入信号和初始条件的情况下的响应。

常用分析方法有零输入响应法和零状态响应法。

零输入响应法通过去除输入信号的影响，只考虑系统的初始条件来求解系统的响应。

零状态响应法则相反，通过去除初始条件的影响，只考虑输入信号来求解系统的响应。

最后，将两者相加得到系统的总响应。

3.线性系统时域响应的应用线性系统时域响应的分析方法可以应用于各种实际工程问题中。

例如，可以通过时域响应分析来评估系统的稳定性、性能和抗干扰能力。

此外，时域响应分析也可以用于设计控制器和参数优化。

通过对系统的时域响应进行分析和改进，可以使得系统更加可靠、稳定和高效。

4.总结线性系统时域响应分析是自动控制原理中的重要内容，可以应用于各种实际工程问题中。

本文介绍了线性系统时域响应的概念、方法和应用。

时域响应的分析方法包括零状态响应、零输入响应和总响应分析，分别适用于不同的问题和要求。

了解和掌握线性系统时域响应分析方法对于设计和优化控制系统具有重要意义。