自动控制原理第三章线性系统的时域分析

第3章线性系统的时域分析与校正3.1 概述系统的数学模型建立后，便可对系统进行分析和校正。

分析和校正是自动控制原理课程的两大任务。

系统分析是由已知的系统模型确定系统的性能指标；校正是根据需要在系统中加入一些机构和装置并确定相应的参数，用以改善系统性能，使其满足所要求的性能指标。

系统分析的目的在于“认识”系统，系统校正的目的在于“改造”系统。

系统的分析校正方法一般有时域法、根轨迹法和频域法，本章介绍时域法。

3.1.1 时域法的作用和特点时域法是一种直接在时间域中对系统进行分析校正的方法，具有直观，准确的优点，它可以提供系统时间响应的全部信息，但在研究系统参数改变引起系统性能指标变化的趋势这一类问题，以及对系统进行校正设计时，时域法不是非常方便。

时域法是最基本的分析方法，该方法引出的概念、方法和结论是以后学习复域法、频域法等其他方法的基础。

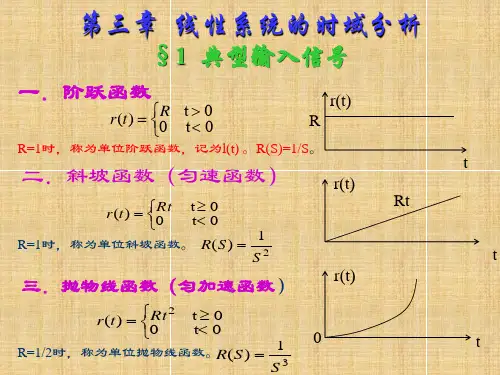
3．1．2 时域法常用的典型输入信号要确定系统性能的优劣，就要在同样的输入条件激励下比较系统的行为。

为了在符合实际情况的基础上便于实现和分析计算，时域分析法中一般采用如表3-1中的典型输入信号。

3．1．3 系统的时域性能指标如第一章所述，对控制系统的一般要求归纳为稳、准、快。

工程上为了定量评价系统性能好坏，必须给出控制系统的性能指标的准确定义和定量计算方法。

稳定是控制系统正常运行的基本条件。

系统稳定，其响应过程才能收敛，研究系统的性能（包括动态性能和稳态性能）才有意义。

实际物理系统都存在惯性，输出量的改变是与系统所储有的能量有关的。

系统所储有的能量的改变需要有一个过程。

在外作用激励下系统从一种稳定状态转换到另一种稳定状态需要一定的时间。

一个稳定系统的典型阶跃响应如图3-1所示。

响应过程分为动态过程（也称为过渡过程）和稳态过程，系统的动态性能指标和稳态性能指标就是分别针对这两个阶段定义的。

表3-1 时域分析法中的典型输入信号名称)(tr时域关系时域图形)(sR复域关系例单位脉冲函数⎩⎨⎧≠=∞=)(tttδ⎰=1)(dttδdtd1s⨯撞击作用后坐力电脉冲单位阶跃函数⎩⎨⎧<≥=1)(1ttts1开关输入单位斜坡函数⎩⎨⎧<≤=)(ttttf21s等速跟踪信号单位加速度函数⎪⎩⎪⎨⎧<≥=21)(2ttttf31s1 动态性能系统动态性能是以系统阶跃响应为基础来衡量的。

名校考研真题第3章　线性系统的时域分析一、选择题1．线性定常系统对某输入信号的响应已知，则求该系统对输入信号导数的响应，可通过把系统对该输入信号响应的（）来求取；而求系统对该输入信号的积分的响应，可通过系统对该信号响应的（）来求取。

[北京理工大学研]A．导数，导数B．积分，积分C．导数，积分D．积分，导数【答案】C2．某系统的开环传递函数，该系统是（）。

[南京理工大学研]A．Ⅰ型三阶系统B．Ⅲ型三阶系统C．Ⅲ型两阶系统D．Ⅰ型两阶系统【答案】A【解析】由于积分环节个数为1，所以选A 。

3．单位反馈控制系统的开环传递函数为，其开环增益和时间常数分别为（ ）。

[南京理工大学研]A ．20，5B ．50，0.2C ．10，5D ．10，0.2【答案】D 【解析】将传递函数改写成如下形式，开环增益和时间常数分别为10，0.2。

4．二阶振荡环节中，三个有定义的频率为：为无阻尼自然频率为有阻尼自然频率为谐振频率，它们之间的大小关系为( )。

[清华大学研]A．B ．C ．D ．【答案】B【解析】，显然。

5．闭环传递函数为的单位脉冲响应曲线，在处的值为( )。

[南京理工大学研]A．B．C．D．0【答案】B【解析】，所以当时，。

6．系统校正中引入“偶极子”的作用是改善系统的（）。

[东南大学研]A．稳态特性B．动态特性C．稳定性D．以上说法均不对【答案】A【解析】偶极子可以产生很大的开环增益而对系统的动态性能影响不大。

7．对高阶系统常常用主导极点的概念和偶极子对的方法进行简化，进而简化计算过程。

下面是几个简化式子，正确的是（）。

[南京理工大学]A．B．C．D．【答案】B【解析】利用闭环主导极点和偶极子对对系统进行化简时应该保证系统的开环增益不变。

二、填空题1．在反馈控制系统中，设置______或______可以消除或减小稳态误差。

[南京邮电大学研]【答案】开环增益；题型系统型次2．当系统的输入信号为单位斜坡函数时，______型以上的系统，才能使系统的稳态误差为零。

第3章线性系统的时域分析学习要点1控制系统时域响应的基本概念，典型输入信号及意义；2控制系统稳定性的概念、代数稳定判据及应用；3控制系统的时域指标，一阶二阶系统的阶跃响应特性与时域指标计算；4高阶系统时域分析中主导极点和主导极点法；5 控制系统稳态误差概念、计算方法与误差系数，减小稳态误差的方法。

思考与习题祥解题思考与总结下述问题。

（1）画出二阶系统特征根在复平面上分布的几种情况，归纳ξ值对二阶系统特征根的影响规律。

ω对二阶系统阶跃响应特性的影响规律。

（2）总结ξ和n（3）总结增加一个零点对二阶系统阶跃响应特性的影响规律。

（4）分析增加一个极点可能对二阶系统阶跃响应特性有何影响（5）系统误差与哪些因素有关试归纳减小或消除系统稳态误差的措施与方法。

（6）为减小或消除系统扰动误差，可采取在系统开环传递函数中增加积分环节的措施。

请问，该积分环节应在系统结构图中如何配置，抗扰效果是否与扰动点相关答：（1）二阶系统特征根在复平面上分布情况如图所示。

图 二阶系统特征根在复平面上的分布当0ξ=，二阶系统特征根是一对共轭纯虚根，如图中情况①。

当01ξ<<，二阶系统特征根是一对具有负实部的共轭复数根，变化轨迹是以n ω为半径的圆弧，如图中情况②。

当1ξ=，二阶系统特征根是一对相同的负实根，如图中情况③。

当1ξ>，二阶系统特征根是一对不等的负实根，如图中情况④。

（2）ξ和n ω是二阶系统的两个特征参量。

ξ是系统阻尼比，描述了系统的平稳性。

当0ξ=，二阶系统特征根是一对共轭纯虚根，二阶系统阶跃响应为等幅振荡特性，系统临界稳定。

当01ξ<<，二阶系统特征根是一对具有负实部的共轭复数根，二阶系统阶跃响应为衰减振荡特性，系统稳定。

ξ越小，二阶系统振荡性越强，平稳性越差；ξ越大，二阶系统振荡性越弱，平稳性越好。

因此，二阶系统的时域性能指标超调量由ξ值唯一确定，即001_100%2⨯=-πξξσe。

自动控制原理实验报告《线性控制系统时域分析》一、实验目的1. 理解线性时间不变系统的基本概念，掌握线性时间不变系统的数学模型。

2. 学习时域分析的基本概念和方法，掌握时域分析的重点内容。

3. 掌握用MATLAB进行线性时间不变系统时域分析的方法。

二、实验内容本实验通过搭建线性时间不变系统，给出系统的数学模型，利用MATLAB进行系统的时域测试和分析，包括系统的时域性质、单位脉冲响应、单位阶跃响应等。

三、实验原理1. 线性时间不变系统的基本概念线性时间不变系统（Linear Time-Invariant System，简称LTI系统）是指在不同时间下的输入信号均可以通过系统输出信号进行表示的系统，它具有线性性和时不变性两个重要特性。

LTI系统的数学模型可以表示为：y(t) = x(t) * h(t)其中，y(t)表示系统的输出信号，x(t)表示系统的输入信号，h(t)表示系统的冲激响应。

2. 时域分析的基本概念和方法时域分析是一种在时间范围内对系统进行分析的方法，主要涉及到冲激响应、阶跃响应、单位脉冲响应等方面的内容。

针对不同的输入信号，可以得到不同的响应结果，从而确定系统的时域特性。

四、实验步骤与结果1. 搭建线性时间不变系统本实验中，实验者搭建了一个简单的一阶系统，系统的阻尼比为0.2，系统时间常数为1。

搭建完成后，利用信号发生器输出正弦信号作为系统的输入信号。

2. 获取系统的响应结果利用MATLAB进行系统的时域测试和分析，得到了系统的冲激响应、单位阶跃响应和单位脉冲响应等结果。

其中，冲激响应、阶跃响应和脉冲响应分别如下所示：冲激响应：h(t) = 0.2e^(-0.2t) u(t)阶跃响应：H(t) = 1-(1+0.2t) e^(-0.2t) u(t)脉冲响应：g(t) = h(t) - h(t-1)3. 绘制响应图表通过绘制响应图表，可以更好地展示系统的时域性质。

下图展示了系统的冲激响应、阶跃响应和脉冲响应的图表。

自动控制原理_线性系统时域响应分析1.线性系统时域响应概念线性系统是指其输入与输出之间存在线性关系的系统。

时域响应是指系统在时域上对不同输入信号的响应情况。

时域响应可以用系统的微分方程表示，也可以通过系统的冲激响应来表示。

2.常见的线性系统时域响应方法2.1零状态响应零状态响应是指系统在无初始条件下对输入信号的响应。

常用的分析方法有拉氏变换和复频域分析法。

拉氏变换法可以将微分方程转化为代数方程，从而得到系统的传递函数。

复频域分析法通过将时间域信号变换到复频域，进而进行频域分析。

2.2零输入响应零输入响应是指系统在只有初始条件而没有输入信号的情况下的响应。

常用分析方法有状态方程法和拉氏变换法。

状态方程法将系统表示为一组一阶微分方程的形式，通过求解状态方程可以得到系统的零输入响应。

拉氏变换法可以将初始条件转化为代数方程进行求解。

2.3总响应总响应是指系统在有输入信号和初始条件的情况下的响应。

常用分析方法有零输入响应法和零状态响应法。

零输入响应法通过去除输入信号的影响，只考虑系统的初始条件来求解系统的响应。

零状态响应法则相反，通过去除初始条件的影响，只考虑输入信号来求解系统的响应。

最后，将两者相加得到系统的总响应。

3.线性系统时域响应的应用线性系统时域响应的分析方法可以应用于各种实际工程问题中。

例如，可以通过时域响应分析来评估系统的稳定性、性能和抗干扰能力。

此外，时域响应分析也可以用于设计控制器和参数优化。

通过对系统的时域响应进行分析和改进，可以使得系统更加可靠、稳定和高效。

4.总结线性系统时域响应分析是自动控制原理中的重要内容，可以应用于各种实际工程问题中。

本文介绍了线性系统时域响应的概念、方法和应用。

时域响应的分析方法包括零状态响应、零输入响应和总响应分析，分别适用于不同的问题和要求。

了解和掌握线性系统时域响应分析方法对于设计和优化控制系统具有重要意义。

第三章 线性系统的时域分析与校正习题及答案3-1 已知系统脉冲响应t e t k 25.10125.0)(-=试求系统闭环传递函数)(s Φ。

解 Φ()()./(.)s L k t s ==+00125125 3-2 设某高阶系统可用下列一阶微分方程T c t c t r t r t ••+=+()()()()τ近似描述，其中，1)(0<-<τT 。

试证系统的动态性能指标为 T T T t d ⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛-+=τln 693.0t T r =22. T T T t s ⎥⎦⎤⎢⎣⎡-+=)ln(3τ 解 设单位阶跃输入ss R 1)(= 当初始条件为0时有：11)()(++=Ts s s R s C τ 11111)(+--=⋅++=∴Ts T s s Ts s s C ττC t h t T Te t T()()/==---1τ 1) 当 t t d = 时h t T Te t td ()./==---051τ12=--T T e t T d τ/ ; Tt TT d-⎪⎭⎫ ⎝⎛-=-τln 2ln ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=∴T T T t d τln 2ln2) 求t r （即)(t c 从1.0到9.0所需时间)当 Tt eTT t h /219.0)(---==τ; t T T T 201=--[ln()ln .]τ 当 Tt eTT t h /111.0)(---==τ; t T T T 109=--[ln()ln .]τ 则 t t t T T r =-==21090122ln ... 3) 求 t sTt s s eTT t h /195.0)(---==τ ]ln 3[]20ln [ln ]05.0ln [ln TT T T T T T T T t s τττ-+=+-=--=∴3-3 一阶系统结构图如图3-45所示。

要求系统闭环增益2=ΦK ，调节时间4.0≤s t s ，试确定参数21,K K 的值。