凸函数判定方法的研究要点
- 格式:doc
- 大小:983.50 KB
- 文档页数:19


凸函数开题报告凸函数开题报告一、引言在数学领域中,凸函数是一种非常重要的概念。
它具有许多独特的性质和应用,被广泛应用于优化问题、经济学、物理学等各个领域。
本文将对凸函数的定义、性质以及一些应用进行探讨。
二、凸函数的定义凸函数是指定义在实数域上的函数,满足以下性质:对于任意两个实数x1和x2以及任意实数α(0≤α≤1),函数值f(αx1+(1-α)x2) ≤ αf(x1)+(1-α)f(x2)。
这个不等式被称为凸函数的凸性条件。
三、凸函数的性质1. 一阶凸性条件:对于定义在开区间(a,b)上的函数f(x),若对于任意的x1和x2(a<x1<x2<b)以及任意的α(0<α<1),有f(αx1+(1-α)x2) ≤ αf(x1)+(1-α)f(x2),则称函数f(x)在开区间(a,b)上是凸函数。
类似地,若不等式取反,则称函数f(x)是凹函数。
2. 二阶凸性条件:对于定义在开区间(a,b)上的函数f(x),若对于任意的x0∈(a,b),f''(x0)≥0,则称函数f(x)在开区间(a,b)上是凸函数。
类似地,若f''(x0)≤0,则称函数f(x)是凹函数。
3. 凸函数的判定方法:对于定义在开区间(a,b)上的函数f(x),若f'(x)在(a,b)上单调递增,则f(x)是凸函数。
同样地,若f'(x)在(a,b)上单调递减,则f(x)是凹函数。
四、凸函数的应用1. 优化问题:凸函数在优化问题中有着广泛的应用。
在约束条件下,凸函数的最小值或最大值往往可以通过求解一阶或二阶导数为零的方程得到。
例如,在经济学中,凸函数可以用来描述效用函数,从而求解最大化效用的问题。
2. 经济学:凸函数在经济学中有着重要的应用。
例如,生产函数、需求函数等经济学模型往往可以用凸函数来描述。
凸函数的性质可以帮助经济学家分析经济现象,并作出合理的决策。
3. 物理学:凸函数在物理学中也有一定的应用。

凸函数的性质研究毕业论文完整版凸函数是数学分析中一个重要的概念,具有广泛的应用。
在本篇毕业论文中,我将对凸函数的性质进行研究和探讨。
首先,我将介绍凸函数的定义和基本性质。
凸函数是指在定义域上的任意两点所连线的斜率都大于等于函数曲线上相应点的斜率。
简单来说,对于凸函数而言,函数曲线上的任意两点的切线均位于函数曲线上方。
这个定义可以很好地反映凸函数的凸起性质。
接下来,我将讨论凸函数的一阶导数和二阶导数的关系。
根据凸函数的定义,可以得出结论:对于函数的一阶导数,如果它是递增的,则该函数是凸函数;对于函数的二阶导数,如果它是非负的,则该函数是凸函数。
这一结论有助于我们通过导数的信息来判断函数的凸性质。
然后,我将探讨凸函数的性质在优化问题中的应用。
凸函数在优化问题中起到了重要的作用。
由于其凸起的性质,凸函数在求最优解的问题中往往能够确保找到全局最优解。
这一特性在实际问题中有着广泛的应用,比如投资组合优化、机器学习中的支持向量机等。
最后,我将研究凸函数的拓展性质。
除了一般的凸函数,还有一些特殊的凸函数形式,比如凸锥函数、凸二次规划等。
这些凸函数的研究将会进一步丰富我们对凸函数的认识,并提供更多的数学工具和方法。
通过对凸函数性质的研究,我们可以更好地理解凸函数的特性和应用。
凸函数不仅在数学领域有着广泛的研究价值,而且在实际问题中也有很多应用价值。
通过深入研究凸函数的性质,我们可以为解决优化问题和最优化问题提供更多的数学工具和方法。
总之,凸函数的性质研究是一个复杂且有意义的课题。
本篇毕业论文将通过介绍凸函数的定义和基本性质,探讨凸函数的一阶和二阶导数的关系,讨论凸函数在优化问题中的应用,以及研究凸函数的拓展性质等方面,对凸函数的性质进行深入的研究和探讨。
希望通过这篇毕业论文的研究,对凸函数的理解和应用有所帮助。
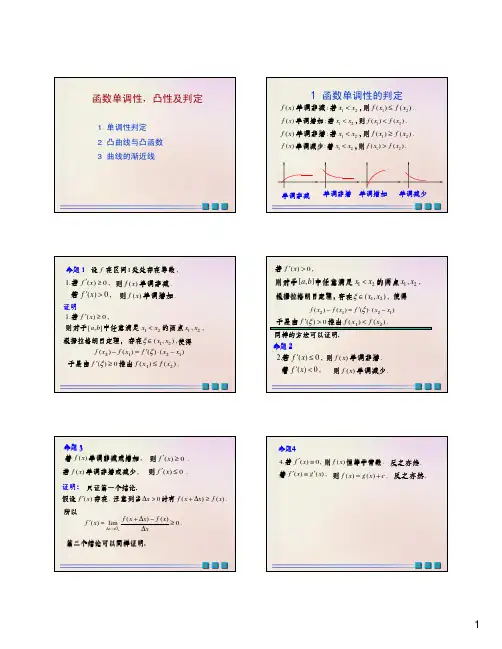
函数单调性,凸性及判定1 单调性判定2凸曲线与凸函数3曲线的渐近线1 函数单调性的判定1212():()().f x x x f x f x <≤单调非减若,则1212():()().f x x x f x f x <<单调增加若,则1212():()().f x x x f x f x <≥单调非增若,则1212():()().f x x x f x f x <>单调减少若,则单调非减单调非增单调增加单调减少命题1I ,f 设在区间处处存在导数1.()0,f x ′≥若()0,f x ′>若().f x 则单调非减().f x 则单调增加证明1.()0,f x ′≥若1212[,],,a b x x x x <则对于中任意满足的两点)()()()(1212x x f x f x f −⋅′=−ξ12(,),x x ξ∈存在使得12()0()().f f x f x ξ′≥≤于是由推出根据拉格朗日定理根据拉格朗日定理,,命题3(),f x 若单调非减或增加()0.f x ′≥则证明证明::0()()()lim0.x f x x f x f x x+∆→+∆−′=≥∆(),f x 若单调非增或减少()0.f x ′≤则第二个结论可以同样证明第二个结论可以同样证明..只证第一个结论只证第一个结论...)(存在假设x f ′.)()(0x f x x f x ≥∆+>∆时有注意到当所以命题命题444.()0,f x ′≡若()(),f x g x ′′≡若().f x 则恒等于常数.反之亦然()().f x g x c =+则.反之亦然x y tan =π0 ,2x <<求证当时有不等式:.tan 3 3x x x <+例133x x y +=证明;tan x x <首先证明第一个不等式首先证明第一个不等式..()tan f x x x =−令.)2π0(01sec )(2<<>−=′x x x f π()[0,).2f x 于是在单调增加(0)0f =由于,π(0,)()0.2f x >所以在有tan .x x >即xy =3π()tan (0).32x f x x x x =−−≤<令.)2π0(0tan 1sec )(2222<<>−=−−=′x x x x x x f 3tan .3x x x +<再证明π()[0,).2f x 于是在单调增加(0)0f =由于,π(0,)()0.2f x >所以在有21tan .3x x x >+即函数的凸性与曲线的凸性,,,,a b c d 观察同一区间上的四条曲线abcd,,a b 所表示的函数都单调减少,c d 表示的函数都单调增加,;但它们的形态很不相同这给与我们一个提示这给与我们一个提示::还需要考察函数在区间上的凸性还需要考察函数在区间上的凸性...但它们增加的规律差异很明显仅有单调性不足以精确地反映函数的变化规律仅有单调性不足以精确地反映函数的变化规律..函数下凸严格定义函数下凸严格定义::.,)(b x a x f y ≤≤=12[,]x x a b ∈如果对于任意两点,,12121()[()()]22x x f f x f x +<+都有.],[)(为下凸函数在则称b a x f a b)(x f y =12()2x x f +121[()()]2f x f x +1x 2x 定理定理11.)(存在导数在区间假设I x f 下凸的充分必要条件是在则I x f )(.)(单调增加在I x f ′证明:只证充分性只证充分性,,略去必要性证明.().f x I ′假设在单调增加)(2121x x x x I <,任取两点在区间)(21210x x x +=))(()()(01101x x f x f x f −′+=ξ根据拉格朗日定理得到20220()()()()f x f x f x x ξ′=+−),(011x x ∈ξ201(,)x x ξ∈))(()()(01101x x f x f x f −′+=ξ20220()()()()f x f x f x x ξ′=+−),(011x x ∈ξ201(,)x x ξ∈12021211()()2()[()()]()2f x f x f x f f x x ξξ′′+=+−⋅−21()()()f x f f ξξ′′′>单调增加推出于是120()()2()f x f x f x +>从而120()()().2f x f x f x +>下凸函数的几何意义下凸函数的图像的特点下凸函数的图像的特点::ab)(x f y =①弦在上弦在上,,弧在下弧在下..1x 2x 3x ②曲线在上曲线在上,,切线在下这两个结论的证明留给大家研究这两个结论的证明留给大家研究..定理定理22().f x I 假设在区间存在二阶导数()f x I 则在下凸的充分条件是()0.f x ′′>上凸函数定义上凸函数定义::12121()[()()]22x x f f x f x +>+定理3:()f x 上凸的充要条件:().f x ′单调减少().f x ′若存在定理定理44().f x I 假设在区间存在二阶导数()f x I 则在上凸的充分条件是()0.f x ′′<上凸函数的几何特征上凸函数的几何特征::2x 1x AB122x x +①弦在下弦在下,,弧在上弧在上..②弧在下弧在下,,切线在上切线在上..1x 2x 3x 4x )1(>=p x y p (1)q y x q =<xy ln =xy e =P >0 下凸下凸;;0<p <1 上凸上凸..:p x 幂函数(1)x a a >指数函数下凸;(1)x a a >对数函数上凸.xyπ−π;上凸,)π)12(,π2(:sin +=n n x y sin :((21)π,2π),.y x n n =−下凸x yx 拐点的必要条件拐点的必要条件::,的拐点是曲线假设)())(,(00x f y x f x P =,连续如果)(x f ′′0()0.f x ′′=则必有)2)(1(−−=x x x y )1(6−=′′x y (1)0y ′′=1,6(1)0,x y x ′′<=−<时上凸;1,6(1)0,.x y x ′′>=−>时下凸.)0,1(是拐点P 221e )(x x x f −=例研究单调性和凸性研究单调性和凸性..22112221()e e ()2x x f x x x −−′′=+⋅⋅−2211222()e e x x fx x−−′=−⋅2122e (1)x x −=−2122()[()][e (1)]x f x fx x −′′′′′==−2122e (3)x x x −=−2−4−24xyO221ex x y −=2122()e (1)x f x x −′=−研究单调性研究单调性...0)(:)1,(<′−−∞x f .)(单调减少x f (1,1):()0.f x ′−<().f x 单调增加(1):()0.f x ′+∞<,.)(单调减少x f 研究凸性研究凸性..(,3):()0.f x ′′−∞−<().f x 上凸(30):()0.f x ′′−>,().f x 下凸(0,3):()0.f x ′′<().f x 上凸2122()e(3)x f x x x −′′=−(3):()0.f x ′′+∞>,().f x 下凸拐点拐点::)3,3(23−−−e A 32(3,3)B e−)0,0(O 2−4−24xyO221ex x y −=自我评估题2302224.limtan xx ex x x−→−+−31−2csc5.lim(cos )xx x →12−016.lim(csc )x x x→+0自我评估题11.,??1y y y x′′′===+sin 2.x y x=3.()ln (0)f x x x x =>?d ?)1(1==′=x y y ??y y ′′′==2)1(sin cos )1(x x x x y +−+=′32)1(sin )12(cos )1(2x xx x x x y +−+++=′′(0)1y ′=2)0(=′′y 研究单调性和凸性研究单调性和凸性..O12−e xx x x 22ln )ln (−=′。

凸函数判定方法的研究凸函数是数学中一个非常重要且广泛应用的概念。
在优化问题、经济学、工程学等领域,凸函数都有着广泛的应用。
因此,研究凸函数判定方法是非常有意义的。
凸函数的定义是:若函数f 的定义域为凸集,并且对于所有的x1 和x2,以及任意的t∈[0,1],总有f(tx1+(1−t)x2)≤tf(x1)+(1−t)f(x2)成立,则f 称为凸函数。
也可以简单地理解为,凸函数的任意两点连线上的函数值,都小于等于连线上的两个端点对应的函数值之间的线性插值。
目前,已经有一些成熟的方法和定理可用于凸函数的判定。
下面将对其中比较常用的方法进行介绍。
一、一阶判定法一阶判定法是判定凸函数最简单、常用和基本的方法之一、其基本思想是利用函数的导数性质来判断函数是否为凸函数。
首先,对于凸函数而言,一阶导数必须是单调递增的。
也就是说,如果函数f在一些区间内的一阶导数是递增的,那么f就可以被判断为凸函数。
如果一阶导数是严格递增的,则f被称为严格凸函数。
其次,对于二次函数而言,如果它的二阶导数恒大于等于0,那么它也是凸函数。
也就是说,一阶导数是递增函数的充分必要条件是二阶导数为非负数。
二、二阶判定法二阶判定法是一种比一阶判定法更严格、更精确的方法,它使用函数的二阶导数来判断函数的凸性。
对于凸函数而言,其二阶导数必须是非负的。
也就是说,如果一个函数的二阶导数在定义域内都为非负数,那么该函数就是凸函数。
如果二阶导数严格大于零,则函数被称为严格凸函数。
三、线性规划判定法线性规划判定法是一种基于线性规划理论的凸函数判定方法。
其基本思路是将凸函数的判定问题转化为一个线性规划问题,然后利用线性规划的性质和算法来进行判定。
具体来说,设函数f的定义域为凸集D,对于所有的x∈D,有f′(x)为连续函数。
如果对于所有的x∈D,存在一个c∈D,使得f′(c)=0,并且对于所有的x∈D,有f′(x)≥0,则函数f是凸函数。
反之,如果对于所有的x∈D,有f′(x)≤0,则函数f是凹函数。

函数凸性定义的等价性及其判别方法研究吴文虎(陕理工数学与计算科学学院数学与应用数学 092班,陕西 汉中 723000)指导教师:雍龙泉【摘要】凸分析是数学中相对年轻的一个分支。
凸函数作为凸分析的主要研究对象,在凸分析中占有重要地位,其定义、性质经常作为解决数学规划论、对策论、数理经济学、逼近论、变分学、最优控制理论这些方面的问题的工具被加以使用。
本文深入地讨论了凸函数的几种不同定义的等价性,判别方法及凸函数的应用。
首先给出了凸函数的六个不同方式的定义。
然后探究出定义之间的关系,得出定义的等价性,在前三个定义中下(上)凸函数的本质是连接函数图形上任意两点的线段,处处都不在函数图形的下方(或上方)。
后三个定义中下(上)凸函数的本质是左差商不大于(不小于)右差商,左右差商当自变量差分减小时是不减(不增)的。
然后给出凸函数的判别方法的研究及其证明。
最后举例说明凸函数的相关结论在不等式的证明、验证级数的收敛性等方面的应用。
【关键词】 凸函数;等价定义;判定方法1、引言凸分析,或称凸集和凸函数理论,是数学中相对年轻的一个分支,在本世纪三十年代才出现比较系统的研究凸集的著作,40至50年代,特别是在优化领域发现了凸集的许多应用以后,更进一步促进了这一理论的发展,随着数学规划论、对策论、数理经济学、逼近论、变分学、最优控制理论等学科发展的需要,凸分析日益受到大家的重视,60年代后期出现凸分析的奠基之作,即R.T.Rockafellar 的“Convex Analysis”,无穷维空间中凸分析的理论在这一时期也得到了充分的发展,到现在,凸分析已经成了解决数学规划论、对策论、数理经济学、逼近论、变分学、最优控制理论这方面问题的主要手段。
凸分析包括凸集、凸函数、凸锥、赋范空间的凸性、正解理论等方面的内容,其基本研究对象是凸集和凸函数,基本工具是凸集分离定理,而这些概念和定理都可以纯代数的研究,即在一个不引入拓扑的线性空间中来研究。

函数的凹凸性与拐点的判定在微积分中,函数的凹凸性与拐点是非常重要的概念。
凹凸性描述了函数曲线的弯曲情况,而拐点则表示曲线的方向发生改变的点。
凹凸性和拐点的判定对于函数的研究和应用具有重要作用。
本文将介绍函数凹凸性和拐点的概念,并讨论如何判定和应用。
一、函数的凹凸性函数的凹凸性是指函数曲线的弯曲情况。
我们可以通过函数的二阶导数来判断函数的凹凸性。
1. 定义设函数f(x)在区间I上具有二阶导数,如果对于任意x1和x2∈I,有f''(x)>0,则函数f(x)在区间I上是凹函数;如果对于任意x1和x2∈I,有f''(x)<0,则函数f(x)在区间I上是凸函数。
2. 凹凸点根据函数的凹凸性质,我们可以定义凹凸点。
若对于函数f(x)的定义域I上的某一点x0,存在一个区间(x0-δ,x0+δ),在该区间内f(x)是凹函数,那么称点(x0,f(x0))是函数f(x)的一个凹点;若在区间(x0-δ,x0+δ)内f(x)是凸函数,则称点(x0,f(x0))是函数f(x)的一个凸点。
二、拐点的判定拐点表示函数曲线的方向发生改变的点。
我们可以通过函数的二阶导数来判断拐点。
1. 定义设函数f(x)在区间I上具有二阶导数。
如果在某一点x0∈I处,f''(x0)=0,并且f''(x0-)和f''(x0+)的符号相反,则称点(x0,f(x0))是函数f(x)的一个拐点。
2. 拐点的性质拐点具有以下性质:- 在拐点处,函数的凹凸性发生改变,由凸转为凹或由凹转为凸。
- 拐点不一定存在,只有当函数曲线的凹凸性发生改变时,才会有拐点。
- 如果函数曲线有k个拐点,那么至多有k+1个不同的凹凸区间。
三、判定和应用判定函数的凹凸性和拐点的方法可以通过以下步骤进行。
1. 求导数首先,求出函数f(x)的一阶和二阶导数f'(x)和f''(x)。

凸函数判定方法的研究鸡冠山九年一贯制学校张岩2013年12月15日目录摘要 (ii)关键词 (ii)Abstract (ii)Key words (ii)前言 (iii)一、凸函数的基本理论 (1)1、预备知识 (1)2、凸函数的概念及性质 (2)二、凸函数的判定方法 (4)(一)一元函数凸性的判定方法 (4)1、利用作图判断函数凸性 (4)2、其它判定方法 (5)(二)多元函数凸性的判定方法 (8)1、多元凸函数的有关概念 (8)2、多元函数凸性的判定方法 (9)三、凸函数几个其他判定方法 (12)四、总结 (14)参考文献 (14)致谢 (15)凸函数判定方法的研究摘要:凸函数是一类非常重要的函数,借助它的凸性可以科学准确地描述函数图像,而且可以用于不等式的证明。
同时,凸函数也是优化问题中重要的研究对象,研究的内容非常丰富,研究的结果已在许多领域得到广泛的应用,因此凸函数及其性质以及凸性判定的充要条件的研究就显得尤为重要。
本文首先给出了凸函数的一些基本概念和结论,然后针对一元和多元函数,对凸函数的判定做了研究和讨论,本文最后也给出几种新的判定凸函数的方法。
关键词:凸函数;梯度;Hesse 矩阵;泰勒定理Abstract: Convex function is a kind of very important functions, with the help of its convexity we can accurately describe the graph of functions and it can also be used to prove the inequalities. As the significant object in optimization problems, the contents about convex functions we study are very abundant, the results obtained so far has been applied to many fields. Therefore, the topic we concern about is deserved to be discussed. In this paper, we firstly present some basic definitions and properties of convex functions, then aiming at the univariate function and multi-variable functions we give several criterions for determining the convexity of functions. Finally, some new principles are also given.Key words:Convex function; Gradient; Hesse matrix; Taylor Theorem前言提起凸函数,人们都会想起它的许多良好性质和在数学中的重要作用。

如何判断一个函数是否是凸的要判断一个函数是否是凸的,我们需要了解什么是凸函数以及凸函数的性质。
在数学中,一个函数被称为凸函数,如果对于任意两个取值在定义域上的点,连接这两个点的线段上的函数值不大于这两个点各自的函数值之间的线性插值。
简而言之,凸函数的图像在两点之间的部分,在这两点之间的连线上。
下面详细介绍凸函数的定义和相关性质,以及判断函数是否是凸函数的方法。
一、凸函数的定义:给定一个定义域为D的函数f,如果对于D上的任意两个点x1和x2,以及任意实数λ(0≤λ≤1),都满足如下条件:f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2)则函数f被称为凸函数。
这个定义可以理解为,对于连接函数f上任意两点连线上的点x,函数f(x)的取值都不会超过连接这两个点的线段上函数值的线性插值。
如果函数f满足这个定义,则称f为凸函数。
二、凸函数的性质:1.凸函数的图像上的任意两个点之间的连线都在函数图像的上方或者是函数图像本身。
这可以由凸函数的定义推导得出。
2.凡是非空凸集的非空凸组合,对于凸函数f都有f(凸组合)≤凸组合的f值之和。
三、判断函数是否是凸的方法:1.一阶导数法:对于定义在实数集上的函数f,如果f在定义域上是可导的,那么对于凸函数来说,它的一阶导数是递增的。
我们可以通过计算函数的一阶导数来判断其递增性。
如果一阶导数始终大于等于零,则函数是凸的;如果一阶导数始终大于零,则函数是严格凸的。
2.二阶导数法:对于定义在实数集上的函数f,如果f在定义域上是二阶可导的,并且其二阶导数大于等于零,那么函数f是凸的;如果二阶导数大于零,则函数是严格凸的。
通过计算函数的二阶导数来判断其凸性。
3.利用判别凸函数的性质:通过判断函数图像上的连线是否在函数上方,可以直观地判断函数是否是凸的。
四、凸函数的常见类型:1. 线性函数:f(x) = ax + b,其中a和b为实数。
线性函数是凸函数也是凹函数。
2.常数函数:f(x)=c,其中c为实数。


多元凸函数的判定1 引言凸函数是一类基本函数,具有非常好的分析学性质,在极值研究、不等式证明、数学规划、逼近论、变分学、最优控制理论、对策论等领域有着广泛的应用. 人们对一元凸函数性质和判定方法已经有了丰富的研究,但随着凸函数应用范围的不断扩展,多元凸函数越来越多的被研究. 一元函数凸性的判定方法也被推广到多元函数,文献[4]将凸函数与导函数之间的关系推广,给出了用梯度判定多元函数凸性的方法,文献[5]将凸函数与二阶导数之间的关系推广,给出了用黑塞矩阵判定多元函数凸性的方法. 而多元函数的梯度与黑塞矩阵在计算中往往比较繁琐,本文将着力研究多元函数凸性判定方法的改进,使凸函数判定的计算更加简洁,应用更加方便. 2 定义及引理本节主要介绍本文用到的定义及引理.定义2.1[2] 设n R D ⊂,如果D 中的任意两点的连线也在D 内,则称D 为n R 中的凸集. 即对任意21,P P ,数)1,0(∈λ,总有D P P ∈-+21)1(λλ.定义 2.2[1] 设n R D ⊂为非空凸集,f 为定义在D 上的函数,若对任意)1,0(,,21∈∈λD P P ,总有)()1()())1((2121P f P f P P f λλλλ-+≤-+, (1)则称f 为D 上的凸函数. 反之,如果总有)()1()())1((2121P f P f P P f λλλλ-+≥-+, (2)则f 为D 上的凹函数.若上述(1)、(2)中的不等式改为严格不等式,则相应的函数称为严格凸函数和严格凹函数.定义]2[3.2 )(P f 是定义在n R D ⊂上的多元函数,若在点),,,(210n x x x P ⋅⋅⋅存在对所有自变量的偏导数,则称向量))(,),(),((00021P f P f P f n x x x ⋅⋅⋅为函数)(P f 在点0P 的梯度,记作)).(,),(),(()()(0000021P f P f P f P gradf P f n x x x ⋅⋅⋅==∇定义]2[4.2 )(P f 是定义在n R D ⊂上的多元函数,且在点),,,(210n x x x P ⋅⋅⋅具有二阶连续偏导数,记⎪⎪⎪⎪⎪⎭⎫⎝⎛⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=)()()()()()()()()()(0000000000212221212111P f P f P f P f P f P f P f P f P f P H n n n n n n x x x x x x x x x x x x x x x x x x f 它称为)(P f 在0P 的黑赛矩阵.引理2.1[1] (泰勒定理) 若函数f 在],[b a 上存在直至n 阶的连续导函数,在),(b a 上存在)1(+n 阶导函数,则对任意给定得],[,0b a x x ∈,至少存在一点),(b a ∈ξ,使得.)()!1()()(!)()(!2)())(()()(10)1(00)(200000++-++-+⋅⋅⋅+-''+-'+=n n n n x x n f x x n x f x x x f x x x f x f x f ξ3 已有结果定理]1[1.3 f 为I 上的凸函数的充要条件是:对于I 上的任意三点321x x x <<,总有.)()()()(23231212x x x f x f x x x f x f --≤--定理]1[2.3 设f 为区间I 上的二阶可导函数,则在I 上f 为凸(凹)函数的充要条件是)0)((0)(≤''≥''x f x f ,I x ∈.定理]4[3.3 设)(P f 为凸集n R D ⊂内可微函数,则)(P f 为D 内的凸函数的充要条件是:对任意D P ∈,D P P ∈∆+,则P P f P f P P f T ∆∇+≥∆+)()()(.定理]5[4.3 设)(P f 是定义在非空开集n R D ⊂的二次可微函数,则)(P f 是凸函数的充要条件是在任意点D P ∈处)(P f 的黑赛矩阵半正定.定理]5[5.3 设)(P f 是定义在非空开集n R D ⊂的二次可微函数,若)(P f 的黑赛矩阵在任意点D P 处正定,则)(P f 是严格凸函数.。
§ 5 函数的凸性与拐点一. 凸性的定义及判定:1. 凸性的定义:由直观引入. 强调曲线弯曲方向与上升方向的区别.定义1 设函数)(x f 在区间I 上连续. 若对∈∀21,x x I 和)1,0(∈λ恒有)()1()())1((2121x f x f x x f λλλλ-+≤-+则称曲线 )(x f y = 在区间I 的凸函数, 反之, 如果总有)()1()())1((2121x f x f x x f λλλλ-+≤-+则称曲线 )(x f y = 在区间I 的凹函数.若在上式中, 当21x x ≠时, 有严格不等号成立, 则称曲线)(x f y =在区间],[b a 上是严格凸(或严格凹)的.引理 )(x f y =为区间I 上的凸函数的充要条件是:对I 上任意三点: 321x x x << , 总有23231212)()()()(x x x f x f x x x f x f --≤-- 定理6.13 设函数)(x f 在区间I 上可导, 则下面条件等价:(i) 为I 上凸函数(ii) 为I 上的增函数(iii) 对I 上的任意两点21,x x 有))(()()(12112x x x f x f x f -'+≥2. 利用二阶导数判断曲线的凸向:Th 6.14 设函数)(x f 在区间),(b a 内存在二阶导数, 则在),(b a 内⑴ )( ,0)(x f x f ⇒<'' 在 ),(b a 内严格上凸;⑵ )( ,0)(x f x f ⇒>'' 在 ),(b a 内严格下凸.证法一 ( 用Taylor 公式 ) 对),,(,21b a x x ∈∀ 设2210x x x +=, 把)(x f 在点0x 展开成具Lagrange 型余项的Taylor 公式, 有,)(2)())(()()(201101001x x f x x x f x f x f -''+-'+=ξ 202202002)(2)())(()()(x x f x x x f x f x f -''+-'+=ξ. 其中 1ξ 和 2ξ在 1x 与 2x 之间. 注意到 )(0201x x x x --=-, 就有 []20222011021))(())((21)(2)()(x x f x x f x f x f x f -''+-''+=+ξξ, 于是, 若有⇒<'' ,0)(x f 上式中[])(2)()( ,0021x f x f x f <+⇒< ,即 )(x f 严格上凸.若有⇒>'' ,0)(x f 上式中[])(2)()( ,0021x f x f x f >+⇒> ,即)(x f 严格下凸.证法二 ( 利用Lagrange 中值定理. ) 若,0)(>''x f 则有)(x f '↗↗.不妨设 21x x <, 并设 2210x x x +=, 分别在区间],[01x x 和],[20x x 上应用Lagrange 中值定理, 有))(()()( ),,(10110011x x f x f x f x x -'=-∍∈∃ξξ,))(()()( ),,(02202202x x f x f x f x x -'=-∍∈∃ξξ.有),()( ,2122011ξξξξf f x x x '<'⇒<<<< 又由 00210>-=-x x x x ,⇒))((101x x f -'ξ<))((022x x f -'ξ, ⇒)()()()(0210x f x f x f x f -<-, 即 ⎪⎭⎫⎝⎛+=>+22)(2)()(21021x x f x f x f x f , )(x f 严格下凸. 可类证0)(<''x f 的情况.3. 凸区间的分离: )(x f ''的正、负值区间分别对应函数)(x f 的下凸和上凸区间.二. 曲线的拐点: 拐点的定义.例1 确定函数2)(x xe x f -=的上凸、下凸区间和拐点.解 f 的定义域为), , (∞+∞-),21()(22x e x f x -='- 2)32(2)(2x e x x x f --=''. 令0)(=''x f , 解得 23 , 0 , 23321==-=x x x . 在区间) , 23 ( , ) 23 , 0 ( , ) 0 , 23 ( , ) 23 , (∞+--∞-内f '' 的符号依次为 +-+- , , , , ⇒. 拐点为: .23 , 23 , ) 0 , 0 ( , 23 , 232323⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---e e倘若注意到本题中的)(x f 是奇函数, 可使解答更为简捷.Jensen 不等式及其应用:Jensen 不等式: 设函数)(x f 为区间],[b a 上的凸函数, 则对任意 ],[b a x i ∈, 1,,1,01==>∑=ni i i i λλ , 有Jensen 不等式:)()(11i n i ni i i i x f x f ∑∑==≤λλ,且等号当且仅当n x x x === 21时成立.证 令∑==nk k x n x 101, 把)(k x f 表为点0x 处具二阶Lagrange 型余项的Taylor 公式,仿前述定理的证明,注意∑==-n k k x x10,0)( 即得所证.例2 证明: 对,,R ∈∀y x 有不等式 )(212y x yx e e e +≤+. 例3 证明均值不等式: 对+∈∀R n a a a ,,,21 , 有均值不等式n a a a n11121+++ n a a a a a a n n n +++≤≤ 2121 . 证 先证不等式na a a a a a n n n +++≤ 2121 . 取x x f ln )(=. )(x f 在) , 0 (∞+内严格上凸, 由Jensen 不等式, 有∑∑∑∑∏=====⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛≤==n k n k k n k k k n k k n n k k x n x n f x f n x n x 111111ln 1)(1ln 1ln . 由)(x f ↗↗ ⇒ na a a a a a n n n +++≤ 2121 . 对+∈R na a a 1,,1,121 用上述已证结果, 即得均值不等式的左半端. 例4 证明: 对R ∈∀n x x x ,,,21 , 有不等式 nx x x n x x x n n 2222121 +++≤+++ . ( 平方根平均值 ) 例5 设6=++z y x ,证明 12222≥++z y x .解 取2)(x x f =, 应用Jensen 不等式.例6 在⊿ABC 中, 求证 233sin sin sin ≤++C B A . 解 考虑函数x x x f x x x f sin . 0 , 0 sin .0 ,sin )(⇒<<-=''≤≤=ππ在 区间) , 0 (π内凹, 由Jensen 不等式, 有233sin 33)()()(3sinC sinB sinA ==⎪⎭⎫ ⎝⎛++≤++=++∴πC B A f C f B f A f . 233sinC sinB sinA ≤++⇒. 例7 已知1 ,,,=++∈+c b a c b a R . 求证 6737373333≤+++++c b a .解 考虑函数3)(x x f =, )(x f 在) , 0 (∞+内严格上凸. 由Jensen 不等式, 有 ≤+++++=+++++3)73()73()73(3737373333c f b f a f c b a 28)8()7(37373733===+++=⎪⎭⎫ ⎝⎛+++++≤f c b a f c b a f . ⇒ 6737373333≤+++++c b a .例8 已知 .2 , 0 , 033≤+>>βαβα 求证 2≤+βα.( 解 函数3)(x x f =在) , 0 (∞+内严格下凸. 由Jensen 不等式, 有=+≤⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=+2)()(228)(33βαβαβαβαf f f ⇒=≤+ ,122233βα 2 , 8)(3≤+⇒≤+βαβα.)。
凸函数知识点总结一、基本概念1.1 凸集在讨论凸函数之前,首先需要了解凸集的概念。
凸集是指对于集合中的任意两个点,连接这两个点的线段仍然完全包含在这个集合中。
即对于集合中的任意两个点a和b,线段[a,b]上的所有点都属于该集合。
在数学上,给定一个集合S,如果对于任意的x、y∈S和0≤t≤1,tx+(1−t)y∈S,就称S是凸集。
1.2 凸函数在了解了凸集的概念之后,可以进一步理解凸函数。
在一个实数集上,如果一个函数f(x)满足如下性质:对于任意的x1和x2以及0≤t≤1,有f(tx1+(1−t)x2)≤tf(x1)+(1−t)f(x2),那么函数f(x)就是凸函数。
也就是说,对于函数上的任意两点x1和x2,连接这两个点的线段上的所有点(x)对应的函数值f(x),都位于连接这两个点的线段上。
可以用一条直线来连接这两点,并且在这条直线的下方。
1.3 凸函数的图形在笛卡尔坐标系中,凸函数的图形呈现出一种特殊的形状。
它们通常是上凸的(在图像的上方),或者是下凸的(在图像的下方)。
这种凸性质是凸函数的重要特征,也是区分它们与其他函数的重要标志。
二、性质凸函数有许多重要的性质,这些性质对于理解和应用凸函数都非常重要。
下面列举了一些凸函数的一些重要性质:2.1 一阶导数的性质首先,凸函数在其定义域上是连续且可导的。
其次,凸函数的导数是递增的。
也就是说,对于凸函数f(x),在它的定义域内,如果x1<x2,那么f'(x1)≤f'(x2)。
2.2 二阶导数的性质在凸函数的定义域内,凸函数的二阶导数必须是非负的。
也就是说,如果f(x)是凸函数,那么它的二阶导数f''(x)≥0。
2.3 凸函数的上确界如果一个凸函数在其定义域上是有上界的,那么它的上确界也存在,并且是有限的。
这是因为凸函数的定义保证了它在定义域上是有界的,并且在定义域上是递增的。
因此,上确界也必然存在。
2.4 凸函数的极值凸函数的极小值点是唯一的,而且在极小值点的函数值是整个定义域上的最小值。
函数凹凸性判定在微积分中,研究函数的凹凸性是很重要的。
凹凸性指的是函数图像在特定区间上的弯曲程度,它与函数的二阶导数有着密切的关系。
在本文中,我们将讨论如何判定函数的凹凸性。
凹凸性的定义很简单:如果函数的图像在给定区间内呈现向上的弯曲形状,那么该函数在该区间上是凹函数;如果函数的图像呈现向下的形状,那么该函数在该区间上是凸函数。
一阶导数和二阶导数在讨论凹凸性之前,我们先回顾一下导数的概念。
假设有一个函数 [f(x)],它在某个区间 [I] 上可导。
那么,函数在该区间上的导数[f’(x)] 描述了函数曲线的斜率。
一阶导数描述了函数曲线的变化速率。
如果导数大于零,表示函数在该点的斜率为正,即函数曲线向上倾斜;如果导数小于零,则函数曲线向下倾斜;如果导数等于零,则函数曲线在该点上是水平的。
二阶导数描述了一阶导数的变化。
如果函数的二阶导数大于零,表示函数的一阶导数在该点上是递增的,即函数的曲线向上弯曲;如果函数的二阶导数小于零,则表示函数的一阶导数在该点上是递减的,即函数的曲线向下弯曲;如果二阶导数等于零,则表示函数的曲线是水平的。
判定凹函数和凸函数根据一阶导数和二阶导数的概念,我们可以得到以下结论来判定函数的凹凸性:•若函数在某个区间上的二阶导数始终大于零,那么该函数在该区间上是凸函数;•若函数在某个区间上的二阶导数始终小于零,那么该函数在该区间上是凹函数。
根据这个结论,我们可以设计一个简单的算法来判定函数的凹凸性。
下面我们使用 Python 代码来实现这个算法:```python def is_convex(f, a, b): dx = 0.0001 # 步长 x = a while x <= b:f_prime_prime = (f(x + dx) - 2 * f(x) + f(x - dx)) / (dx ** 2) if f_prime_prime < 0:return False x += dx return True示例函数 f(x) = x^2def f(x): return x ** 2a = -1b = 1 if is_convex(f, a, b): print(。
凸函数的性质:(1)设)(),(21x x f f 是凸集nR⊂Ω上的凸函数,则)()(21x x f f +也是Ω上的凸函数; (2)设)(x f 是凸集nR⊂Ω上的凸函数,则对任意常数0>c,函数)(x cf也是凸函数; (3)设)(x f 是凸集nR⊂Ω上的凸函数,则对任意实数c,水平集{}c f ≤Ω∈)(,x x x 是凸集。
(4)设Ω是内部非空的凸集,)(x f是定义在Ω上的凸函数,则)(x f 在Ω的内部连续。
凸函数的判定条件当函数一阶或二阶可微时,除了可以根据定义来判断其是否是凸函数外,更常用的方法是如下的判别条件:定理1-2 定义在凸集nR⊂Ω上的可微函数)(x f 为凸函数的充要条件是:对于任意Ω∈y x ,都有)()()()(x y x x y -∇+≥Tf f f (1-23)定理1-2的几何意义:设)(x f 是一元凸函数,21,x x 是两个不同点,则))(()()(12112x x x f x f x f -'+≥即凸函数的图像上任一点切线上的纵坐标总不大于曲线在该点的纵坐标,见图1-4,反之亦然。
图1-4 凸函数的几何意义只要将定理1-2中(1-23)式的“≥”改为“>”,就可得到严格凸函数的充要条件。
定理1-3(凸函数的二阶充要条件) 设nR⊂Ω为含有内点的凸集,)(x f在Ω上二次可微,则)(x f 为Ω上凸函数的充要条件是:)(x f 的Hesse 矩阵)(2x f ∇在整个Ω上半正定。
特别地,当1=n时,)(x f 的Hesse 矩阵)()(2x f x f ''=∇,则该定理为:若)(x f 具有二阶连续导数,则)(x f 为凸函数的充要条件是:0)(≥''x f,其中),(b a x ∈。
定理1-4(严格凸函数的二阶充分条件) 设nR⊂Ω为非空开凸集,)(x f在Ω上二次可微,若)(x f 的Hesse 矩阵)(2x f ∇在Ω上处处正定,则)(x f 为Ω上的严格凸函数。
凸函数判定方法的研究鸡冠山九年一贯制学校张岩2013年12月15日目录摘要 (ii)关键词 (ii)Abstract (ii)Key words (ii)前言 (iii)一、凸函数的基本理论 (1)1、预备知识 (1)2、凸函数的概念及性质 (2)二、凸函数的判定方法 (4)(一)一元函数凸性的判定方法 (4)1、利用作图判断函数凸性 (4)2、其它判定方法 (5)(二)多元函数凸性的判定方法 (8)1、多元凸函数的有关概念 (8)2、多元函数凸性的判定方法 (9)三、凸函数几个其他判定方法 (12)四、总结 (14)参考文献 (14)致谢 (15)凸函数判定方法的研究摘要:凸函数是一类非常重要的函数,借助它的凸性可以科学准确地描述函数图像,而且可以用于不等式的证明。
同时,凸函数也是优化问题中重要的研究对象,研究的内容非常丰富,研究的结果已在许多领域得到广泛的应用,因此凸函数及其性质以及凸性判定的充要条件的研究就显得尤为重要。
本文首先给出了凸函数的一些基本概念和结论,然后针对一元和多元函数,对凸函数的判定做了研究和讨论,本文最后也给出几种新的判定凸函数的方法。
关键词:凸函数;梯度;Hesse 矩阵;泰勒定理Abstract: Convex function is a kind of very important functions, with the help of its convexity we can accurately describe the graph of functions and it can also be used to prove the inequalities. As the significant object in optimization problems, the contents about convex functions we study are very abundant, the results obtained so far has been applied to many fields. Therefore, the topic we concern about is deserved to be discussed. In this paper, we firstly present some basic definitions and properties of convex functions, then aiming at the univariate function and multi-variable functions we give several criterions for determining the convexity of functions. Finally, some new principles are also given.Key words:Convex function; Gradient; Hesse matrix; Taylor Theorem前言提起凸函数,人们都会想起它的许多良好性质和在数学中的重要作用。
的确,凸函数是一个十分重要的数学概念,它在纯粹数学和应用数学的众多领域中具有广泛的应用。
在数学分析和高等数学教材中,函数的凹性和凸性一直都占据着重要的位置,关于这两个性质的考查也常常见诸于练习和考试中.凸函数是一类非常重要的函数,广泛应用于数学规划,控制论等领域,函数凸性是数学分析专攻的一个重要概念,它在判定函数的极值、研究函数的图象以及证明不等式诸方面都有广泛的应用。
凸分析作为数学的一个比较年轻的分支,是在50年代以后随着数学规划,最优控制理论、数理经济学等应用数学学科的兴起而发展起来的。
运筹学是在二十世纪四十年代才开始兴起的一门分支。
运筹学的创始人定义运筹学是:“管理系统的人为了获得关于系统运行的最优解而必须使用的一种科学方法。
”它使用许多数学工具(包括概率统计、数理分析、线性代数等)和逻辑判断方法,来研究系统中的人、财、物的组织管理、筹划调度等问题,以期发挥最大的效益。
随着科学技术和生产的发展,运筹学已渗入很多领域里,发挥了越来越重要的作用。
但是,凸分析的局限性也是很明显的,实际问题中的大量函数是非凸的,因此,各种广义凸函数的定义相继出现,特别是近年来,“非凸分析”或更一般的“非光滑分析”已成为引人注目的热门课题,它们是凸分析的拓广和发展。
本文主要从凸函数出发给出凸函数的一些简单性质及一些重要的性质,然后给出了凸函数的几个等价定义并加以说明,然后利用函数图象判定函数的凸性,接下来给出了一些一元函数的判定方法并结合实例给出了判定函数凸性的一些等价条件,接着给出多元函数的判定方法及其应用,最后,又介绍了判定函数凸性的几个其他的方法。
一、凸函数的基本理论(一)预备知识1.梯度:若n 元函数()f x 对自变量12(,,,)T n x x x x =…的各分量i x 的偏导数()if x x ∂∂(1,2,)i n =…都存在,则称函数()f x 在x 处一阶可导,并称向量 12()()()()(,)Tnf x f x f x f x x x x ∂∂∂∇=∂∂∂,..., 为函数()f x 在x 处的梯度或一阶导数。
2 . Hesse 矩阵:若n 元函数()f x 具有二阶偏导数,即2()(,1,2,)i j f x i j n x x ∂=∂∂…,都存在,则称矩阵2221112122222122222212()()()()()()()()()()n n n n n n f x f x f x x x x x x x f x f x f x f x x x x x x x f x f x f x x x x x x x ⎛⎫∂∂∂⎪∂∂∂∂∂∂ ⎪ ⎪∂∂∂⎪∇=∂∂∂∂∂∂ ⎪ ⎪⎪ ⎪∂∂∂⎪∂∂∂∂∂∂⎝⎭┅┅┇┇┇┅为()f x 在x 处的Hesse 矩阵(海色矩阵)。
3. 泰勒展式(1)一阶泰勒展式:设()f x 在点_x 处具有一阶连续偏导,则()f x 在点_x 处的泰勒展开式____()()()()()f x f x f x x x x x ο=+∇-+-其中_()x x ο-为变量_x x -的高阶无穷小量_()x x →,或者__()()()()Tf x f x f x x ξ=+∇-,其中__()(01)x x x ξθθ=+-<<。
(2)二阶泰勒展式:设()f x 在点_x 处二阶连续可微(或具有二阶连续偏导数),则()f x 在点_x 处的二阶泰勒展开式为2_______21()()()()()()()()2T T f x f x f x x x x x f x x x x x ο=+∇-+-∇-+-或者 _____21()()()()()()()2TT f x f x f x x x x x f x x ξ=+∇-+-∇-,其中 __()(01)x x x ξθθ=+-<<。
(二)凸函数的概念及性质定义 1.1 设函数()f x 在区间I 上有定义, 若12,x x I ∀∈,总有()()()121211()22f x x f x f x ⎛⎫+≤+ ⎪⎝⎭ (1.1)则称()f x 为I 上的凸函数. 若在定义 1.1中当12x x ≠且不等式严格成立, 则称()f x 为I 上的严格凸函数.定义 1.2 设()f x 为定义在区间I 上的函数, 若对I 上的任意两点12,x x 和任意的()0,1λ∈总有()()1222(1)()1()f x x f x f x λλλλ+-≤+- (1.2)则称()f x 为I 上的凸函数.若(1.2)改为严格不等式,则称()f x 为严恪凸函数 定义 1.3 设函数()f x 在区间I 上有定义,若()12,,2n x x x I n ∀∈≥…,,总有()()()1212+n n f x f x f x x x x f n n +++++⎛⎫≤⎪⎝⎭…… (1.3) 则称()f x 为I 上的凸函数.1.凸函数的一些基本性质(1)若()x f 1、()x f 2均为[]b a ,上的凸函数,则()()x f x f 21+也是[]b a ,上的凸函数。
(2)设()x f 为[]b a ,上的凸函数,k 为正常数,则()x kf 也为[]b a ,上的凸函数。
(3)设()x f u =为[]b a ,上的凸函数,()u g 在[]b a ,上单调递增,且也为[]b a ,上的凸函数,则复合函数()()x f g 也是[]b a ,上的凸函数。
(4)若()x f u =是奇函数,且当0≥x 时,()x f u =是凸函数,则当0≤x 时,()x f u =是凹函数。
(5)若()x f u =是偶函数,且当0≥x 时,()x f u =是凸函数,则当0≥x 时,()x f u =是凸函数。
(6)若()x f y =是[]b a ,上的连续递增的凸函数,则()y f x 1-=是递增的凹函数。
(7)若()x f y =是定义在区间()b a ,上的凸函数,则()x f y =在()b a ,上连续。
(8)若()x f y =是()+∞∞-,上的凸函数且不恒为常数,则存在一点c 使得()x f y =在()c ,∞-上递减,在()+∞,c 上递增。
2.凸函数的一些重要性质性质1.1 设函数()f x 在I 上连续,若()f x 是I 上Jensen 意义下的凸函数,则12,x x I ∀∈及[]0,1λ∈都有(1.2)成立。
性质 1.2 (性质1的逆命题)设()f x 是定义在区间I 上的, 若对12,x x I ∀∈ ,[]0,1λ∈都有()()1222(1)()1()f x x f x f x λλλλ+-≤+-,则()f x 在I 内连续。
性质 1.3 若()f x 在区间I 上连续,且满足 ()()()21122121x x x x f x f x f x x x x x --≤+-- 其中12,x x I ∈,则()f x 是I 上的凸函数。
性质 1.4 若()f x 是闭区间[a,b]上有界的凸函数,()f x 在[a,b]内必连续。
性质 1.5 若函数()f x 是区间I 上的连续凸函数, 则有1) 函数()f x 在I 内处处存在左、右导数()'f x -与()'f x + , 且()()''f x f x -+≤; 2) ()'f x -与()'f x +都是x 的不减函数.二、凸函数的判定方法(一)一元函数凸性的判定方法1.利用作图判断函数凸性x 3x 2x 1B CAO图1-1上图是一个凸函数()f x 的几何图像,其中12(1)x x x λλ=+-,1()A f x =,2()A f x =,(1)C A B λλ=+-。