凹凸函数的判定方法

02 函数凹凸的几何意义
凹函数的几何意义
凹函数图像呈下凹状，即对于函数图 像上的任意两点A和B，如果A、B两 点连线的中点始终位于A、B连线的下 方，则该函数为凹函数。
在几何意义上，凹函数具有一个明显 的特征，即函数图像上任意两点的连 线的斜率始终小于或等于该点处的函 数导数。
凸函数的几何意义
通过分析函数的凹凸性，我们可以确定函数的拐点，从而更好地理解函数 的性质，为求解最优化问题提供指导。
在求解无约束最优化问题时，可以利用函数凹凸性选择合适的算法，如梯 度下降法、牛顿法等，以提高求解效率。
在经济学中的应用
函数凹凸性在经济学中也有 广泛应用，它可以帮助我们 理解经济现象和预测经济行
为。
函数凹凸的定义
目录
• 函数凹凸的基本概念 • 函数凹凸的几何意义 • 函数凹凸的判定方法 • 函数凹凸的应用 • 函数凹凸的反例 • 函数凹凸的扩展知识
01 函数凹凸的基本概念
凹函数
01
凹函数是指函数图形在任意两点 之间总是位于这两点连线的下方， 即对于定义域内的任意x1和x2， 都有 f((x1+x2)/2)≥f(x1)+f(x2)/2。
03
在计算机科学中，函数凹凸性可以帮助我们设计更有效的算法和数据 结构，如动态规划、图算法等。
04
在生物学中，函数凹凸性可以帮助我们理解生物系统的复杂性和行为， 如生态学、生物化学反应等。
05 函数凹凸的反例
凹函数的反例
总结词
凹函数的反例是指函数图像呈现下凹形状的反例。
详细描述
凹函数的反例通常是指那些在一定区间内，函数值随着自变量的增加而减少的函数。例如，二次函数 $f(x) = x^2$在区间$(-infty, 0)$内是一个凹函数的反例，因为在这个区间内，函数值随着$x$的增加 而减少。

连续曲线 y ? f ( x) 的拐点.
y
y ? x4
例如 ,
o
x
(2) 若 f ??( x0 ) 不存在 ,点 ( x0 , f ( x0 )) 也可能
是连续曲线 y ? f ( x ) 的拐点 .
y
例如 ,
o
25x
注意 改变凹凸性的点只可能是二阶导数为零及二阶 导数不存在的点 .
判断曲线的凹凸性和拐点的步骤：
x2
?
2,
3
对应
y1
(0,1)
(
2
3
,
11
27
)
?
1,
y2
?
2
11 27
3) 列表判别
3
x (?? ,0)
0
(0,
2 3
)
2
3
(
2 3
,
?
?
)
y?? ? 0 ? 0 ?
y凹
1
凸 11
27
凹
故该曲线在
(??
, 0)
及
(
2
3
,
?
?
) 上向上凹 , 在(0,
2) 上
3
向上凸
, 点(0,1)及
(2
3
,
11 27
1 (1 , 2)
0?
2 (2, ? ? ) 0?
f (x)
2
1
y
故
的单调增区间为
(??
, 1), (2, ? ? );
2
1
的单调减区间为 (1 , 2).
o 12 x
11
练习 确定 f ( x ) ? ( x ? 1) ?3 x 2 的单调区间 .

初中数学什么是函数的凹凸性如何通过函数的导函数判断其在某个区间上的凹凸性在初中数学中，函数的凹凸性描述了函数图像的弯曲程度。

一个函数可以是凹的、凸的或既不凹也不凸。

通过函数的导函数，我们可以判断函数在某个区间上的凹凸性。

在本文中，我们将详细讨论函数的凹凸性的概念以及如何通过函数的导函数判断其在某个区间上的凹凸性。

首先，让我们回顾一下函数的概念。

函数是一种对应关系，它将一个集合中的每个元素映射到另一个集合中的唯一元素。

函数通常用符号表示为f(x)，其中 f 是函数的名称，x 是自变量，f(x) 是因变量。

函数的导数可以用以下符号表示：f'(x)，其中f 是函数的名称，x 是自变量，f'(x) 是函数的导数。

函数的导数描述了函数在不同点上的变化率或斜率。

要通过函数的导函数判断其在某个区间上的凹凸性，我们可以按照以下步骤进行：步骤一：计算函数的导函数。

根据前文所述的方法，计算函数的导函数，即计算函数的导数。

步骤二：计算导函数的导数。

计算导函数的导数，即计算导函数的导数的导数，也称为二阶导数。

步骤三：判断凹凸性。

-如果二阶导数f''(x) > 0，那么函数在该区间上是凹的。

-如果二阶导数f''(x) < 0，那么函数在该区间上是凸的。

-如果二阶导数f''(x) = 0，那么函数在该区间上可能存在拐点，即既不凹也不凸。

举例来说，考虑函数f(x) = x^3。

我们将通过其导函数判断其在区间(-∞, ∞) 上的凹凸性。

步骤一：计算函数的导函数。

根据前文所述的方法，计算函数的导函数。

f'(x) = 3x^2步骤二：计算导函数的导数。

f''(x) = 6x步骤三：判断凹凸性。

对于所有的x，f''(x) = 6x > 0，所以函数f(x) 在区间(-∞, ∞) 上是凹的。

通过这个例子，我们可以看到如何通过函数的导函数判断其在某个区间上的凹凸性。

f(x)5x2 的零点2为 ，不存在的点0。 为
33 x
5
将f的符号与 f 的单调性列表如下：
x (- ,0) 0 (0,2/5) 2/5 (2/5,+ )
f + 不 存 在 - 0 +
f
连 续
连 续
f在 ( , 0上 ] 单 调[0 增 2,]上 ；单 在调[2减 ,)；
点 (0,0)是曲 y3线 x的拐 . 点
例 6、 设 yf(x)ex2,求 f(x)增 减 的 区 间 和 极 值 点 ， 以 及 凹 凸 区 间 和 拐 点 .
解：函数的定义 域 ， 为 ）（，由 y2xe x2及 y0,得 驻 x10;点
y2 e x2(2x2 1 )及 ,y0 ,得 x 2 ,32 2 1
一、渐近线
定义: 当曲y线 f(x)上的一P动 沿点 着曲线移向, 无
如果P点到某定直 L的 线距离趋向 , 于零
那么L直 就线 称为 yf曲 (x)的 线一条 . 渐近
1.铅直渐近线 (垂直于 x轴的渐近) 线
如l果 im f(x ) 或 lim f(x )
x x 0
x x 0
点x1,x2,恒有 f(x1 2x2)f(x1) 2f(x2), 那 末 称 f ( x ) 在 I 上 的 图 形 是 上 凹 的 （ 或 凹 弧 ） ;
如果 f(x 1 恒 x 2)f有 (x 1 )f(x 2),
2
2
那 末 称 f ( x ) 在 I 上 的 图 形 是 上 凸 的 （ 或 凸 弧 ） ．
解 D :(,1 ) (1 ,) .
limf(x), x1
limf(x),
x1
x 1是曲线的铅直渐.近线

x→x0 x→x0 x→x0
x 则 = x0是 数 = f ( x)的 条 直 近 . 函 y 一 垂 渐 线
y C o x y o
x0
x
曲 例1 求 线 y =
1 的 平 近 . 水 渐 线 x −1
y
2 1 -2 -1 -1 -2
y = ( x −1)
−1
1 解 Qlim =0 x→ x −1 ∞
1 一条水平渐近线 ∴ y = 0 是y = x −1
1 曲 的 垂 近 . 铅 渐 线 例2 求 线 y = x −1
O 1
2
x
1 1 解 Qlim = −∞, lim = +∞, − + x→ x −1 1 x→ x −1 1
∴x =1 y = f (x)的 条 垂 近 . 为 一 铅 渐 线
利用导数工具描绘函数的图形，称为分析法作图. 利用导数工具描绘函数的图形，称为分析法作图. 分析法作图
[ (2) f ′′( x) < 0, 则 ( x)在a,b]上的图形是凸的 f .
例1 判断函数 y = ln x的凹凸性 . 解 y 的定义域为 (0,+∞ )
1 Q y′ = x
y ′′ = − 1 x2
∴ 在(0， ∞ )内，有 y′′ < 0 +
例2 判断 y = x 3 的凹凸性 . 解
2 y ′′ = 36 x − 24 x = 36 x x − 令 y′′ = 0 3 列表
x2 =
2 3
x y" y
(−∞,0)
0 0
1(拐点)
2 , 0 3
+
－
0
11 (拐 ) 点 27

xfln (x x) y f ln ( yy ) (x x y )y x y 即 f( ln( ) ) 2 2 22 2
得证.
15
不等式证明的方法：
1、拉格朗日中定理；
2、函数的单调性、极值； 3、函数的凹凸性；
16
作业：
P 3 134
17
爱是什么？ 一个精灵坐在碧绿的枝叶间沉思。 风儿若有若无。 一只鸟儿飞过来，停在枝上，望着远处将要成熟的稻田。 精灵取出一束黄澄澄的稻谷问道：“你爱这稻谷吗？” “爱。” “为什么？” “它驱赶我的饥饿。” 鸟儿啄完稻谷，轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗？”精灵又取出一束黄澄澄的稻谷。 鸟儿抬头望着远处的一湾泉水回答：“现在我爱那一湾泉水，我有点渴了。” 精灵摘下一片树叶，里面盛了一汪泉水。 鸟儿喝完泉水，准备振翅飞去。 “请再回答我一个问题，”精灵伸出指尖，鸟儿停在上面。 “你要去做什么更重要的事吗？我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷，去看那朵风信子。” “为什么？它能驱赶你的饥饿？” “不能。” “它能滋润你的干渴？” “不能。”爱是什么？ 一个精灵坐在碧绿的枝叶间沉思。 风儿若有若无。 一只鸟儿飞过来，停在枝上，望着远处将要成熟的稻田。 精灵取出一束黄澄澄的稻谷问道：“你爱这稻谷吗？” “爱。” “为什么？” “它驱赶我的饥饿。” 鸟儿啄完稻谷，轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗？”精灵又取出一束黄澄澄的稻谷。 鸟儿抬头望着远处的一湾泉水回答：“现在我爱那一湾泉水，我有点渴了。” 精灵摘下一片树叶，里面盛了一汪泉水。 鸟儿喝完泉水，准备振翅飞去。 “请再回答我一个问题，”精灵伸出指尖，鸟儿停在上面。 “你要去做什么更重要的事吗？我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷，去看那朵风信子。” “为什么？它能驱赶你的饥饿？” “不能。” “它能滋润你的干渴？” “不能。”

2 (2,3)
3 (3,)
y
-
不存在
+
0
-
y f (x)
拐点
(2, 20 )
9
拐点
(3, 4)
结论：(,2],[3,)是曲线的凸区间,[2,3]是
曲线的凹区间； 拐点为 (2, 20), (3,4).
9
例 求曲线 y x 4 的凹凸区间和拐点
（学生练习）
例 求曲线 y earctanx的凹凸区间和拐点
y 1 x
P
x
O
点P 沿着曲线无限地远离原点时,
点P与一条定直线C 的距离趋于零, 则称直线C为曲线L的渐近线.当C 垂直于x 轴时,
称C为曲线 L的垂直渐近线；当C 垂直于y 轴时,
称C为曲线 L的水平渐近线.
y ex
ytanx
说明:
(1)直线 y y 0 是曲线 y f (x) 的水平渐近线
x0
2.曲线凹凸的判别
y=f(x)
X
观察图形中切线的斜率变化情况.
f (x) 0Y
在图1中,
Y
f (x) 0
当 x1 x2 时,
O 1 2
X
tan1tan2, 图1
2 1
X
O
图2
即 f ( x ) 是单调增加的;
在图2中,当 x1 x2 时,tan1tan2,
即 f ( x ) 是单调减少的.
三、函数的分析作图法
例 作 y 1 x 3 x 的图象 3
解(1)定义域 x(,), 并 且 图 象 关 于 原 点 对 称 .
(2) y x2 1, 得驻点 x11,x21.
y 2x, 令 y 0 得 x 0.

9
1
y 10(x2)13 10
9
9
1 0[1
(x
2)3 ]
1
9( x 2)3
x1 3 时 y 0 ; x 2 2 时 y 不存在
(3)列表
1
y 10(x2)13 10
9
9
10[1
(x
2)3 ]
1
9( x 2)3
x1 3 时 y 0; x 2 2 时 y 不存在
x
(, 2) 2 (2,3) 3 (3, )
f (x)
0
0
f(x) f (x)
0
极大值
拐点
32 27
( 1 , 16 ) 3 27
y
极小值
0
B(0,1)
C (3,5) 28
A(1,0)
1
1 o 1
1
x
3
3
yx3x2x1
四、小结
函数图形的描绘综合运用函数性态的研究,是 导数应用的综合考察.
y
凸的
单增
yf(x)
极
凹的
拐 点
大 值
0
拐点
(3, 26) 9
极小值
3
lx i m f(x)lx i [m 4(x x 21)2]2, 得水平渐近 y线 2;
lx i0m f(x)lx i0[m 4(x x 21)2] ,得 垂 直 渐 近 线 x 0 .
补充点: (13 ,0 ),(13 ,0 );
A(1,2), 作图
B(1,6), C(2,1). y
1、 曲线 y e x 的水平渐近线为_______________.
2、 曲线 y 1 的水平渐近线为______________， x1

函数凹凸性的判断方法
函数凹凸性的判断方法有以下两种：
1. 二阶求导法：对于函数f(x)，首先求出它的二阶导数f''(x)，然后根据f''(x)的符号判断函数的凹凸性。

如果f''(x)大于0，那么函数在该区间上为凸函数；如果f''(x)小于0，那么函数在该区间上为凹函数。

2. 一阶导数法：对于函数f(x)，可以通过一阶导数f'(x)的值来判断函数的凹凸性。

如果f'(x)递增，则函数在该区间上为凸函数；如果f'(x)递减，则函数在该区间上为凹函数。

需要注意的是，以上方法只适用于可导的函数，对于不可导的函数或在某些点不可导的函数，需要进行特殊处理。

另外，还需要注意函数的定义域，不同区间内的凹凸性可能会不同。

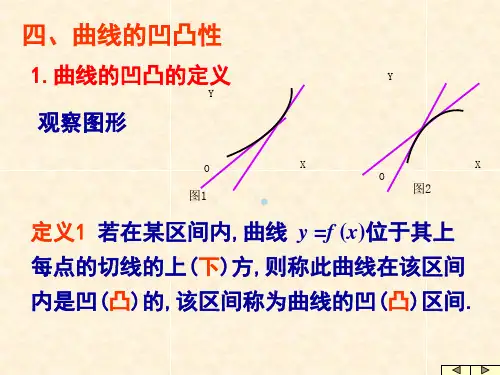
曲线凹凸性的判断方法
曲线凹凸性判断是识别函数曲线处处向量切线方向的重要方法，用于求解微积分、动力学等重要问题，也是检测函数曲线任意点处变化状态的依据。

曲线凹凸性的判断方法有以下几种：
1、利用积分法：将曲线上的每一片分段折线积分，由积分结果得出曲线的凹
凸性，即根据积分结果的符号大小来确定曲线的凹凸性：若积分结果为正，则曲线向上凸出，上升趋势明显；若积分结果为负，则曲线向下凹陷，下降趋势明显。

2、利用微分法：以曲线上任一点为中心，考察它及其附近的某点处方向与曲
线段的夹角大小及趋势，从而判断曲线凹凸性：若夹角大于零，则曲线向上凸出，上升趋势明显；若夹角小于零，则曲线向下凹陷，下降趋势明显。

3、利用数值分析法：画出曲线的网格折线，采用直接数值法求出曲线的凹凸性，即根据曲线上点之间的数值大小比较结果来判断曲线的凹凸性：若曲线点值持续上升，则曲线向上凸出，上升趋势明显；若曲线点值持续下降，则曲线向下凹陷，下降趋势明显。

4、利用图象识别法：观察曲线的图象，根据曲线的连续变化特点来确定曲线
的凹凸性，即观察曲线的拐点位置及方向确定曲线的凹凸性：若拐点持续向上，则曲线向上凸出，上升趋势明显；若拐点持续向下，则曲线向下凹陷，下降趋势明显。

以上便是曲线凹凸性判断的主要方法，各种方法有各种优缺点，在实际应用中，以上四种方法相互之间可以结合使用，以达到合理判断曲线凹凸性的效果，使曲线凹凸性判断得以正确与准确地实现。

导数与函数的凹凸性解析在数学中，函数的凹凸性是研究函数曲线的一种重要性质。

凹凸性表征了函数曲线的弯曲程度以及函数在特定区间上的增减性。

导数是研究函数变化率的工具，它与函数的凹凸性存在一定的关系。

本文将探讨导数与函数的凹凸性之间的联系，并解析凹凸性的定义以及凹凸函数的性质。

一、凹凸函数的定义一个定义在区间上的实函数，如果对于该区间上的任意两个点x1和x2，函数上的任意一点(x, f(x))都满足以下不等式：f(tx1+(1-t)x2) ≤ tf(x1) + (1-t)f(x2) (0≤t≤1)则称该函数为凹函数。

当不等式中的≤ 改为≥时，该函数则称为凸函数。

凹凸函数的定义可以通过直观理解进行解释。

对于凹函数来说，任意两个点之间的连线位于函数的图像上方或与之重合。

而对于凸函数来说，连线位于函数的图像下方或与之重合。

凹凸函数的定义可以简化为导数的定义形式，即如果函数的二阶导数大于等于零，则该函数为凹函数；若二阶导数小于等于零，则该函数为凸函数。

这是因为二阶导数表示了函数的变化率的变化率，负二阶导数说明了函数的变化率的变化率是负的，即函数的凹凸性质。

二、导数与凹凸性的关系导数是描述函数变化率的工具，它与函数的凹凸性密切相关。

具体而言，导数可以揭示函数的增长趋势，而函数的凹凸性则反映了函数增长趋势的性质。

在导数的帮助下，我们可以通过以下规则来判断函数的凹凸性：1. 如果函数的一阶导数递增，则函数是凹函数；若一阶导数递减，则函数是凸函数。

2. 如果函数的二阶导数大于零，则函数是凸函数；若二阶导数小于零，则函数是凹函数。

3. 如果函数的二阶导数恒大于零或恒小于零，则函数分别是严格凸函数和严格凹函数。

根据上述规则，我们可以利用导数信息来推断函数的凹凸性质。

导数为零的点或导数不存在的点可能是函数的拐点，即函数的凹凸性发生变化的点。

三、凹凸函数的性质凹凸函数具有一些重要的性质，这些性质在数学分析和实际应用中起着重要的作用。

例1 判断曲线 y x 3 的凹凸性.
解 y 3 x 2 , y 6 x ,
当x 0时， y 0,
曲线 在( ,0]为凸的；
当x 0时， y 0,
曲线 在[0,)为凹的；
注意到, 点(0,0)是曲线由凸变凹的分界 点.
三、曲线的拐点及其求法
x
f ( x )
f ( x)
( ,0)
0 0
拐点

凹的
( 0, 2 ) 3
凸的
2
3 0
( 2 ,) 3
凹的
( 0,1)
拐点 ( 2 , 11 ) 3 27
凹凸区间为( ,0],
[0, 2 ], 3
[ 2 ,). 3
注意: 若 f ( x0 ) 不存在, 点 ( x0 , f ( x0 )) 也可能
令 y 0 得
x1 1 , x 2 2 3 , x 3 2 3
从而三个拐点为
(1 , 1 ) ; ( 2 3 ,
1 3 1
1 3 84 3
) ; ( 2 3 ,
1
1 3 84 3
)
1 3
1 因为 8 4 3 , ( 2 3) 1 4
4.5函数曲线的凹凸性及其判别
曲线凹凸的定义
曲线的凹凸的判定
曲线的拐点及其求法
一、曲线的凹凸的定义
问题:如何研究曲线的弯曲方向?
y
y f ( x)
y
y f ( x)
o
x1
x2
x
o
x1
x2
x
图形上任意弧段 位于所张弦的下方
图形上任意弧段 位于所张弦的上方

这些实际生活中的问题，都可以用弯曲方向不同的 函数图形具体呈现出来。
二.函数的凹凸性
1.曲线凹凸性定义
问题:如何研究曲线的弯曲方向?
y y f (x)
y
y f (x)
o x1
x2 x
o x1
x2 x
二.函数的凹凸性
在区间 I 上连续,
(1）若恒有 图形是凹的；
(2）若恒有 图形是凸的；
则称 在区间 I 上的
不等式关系，得证。
四.小 结
利用二阶导数的（正负）符号可以判定函数的 凹凸性;
通过求出二阶导数等于0的点和二阶导数不存在 的点作为凹凸区间的分界点，进而确定函数的凹 凸区间;
利用函数的凹凸性证明不等式.
其中a,b均为正常数，试分析庄稼产量随氮量增长率放缓。
解： Y (N ) aN bN
D :[0, )(b
N) N N)2
ab (b N )2
0
三.典型案例
Y (N )
[
(b
ab N
)2
]
2ab (b N )3
0
在 (0, ) 内，y 0, 函数 Y (N ) 的变化率单调减少。
则称 在区间 I 上的
y
连续曲线上凹凸分界点称为拐点 x
二.函数的凹凸性
注意
1.拐点处 f (x0) 0 ，或者 f (x0 ) 不存在。 拐点两侧，二阶导数异号。
2.拐点在曲线上，因此满足曲线的方程。 3.若 (x0, f (x0 )) 是 f (x) 的拐点, 则 f (x)在 x0 处连续。
这些点将函数的定义域分成了若干的小区间。 （4）讨论二阶导数在小区间内的符号，确定凹凸性（列表） （5）考察二阶导数在以上点两侧的符号，看是否出现拐点

凹、凸的区间 .
解
2 y′′ = 36 x ( x − ). y′ = 12 x − 12 x , 3 2 令y′′ = 0, 得 x1 = 0, x2 = . 3
3 2
Q D : ( −∞ ,+∞ )
x
f ′′( x )
(−∞ ,0) −∞
+
凹的
0 0
拐点
(0, 2 ) 3 −
凸的
2
3 0
( 2 ,+∞ ) 3 +
例3
但在( −∞ ,0)内, y′′ > 0, 曲线在( −∞ ,0]上是凹的;
在(0,+∞ )内, y′′ < 0, 曲线在[0,+∞ )上是凸的.
∴ 点(0,0)是曲线 y = 3 x的拐点.
小结： 小结：
1. 可导函数单调性判别
f ′(x) > 0, x∈I f ′(x) < 0, x∈I
2.曲线的弯曲方向 曲线的弯曲方向--------凹凸性 凹凸性; 曲线的弯曲方向 凹凸性 凹凸性的判定. 凹凸性的判定
如 对 a, b) 任 两 x1 , x2 , 果 ( 内 意 点 x1 + x2 f ( x1 ) + f ( x2 ) )> , 恒 有 f( 2 2 末 f ( 那 称 ( x)在 a, b) 的 形 凸 ; 内 图 是 的
果 [ 内 续 在 如 f ( x)在 a, b] 连 ,且 (a, b)内 图 是 的 形 凹 (或 )的 那 称 ( x)在 a, b]内 图 是 (或 )的 凸 , 末 f [ 的 形 凹 凸 ;
五、曲线的拐点及其求法
1.定义 1.定义
续 线 凹 的 界 称 曲 的 点 连 曲 上 凸 分 点 为 线 拐 .

如果P点到某定直 L的 线距离趋向 , 于零
那么L直 就线 称为 yf曲 (x)的 线一条 . 渐近
1.铅直渐近线 (垂直于 x轴的渐近) 线
如l果 im f(x ) 或 lim f(x )
x x 0
x x 0
那么 xx0就是 yf(x)的一条铅直 . 渐
例如 y
1
,
(x2)(x3)
有铅直渐近线两条: x 2 , x 3 .
思考题解答
因 为f(x0)0只 是 (x0,f(x0)为 ) 拐 点
的 必 要 条 件 ，
故 ( x 0 , f ( x 0 ) 不 一 定 ) 是 拐 点 .
例 f(x)x4 x(, )f(0)0
但 (0 ,0 )并 不 是 曲 线 f(x )的 拐 点 .
第五节 函数作图
一、渐近线
定义: 当曲y线 f(x)上的一P动 沿点 着曲线移向, 无
例4 求y 曲 sx i n 线 cx o (0 ,[ s 2 ] 内 )的.拐
解 y co x s six,n y six n cx o , s
y cx o ssi x .n
令y0, 得 x134, x274.
f(3) 2 0,
4
f(7) 2 0,
4
在[0,2]内曲线有拐(点 3,为 0), (7,0).
注：利用凹凸性也可以证明一些不等式。
例2 试证 对 x ： 0、 y0， xy及 1， 有
1(xy)(xy).
2
2
解 令f(t)t , 则 f(t) ( 1 )t 2,
在 t 0 时f有 (t) 0,在t0时f是凹 。的
对 x 、 y ( 0 ),且 x y ,有
1(f(x)f(y) )f(xy),

多元二次函数凹凸性的判别方法
多元二次函数凹凸性的判别是数学中一个重要的概念，它可以帮助我们判断函数的凹凸性，从而更好地理解函数的性质。

首先，我们可以使用求导法来判断多元二次函数的凹凸性。

如果多元二次函数的导数大于0，则说明函数是凸函数；如果多元二次函数的导数小于0，则说明函数是凹函数。

其次，我们可以使用二次展开式来判断多元二次函数的凹凸性。

如果二次展开式中的常数项a大于0，则说明函数是凹函数；如果二次展开式中的常数项a小于0，则说明函数是
凸函数。

最后，我们可以使用图像法来判断多元二次函数的凹凸性。

如果函数图像的曲线向上弯曲，则说明函数是凸函数；如果函数图像的曲线向下弯曲，则说明函数是凹函数。

总之，多元二次函数凹凸性的判别有三种方法：求导法、二次展开式和图像法。

这三种方法都可以帮助我们更好地理解多元二次函数的性质，从而更好地掌握数学知识。

凹凸区间是函数的二阶导数的正负，若在某区间为正则为凹区间，若在某区间为负则为凸区间。

一般地，把满足[f(x1)+f(x2)]/2>f[(x1+x2)/2]的区间称为函数f(x)的凹区间；反之为凸区间；凹凸性改变的点叫做拐点。

通常凹凸性由二阶导数确定：满足f''(x)>0的区间为f(x)的凹区间，反之为凸区间。

曲线的凹凸分界点称为拐点，又称反曲点，在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越。

若该曲线图形的函数在拐点有二阶导数，则二阶导数在拐点处异号由正变负，由负变正或不存在。