离散系统的数字PID控制仿真

离散控制系统中的PID控制算法离散控制系统中的PID（Proportional-Integral-Derivative）控制算法是一种常用的控制算法，用于调整系统输出与设定值之间的误差，从而实现系统的稳定和精确性。

PID控制算法通过比较当前输出值和设定值，并根据比例、积分和微分三项参数的调节来计算控制器的输出，以达到最优控制效果。

一、PID控制算法的基本原理PID控制算法通过以下三个环节实现对离散控制系统的控制：1. 比例（P）环节：比例环节根据误差的大小，按比例调整控制器的输出。

它的作用是在误差较大时，加大控制器的输出，加速系统的响应速度。

比例系数越大，系统的响应越敏感，但也容易引起过冲和振荡；反之，比例系数越小，系统的响应越迟缓。

2. 积分（I）环节：积分环节根据误差的累积量，对控制器的输出进行修正。

它的作用是消除系统存在的稳态误差，使得输出逐渐接近设定值。

积分系数越大，系统对稳态误差的修正越快，但也容易引起过冲和振荡；反之，积分系数越小，系统对稳态误差的修正越慢。

3. 微分（D）环节：微分环节根据误差的变化率，对控制器的输出进行调整。

它的作用是减小系统对突变干扰的响应，提高系统的稳定性。

微分系数越大，系统对突变干扰的响应越快，但也容易引起过冲和振荡；反之，微分系数越小，系统对突变干扰的响应越慢。

二、PID控制算法的实际应用PID控制算法广泛应用于各种离散控制系统中，例如自动调节系统、温度控制系统、机器人控制系统等。

以下是PID控制算法在温度控制系统中的应用实例：1. 设置目标温度首先，需要设置目标温度作为设定值。

2. 读取当前温度值通过传感器等装置，实时读取当前温度值。

3. 计算误差将目标温度与当前温度值进行比较，得到误差值。

4. 计算PID输出根据比例、积分和微分的系数，计算出PID控制器的输出值。

5. 控制温度将PID控制器的输出值作为控制信号，通过执行机构（如加热元件）调节系统，使得温度逐渐接近目标温度。

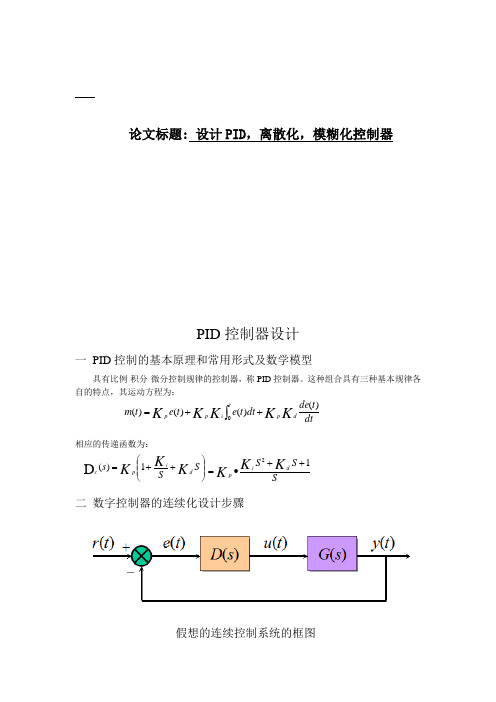
论文标题: 设计PID ，离散化，模糊化控制器PID 控制器设计一 PID 控制的基本原理和常用形式及数学模型具有比例-积分-微分控制规律的控制器，称PID 控制器。

这种组合具有三种基本规律各自的特点，其运动方程为：dt t de dt t e t e t m K K K K K dp ti p p )()()()(0++=⎰相应的传递函数为：⎪⎪⎭⎫ ⎝⎛++=S S s K K K d i p c 1)(D S S S K K K d ip 12++∙=二 数字控制器的连续化设计步骤假想的连续控制系统的框图1 设计假想的连续控制器D（s）由于人们对连续系统的设计方法比较熟悉，对由上图的假想连续控制系统进行设计，如利用连续系统的频率的特性法，根轨迹法等设计出假想的连续控制器D（S）。

2 选择采样周期T香农采样定理给出了从采样信号到恢复连续信号的最低采样频率。

在计算机控制系统中，完成信号恢复功能一般有零阶保持器H（s)来实现。

零阶保持器的传递函数为3将D（S）离散化为D（Z）将连续控制器D（S）离散化为数字控制器D（Z）的方法很多，如双线性变换法，后向差分法，前向差分法，冲击响应不变法，零极点匹配法，零阶保持法。

双线性变换法然后D（S）就可以转化离散的D（Z)三Matlab仿真实验直接试探法求PID根据这个框图，求出该传递函数的P=0.35 I=0 D=0根据⎪⎪⎭⎫ ⎝⎛++=S S s K K K d i p c 1)(D D （Z ）=0.35 T=0.01数字连续话PID 控制器设计MA TLAB 仿真框图实验结果 没有经过调节的结果为结果分析一阶阶跃信号的幅值选择为5经过数字连续化PID控制器后，对比图形发现，结果变得非常稳定，没有发现超调量，而没有经过PID控制的图形发生了超调变化达到稳定的时间变得更长。

二离散化控制器的设计离散系统设计是指在给定系统性能指标的条件下，设计出控制器的控制规律和相应的数字控制算法。

pid控制实验报告pid控制实验报告篇一：PID控制实验报告实验二数字PID控制计算机控制是一种采样控制，它只能根据采样时刻的偏差值计算控制量。

因此连续PID控制算法不能直接使用，需要采用离散化方法。

在计算机PID控制中，使用的是数字PID控制器。

一、位置式PID控制算法按模拟PID控制算法，以一系列的采样时刻点kT代表连续时间t，以矩形法数值积分近似代替积分，以一阶后向差分近似代替微分，可得离散PID位置式表达式：Tu T ?kpeu=para; J=0.0067;B=0.1; dy=zeros= y= -+ = k*ts; %time中存放着各采样时刻rineu_1=uerror_1=error;%误差信号更新图2-1 Simulink仿真程序其程序运行结果如表2所示。

Matlab输出结果errori = error_1 = 表2 例4程序运行结果三、离散系统的数字PID控制仿真1．Ex5 设被控对象为G?num 仿真程序：ex5.m%PID Controller clear all; close all;篇二：自动控制实验报告六-数字PID控制实验六数字PID控制一、实验目的1．研究PID控制器的参数对系统稳定性及过渡过程的影响。

2．研究采样周期T对系统特性的影响。

3．研究I型系统及系统的稳定误差。

二、实验仪器1．EL-AT-III型自动控制系统实验箱一台 2．计算机一台三、实验内容1．系统结构图如6-1图。

图6-1 系统结构图图中 Gc（s）=Kp（1+Ki/s+Kds） Gh（s）=（1－e）/s Gp1（s）=5/（（0.5s+1）（0.1s+1）） Gp2（s）=1/（s（0.1s+1））-TS 2．开环系统（被控制对象）的模拟电路图如图6-2和图6-3，其中图6-2对应GP1（s）,图6-3对应Gp2（s）。

图6-2 开环系统结构图1 图6-3开环系统结构图2 3．被控对象GP1（s）为“0型”系统，采用PI控制或PID控制，可使系统变为“I型”系统，被控对象Gp2（s）为“I型”系统，采用PI控制或PID控制可使系统变成“II型”系统。

实验二 数字PID 控制计算机控制是一种采样控制,它只能根据采样时刻的偏差值计算控制量;因此连续PID 控制算法不能直接使用,需要采用离散化方法;在计算机PID 控制中,使用的是数字PID 控制器;一、位置式PID 控制算法按模拟PID 控制算法,以一系列的采样时刻点kT 代表连续时间t,以矩形法数值积分近似代替积分,以一阶后向差分近似代替微分,可得离散PID 位置式表达式：式中,D p d I p i T k k T k k ==,,e 为误差信号即PID 控制器的输入,u 为控制信号即控制器的输出;在仿真过程中,可根据实际情况,对控制器的输出进行限幅;二、连续系统的数字PID 控制仿真连续系统的数字PID 控制可实现D/A 及A/D 的功能,符合数字实时控制的真实情况,计算机及DSP 的实时PID 控制都属于这种情况;1．Ex3 设被控对象为一个电机模型传递函数Bs Js s G +=21)(,式中J=,B=;输入信号为)2sin(5.0t π,采用PD 控制,其中5.0,20==d p k k ;采用ODE45方法求解连续被控对象方程;因为Bs Js s U s Y s G +==21)()()(,所以u dt dy B dty d J =+22,另y y y y ==2,1,则⎪⎩⎪⎨⎧+-==/J)*u ((B/J)y y y y 12221 ,因此连续对象微分方程函数如下 function dy = ex3ft,y,flag,parau=para;J=;B=;dy=zeros2,1;dy1 = y2;dy2 = -B/Jy2 + 1/Ju;控制主程序clear all;close all;ts=; %采样周期xk=zeros2,1;%被控对象经A/D转换器的输出信号y的初值e_1=0;%误差ek-1初值u_1=0;%控制信号uk-1初值for k=1:1:2000 %k为采样步数timek = kts; %time中存放着各采样时刻rink=sin12pikts; %计算输入信号的采样值para=u_1; % D/AtSpan=0 ts;tt,xx=ode45'ex3f',tSpan,xk,,para; %ode45解系统微分方程%xx有两列,第一列为tt时刻对应的y,第二列为tt时刻对应的y导数xk = xxend,:; % A/D,提取xx中最后一行的值,即当前y和y导数youtk=xk1; %xk1即为当前系统输出采样值ykek=rink-youtk;%计算当前误差dek=ek-e_1/ts; %计算uk中微分项输出uk=ek+dek;%计算当前uk的输出%控制信号限幅if uk>uk=;endif uk<uk=;end%更新uk-1和ek-1u_1=uk;e_1=ek;endfigure1;plottime,rin,'r',time,yout,'b';%输入输出信号图xlabel'times',ylabel'rin,yout';figure2;plottime,rin-yout,'r';xlabel'times',ylabel'error';%误差图程序运行结果显示表1所示;表1 程序运行结果分析:输出跟随输入,PD 控制中,微分控制可以改善动态特性,调节时间缩短,允许加大比例控制,使稳态误差减小,提高了控制精度.2．Ex4 被控对象是一个三阶传递函数ss s 1047035.8752350023++,采用Simulink 与m 文件相结合的形式,利用ODE45方法求解连续对象方程,主程序由Simulink 模块实现,控制器由m 文件实现;输入信号为一个采样周期1ms 的正弦信号;采用PID 方法设计控制器,其中05.0,2,5.1===d i p k k k ;误差初始化由时钟功能实现,从而在m 文件中实现了误差的积分和微分;控制主程序：控制子程序：function u=ex4fu1,u2%u1为Clock,u2为图2-1中Sum 模块输出的误差信号e 的采样值 persistent errori error_1if u1==0 %当Clock=0时,即初始时,ek=ek-1=0errori=0error_1=0endts=;kp=;ki=;kd=;error=u2;errord=error-error_1/ts;%一阶后向差分误差信号表示的误差微分errori=errori+errorts;%累积矩形求和计算的误差的积分u=kperror+kderrord+kierrori;%由PID 算式得出的当前控制信号ukerror_1=error;%误差信号更新图2-1 Simulink 仿真程序其程序运行结果如表2所示;Matlab 输出结果errori =error_1 =表2 例4程序运行结果三、离散系统的数字PID 控制仿真1．Ex5 设被控对象为ss s s G 1047035.87523500)(23++=,采样时间为1ms,对其进行离散化;针对离散系统的阶跃信号、正弦信号和方波信号的位置响应,设计离散PID 控制器;其中S 为信号选择变量,S=1时是阶跃跟踪,S=2时为方波跟踪,S=3时为正弦跟踪;求出Gs 对应的离散形式)()()(z U z Y z G =,其中Yz 和Uz 是关于z 的多项式,则可以得到其对应的差分表达式仿真程序：%PID Controllerclear all;close all;ts=;%采样周期sys=tf,1,,,0;%被控对象连续传递函数dsys=c2dsys,ts,'z';%转换成离散z 传递函数的形式num,den=tfdatadsys,'v';%提取z 传递函数中的分子和分母多项式系数u_1=;u_2=;u_3=;%uk-1、uk-2、uk-3的初值y_1=;y_2=;y_3=; %yk-1、yk-2、yk-3的初值x=0,0,0'; %比例、微分、积分项的初值error_1=0;%ek-1的初值disp'S=1--step,S=2--sin,S=3--square'% S=1阶跃,S=2方波,S=3正弦S=input'Number of input signal S:'%接收输入信号代号for k=1:1:1500timek=kts;%各采样时刻if S==1 %阶跃输入时kp=;ki=;kd=; %各项PID系数rink=1; %阶跃信号输入elseif S==2kp=;ki=;kd=; %各项PID系数rink=signsin22pikts; %方波信号输入elseif S==3kp=;ki=;kd=; %各项PID系数rink=sin22pikts; %正弦信号输入enduk=kpx1+kdx2+kix3; %PID控制信号输出uk%控制信号输出限幅if uk>=10uk=10;endif uk<=-10uk=-10;end%根据差分方程计算系统当前输出ykyoutk=-den2y_1-den3y_2-den4y_3+num2u_1+num3u_2+num4u_3; errork=rink-youtk;%当前误差%更新uk-1、uk-2、uk-3、yk-1、yk-2、yk-3u_3=u_2;u_2=u_1;u_1=uk;y_3=y_2;y_2=y_1;y_1=youtk;x1=errork; %比例输出x2=errork-error_1/ts; %微分输出x3=x3+errorkts; %积分输出error_1=errork; %更新ek-1endfigure1; %作图plottime,rin,'r',time,yout,'b';xlabel'times',ylabel'rin,yout';其程序运行结果如表3所示;2．Ex6针对于Ex5被控对象所对应的离散系统,设计针对三角波、锯齿波和随机信号的位置式响应;仿真程序：;程序中当S=1时为三角波,S=2时为锯齿波,S=3时为随机信号;如果D=1,则通过pause命令实现动态演示仿真;%PID Controllerclear all;close all;ts=;sys=tf,1,,,0;dsys=c2dsys,ts,'z';num,den=tfdatadsys,'v';u_1=;u_2=;u_3=;r_1=rand;y_1=0;y_2=0;y_3=0;x=0,0,0';error_1=0;disp'S=1--Triangle,S=2--Sawtooth,S=3--Random'% S=1三角,S=2锯齿,S=3随机S=input'Number of input signal S:'%接收输入信号代号disp'D=1--Dynamic display,D~=1--Direct display'%D=1动画显示,D~=1直接显示D=input'D='for k=1:1:3000timek=kts;kp=;ki=;kd=;if S==1 %Triangle Signalif modtimek,2<1rink=modtimek,1;elserink=1-modtimek,1;endrink=rink;endif S==2 %Sawtooth Signalrink=modtimek,;endif S==3 %Random Signalrink=rand;vrk=rink-r_1/ts; %Max speed iswhile absvrk>=rink=rand;vrk=absrink-r_1/ts;endenduk=kpx1+kdx2+kix3; %PID Controller%Restricting the output of controllerif uk>=10uk=10;endif uk<=-10uk=-10;end%Linear modelyoutk=-den2y_1-den3y_2-den4y_3+num2u_1+num3u_2+num4u_3; errork=rink-youtk;r_1=rink;u_3=u_2;u_2=u_1;u_1=uk;y_3=y_2;y_2=y_1;y_1=youtk;x1=errork; %Calculating Px2=errork-error_1/ts; %Calculating Dx3=x3+errorkts; %Calculating Ixik=x3;error_1=errork;if D==1 %Dynamic Simulation Displayplottime,rin,'b',time,yout,'r';pause;endendplottime,rin,'r',time,yout,'b';xlabel'times';ylabel'rin,yout';Matlab运行结果为：S=1--Triangle,S=2--Sawtooth,S=3--RandomNumber of input signal S:12、3S =1D=1--Dynamic display,D=0--Direct display %D=1动画显示,D~=1直接显示D=0D =0 %D=0直接显示,如果D=1,则通过pause命令实现动态演示仿真;其程序运行结果如表4所示;表4 程序运行结果分析：s=1时为三角波的位置式响应,s=2时为锯齿波的位置式响应；s=3时为随机信号的位置式响应;3．Ex7 采用Simulink实现PID控制器的设计,如图2-2所示,其中离散PID控制的子系统如图2-3所示,其封装界面如图2-4所示;仿真程序：图2-2 离散PID控制的Simulink主程序图2-3 离散PID控制的Simulink控制器程序图2-4 离散PID控制的封装界面其程序运行结果如表5所示;分析：位置式PID控制算法的缺点是,由于采用全量输出,所以每次输出均与过去的状态有关,计算时要对ek量进行累加,计算机输出控制量uk对应的是执行机构的实际位置偏差,如果位置传感器出现故障,uk 可能会出现大幅度变化;uk 大幅度变化会引起执行机构未知的大幅度变化,这种情况在生产中是不允许的,在某些重要场合还可能造成重大事故;为了避免这种情况的发生,可采用增量式PID 控制算法;四、增量式PID 控制算法及仿真当执行机构需要的是控制量的增量例如驱动步进电机时,应采用增量式PID 控制,根据递推原理可得增量式PID 控制算法为Ex8 设被控对象ss s G 50400)(2+=,采用增量式控制算法,PID 控制参数10,1.0,8===d i p k k k ; 仿真程序：%Increment PID Controllerclear all;close all;ts=;sys=tf400,1,50,0;dsys=c2dsys,ts,'z';num,den=tfdatadsys,'v';u_1=;u_2=;u_3=;y_1=0;y_2=0;y_3=0;x=0,0,0';error_1=0;error_2=0;for k=1:1:1000timek=kts;rink=;kp=8;ki=;kd=10;duk=kpx1+kdx2+kix3;uk=u_1+duk;if uk>=10 uk=10; end if uk<=-10 uk=-10; endyoutk=-den2y_1-den3y_2+num2u_1+num3u_2; error=rink-youtk;u_3=u_2;u_2=u_1;u_1=uk; y_3=y_2;y_2=y_1;y_1=youtk;x1=error-error_1; %Calculating P x2=error-2error_1+error_2; %Calculating D x3=error; %Calculating I error_2=error_1; error_1=error; endplottime,rin,'b',time,yout,'r'; xlabel'times';ylabel'rin,yout'; 其程序运行结果如图5所示;分析：增量式PID 控制算法计算的误差小;由于他只输出控制量,所以误动作时影响小,系统的超调及振动也少;由于控制算法中不需要累加,控制增量Δuk 仅与最近k 次的采样有关,所以误动作影响小,而且较容易通过加权处理获得比较好的控制效果;仿真程序运行结果：PID 控制参数10,1.0,8===d i p k k k ;图5 增量式PID 控制算法仿真结果实验三 PID 控制的改进算法在计算机控制系统中,PID 控制是通过计算机程序实现的,因此灵活性很大;一些原来在模拟PID 控制器中无法实现的问题,在引入计算机以后,就可以得到解决,于是产生了一系列的改进算法,形成非标准的控制算法,以改善系统品质,满足不同控制系统的需要;一、积分分离PID 控制算法在普通PID 控制中,积分的目的是为了消除金叉,提高精度,但在过程的启动、结束或大幅度增减设定是,短时间内系统输出有很大偏差,会造成PID 运算的积分积累,致使控制量超过执行机构可能允许的最大动作范围对应的极限控制量,引起系统较大的超调,甚至引起系统较大的振荡,这在生产中是绝对不允许的;积分分离控制基本思路是,当被控量与设定值偏差较大时,取消积分作用,以免由于积分作用使系统稳定性降低,超调量增大；当被控量接近给定值时,引入积分控制,以便消除静差,提高控制精度;其具体实现步骤是：1）根据实际情况,人为设定阈值ε>0；2）当ε>)(k e 时,采用PD 控制,可避免产生过大的超调,又使系统有较快的响应； 3）当ε≤)(k e 时,采用PID 控制,以保证系统的控制精度; 积分分离算法可表示为：式中,T 为采样时间,β为积分项的开关系数,⎩⎨⎧>≤=ξξβ|)(|0|)(|1k e k eEx9 设备控对象为一个延迟对象160)(80+=-s e s G s,采样周期为20s,延迟时间为4个采样周期,即80s;输入信号rk=40,控制器输出限制在-110,110;3,005.0,8.0===d i p k k k 被控对象离散化为)5()2()1()2()(-+--=k u num k y den k y仿真方法一：仿真程序：;当M=1时采用分段积分分离法,M=2时采用普通PID 控制; %Integration Separation PID Controller clear all; close all; ts=20; %Delay plantsys=tf1,60,1,'inputdelay',80; dsys=c2dsys,ts,'zoh'; num,den=tfdatadsys,'v';u_1=0;u_2=0;u_3=0;u_4=0;u_5=0; y_1=0;y_2=0;y_3=0;error_1=0;error_2=0;ei=0;% M=1分段积分分离,M=2普通PIDdisp'M=1--Using integration separation,M=2--Not using integration separation' M=input'whether or not use integration separation method:'for k=1:1:200timek=kts;%输出信号youtk=-den2y_1+num2u_5;rink=40;errork=rink-youtk;ei=ei+errorkts;%积分项输出if M==1 %使用分段积分分离if abserrork>=30&abserrork<=40beta=;elseif abserrork>=20&abserrork<=30beta=;elseif abserrork>=10&abserrork<=20beta=;elsebeta=;endelseif M==2beta=;endkp=;ki=;kd=;uk=kperrork+kderrork-error_1/ts+betakiei;if uk>=110 % 控制信号限幅uk=110; end if uk<=-110 uk=-110; endu_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=uk; y_3=y_2;y_2=y_1;y_1=youtk; error_2=error_1; error_1=errork; end figure1;plottime,rin,'b',time,yout,'r'; xlabel'times';ylabel'rin,yout'; figure2; plottime,u,'r'; xlabel'times';ylabel'u'; 其程序运行结果表1所示;表1 例9仿真方法一结果分析：积分饱和的防止方法有积分分离法和预限削弱法;积分作用使系统稳定性降低,超调量增大;比较仿真结果,当被控量与设定值偏差较大时,删除积分作用,以使∑=kj j e 0)(不至过大;只有当)(k e 较小时方引入积分作用,以消除静差,提高控制精度,控制量不宜进入饱和区;仿真方法二：采用Simulink 仿真初始化程序clear all;close all;ts=20;sys=tf1,60,1,'inputdelay',80;dsys=c2dsys,ts,'zoh';num,den=tfdatadsys,'v';kp=;ki=;kd=;Simulink主程序,如图3-1所示;图3-1 Simulink主程序其运行结果如表2所示;表2 Simulink仿真结果分析：由图可知,积分时间常数能消除系统的稳态误差,提高系统控制精度,只有当积分时间常数合适时,过度过程的特性才比较理想;积分时间常数过小,系统震荡次数多,积分时间常数过大,对系统性能影响减少;二、抗积分饱和PID控制算法所谓积分饱和是指若系统存在一个方向的偏差,PID控制器的输出由于积分作用的不断累加而加大,从而导致执行机构达到极限位置Xmax,若控制器输出uk继续增大,阀门开度不可能在增大,此时就称计算机输出控制超出正常运行范围而进入了饱和区;一旦系统出现反向偏差,uk逐渐从饱和区推出;进入饱和区越深,则退出饱和区所需时间越长;在这段时间内,执行机构仍停留在极限位置而不能随偏差反向立即作出相应的改变,这时系统就像失去控制一样,造成控制性能恶化;这种现象称为积分饱和现象或积分失控现象;抗积分饱和的思路是,在计算uk时,首先判断上一时刻的控制量uk-1是否已超出限制范围;若uk-1>u max ,则只累加负偏差；若uk-1<u min ,则只累加正偏差;这种算法可以避免控制量长时间停留在饱和区;Ex10 设被控对象为ss s s G 1047035.87523500)(23++=,采样周期1ms;输入rk=30,0,9,85.0===d i p k k k仿真程序：;M=1时采用抗积分饱和算法,M=2时采用普通PID 算法; %PID Controler with intergration sturation clear all; close all; ts=; sys=tf,1,,,0; dsys=c2dsys,ts,'z'; num,den=tfdatadsys,'v'; u_1=;u_2=;u_3=; y_1=0;y_2=0;y_3=0; x=0,0,0'; error_1=0;um=6;%控制信号限幅值 kp=;ki=;kd=;rin=30; %Step Signal % M=1抗积分饱和,M=2普通PIDdisp'M=1--Using intergration sturation,M=2--Not using iintergration sturation' M=input'whether or not use integration separation method:' for k=1:1:800 timek=kts;uk=kpx1+kdx2+kix3; % PID Controller if uk>=um uk=um; end if uk<=-umuk=-um;end%Linear modelyoutk=-den2y_1-den3y_2-den4y_3+num2u_1+num3u_2+num4u_3; errork=rin-youtk;if M==1 %Using intergration sturationif uk>=umif errork>0alpha=0;elsealpha=1;endelseif uk<=-umif errork>0alpha=1;elsealpha=0;endelsealpha=1;endelseif M==2 %Not using intergration sturationalpha=1;end%Return of PID parametersu_3=u_2;u_2=u_1;u_1=uk;y_3=y_2;y_2=y_1;y_1=youtk;error_1=errork;x1=errork; % 计算比例项x2=errork-error_1/ts; % 计算微分项x3=x3+alphaerrorkts; % 计算积分项 xik=x3; end figure1; subplot311;plottime,rin,'b',time,yout,'r';xlabel'times';ylabel'Position tracking'; subplot312; plottime,u,'r';xlabel'times';ylabel'Controller output'; subplot313; plottime,xi,'r';xlabel'times';ylabel'Integration'; 其运行结果如表3所示;表3 例10仿真结果分析:比较仿真结果知,采用普通的算法时,积分项的存在,有时可能会引起积分饱和,增加系统的调整时间和超调量,而采用了抗积分饱和的方法,可以消除静态误差,使控制量不易进入饱和区,即使进入了,也能较快,系统的输出特性得到了一定改善;三、不完全微分PID 控制算法在PID 控制中,微分信号的引入可改善系统的动态特性,但也易引入高频干扰,在误差扰动突变时尤其显出微分项的不足;若在控制算法中加入低通滤波器,则可使系统性能得到改善;具体做法就是在PID 算法中加入一个一阶惯性环节低通滤波器sT f +11,T f 为滤波器系数;可得此时的微分项输出为()())1()1()()1()1()()1()(-+---=--++-+=k u k e k e K k e k e T T T k k u T T T k u D D f s DpD fs f D αα,其中)1(-+=k u T T T D fs f α,sDpD T T k K =,T s 为采样时间,T D 为微分时间常数; Ex11 被控对象为时滞系统传递函数160)(80+=-s e s G s,在对象的输出端加幅值为的随机信号;采样周期为20ms;采用不完全微分算法,140,0055.0,3.0===D i p T k k ;所加的低通滤波器为11801)(+=s s Q仿真程序：;M=1时采用不完全微分,M=2时采用普通PID %PID Controler with Partial differential clear all; close all; ts=20;sys=tf1,60,1,'inputdelay',80; dsys=c2dsys,ts,'zoh'; num,den=tfdatadsys,'v';u_1=0;u_2=0;u_3=0;u_4=0;u_5=0; %控制信号初值 ud_1=0; %uDk-1初值y_1=0;y_2=0;y_3=0; %输出信号初值 error_1=0; ei=0; for k=1:1:100 timek=kts; rink=;youtk=-den2y_1+num2u_5; %输出信号差分方程 Dk=rands1;%干扰信号youtk=youtk+Dk; %加入干扰后的输出信号 errork=rink-youtk;ei=ei+errorkts; %矩形面积求和计算的积分项输出 kp=; ki=;TD=140;kd=kpTD/ts;Tf=180;%Q的滤波器系数Q=tf1,Tf,1; %低通滤波器%M=1选择不完全微分,M=2选择普通PIDdisp'M=1—Using Partial differential PID,M=2-- Using PID Controler without Partial differential'M=input'whether or not use Partial differential PID:'if M==1 %M=1时用不完全微分alfa=Tf/ts+Tf;udk=kd1-alfaerrork-error_1+alfaud_1;uk=kperrork+udk+kiei;ud_1=udk;elseif M==2 %M=2时用普通PIDuk=kperrork+kderrork-error_1+kiei;end%输出限幅if uk>=10uk=10;endif uk<=-10uk=-10;end%更新采样值u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=uk;y_3=y_2;y_2=y_1;y_1=youtk;error_1=errork;endfigure1;plottime,rin,'b',time,yout,'r';xlabel'times';ylabel'rin,yout'; figure2; plottime,u,'r'; xlabel'times';ylabel'u'; figure3;plottime,rin-yout,'r'; xlabel'times';ylabel'error'; figure4; bodeQ,'r'; dcgainQ;其运行结果如表4所示;分析：比较m=1与m=2的图可得知：在标准PID 算式中,当有阶跃信号输入时,微分想输出急剧增加,容易引起调节过程的震荡,导致品质因数下降,为了克服这点才引入不完全微分的PID 算法;其微分作用逐渐下降,微分输出信号按指数规律逐渐衰减到零,因而系统变化比较缓慢,不容易引起振荡;微分控制可以改善动态特性,如超调量减少,调节时间缩短,使稳态误差减少,提高控制精度;表4 例11运行结果四、微分线性PID 控制算法微分线性的PID 控制结构如图3-2所示,其特点是只对输出量yk 进行微分,而对给定值rk 不进行微分;这样,在改变给定值时,输出不会改变,而被控量的变化通常是比较缓和的,它适用于给定值rk 频繁升降的场合,可以避免给定值升降时引起的系统振荡,从而改善系统的动态特性;图3-2 微分先行PID 控制结构图 令微分部分的传递函数为111)()(<++=γγs T s T s y s u D D D ,式中11+s T D γ相当于低通滤波器;则有y dtdyT u dt du T D D D D+=+γ 由差分得：)()1()()()1()(k y Tk y k y T k u T k u k u T D D D D D+--=+--γ整理得微分部分的输出：)1()()1()(321--+-=k y c k y c k u c k u D D 其中TT T c T T T T c TT T c D DD D D D +=++=+=γγγγ321,,比例积分部分的传递函数为：⎪⎪⎭⎫⎝⎛+=s T k s E s u I p PI 11)()(,其中T I 为积分时间常数; 离散控制算式为)()()(k u k u k u D PI +=;Ex12 设被控对象为一个延迟对象160)(80+=-s e s G s,采样周期为20s;输入信号为带有高频干扰的方波信号：))03.0sin(05.0)0005.0sgn(sin()(t t t r ππ+=;普通PID 控制中 14,0021.0,36.0===d i p k k k ;微分先行PID 中γ=;仿真程序：;M=1时使用微分先行PID,M=2使用普通PID %PID Controler with differential in advance clear all; close all; ts=20;sys=tf1,60,1,'inputdelay',80; dsys=c2dsys,ts,'zoh'; num,den=tfdatadsys,'v';u_1=0;u_2=0;u_3=0;u_4=0;u_5=0; ud_1=0;y_1=0;y_2=0;y_3=0; error_1=0;error_2=0; ei=0;%M=1使用微分先行PID,M=2使用普通PIDdisp'M=1aUsing PID Controler with differential in advance ,M=2-- Using common PID Controler'M=input'whether or not use PID Controler with differential in advance:';for k=1:1:400timek=kts;%Linear modelyoutk=-den2y_1+num2u_5;kp=;kd=14;ki=;rink=signsin2pikts;rink=rink+sinpikts;errork=rink-youtk;ei=ei+errorkts;gama=;Td=kd/kp;c1=gamaTd/gamaTd+ts;c2=Td+ts/gamaTd+ts;c3=Td/gamaTd+ts;if M==1 %PID Control with differential in advanceudk=c1ud_1+c2youtk-c3y_1;uk=kperrork+udk+kiei;elseif M==2 %Simple PID Controluk=kperrork+kderrork-error_1/ts+kiei;endif uk>=110uk=110;endif uk<=-110uk=-110;end%Update parametersu_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=uk; y_3=y_2;y_2=y_1;y_1=youtk; error_2=error_1; error_1=errork; end figure1;plottime,rin,'r',time,yout,'b'; xlabel'times';ylabel'rin,yout'; figure2; plottime,u,'r'; xlabel'times';ylabel'u'; 其运行结果如表5所示;分析：微分先行PID 算法将微分算法放在前面,适用于给定量频繁升降的场合,可以避免给定值升降时引起的系统振荡,从而改善系统的动态特性;表5 例12仿真结果五、带死区的PID 控制算法某些系统为了避免控制作用过于频繁,消除由于频繁动作所引起的振荡,可采用带死区的PID 控制算法,控制算法为：⎩⎨⎧>≤=Bk e k e Bk e k e )()()(0)(,式中ek 为位置跟踪偏差,B 为可调的死区参数,具体可根据实际控制对象由试验确定;若B 太小,会使控制动作过于频繁,达不到稳定被控对象的目的；若B 太大,则系统将产生较大的滞后;Ex13 设被控对象为ss s s G 1047035.87523500)(23++=,采样周期为1ms,对象输出上有一个幅值为的正态分布的随机干扰信号;采用积分分离式PID 控制算法进行阶跃响应,取ξ=,死区参数B=,采用低通滤波器对对象输出信号进行滤波,滤波器为104.01)(+=s s Q ;仿真程序：;M=1时,采用一般积分分离式PID 控制算法,M=2时采用带死区的积分分离式PID控制算法;%PID Controler with dead zoneclear all;close all;ts=;sys=tf,1,,,0;dsys=c2dsys,ts,'z';num,den=tfdatadsys,'v'u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;y_1=0;y_2=0;y_3=0;yy_1=0;error_1=0;error_2=0;ei=0;sys1=tf1,,1; %Low Freq Signal Filterdsys1=c2dsys1,ts,'tucsin';num1,den1=tfdatadsys1,'v';f_1=0;%M=1选择普通积分分离式PID,M=2选择带死区的积分分离式PID算法disp'M=1--Using common integration seperation PID Controler ,M=2-- Using integration seperation PID Controler with dead zone'M=input'whether or not use integration seperation PID Controler with dead zone:';for k=1:1:2000timek=kts;rink=1; %Step Signal%Linear modelyoutk=-den2y_1-den3y_2-den4y_3+num2u_1+...num3u_2+num4u_3Dk=rands1; %Disturbance signalyyoutk=youtk+Dk;%Low frequency filterfiltyk=-den12f_1+num11yyoutk+yy_1;errork=rink-filtyk;if abserrork<=ei=ei+errorkts;elseei=0;endkp=;ki=;kd=;uk=kperrork+kiei+kderrork-error_1/ts;if M==1uk=uk;elseif M==2 %Using Dead zoneif abserrork<=uk=0;endendif uk>=10uk=10;endif uk<=-10uk=-10;end%----------Return of PID parameters------------ rin_1=rink;u_3=u_2;u_2=u_1;u_1=uk;y_3=y_2;y_2=y_1;y_1=youtk;f_1=filtyk;yy_1=yyoutk;error_2=error_1;error_1=errork;endfigure1;subplot211;plottime,rin,'r',time,filty,'b';xlabel'times';ylabel'rin,yout';subplot212;plottime,u,'r';xlabel'times';ylabel'u';figure2;plottime,D,'r';xlabel'times';ylabel'Disturbance signal';其运行结果如表6所示;表6 例13仿真结果分析：在控制精度要求不太高,控制过程要求尽量平稳的场合,为了避免控制动作过于频繁,消除由此产生的震荡,可以认为设置一灵敏区;死区是一可调参数,参数太小,调节动作过于频繁,达不到稳定控制的目的,参数太大,又会产生很大的纯滞后;实验四纯滞后系统的控制算法一、纯滞后系统的Smith控制算法在工业过程控制中,许多被控对象具有纯滞后的性质;Smith提出了一中纯滞后补偿模型,其原理为,与PID控制器并接一个补偿环节,该补偿环节称为Smith预估器;被控对象传递函数为spesGτ-)(,模拟调节器的传递函数为)(sD,则系统的闭环传递函数为spspesGsDesGsDsττ--+=Φ)()(1)()()(;可见,闭环特征方程中出现了纯滞后环节,使系统稳定性降低,如果滞后时间τ足够大,系统将不稳定,这就是大延迟过程难于控制的本质;针对这一问题,Smith提出在调节器上反向并联一个预估模型,Smith预估控制系统等效图如图4-1所示;图4-1带Smith预估器的控制系统Ex14 设被控对象为160)(80+=-s e s G sp ,采用Smith 控制方法,在PI 控制中,取022.0,4==i p k k ,输入阶跃信号幅值为100;仿真程序：其运行结果如表1所示;分析：纯滞后性质常引起系统产生超调或者振荡,使系统的稳定性降低;s e τ-项在闭环控制回路之外,不影响系统的稳定性,仅将控制作用在时间坐标轴上推迟了一个时间τ,控制系统的过渡过程及其他性能指标都与对象特征为)(s G p 的完全相同,消除了纯滞后部分对控制系统的影响;表1 例14运行结果二、大林控制算法早在1968年,美国IBM 公司的大林就提出了一种不同常规PID 控制规律的新型算法, 即大林控制算法,该算法的最大特点是,将期望的闭环响应设计成一阶惯性加延迟,然后反过来得到能满足这种闭环响应的控制器;对于单回路控制系统,Dz 为数字控制器,Gz 为被控对象广义传递函数,则闭环系统传递函数为：)()(1)()()()()(z G z D z G z D z R z C z +==Φ则有)(1)()(1)()()(z z z G z E z U z D Φ-Φ==;如果能事先设定系统的闭环响应)(z Φ,则可得到控制器Dz;大林之处,通常的期望闭环响应是一阶惯性加纯延迟形式,其延迟时间等于对象的纯延迟时间τ：1)()()(+==Φ-s T e s R s C s sττ式中,τT 为闭环系统的时间常数,由此得到的控制率称为大林控制算法;Ex15 设被控对象为14.0)(76.0+=-s e s G sp ,采样时间为;期望的闭环响应设计为：115.0)()()(76.0+==Φ-s e s R s C s s仿真程序：;M=1时为采用大林控制算法,M=2时为采用普通PID算法;%Delay Control with Dalin Algorithmclear all;close all;ts=;%Plantsys1=tf1,,1,'inputdelay',;dsys1=c2dsys1,ts,'zoh';num1,den1=tfdatadsys1,'v';%Ideal closed loopsys2=tf1,,1,'inputdelay',;dsys2=c2dsys2,ts,'zoh';%Design Dalin controllerdsys=dsys2/dsys11-dsys2;num,den=tfdatadsys,'v';u_1=;u_2=;u_3=;u_4=;u_5=;y_1=;error_1=;error_2=;error_3=;ei=0;%选择是否使用大林算法,M=1使用,M=2不使用disp'M=1aUsing Dalin Method ,M=2-- Using common PID Controler' M=input'whether or not use Dalin Method:';for k=1:1:50timek=kts;rink=; %Tracing Step Signalyoutk=-den12y_1+num12u_2+num13u_3;errork=rink-youtk;if M==1 %Using Dalin Methoduk=num1errork+num2error_1+num3error_2+num4error_3-den3u_1-den4u_2-den5u_3-den6u_4-den7u_5/den2;elseif M==2 %Using PID Methodei=ei+errorkts;uk=errork+errork-error_1/ts+ei;end%----------Return of dalin parameters------------u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=uk;y_1=youtk;error_3=error_2;error_2=error_1;error_1=errork;endplottime,rin,'b',time,yout,'r';xlabel'times';ylabel'rin,yout';其程序运行结果如表2所示;分析：大林控制算法,该算法的最大特点是,将期望的闭环响应设计成一阶惯性加延迟,然后反过来得到能满足这种闭环响应的控制器;大林算法很好的抑制了振铃现象;用大林算法设计的数字控制器系统输出超调量小甚至没有,并且允许有交长时间的调整时间;表2 大林算法与普通PID算法比较。

PID控制算法的简单分析和仿真！PID算法简单剖析如下：1、⾸先我们来看⼀下PID系统的基本组成模块：如图所⽰，图中相关参数的表⽰如下：r(t)：系统实际上需要的输出值，这是⼀个标准值，在我们设定了之后让这个系统去逼近的⼀个值（随时间变化的原因是，我们对系统的需求不同才会改变！）y(t)：系统当前的输出值，这个值应该需要趋近于我们设定的值，当我们没有增加PID控制模块之前，它是由被控对象通过r(t)输⼊直接产⽣的。

e(t)：系统由于某些扰动，导致的系统产⽣的偏差，实际输出的值和想要设定的初始值r(t)的差值。

u(t)：系统通过PID控制器输出的新的输⼊值，实际上他是在r(t)的基础上，针对当前的实际情况做出的改变。

Kp⽐例模块：系统PID⽐例因⼦，Kp能够对于产⽣的偏差e(t)能够迅速的作出反应，减少偏差。

Ki积分模块：系统PID积分因⼦，Ki能够⽤于消除静差，由于前⾯的误差有正有负，所以当前偏差的加⼊能够抵消部分，保持系统的稳定性，让系统有记忆功能。

Kd微分模块：系统微分因⼦，Kd能够体现出当前误差的变化趋势，引⼊有效早期修正信号，从⽽加快系统的动作速度，减少调节时间。

图中所⽰的信号关系公式如下所⽰：信号误差公式：模拟信号的PID控制器公式：离散信号的PID控制器公式：被控对象的信号公式：（简单的线性系统，⽐如电机的PWM调速系统）上述公式参数描述：Kp控制器⽐例系数、Ti控制器积分时间(积分系数）、Td控制器微分时间(微分系数）k采样序列号，k=0,1,2,3...、Uk第k次采样时刻系统输出值、ek第k次采样时刻偏差值、ek-1第k-1次采样时刻偏差值、Ki=Kp*T/Ti、Kd=Kp*Td/T2、离散信号的PID控制器算法仿真：1、位置式PID算法：PID系统产⽣的值，完全作为系统的输⼊参数，即采⽤u(k)代替了r(k)，如果计算机出现故障时，位置式PID控制将导致Uk的剧烈变化，这会引起执⾏机构的⼤幅度变化，造成巨⼤损失。

实验二 数字PID 控制计算机控制是一种采样控制，它只能根据采样时刻的偏差值计算控制量。

因此连续PID 控制算法不能直接使用，需要采用离散化方法。

在计算机PID 控制中，使用的是数字PID 控制器。

一、位置式PID 控制算法按模拟PID 控制算法，以一系列的采样时刻点kT 代表连续时间t ，以矩形法数值积分近似代替积分，以一阶后向差分近似代替微分，可得离散PID 位置式表达式：∑∑==--++=⎪⎪⎭⎫ ⎝⎛--++=k j di p k j D I p T k e k e k T j e k k e k k e k e T T j e T T k e k k u 00)1()()()())1()(()()()( 式中，D p d I pi T k k T k k ==,，e 为误差信号（即PID 控制器的输入），u 为控制信号（即控制器的输出）。

在仿真过程中，可根据实际情况，对控制器的输出进行限幅。

二、连续系统的数字PID 控制仿真连续系统的数字PID 控制可实现D/A 及A/D 的功能，符合数字实时控制的真实情况，计算机及DSP 的实时PID 控制都属于这种情况。

1．Ex3 设被控对象为一个电机模型传递函数BsJs s G +=21)(，式中J=0.0067,B=0.1。

输入信号为)2sin(5.0t π，采用PD 控制，其中5.0,20==d p k k 。

采用ODE45方法求解连续被控对象方程。

因为Bs Js s U s Y s G +==21)()()(，所以u dt dy B dty d J =+22，另y y y y ==2,1，则⎪⎩⎪⎨⎧+-==/J)*u ((B/J)y y y y 12221 ，因此连续对象微分方程函数ex3f.m 如下 function dy = ex3f(t,y,flag,para)u=para;J=0.0067;B=0.1;dy=zeros(2,1);dy(1) = y(2);dy(2) = -(B/J)*y(2) + (1/J)*u;控制主程序ex3.mclear all;close all;ts=0.001; %采样周期xk=zeros(2,1);%被控对象经A/D转换器的输出信号y的初值e_1=0;%误差e(k-1)初值u_1=0;%控制信号u(k-1)初值for k=1:1:2000 %k为采样步数time(k) = k*ts; %time中存放着各采样时刻rin(k)=0.50*sin(1*2*pi*k*ts); %计算输入信号的采样值para=u_1; % D/AtSpan=[0 ts];[tt,xx]=ode45('ex3f',tSpan,xk,[],para); %ode45解系统微分方程%xx有两列，第一列为tt时刻对应的y，第二列为tt时刻对应的y导数xk = xx(end,:); % A/D，提取xx中最后一行的值，即当前y和y导数yout(k)=xk(1); %xk(1)即为当前系统输出采样值y(k)e(k)=rin(k)-yout(k);%计算当前误差de(k)=(e(k)-e_1)/ts; %计算u(k)中微分项输出u(k)=20.0*e(k)+0.50*de(k);%计算当前u(k)的输出%控制信号限幅if u(k)>10.0u(k)=10.0;endif u(k)<-10.0u(k)=-10.0;end%更新u(k-1)和e(k-1)u_1=u(k);e_1=e(k);endfigure(1);plot(time,rin,'r',time,yout,'b');%输入输出信号图xlabel('time(s)'),ylabel('rin,yout');figure(2);plot(time,rin-yout,'r');xlabel('time(s)'),ylabel('error');%误差图程序运行结果显示表1所示。

安徽大学本科毕业论文（设计）（内封面）题目：数字PID控制算法仿真研究学生姓名：刘高文学号：院（系）：电子科学与技术学院专业：电气工程及其自动化入学时间：2006 年9月导师姓名：刘凯峰职称/学位：讲师/硕士导师所在单位：安徽大学电子科学与技术学院数字PID控制算法仿真研究安徽大学电子科学与技术学院 2006级电气工程及其自动化专业指导教师：刘凯锋安徽省合肥市 230601摘要PID 控制算法是过程控制中应用最广泛的一种控制方法。

PID 控制算法简单应用广泛, 但是其参数整定方法繁杂。

利用Matlab 可以方便地仿真, 实现PID 参数整定。

文章首先介绍了PID 控制算法的原理、框图和公式，通过MATLAB 仿真出普通增量式PID 控制算法引起系统输出不稳定的仿真图，并给出引起该系统不稳定的原因，最后，文章研究了现实中应用较为广泛的BP神经网络PID控制，并与普通PID控制进行了对比研究。

关键词：PID控制；不完全微分;智能控制；神经网络Simulation Study on Digital PID ControlAbstractPID control algorithm is the most widely methods used in process control. PID control algorithm is simple and widely used，but its parameter setting method is multifarious. Matlab simulation can be easily realized PID parameters setting. This paper firstly introduces the principle of PID control algorithm, through the block diagram and formula MATLAB simulation of an ordinary incremental PID control algorithm cause instability of the simulation system, and gives the figure of instability.Finally，the paper studies the BP neural network PID control which has a wide use in reality and then compared with ordinary PID control.network0、引 言在模拟控制系统中,系统的控制器是连续模拟环节,亦称模拟调节器.而在数字控制系统中,则用数字控制器来代替模拟调节器,其直接控制过程是首先通过对模拟量输入通道对控制参数进行采样,并将其转换成数字量,然后计算机按一定的控制算法进行运算处理,计算结果由模拟量输出通道输出,并通过执行机构去控制生产过程,已达到预期的效果.这里,计算机执行按某种算法编写的程序,实现对被控制对象的控制和调节,被称为数字控制器。

离散控制系统中的PID控制器设计PID控制器是一种常用的控制器，广泛应用于离散控制系统中。

它是由比例项（P项）、积分项（I项）和微分项（D项）三个部分组成的，通过对系统的反馈信号进行处理，以使得系统响应更加稳定和准确。

在离散控制系统中，PID控制器的设计十分关键。

合理地设置PID 参数是实现良好控制效果的关键。

下面将基于离散控制系统中的PID 控制器设计，详细讨论PID参数的选择方法与调整策略。

一、PID参数的选择方法PID控制器的性能取决于其参数的选择，而PID参数的选择可以采用以下几种常用的方法：1. 经验法：根据经验公式或者实际应用中的调试经验，直接选取PID参数。

由于经验法灵活性较大，但不够科学，容易导致控制效果不理想。

2. Ziegler-Nichols方法：该方法基于系统的频域特性进行参数的调整，步骤较为简单。

首先，将控制器的I、D项参数设为0，只保留P 项；然后逐步增加P项增益，直至系统产生持续性振荡；最后按照振荡周期调整P、I、D项参数。

3. 优化算法：如遗传算法、粒子群算法等，通过优化算法求解PID 参数的最优取值。

该方法需要有系统的数学模型作为基础，且需要足够多的计算资源支持。

以上是几种常用的PID参数选择方法，不同的方法适用于不同的情况。

在具体选择过程中，需要从实际需求和系统特点出发，综合考虑，选择适合的方法。

二、PID参数的调整策略PID参数的调整是为了使得控制系统更加稳定和准确，常用的调整策略包括参数整定法和自整定法两种：1. 参数整定法：该方法是根据系统的动态性能指标，通过试探和修正的方式进行PID参数的调整。

常用的动态性能指标包括超调量、调整时间、稳态误差等。

根据实验结果，逐步修正PID参数，直至满足系统的性能要求。

2. 自整定法：自整定法是指采用自适应控制算法，通过系统自身的响应来动态调整PID参数。

常用的自整定算法有基于模型的自整定方法、经验模型自调整控制（EMC）方法等。