《平行线和相交线》周清2

第五章 相交线与平行线周清测试题班级 姓名 分数一、选择题（每小题4分，共32分）1．如果α∠=400，那么α∠的补角是（ ）（A ） 500 （B ）600 （ C ）1400 （D ）1600 2．两条平行线被第三条直线所截，不一定相等的角是（ ）（A ） 对顶角 （B ）内错角 （C ）同位角 （D ）同旁内角3．如图1所示，直线AB ，CD 相交于点O ，OE ⊥AB ，那么下列结论错误的是（ ）.图1 图2（A ）∠AOC 与∠COE 互为余角 （B ）∠BOD 与∠COE 互为余角 （C ）∠COE 与∠BOE 互为补角 （D ）∠AOC 与∠BOD 是对顶角 ４．如图2，下列说法不正确的是（ ）．（A ）∠1与∠2是同位角 （B ）∠2与∠3是同位角 （C ）∠1与∠3是同位角 （D ）∠1与∠4是内错角 5．如图3所示，下列条件中，不能得到AB ∥CD 的是（ ） （A ）∠A+∠ADC=180° （B ）∠3=∠1 （C ）∠ABC+∠C=180° （D ）∠2=∠46．根据图4与已知条件，指出下列推断错误的是（ ）（A ）由∠1=∠2，得AB ∥CD （B ）由∠1+∠3=∠2+∠4，得AE ∥CN （C ）由∠5=∠6，∠3=∠4，得AB ∥CD （D ）由∠SAB=∠SCD ，得AB ∥CD7．如图5所示，要得到DE ∥BC ，则需要条件（ ）（A ）∠AED= ∠4 （B ）∠4+∠5=180° （C ）∠1=∠3 （D ）∠2=∠38．如图6所示，已知∠1=∠2，若要证∠3=∠4，则需要（ ）（A ）∠1=∠3 （B ）∠2=∠3 （C ）AB ∥CD （D ）∠1=∠4AB E F SCG N D) ) ) ) ) ) 13 5 24 6 图4 A B CD F GE( ) ( ) (12 3 4 5 图5 A B E CFD) ) ( ( 1 3 2 4 图6a b c 21 ) (图7ABCD1 2) (图8O ABCD1 2 3 4)) ( (图3二、填空题（每小题4分，共28分）9．如图7所示，已知a ∥b ，∠2=135°，则∠1= ．10．如图8，点O 在直线AB 上，OC ⊥OD ，若∠1=50°，则∠2= ．11．如图9所示，AG ∥BC ，∠A=∠1，CE ⊥AB ，则∠DCE= ． 12．如图10，AB ∥EF ∥CD ，∠A=72°，∠D=18°，则AE 与DE 的位置关系是 ．图9 图10 图1113．如图11，已知∠B+∠C ＝180°，则∠1与∠2的大小关系为∠1_____∠2（填<、>、＝） 14．如图12已知AB||CD ，BE 平分∠ABC, ∠CDE=1500,则∠C= ．图12 图1315．如图13，直线AB ∥CD ，EF ⊥AB ，垂足为O ，FG 与CD 相交于H ，若∠1=43°，则∠2= ． 三、解答题（本大题共40分）16、(18分)已知：如图14 ，AB ∥CD ，EF 交AB 于G ，交CD 于F ，FH 平分∠EFD ，交AB 于H ，∠AGE=500，求：∠BHF 的度数．图14 17．（22分）如图15， E 在直线DF 上，B 在直线AC 上，若∠AGB=∠EHF ，∠C=∠D ，试判断∠A 与∠F 的关系，并说明理由。

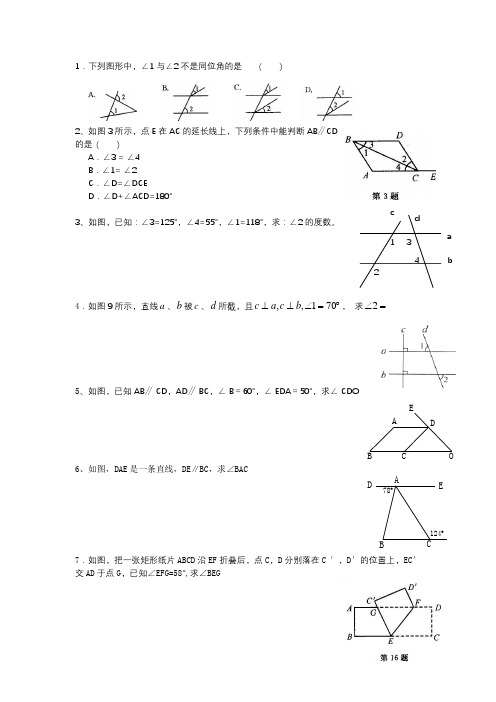
1．下列图形中，∠1与∠2不是同位角的是()2、如图3所示，点E在AC的延长线上，下列条件中能判断AB∥CD的是( )A．∠3 = ∠4B．∠1= ∠2C．∠D=∠DCED．∠D+∠ACD=180°3、如图，已知：∠3=125°，∠4=55°，∠1=118°，求：∠2的度数。

4．如图9所示，直线a、b被c、d所截，且︒=∠⊥⊥701,,bcac，求=∠25、如图，已知AB∥ CD，AD∥ BC，∠ B＝60°，∠ EDA＝50°，求∠ CDO6、如图，DAE是一条直线，DE∥BC，求∠BAC7．如图，把一张矩形纸片ABCD沿EF折叠后，点C，D分别落在C ′，D′的位置上，EC′交AD于点G，已知∠EFG=58°,求∠BE G124︒78︒DCEBAOEDCBAadb1234c8、如图，AB ∥CD ，BF ∥CE ，则∠B 与∠C 有什么关系？请说明理由。

9、如图，AB ∥CD ，BE ∥CF 。

求证：∠1=∠4。

10、已知，如图，ＣＤ⊥ＡＢ，ＧＦ⊥ＡＢ，∠Ｂ＝∠ＡＤＥ。

试说明∠１＝∠２11、如图，CD∥AB，∠DCB=70°，∠CBF=20°，∠EFB=130°，问直线EF 与AB 有怎样的位置关系，为什么？12．如图，有一条直的宽纸带，按图折叠，求∠α的度数13.已知： AB ∥CD ，∠DCE ＝80°，求∠BEF 的度数F21GE DCBA14.直线AB 、CD 相交于点O ，OT ⊥AB 于O ，CE ∥AB 交CD 于点C ， 若∠ECO=30°，求∠DOT15.已知CD 平分∠ACD ，DE ∥AC ，∠1＝30°，求∠216、如图：已知；AB ∥CD ，AD ∥BC ，∠B 与∠D 相等吗？试说明理由．17、如图，∠1=100°，∠2=100°，∠3=120°，求∠418、在△ABC 中，∠A=80°，∠B=30°，CD 平分∠ACB ，DE ∥AC1）求∠DEB 的度数；2）求∠EDC 的度数19、如图，∠1+∠2=180°，∠DAE =∠BCF ，DA 平分∠BDF ． （1）AE 与FC 会平行吗?说明理由． （2）AD 与BC 的位置关系如何?为什么? （3）BC 平分∠DBE 吗?为什么．D C B A F E21DCBAACD21a bm n4320、已知，如图13-2，∠1＝∠2，CF ⊥AB ，DE ⊥AB ，说明：FG ∥BC 。

O DCBA 第五周 数学周周清姓名 _____________ 班级 ____________ 等级 _____________一、选择题:1.下列计算正确的是（ ）．A ．22a a -=B ．623m m m ÷= C ．2008200820082xx x += D ．236t t t ⋅=2．在下列多项式的乘法中，可用平方差公式计算的是（ ）A ．(2＋a)(a ＋2)B ．(21a ＋b)(b －21a) C ．(－x ＋y)(y －x)D ．(x 2＋y)(x －y 2)3．老师给出：1a b += ，222a b +=，你能计算出ab 的值为 （ ）． A ．1- B ．3 C ．32- D ．12-4．要使式子22259y x +成为一个完全平方式，则需加上( ) ． A ．xy 15 B ．xy 15± C ．xy 30 D ．xy 30±5．要使等式22)()(b a M b a +=+-成立，代数式M 应是( ) ． A ．ab 2 B ．ab 4 C ．ab 4- D ．ab 2- 6 .如图1所示,下列说法不正确的是( )A.点B 到AC 的垂线段是线段AB;B.点C 到AB 的垂线段是线段ACC.线段AD 是点D 到BC 的垂线段;D.线段BD 是点B 到AD 的垂线段 7. 如图1所示,能表示点到直线(线段)的距离的线段有( )A.2条B.3条C.4条D.5条 图1 8. 如图2所示,AD ⊥BD,BC ⊥CD,AB=a cm, BC=b cm,则BD 的范围是( ) A.大于a cm B.小于b cmC.大于a cm 或小于b cmD.大于b cm 且小于a cm图2 二、填空题:1. a 2－6a+_____=（a －3）2；(x-3)(x+3)=______； 2 0 + 2－1 =_____； （－0.5）2007×22009 =2.澳洲科学家称他们发现全世界最小、最轻的鱼，取名为胖婴鱼。

2024北师大版数学七年级下册第二章《平行线与相交线》教学设计一. 教材分析《平行线与相交线》是北师大版数学七年级下册第二章的内容。

本章主要介绍了平行线与相交线的概念、性质以及它们之间的关系。

通过本章的学习，使学生能够理解并掌握平行线与相交线的性质，能够运用它们解决实际问题。

教材内容安排合理，循序渐进，通过大量的例子和练习题，帮助学生巩固所学知识。

二. 学情分析面对刚进入七年级的学生，他们对平面几何的基础知识有一定的了解，但还需要进一步的巩固和提高。

在学习本章内容时，学生需要具备一定的观察能力、逻辑思维能力和空间想象力。

同时，学生应该具备良好的学习习惯和合作意识，能够主动参与课堂讨论和实践活动。

三. 教学目标1.知识与技能：使学生掌握平行线与相交线的概念和性质，能够运用它们解决实际问题。

2.过程与方法：通过观察、操作、思考、交流等过程，培养学生的观察能力、逻辑思维能力和空间想象力。

3.情感态度与价值观：激发学生对数学的兴趣和好奇心，培养学生的合作意识和创新精神。

四. 教学重难点1.教学重点：平行线与相交线的概念、性质及其应用。

2.教学难点：平行线与相交线的判断和证明。

五. 教学方法采用问题驱动法、案例教学法、合作学习法等多种教学方法。

通过引导学生观察、思考、交流，激发学生的学习兴趣，培养学生的自主学习能力。

六. 教学准备1.教学素材：准备相关的图片、例子、练习题等教学素材。

2.教学工具：准备黑板、粉笔、多媒体教学设备等教学工具。

3.学生活动：提前学生进行预习，了解平行线与相交线的基本概念。

七. 教学过程1.导入（5分钟）通过展示一些生活中的图片，如街道、铁路等，引导学生观察并思考这些图片中包含了哪些几何图形。

进而引出平行线与相交线的概念。

2.呈现（10分钟）利用多媒体教学设备，展示平行线与相交线的定义和性质。

通过具体的例子，使学生理解并掌握平行线与相交线的概念。

3.操练（10分钟）学生分组进行实践活动，每组选择一道与平行线与相交线相关的题目进行解答。

第1页第五章《相交线与平行线》单元测试题一、选择题：（每小题3分，共33分）1、同一平面内，三条直线相交的交点个数为（ ）A ．0个或1个 B.1个或2个 C.2个或3个 D.0个或1个或2个或3个2、一副三角扳按如图1方式摆放，且∠1的度数比∠2的度数大54°，则∠1＝9）A ． 18°B ．54°C ．72°D ．70°3. 如图2，下列条件中，不能判断直线ｌ１∥ｌ２的是（ ）Ａ.∠１＝∠３ Ｂ.∠４＝∠５ Ｃ.∠２＋∠４＝180° Ｄ.∠２＝∠３4. 如图3，ＡＢ∥ＣＤ∥ＥＦ，ＡＦ∥ＣＧ，则图中与∠Ａ（不包括∠Ａ）相等的角有（ ）Ａ.５个 Ｂ.４个 Ｃ.３个 Ｄ.２个5、点P 为直线l 外一点，点A 、B 、C 为直线l 上三点，PA = 4 cm ，PB = 5 cm ，PC = 2 cm ，则点到直线l 的距离是（ ）A 、2cmB 、小于2cmC 、不大于2cmD 、不小于2cm 6. 下列各命题中，是真命题的是（ ）（A ）同位角相等 （B ）内错角相等 （C ）邻补角相等 （D ）对顶角相等7. 如图，点D 在直线AE 上，量得∠CDE=∠A=∠C ，有以下三个结论：①AB ∥CD ；②AD ∥BC ；③∠B=∠CDA . 则正确的结论是（ ）（A ）①②③ （B ）①② （C ）① （D ）②③8．如下图，CD AB //，且 25=∠A ， 45=∠C ，则E ∠的度数是（ ）A. 60B. 70C. 110D. 80图2图1图3AB CD（第10题）ED CBAA B C DE F（第9题）第2页9. 如图，将周长为8的三角形ABC 向右平移1个单位后得到三角形DEF ，则四边形ABFD 的周长等于 .10. 一个小区大门的栏杆如图所示，BA 垂直地面AE 于A ，CD 平行于地面AE ，那么∠ABC ＋∠BCD= 度.11如图所示，已知12∠=∠，要使34∠=∠，则需（ ）（A ）13∠=∠ （B ）24∠=∠ （C ）14∠=∠ （D ）AB ∥CD二、填空题（每小题3分，共24分） 12、下面生活中的物体的运动情况可以看成平移的是_______________________。

aC 课题：5.2.1平行线【学习目标】1.了解平行线的概念、平面内两条直线的相交和平行的两种位置关系, 知道平行公理以及平行公理的推论.2.会用符号语言表示平行公理推论, 会用三角尺和直尺过已知直线外一点画这条直线的平行线.【学习重点】探索和掌握平行公理及其推论.【学习难点】对平行线本质属性的理解,用几何语言描述图形的性质.【学前准备】分别将木条a 、b 与木条c 钉在一起,做成图示的教具. 【问题探索】1.两条直线相交有几个交点?相交的两条直线有什么特殊的位置关系? 2，在平面内,两条直线除了相交外,还有别的位置关系吗?的两条横及格本中两条横线，若把他们向两方延长，看成直线，线吗？34．自我演示.顺时针转动木条b 两圈,然后思考:把a 、b 想像成两端可以无限延伸的两条直线,顺时针转动b 时,直线b 与直线a 的交点位置将发生什么变化?在这个过程中, 有没有直线b 与a 不相交的位置?5.同学交流并形成共识.转动b 时,直线b 与c 的交点从在直线a 上A 点向左边距离A 点很远的点逐步接近A 点,并垂合于A 点,然后交点变为在A 点的右边,逐步远离A 点.继续转动下去,b 与a 的交点就会从A 点的右边又转动A 点的左边……可以想象一定存在一个直线b 的位置,它与直线a 左右两旁都 如下图cb a【自主学习】---平行线定义、表示法1.结合演示的结论,用自己的语言描述平行线的认识:①平行线是同一 的两条直线②平行线是 交点的两条直线2．尝试用数学语言描述平行定义特别注意：直线a 与b 是平行线,记作“ ”,这里“ ”是平行符号.思考： 如何确定两条直线的位置关系？.【合作探究】----画图、观察、探索平行公理及平行公理推论1.在转动教具木条b 的过程中,有几个位置能使b 与a 平行?2.用直线和三角尺画平行线. 已知:直线a,点B,点C.(1)过点B 画直线a 的平行线,能画几条?(2)过点C 画直线a 的平行线,它与过点B 的平行线平行吗? b3.观察画图、归纳平行公理及推论.(1)对照垂线的第一性质说出画图所得的结论.平行公理:(2)比较平行公理和垂线的第一条性质.共同点:都是“ ”,这表明与已知直线平行或垂直的直线存在并且是 的.不同点:平行公理中所过的“一点”要在已知直线 ,两垂线性质中对“一点”没有限制,可在直线 ,也可在直线 .4.探索平行公理的推论. (1)直观判定过B 点、C 点的a 的平行线b 、c 是互相 . (2)从直线b 、c 产生的过程说明直线b ∥直线c.(3)用三角尺与直尺用平推方法验证b ∥c. (4)用数学语言表达这个结论用符号语言表达为:如果 那么(5)简单应用. 将一张长方形纸片对折两次，得到三条折痕，这三条折痕有什么关系，请说明理由。