八年级下册数学周周清试卷3

1. 已知方程x² - 5x + 6 = 0 的两个根分别为 x₁和 x₂，则 x₁ + x₂等于（）A. 2B. 5C. 6D. 12. 若a² = 4，b² = 9，则 |a| + |b| 等于（）A. 5B. 6C. 7D. 83. 在直角坐标系中，点 P（2，3）关于 x 轴的对称点坐标为（）A.（2，-3）B.（-2，3）C.（-2，-3）D.（2，-3）4. 已知 a、b、c 成等差数列，且 a + b + c = 12，则 b 的值为（）A. 4B. 6C. 8D. 105. 在△ABC中，∠A = 30°，∠B = 45°，则∠C 的度数为（）A. 45°B. 60°C. 75°D. 90°6. 已知一次函数 y = kx + b 的图象经过点（2，3），则该函数的斜率 k 等于（）A. 1B. 2C. 3D. 47. 已知二次函数y = ax² + bx + c 的图象开口向上，且 a > 0，则该函数的顶点坐标为（）A.（-b/2a，c - b²/4a）B.（b/2a，c - b²/4a）C.（-b/2a，c + b²/4a）D.（b/2a，c + b²/4a）8. 若 a、b、c 成等比数列，且 a = 2，b = 4，则 c 的值为（）A. 8B. 6C. 3D. 19. 在等腰三角形 ABC 中，底边 BC 的长度为 4，腰 AB = AC = 6，则三角形 ABC 的面积为（）A. 12B. 18C. 24D. 3010. 若x² - 2x + 1 = 0，则 x 的值为（）A. 1B. 2C. 3D. 411. 若m² - 3m + 2 = 0，则 m 的值为________。

12. 已知 a、b、c 成等差数列，且 a + b + c = 12，则 b 的值为________。

第 1 页 /共 2 页2020-2021学年八年级（下）第十次周清数学测试卷（周测内容：19.2.1正比例函数、19.2.2一次函数）2021年5月30日 一.选择题（每题4分，共36分）1.若y=(m-1)x+m 2-1是y 关于x 的正比例函数,则该函数图象经过的象限是( )A. 第一、三象限B. 第二、四象限C. 第一、四象限D. 第二、三象限2.若一次函数y=(k-2)x+1的函数值y 随x 的增大而增大，则A. B. C. D.3.如图，两直线y 1=kx+b 和y 2=bx+k 在同一坐标系内图象的位置可能是A. B. C. D.4.一次函数y=kx+3(k ≠0)的函数值y 随x 的增大而增大，它的图象不经过的象限是A. 第一B. 第二C. 第三D. 第四5.已知点M （1,a ）和点N （3,b ）是一次函数y = 2x +1图象上的两点，则a 与b 的大小关系是（ ）A. a ＞bB. a =bC. a ＜bD. 无法确定6.关于一次函数y=5x-3的描述，下列说法正确的是（ ）A. 图象经过第一、二、三象限B. 向下平移3个单位长度，可得到y=5xC. 函数的图象与x 轴的交点坐标是(0,-3)D. 图象经过点(1,2)7.如图是一次函数y =kx +b 的图象，则一次函数的解析式是（ ）A. y =-4x +3B. y =4x +3C. y =43x +3D. y =-43x +3 8.已知一次函数y 1=bx+1与一次函数y 2=-x+b 关于y 轴对称，若点A 是函数y 1图象与x 轴的交点,则点A 的坐标是（ ）A. （1，0）B. （-1，0）C. （0，-1）D. （0，1）9.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息．已知甲先出发4分钟在整个步行过程中，甲、乙两人的距离y(米)与甲出发的时间t(分钟)之间的关系如图所示，下列结论：甲步行的速度为60米/分钟；乙用16分钟追上甲；乙走完全程用了30分钟；乙到达终点时甲离终点还有360米；其中正确的结论有A. 1个B. 2个C. 3个D. 4个二.填空题（每题4分，共28分）10.若y =(k +1)x |k |+4是一次函数，则k = ______ ．11.将函数y =的图象向上平移 ______ 个单位后，所得图象经过点（0，1）．12.点A(x 1 ,y 1)、B(x 2 ,y 2)在一次函数y=-2x+b 的图象上，若x 1<x 2，则y 1 ______ y 2( 填“<”或“>”或“=”)．13.请你写出一个一次函数，使它经过二、三、四象限 ______ ．14.如图，若点P （-2，4）关于y 轴的对称点在一次函数y =x +b 的图象上，则b 的值为 ______ ．15.已知直线y =kx +b （k ≠0）与直线y =-3x 平行，且与两坐标轴围成的三角形的面积为6，那么这条直线的解析式为 ______ ．姓名： 班级：16.如图，购买“黄金1号”王米种子，所付款金额y元与购买量x（千克）之间的函数图象由线段OA和射线AB组成，则购买1千克“黄金1号”玉米种子需付款 ______ 元，购买4千克“黄金1号”玉米种子需 ______ 元．三.解答题（共3题，共36分）17.（12分）已知y=y1+y2,y1与(x-1)成正比例，y2与(x+1)成正比例，且当x=0时，y=-3；当x=1时，y=-2.（1）求y的函数解析式. （2）求直线y与两坐标轴围成的三角形的面积.18.（12分）如图，直线l1、l2相交于点A，求点A的坐标.19.（12分）如图,在平面直角坐标系中,过点B(6,0)的直线AB与某正比例函数图象相交于点A(4,2).(1)求直线AB的解析式.(2)求△OAC的面积.第2页/ 共2页。

初中数学试卷马鸣风萧萧六盘水市第十三中学八年级下数学第二次周周清（C ）班级： 姓名： 得分：二、填空：（每空5分）1、等边三角形的三个内角都 ，并且每个角都等于 。

2、直角三角形全等的判定方法有五个：SSS 、 、 、 及 。

3、命题“全等三角形的对应边相等”的逆命题是 ，它们 （填“是”或“不是”）逆定理。

三、已知：在△ABC 中，AB=AC=2a,∠ABC=∠ACB=15°，CD 是腰AB 上的高，求CD 的长。

（20分）四、已知∠ACB = ∠ADB = 90°，AC = AD ，E 是AB 上的一点。

求证：CE = DE （20分）C B AD EDB CA六盘水市第十三中学八年级下数学第二次周周清（C ）班级： 姓名： 得分：一、选择：（每题10分）1、下列命题写成逆命题后，两者是互逆定理的是（ ）A ． 全等三角形的对应角相等 B. 两直线平行，内错角相等 C ． 对顶角相等 D. 若a =b ，则b a2、等腰三角形补充下列条件后，仍不一定成为等边三角形的是（ ） A.有一个内角是60° B.有一个外角是120° C.有两个角相等 D.腰与底边相等二、填空：（每空5分）1、等边三角形的三个内角都 ，并且每个角都等于 。

2、直角三角形全等的判定方法有五个：SSS 、 、 、 及 。

3、命题“全等三角形的对应边相等”的逆命题是 ，它们 （填“是”或“不是”）逆定理。

三、已知：在△ABC 中，AB=AC=2a,∠ABC=∠ACB=15°，CD 是腰AB 上的高，求CD 的长。

（20分）四、已知∠ACB = ∠ADB = 90°，AC = AD ，E 是AB 上的一点。

求证：CE = DE （20分）C BADED B CA。

2012年春2013级数学第三周周清练习题班级 姓名 学号一、 选择题（每题3分，共计9分）1、分式31x ax +-中，当x ＝-a 时，下列结论正确的是（ ）A ．分式的值为零；B ．分式无意义C ．若a ≠-13时，分式的值为零； D ．若a ≠13时，分式的值为零 2、下列各分式中，最简分式是（ ）A 、()()y x y x +-8534 B 、y x x y +-22 C 、2222xy y x y x ++ D 、()222y x y x +- 3、分式214x -，42xx-的最简公分母为（ ） A ．（x+2）（x-2） B ．-2（x+2）（x-2） C ．2（x+2）（x-2） D ．-（x+2）（x-2） 二、化简、（每小题6分，共24分）1、 2333222⎪⎭⎫ ⎝⎛∙÷⎪⎪⎭⎫ ⎝⎛-a c d a cd b a 2、q mnpmn q p pq n m 3545322222÷∙3、228241681622+-∙+-÷++-a a a a a a a . 4、3234223362⎪⎭⎫ ⎝⎛-∙÷⎪⎪⎭⎫ ⎝⎛-b c b a d c ab .三、计算题（每小步骤2分，共58分） 1、21a -+21(1)a - 2、qp q p 321321-++解：最简公分母为： 解：最简公分母为：21a -==+qp 32121(1)a -==-q p 321∴原式= ∴原式= 3、2129m -+23m -+23m + 4、222x x x +--2144x x x --+ 解：最简公分母为： 解：最简公分母为：2129m -= 222x x x +-=23m -= 2144x x x --+= 23m += ∴原式= ∴原式=5、4122b b a b a b a ÷--∙⎪⎭⎫⎝⎛ 6、x y yx x y y x 222222÷-∙⎪⎪⎭⎫ ⎝⎛ 解：①22⎪⎪⎭⎫ ⎝⎛b a = 解：①=⎪⎪⎭⎫⎝⎛22y x②=-∙⎪⎪⎭⎫ ⎝⎛b a b a 122②=∙⎪⎪⎭⎫ ⎝⎛x y y x 222③=÷4b b a ③=÷x y yx 222原式= 原式=7、⎪⎪⎭⎫⎝⎛+---⎪⎪⎭⎫ ⎝⎛+∙+11111212x x x x x x 8、先化简，后求值： （212x x -－2144x x -+）÷222x x - 解：①=⎪⎪⎭⎫ ⎝⎛+212x x 请选择一个自己认为合适的值代入计算。

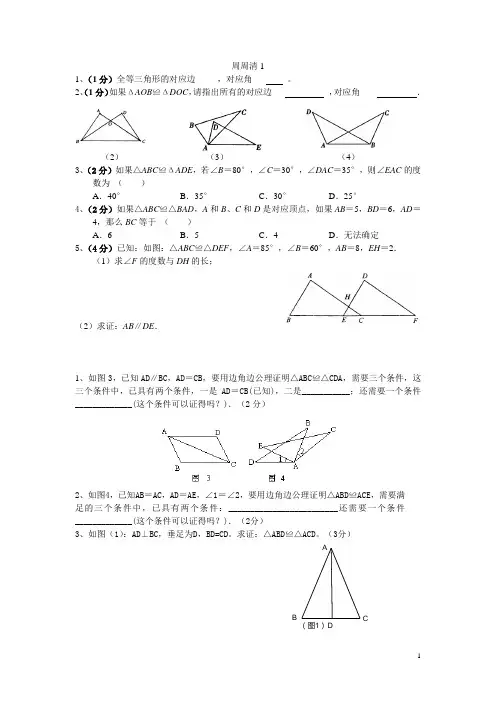
周周清11、（1分）全等三角形的对应边_____，对应角____ _。

2、（1分）如果ΔAOB ≌ΔDOC ，请指出所有的对应边___ _，对应角____ _．（2） （3） （4）3、（2分）如果△ABC ≌ΔADE ，若∠B ＝80°，∠C ＝30°，∠DAC ＝35°，则∠EAC 的度数为 （ ）A ．40°B ．35°C ．30°D ．25°4、（2分）如果△ABC ≌△BAD ，A 和B 、C 和D 是对应顶点，如果AB ＝5，BD ＝6，AD ＝4，那么BC 等于 （ ）A ．6B ．5C ．4D ．无法确定5、（4分）已知：如图：△ABC ≌△DEF ，∠A ＝85°，∠B ＝60°，AB ＝8，EH ＝2．（1）求∠F 的度数与DH 的长；（2）求证：AB ∥DE ．1、如图3，已知AD ∥BC ，AD ＝CB ，要用边角边公理证明△ABC ≌△CDA ，需要三个条件，这三个条件中，已具有两个条件，一是AD ＝CB(已知)，二是___________；还需要一个条件_____________(这个条件可以证得吗？)．（2分）2、如图4，已知AB ＝AC ，AD ＝AE ，∠1＝∠2，要用边角边公理证明△ABD ≌ACE ，需要满足的三个条件中，已具有两个条件：_________________________还需要一个条件_____________(这个条件可以证得吗？)．（2分）3、如图（1）：AD ⊥BC ，垂足为D ，BD=CD 。

求证：△ABD ≌△ACD 。

（3分）（图1）D C B A4、如图（2）：AC ∥EF ，AC=EF ，AE=BD 。

求证：△ABC ≌△EDF 。

（3分）1、 填空（2分）判定两个三角形全等的方法有， 。

（用字母表示）2如图2，O 是AB 的中点， 要使通过角边角（ASA ）来判定△OAC ≌△OBD ，需要添加一个如条件,下列条件正确的是( ） (2分)A 、∠A=∠B B 、AC=BDC 、∠C=∠D2、已知点D 在AC 上，点E 在AB 上，CE 和BD 相交于点O ，AB=AC,∠B=∠C,求证：BE=CD （3分）1、（2分）只允许用 的直尺和 作图，这类问题叫做尺规作图。

检测内容：1.1－1.2得分________卷后分________评价________一、选择题(每小题5分，共35分)1．如图，a∥b，点A在直线a上，点C在直线b上，∠BAC＝90°，AB＝AC，若∠1＝20°，则∠2的度数为(B)A．25°B．65°C．70°D．75°第1题图第3题图2．在△ABC中，a，b，c分别是∠A，∠B，∠C的对边．若(a－2)2＋b－2＋|c－22 |＝0，则此三角形是(A)A．等腰直角三角形B．直角三角形C．等腰三角形D．钝角三角形3．如图，在△ABC中，AB＝AC，∠A＝36°，BD，CE分别是△ABC，△BCD的角平分线，则图中的等腰三角形有(A)A．5个B．4个C．3个D．2个4．某市在旧城改造中，计划在一块如图所示的△ABC空地上种植一草皮以美化环境，已知∠A＝150°，这种草皮每平方米售价a元，则购买这种草皮至少需要(B)A.300a元B．150a元C．450a元D．225a元5．等腰三角形一腰上的高与另一腰的夹角为20°，则顶角的度数是(C)A．70°B．110°C．70°或110°D．20°或160°6．如图，点A，B，C在同一条直线上，△ABD，△BCE均为等边三角形，连接AE 和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM, 则∠DMA的度数为(B)A．45°B．60°C．75°D．90°第6题图第7题图7．如图，∠AOB ＝120°，OP 平分∠AOB ，且OP ＝2.若点M ，N 分别在OA ，OB 上，且△PMN 为等边三角形，则满足上述条件的△PMN 有(D)A ．1个B ．2个C ．3个D ．3个以上二、填空题(每小题5分，共20分)8．命题“两条直线相交只有一个交点”的逆命题是__只有一个交点的两条直线一定相交__，它是__真__命题．9．如图，在△ABC 中，AB ＝AC ，AD ，CE 是三角形的高，垂足为D ，E ，若∠CAD ＝20°，则∠BCE ＝__20°__．第9题图第10题图10．如图，在Rt △ABC 中，∠C ＝90°，点D 在线段BC 上，且∠B ＝30°，∠ADC ＝60°，BC ＝3，则BD 的长度为__2__．11．在△ABC 中，AB ＝22 ，BC ＝1，∠ABC ＝45°，以AB 为边作等腰直角三角形ABD ，使∠ABD ＝90°，连接CD ，则线段CD 的长为．三、解答题(共45分)12．(8分)如图，AC ⊥BC ，BD ⊥AD ，AC ，BD 相交于点O ，AC ＝BD .(1)求证：BC ＝AD ；(2)求证：△OAB 是等腰三角形．证明：(1)∵AC ⊥BC ，BD ⊥AD ，∴∠D ＝∠C ＝90°，在Rt △ADB 与Rt △BCA 中，⎩⎪⎨⎪⎧AB ＝BA ，AC ＝BD ， ∴Rt △ABD ≌Rt △BAC (HL)，∴BC ＝AD (2)由(1)得，∠DBA ＝∠CAB ，∴OA ＝OB ，即△OAB 是等腰三角形13．(12分)如图，△ABC 为等边三角形，∠1＝∠2＝∠3.(1)求∠BEC 的度数；(2)△DEF 是等边三角形吗？请说明理由．解：(1)∠BEC＝∠ADE＋∠DFE＝∠ABD＋∠2＋∠CAF＋∠1＝∠ABC＋∠BAC＝60°＋60°＝120°(2)是等边三角形．理由：由(1)知∠DEF＝180°－120°＝60°.同理∠EDF＝∠DFE＝60°，∴△DEF是等边三角形14．(12分)如图，把长方形纸片ABCD沿EF折叠，使点B落在边AD上的点B′处，点A落在点A′处．(1)求证：B′E＝BF；(2)设AE＝a，AB＝b，BF＝c，试猜想a，b，c之间的一种关系，并给予证明．解：(1)证明：由题意得B′F＝BF，∠B′FE＝∠BFE.又∵AD∥BC，∴∠B′EF＝∠BFE，∴∠B′FE＝∠B′EF，∴B′F＝B′E，∴B′E＝BF(2)a，b，c的关系为a2＋b2＝c2，连接BE，则BE＝B′E，由(1)知B′E＝BF＝c，∴BE＝c.∵AE2＋AB2＝BE2，又∵AE＝a，AB＝b，∴a2＋b2＝c2(若写a＋b>c也可以)15．(13分)(1)操作发现：如图①，D是等边三角形ABC边BA上一动点(点D与点B 不重合)，连接DC，以DC为边在BC上方作等边三角形DCF，连接AF.你能发现AF与BD之间的数量关系吗？并证明你发现的结论；(2)类比猜想：如图②，当动点D运动至等边三角形ABC边BA的延长线上时，其他作法与(1)相同，猜想AF与BD在(1)中的结论是否仍然成立？(3)深入探究：如图③，当动点D在等边三角形ABC边BA上运动时(点D与点B不重合)，连接DC，以DC为边在BC上方，下方分别作等边三角形DCF和等边三角形DCF′，连接AF，BF′，探究AF，BF′与AB有何数量关系？并证明你探究的结论．解：(1)AF＝BD，证明△ACF≌△BCD(SAS)(2)仍成立(3)AF＋BF′＝AB，证明：由(1)知，AF＝BD，易证△ACD≌△BCF′(SAS)，∴BF′＝AD，∴AF＋BF′＝BD＋AD＝AB。

八年级数学第三周周清试卷2012年春2013级数学第三周周清练习题班级 姓名 学号一、 选择题（每题3分，共计9分）1、分式31x ax +-中，当x ＝-a 时，下列结论正确的是（ ） A ．分式的值为零； B ．分式无意义C ．若a ≠-13时，分式的值为零；D ．若a ≠13时，分式的值为零2、下列各分式中，最简分式是（ ）A 、()()y x y x +-8534 B 、y x x y +-22 C 、2222xy y x y x ++ D 、()222y x y x +-3、分式214x -，42xx-的最简公分母为（ ） A ．（x+2）（x-2） B ．-2（x+2）（x-2） C ．2（x+2）（x-2） D ．-（x+2）（x-2）二、化简、（每小题6分，共24分）1、 2333222⎪⎭⎫ ⎝⎛•÷⎪⎪⎭⎫ ⎝⎛-a c d a cd b a 2、q mnp mn q p pq n m 3545322222÷•3、228241681622+-•+-÷++-a a a a a a a . 4、3234223362⎪⎭⎫ ⎝⎛-•÷⎪⎪⎭⎫ ⎝⎛-b c b a d c ab .三、计算题（每小步骤2分，共58分） 1、21a -+21(1)a - 2、q p q p 321321-++ 解：最简公分母为： 解：最简公分母为：21a-==+q p 321 21(1)a -==-q p 321 ∴原式= ∴原式= 3、2129m -+23m -+23m + 4、222x x x +--2144x x x --+解：最简公分母为： 解：最简公分母为：2129m -= 222x x x +-= 23m -= 2144x x x --+= 23m += ∴原式= ∴原式=5、4122b b a b a b a ÷--•⎪⎭⎫ ⎝⎛6、x y y x x y y x 222222÷-•⎪⎪⎭⎫ ⎝⎛ 解：①22⎪⎪⎭⎫ ⎝⎛b a = 解：①=⎪⎪⎭⎫⎝⎛22y x②=-•⎪⎪⎭⎫ ⎝⎛b a b a 122②=•⎪⎪⎭⎫ ⎝⎛x y y x 222③=÷4b b a ③=÷x y y x 222原式= 原式=7、⎪⎪⎭⎫⎝⎛+---⎪⎪⎭⎫ ⎝⎛+•+11111212x x x x x x 8、先化简，后求值： （212x x -－2144x x -+）÷222x x-解：①=⎪⎪⎭⎫ ⎝⎛+212x x 请选择一个自己认为合适的值代入计算。

一、选择题（每题3分，共30分）1. 下列各数中，绝对值最小的是（）A. -3B. 2C. 0D. -52. 如果a > 0，b < 0，那么下列不等式中正确的是（）A. a > bB. a < bC. -a > -bD. -a < -b3. 下列函数中，图象是一条直线的是（）A. y = x^2B. y = 2x + 3C. y = √xD. y = x^34. 在直角三角形ABC中，∠C = 90°，AC = 3cm，BC = 4cm，那么AB的长度是（）A. 5cmB. 6cmC. 7cmD. 8cm5. 下列关于圆的命题中，正确的是（）A. 所有半径相等的圆都是同心圆B. 所有直径相等的圆都是同心圆C. 所有圆心在一条直线上的圆都是同心圆D. 所有圆周长相等的圆都是同心圆6. 如果一个正方形的对角线长度为6cm，那么这个正方形的边长是（）A. 3cmB. 4cmC. 5cmD. 6cm7. 下列各式中，正确的是（）A. (a + b)^2 = a^2 + b^2B. (a - b)^2 = a^2 - b^2C. (a + b)^2 = a^2 + 2ab + b^2D. (a - b)^2 = a^2 - 2ab + b^28. 下列各数中，是负数的是（）A. -√9B. -√4C. -√16D. -√259. 如果x^2 = 25，那么x的值是（）A. 5B. -5C. 5 或 -5D. 无法确定10. 下列关于二次函数的图象的说法中，正确的是（）A. 二次函数的图象一定是抛物线B. 二次函数的图象开口方向一定向上C. 二次函数的图象开口方向一定向下D. 二次函数的图象一定经过原点二、填空题（每题5分，共25分）11. 有理数a的相反数是______。

12. 在直角三角形中，如果一个角的正弦值是0.5，那么这个角的度数是______。

13. 如果一个圆的半径是r，那么这个圆的周长是______。

检测内容：18.1.1－18.1.2得分________卷后分________评价________一、选择题(每小题4分，共32分)1．下面的性质中，平行四边形不一定具有的是(A)A．对角互补B．邻角互补C．对角相等D．对边相等2．如图，▱ABCD的对角线AC，BD交于点O，已知AD＝8，BD＝12，AC＝6，则△OBC 的周长为(B)A．13 B．17 C．20 D．26,第2题图),第3题图) 3．如图，在▱ABCD中，∠ABC的平分线交AD于点E，∠BED＝150°，则∠A的大小为(C)A．150°B．130°C．120°D．100°4．如图，在四边形ABCD中，对角线AC，BD相交于点E，∠CBD＝90°，BC＝4，BE＝ED＝3，AC＝10，则四边形ABCD的面积为(D)A．6 B．12 C．20 D．24,第4题图),第5题图) 5．(2019·河池)如图，在△ABC中，D，E分别是AB，BC的中点，点F在DE延长线上，添加一个条件使四边形ADFC为平行四边形，则这个条件是(B)A．∠B＝∠F B．∠B＝∠BCFC．AC＝CF D．AD＝CF6．如图所示，在平行四边形ABCD中，EF∥BC，GH∥AB，EF，GH的交点P在BD 上，则图中面积相等的平行四边形有(B)A．平行四边形AEPG和平行四边形ABHGB．平行四边形AEPG和平行四边形PHCFC．平行四边形ABHG和平行四边形GPFDD．平行四边形GPFD和平行四边形AEPG,第6题图),第7题图) 7．(辽阳中考)如图，在▱ABCD中，∠BAD＝120°，连接BD，作AE∥BD交CD延长线于点E，过点E作EF⊥BC交BC的延长线于点F，且CF＝1，则AB的长是(B) A．2 B．1 C. 3 D. 28．(南阳内乡县期末)如图，AB∥CD，E，F分别为AC，BD的中点，若AB＝5，CD＝3，则EF的长是(D)A．4B．3C．2D．1二、填空题(每小题4分，共24分)9．如图，在▱ABCD中，E，F分别为AB，DC的中点，连接DE，EF，FB，则图中共有__4__个平行四边形．,第9题图),第10题图) 10．(十堰中考)如图，已知▱ABCD的对角线AC，BD交于点O，且AC＝8，BD＝10，AB＝5，则△OCD的周长为__14__．11．(2019·福建)在平面直角坐标系xOy中，▱OABC的三个顶点O(0，0)，A(3，0)，B(4，2)，则其第四个顶点是__(1，2)__．12．如图，在△ABC中，D，E分别是AB，AC的中点，F是BC延长线上的一点，FC ＝3，DF交CE于点G，且EG＝CG，则BC＝__6__．,第12题图),第14题图) 13．(2019·云南)在平行四边形ABCD中，∠A＝30°，AD＝43，BD＝4，则平行四边形ABCD的面积等于__163或83__．14．(武汉中考)如图，在△ABC中，∠ACB＝60°，AC＝1，D是边AB的中点，E是边BC上一点．若DE平分△ABC的周长，则DE的长是__32__．三、解答题(共44分)15．(10分)(卫辉市期末)如图，在平行四边形ABCD中，对角线AC＝21 cm，BE⊥AC，垂足为E ，且BE ＝5 cm ，AD ＝7 cm ，求AD 和BC 之间的距离．解：设AD 和BC 之间的距离为x ，则平行四边形ABCD 的面积等于AD·x ，∵S 平行四边行ABCD ＝2S △ABC＝2×12AC·BE ＝AC·BE ，∴AD ·x ＝AC·BE ，即7x ＝21×5，x ＝15(cm )．答：AD 和BC 之间的距离为15 cm16．(10分)(2019·广元)如图，已知在△ABC 中，∠BAC ＝90°，延长BA 到点D ，使AD ＝12AB ，点E ，F 分别是边BC ，AC 的中点．求证：DF ＝BE.证明：∵∠BAC ＝90°，∴∠DAF ＝90°.∵点E ，F 分别是边BC ，AC 的中点，∴AF ＝FC ，BE ＝EC ，FE 是△ABC 的中位线，∴FE ＝12AB ，FE ∥AB ，∴∠EFC ＝∠BAC ＝90°，∴∠DAF ＝∠EFC.∵AD ＝12AB ，∴AD ＝FE.在△ADF 和△FEC 中，⎩⎪⎨⎪⎧AD ＝FE ，∠DAF ＝∠EFC AF ＝FC ，，∴△ADF ≌△FEC(SAS )，∴DF ＝EC ，∴DF ＝BE17．(12分)(2019·遂宁)如图，在四边形ABCD 中，AD ∥BC ，延长BC 到E ，使CE ＝BC ，连接AE 交CD 于点F ，点F 是CD 的中点．求证：(1)△ADF ≌△ECF ；(2)四边形ABCD 是平行四边形．证明：(1)∵AD ∥BC ，∴∠DAF ＝∠E.∵点F 是CD 的中点，∴DF ＝CF. 在△ADF 与△ECF 中，⎩⎪⎨⎪⎧∠DAF ＝∠E ，∠AFD ＝∠EFC DF ＝CF ，，∴△ADF ≌△ECF(AAS ) (2)∵△ADF ≌△ECF ，∴AD ＝EC.∵CE ＝BC ，∴AD ＝BC.∵AD ∥BC ，∴四边形ABCD 是平行四边形18．(12分)(2019·安徽)如图，点E 在▱ABCD 内部，AF ∥BE ，DF ∥CE.(1)求证：△BCE ≌△ADF ；(2)设▱ABCD 的面积为S ，四边形AEDF 的面积为T ，求ST的值．解：(1)证明：∵四边形ABCD 是平行四边形，∴AD ＝BC ，AD ∥BC ，∴∠ABC ＋∠BAD ＝180°.∵AF ∥BE ，∴∠ABE ＋∠BAF ＝180°，∴∠CBE ＝∠DAF ，同理得∠BCE ＝∠ADF.在△BCE 和△ADF 中，∵⎩⎨⎧∠CBE ＝∠DAF ，BC ＝AD ，∠BCE ＝∠ADF ，∴△BCE ≌△ADF(ASA )(2)∵点E 在▱ABCD 内部，∴S △BEC ＋S △AED ＝12S ▱ABCD ，由(1)知△BCE ≌△ADF ，∴S △BCE ＝S △ADF ，∴S 四边形AEDF ＝S △ADF ＋S △AED ＝S △BEC ＋S △AED ＝12S ▱ABCD .∵▱ABCD 的面积为S ，四边形AEDF 的面积为T ，∴S T ＝S12S ＝2。

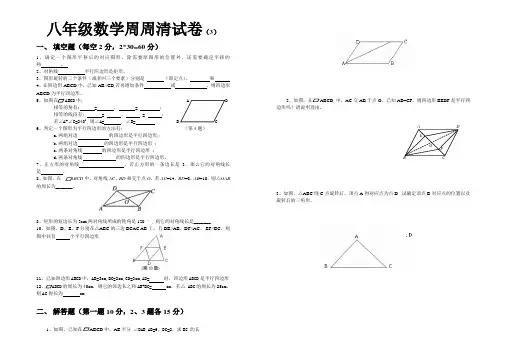
八年级数学周周清试卷（3）一、填空题（每空2分，2*30=60分）1、确定一个图形平移后的对应图形，除需要原图形的位置外，还需要确定平移的和。

2、对角线平行四边形是矩形。

3、图形旋转的三个条件（或者叫三个要素）分别是（即定点）、和4、在四边形ABCD中，已知AB//CD,若再增加条件或，则四边形ABCD为平行四边形。

5、如图在 ABCD中，相等的角有: = ， = ；相等的线段有： = ， =；若∠A+∠C=2400 ,则∠A= , ∠B= B C6、判定一个图形为平行四边形的方法有：（第4题）a.两组对边的四边形是平行四边形；b.两组对边的四边形是平行四边形；c.两条对角线的四边形是平行四边形；d.两条对角线的四边形是平行四边形。

7、正方形的对角线，若正方形的一条边长是3，那么它的对角线长是。

8、如图，在ABCD中，对角线AC、BD相交于点O，若AC=14，BD=8，AB=10，则△OAB的周长为_______．8、矩形的短边长为3cm,两对角线所成的钝角是120 °, 则它的对角线长是_______.10、如图，D、E、F分别在△ABC的三边BCAC.AB上，且DE//AB，DF//AC，,EF//BC，则图中共有个平行四边形11、已知四边形ABCD中，AB=3cm,BC=2cm,CD=3cm,AD= 时，四边形ABCD是平行四边形12ABCD的周长为40cm，则它的邻边长之和AB+BC= cm，若△ ABC的周长为25cm，则AC得长为 cm二、解答题（第一题10分，2、3题各15分）1、如图，已知在ABCD中，AE平分∠DAB,AB=6，BC=2，求EC的长.2、如图，在ABCD 中，AC交AB于点O，已知AE=CF，则四边形BEDF是平行四边形吗？请说明理由。

3、如图，△ABC绕C点旋转后，顶点A得对应点为点D. 试确定顶点B对应点的位置以及旋转后的三角形。

八年级数学下3月7日—15日周清试题题 号 一 二 三总分212223242526得 分一、相信你的选择(每小题3分，共33分)1、在直角三角形ABC 中，斜边AB=1，则AB 2+BC 2+AC 2的值 是（ ） A 、2 B 、4 C 、6 D 、82、如图，在△ABC 中，AB=AD=DC ，∠B=70°，则∠C 的度 数为（ ）A 、35° B 、40° C 、45° D 、50°3、如图所示，O 是∠BAC 内一点，且点O 到AB 、AC 的距离 OE=OF ，则△AEO ≌△AFO 的依据是（ ）A 、HLB 、AASC 、SSSD 、ASA4、如图，等腰△ABC 中，AB=AC,∠A=20°，线段AB 的垂直 平分线交AB 于D,交AC 于E ，连接BE,则∠CBE=（ ）A 、80°B 、70°C 、60°D 、50°5、用反证法证明“三角形中必有一个内角小于或等于60°”， 首先应假设这个三角形中（ ）A 、有一个内角大于60°B 、有一个内角小于60°C 、每一个内角都大于60°D 、每一个内角都小于60°6、下列命题①同旁内角互补，两直线平行；②全等三角形周长相等； ③直角都相等；④等边对等角。

它们的逆命题是真命题的个数是（ ）A 、1个B 、2个C 、3个D 、4个7、下列条件中，不能判断△ABC 为直角三角形的是（ ） A 、5.2,2,5.1===c b a B 、5:4:3::=c b a C 、C B A ∠=∠+∠ D 、5:4:3::=∠∠∠C B A8、如图△ABC 中，AB=5，AC=6，BC=4，边AB 的垂直平分线交AC 于 点D ，则△ABC 的周长是（ ）A 、8 B 、9 C 、10 D 、11ABC D FEB ACOEDC B A DEACB第2题图 第3题图 第4题图 第8题图9、如图，在△ABC 中，AB=AC ，∠A=36°，BD 、CE 分别是∠ABC 、∠BCD 的角平分线，则图中的等腰三角形有（ ） A 、5个 B 、4个 C 、3个 D 、2个10、如图折叠直角三角形纸片的直角，使点C 落在斜边AB 上的点E 处，CD=1，∠B=30°，则BD 的长是（ ）A 、1 B 、2 C 、3 D 、23 11、如图，AD 是△ABC 的角平分线，DF ⊥AB ，垂足为F ，△ADG 和△AED 的面积分别为50和39，则△EDF 的面积为（ ） A 、11 B 、5.5 C 、7 D 、3.5二、试试你的身手（每题4分，共24分）12、如图∠AOP =∠BOP=15°，PC ∥OA ，PD ⊥OA ，若PC=10，则PC= 。

一、选择题（每题3分，共30分）1. 若a，b是实数，且a + b = 0，则a与b互为（）A. 相等B. 相邻C. 倒数D. 相反数答案：D解析：根据实数的性质，若a + b = 0，则a与b互为相反数。

2. 下列方程中，解为正数的是（）A. x + 1 = 0B. x - 1 = 0C. x^2 - 1 = 0D. x^2 + 1 = 0答案：C解析：解方程x^2 - 1 = 0，得到x = ±1，其中正数解为1。

3. 下列图形中，既是轴对称图形又是中心对称图形的是（）A. 等腰三角形B. 等边三角形C. 矩形D. 圆答案：D解析：矩形和圆既是轴对称图形又是中心对称图形。

4. 若a，b，c成等差数列，则（）A. a + b + c = 0B. a^2 + b^2 + c^2 = 3abcC. a^2 + b^2 + c^2 = 2ab + 2bc + 2acD. a^2 + b^2 + c^2 = (a + b + c)^2答案：C解析：由等差数列的性质可知，a + b + c = 3a，代入C选项得到a^2 + b^2 + c^2 = 2ab + 2bc + 2ac。

5. 若一个数的平方等于它本身，则这个数是（）A. 0B. 1C. -1D. 0或1答案：D解析：0的平方等于0，1的平方等于1，-1的平方等于1，因此这个数是0或1。

二、填空题（每题5分，共20分）6. 若x^2 - 4x + 3 = 0，则x的值为______。

答案：x = 1或x = 3解析：将方程因式分解得到(x - 1)(x - 3) = 0，解得x = 1或x = 3。

7. 若a，b，c成等比数列，则b^2 =______。

答案：b^2 = ac解析：由等比数列的性质可知，b^2 = ac。

8. 若a，b，c成等差数列，则a^2 + b^2 + c^2 =______。

答案：a^2 + b^2 + c^2 = (a + b + c)^2解析：由等差数列的性质可知，a^2 + b^2 + c^2 = (a + b + c)^2。

初中数学试卷桑水出品初二数学周清卷一次函数 3.29 （满分60分）一、选择（每题3分共27分）1.变量x,y有如下关系：①x+y=10②y=x5-③y=|x-3④y2=8x.其中y是x的函数的是A.①②②③④B. ①②③C. ①②D. ①2.下列各曲线中不能表示y是x的函数是（）．A．B．C．D．3.已知一次函数2y x a=+与y x b=-+的图象都经过A（2-，0），且与y轴分别交于B、C两点，则△ABC的面积为（）．A．4 B．5 C．6 D．74.已知正比例函数y=(k+5)x,且y随x的增大而减小，则k的取值范围是( )A.k＞5B.k＜5C.k＞-5D.k＜-55.在平面直角坐标系xoy中，点M(a,1)在一次函数y=-x+3的图象上，则点N(2a-1,a)所在的象限是( )A.一象限 B. 二象限 C. 四象限 D.不能确定6.如果通过平移直线3xy=得到53xy+=的图象，那么直线3xy=必须（）．A．向上平移5个单位B．向下平移5个单位C．向上平移53个单位D．向下平移53个单位7.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小，则函数y=kx-k的图象大致是0 9 16 30 t /分钟 s /km 40 128.若方程x-2=0的解也是直线y=(2k-1)x+10与x 轴的交点的横坐标，则k 的值为( )A.2B.0C.-2D. ±29.已知直线y 1=2x 与直线y 2= -2x+4相交于点A.有以下结论：①点A 的坐标为A(1,2);②当x=1时，两个函数值相等；③当x ＜1时，y 1＜y 2④直线y 1=2x 与直线y 2=2x-4在平面直角坐标系中的位置关系是平行.其中正确的是( )A. ①③④B. ②③C. ①②③④D. ①②③二、填空题（每题3分，共,18分）。

10.已知1(2)3n y m x -=-+是关于x 的一次函数，则m ，n ．11.直线23y x =-与x 轴的交点坐标是__________，与y 轴的交点坐标是__________．12.直线y=﹣2x+m 与直线y=2x ﹣1的交点在第四象限，则m 的取值范围是__________13．已知不等式-x+5>3x-3的解集是x<2，则直线y=-x+5与y=3x-3•的交点坐标是_________．14．当自变量x 的值满足____________时，直线y=-x+2上的点在x 轴下方．15．汽车行驶前，油箱中有油55升，已知每百千米汽车耗油10升，油箱中的余油量Q （升）与它行驶的距离s （百千米）之间的函数关系式为___ ________；为了保证行车安全，油箱中至少存油5升，则汽车最多可行驶____________千米．三、解答题（共15分。

检测内容：17.1－17.2得分________ 卷后分________ 评价________一、选择题(每小题4分,共32分)1．下列对函数的认识正确的是( D )A．若y是x的函数,那么x也是y的函数B．两个变量之间的函数关系一定能用数学式子表达C．若y是x的函数,则当y取一个值时,一定有唯一的x值与它对应D．一个人的身高也可以看作他年龄的函数2．(2018·娄底)函数y＝x－2x－3中自变量x的取值范围是( C )A．x＞2 B．x≥2C．x≥2且x≠3 D．x≠33．(2018·东营)在平面直角坐标系中,若点P(m－2,m＋1)在第二象限,则m的取值范围是( C )A．m＜－1 B．m＞2C．－1＜m＜2 D．m＞－14．在平面直角坐标系中,点P(－2,3)关于x轴的对称点是( A )A．(－2,－3) B．(2,－3)C．(－3,－2) D．(3,－2)5．下列各点中,不在函数y＝3x＋2的图象上的是( D )A．(0,2) B．(1,5)C．(－1,－1) D．(－2,－3)6．为了建设社会主义新农村,某市积极推进“行政村通畅工程”．张村和王村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,随后施工队加快了施工进度,按时完成了两村之间道路的改造．下面能反映该工程尚未改造道路里程y(千米)与时间x(天)的函数关系的大致图象是( D )7．(2018·齐齐哈尔)如图是自动测温仪记录的图象,它反映了齐齐哈尔市的春季某天气温T如何随时间t的变化而变化,下列从图象中得到的信息正确的是( D )A．0点时气温达到最低B．最低气温是零下4℃C．0点到14点之间气温持续上升D．最高气温是8℃8．如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,……顶点依次用A1,A2,A3,A4,……表示,则顶点A55的坐标为( C )A．(13,13) B．(－13,－13)C．(14,14) D．(－14,－14)二、填空题(每小题4分,共24分)9．点P(－5,2)关于y轴对称的点Q的坐标为__(5,2)__．10．我国是一个严重缺水的国家,珍惜水资源,杜绝水浪费,是我们每个公民应尽的责任．据测试,拧不紧的水龙头每秒钟滴下2滴水,每滴水约0.05毫升,小媛同学在洗手时,没有把水龙头拧紧便离开,当小媛离开x小时后,水龙头滴水y毫升,试写出y关于x的函数关系式：__y＝360x__,其中常量是__360__,变量是__x,y__．11．若点A在x轴上,距离原点3个单位,则点A的坐标为__(3,0)或(－3,0)__．12．若点P(2,2)在函数y＝ax2－3x的图象上,则a＝__2__．此时,当x＝1时,y＝__－1__；当x＝－1时,y＝__5__．13．如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别是A(－2,1)和B(－2,－3),那么第一架轰炸机的平面坐标是C__(2,－1)__．,第13题图) ,第14题图) 14．某人沿直路行走,设此人离出发地的距离s(千米)与行走时间t(分)的函数关系如图,则此人在这段时间内最快的行走速度是__8__千米/时．三、解答题(共44分)15．(6分) 已知函数y＝－x2＋2,判断点A(－1,1)和点B(2,1)是否在该函数图象上．点A(－1,1)在该函数图象上；点B(2,1)不在该函数图象上16．(8分)长方形的周长为20 cm,它的长为a cm,宽为b cm.(1)上述量哪些是常量？哪些是变量？(2)写出变量a与b之间的关系式；(3)试求当宽b的值分别为2,3.5时,相应的长a的值是多少？(4)当宽为多少时,长为6 cm?(1)20是常量,a,b是变量(2)a＝10－b(3)当b＝2时,a＝8；当b＝3.5时,a＝6.5(4)4 cm17．(10分)如图,在Rt△ABC中,∠C＝90°,AC＝6,BC＝8,点P在BC上运动,点P不与点B,C重合,设PC＝x,若用y表示△APB的面积,求y与x的函数关系式,并求自变量x的取值范围．y ＝24－3x (0＜x ＜8)18．(10分)小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,如图是她本次去舅舅家所用的时间与路程的关系示意图．根据图中提供的信息回答下列问题：(1)小红家到舅舅家的路程是__1500__米,小红在商店停留了__4__分钟；(2)本次去舅舅家,小红一共行驶了多少米？一共用了多少分钟？小红一共行驶了2700米,一共用了14分钟19．(10分)如图,在平面直角坐标系中,已知长方形OABC 的两个顶点的坐标分别为A (3,0),B (3,2),对角线AC 所在的直线为l .(1)求线段AC 的长．(2)在y 轴上是否存在使△ACP 为等腰三角形的点P ？若存在,请直接写出点P 的坐标；若不存在,请说明理由．解：(1)由题意可知,点C 的坐标为(0,2),AC ＝OC 2＋OA 2＝22＋32＝13 (2)存在,共有四个,分别为P 1(0,－2),P 2(0,2－13),P 3(0,13＋2),P 4(0,－54)。

特殊平行四边形与梯形一、选择题（每小题4分，共40分）1．下列说法中，不正确的是（）．（A）有三个角是直角的四边形是矩形;（B）对角线相等的四边形是矩形（C）对角线互相垂直的矩形是正方形;（D）对角线互相垂直的平行四边形是菱形2．已知一个四边形的对角线互相垂直，•那么顺次连接这个四边形的四边中点所得的四边形是（）．（A）矩形（B）菱形（C）等腰梯形（D）正方形3．用两个全等的直角三角形拼下列图形：①矩形；②菱形；③正方形；④平行四边形；⑤等腰三角形；⑥等腰梯形．其中一定能拼成的图形是（）．（A）①②③（B）①④⑤（C）①②⑤（D）②⑤⑥4．如图1，在梯形ABCD中，AD∥BC，AB=DC，∠C=60°，BD 平分∠ABC．如果这个梯形的周长为30，则AB的长为（）．（A）4 （B）5 （C）6 （D）7(1) (2) (3)5．如图2，矩形ABCD沿AE折叠，使点D落在BC边上的F点处，如果∠BAF=60°，那么∠DAE等于（）．（A）15°（B）30°（C）45°（D）60°6．如图3，在菱形ABCD中，∠ADC=120°，则BD：AC等于（）．（A 2 （B 3 （C）1：2 （D 1 7．如图4，四边形ABCD是正方形，延长BC至点E，使CE=CA，连结AE交CD•于点F，•则∠AFC的度数是（）．（A）150°（B）125°（C）135°（D）112．5°8．如图5，在等腰梯形ABCD中，AD∥BC，AC，BD相交于点O．•有下列四个结论：•①AC=BD；②梯形ABCD是轴对称图形；③∠ADB=∠DAC；④△AOD≌△ABO．其中正确的是（）．（A）①③④（B）①②④（C）①②③（D）②③④(4) (5) 9．一张矩形纸片按如图甲或乙所示对折，然后沿着图丙中的虚线剪下，得到①，•②两部分，将①展开后得到的平面图形是（）．（A）三角形（B）矩形（C）菱形（D）梯形10．小许拿了一张正方形的纸片如图甲，沿虚线对折一次得图乙．•再对折一次得图丙．然后用剪刀沿图丙中的虚线（虚线与底边平行）剪去一个角．打开后的形状是（•）．二、填空题（每小题4分，共40分）11．既是轴对称图形，又是中心对称图形的四边形是_________．12．把“直角三角形、等腰三角形、•等腰直角三角形”填入下列相应的空格上：（1）正方形可以由两个能够完全重合的_________拼合而成；（2）菱形可以由两个能够完全重合的_________拼合而成；（3）矩形可以由两个能够完全重合的________拼合而成．13．在平行四边形ABCD中，若添加一个条件________，则四边形ABCD是矩形；若添加一个条件_______，则四边形ABCD是菱形．14．已知正方形的面积为4，则正方形的边长为________，对角线长为________．15．已知矩形的对角线长为4cm，一条边长为，则面积为________．16．菱形的两条对角线分别是6cm，8cm，则菱形的边长为_____，面积为______．17．如图6，在四边形ABCD是正方形，△CDE是等边三角形，则∠AED=______，∠AEB=______．(6) (7) (8)18．如图7，在等腰梯形ABCD中，AD∥BC，•AD=•6cm，•BC=•8cm，•∠B=•60•°，•则AB=_______cm．19．现有一张长53cm，宽28cm的矩形纸片，要从中剪出长15cm，宽12cm的矩形小纸片，则最多能剪出______张．20．如图8，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，E•为垂足，连结DF，则∠CDF的度数=________．三、解答题（20分）21．（6分）如图，在菱形ABCD中，∠A与∠B的度数比为1：2，周长是48cm．求：（1）两条对角线的长度；（2）菱形的面积．22．（6分）已知：如图，在正方形ABCD中，AE⊥BF，垂足为P，AE与CD交于点E，•BF•与AD交于点F，求证：AE=BF．23、（8分）把一个等腰直角三角形ABC沿斜边上的高线CD(裁剪线)剪一刀，从这个三角形中裁下一部分，与剩下部分能拼成一个平行四边形A'BCD(如图1)．以下探究过程中有画图要求的，工具不限，不必写画法和证明．探究一：(1)想一想——判断四边形A'BCD是平行四边形的依据是__________；(2)做一做——按上述的裁剪方法，请你拼一个与图1位置或形状不同的平行四边形，并在图2中画出示意图．探究二：在等腰直角三角形ABC中，请你找出其它的剪裁线，把分割成的两部分拼出不同类型的特殊四边形．(1)试一试——你能拼得所有不同类型的特殊四边形有_________，它们的裁剪线分别是_________．(2)画一画——请在图3中画出一个你拼得的特殊四边形示意图。