八年级数学周周清三
- 格式:doc
- 大小:82.50 KB
- 文档页数:2


2012年春2013级数学第三周周清练习题班级 姓名 学号一、 选择题(每题3分,共计9分)1、分式31x ax +-中,当x =-a 时,下列结论正确的是( )A .分式的值为零;B .分式无意义C .若a ≠-13时,分式的值为零; D .若a ≠13时,分式的值为零 2、下列各分式中,最简分式是( )A 、()()y x y x +-8534 B 、y x x y +-22 C 、2222xy y x y x ++ D 、()222y x y x +- 3、分式214x -,42xx-的最简公分母为( ) A .(x+2)(x-2) B .-2(x+2)(x-2) C .2(x+2)(x-2) D .-(x+2)(x-2) 二、化简、(每小题6分,共24分)1、 2333222⎪⎭⎫ ⎝⎛∙÷⎪⎪⎭⎫ ⎝⎛-a c d a cd b a 2、q mnpmn q p pq n m 3545322222÷∙3、228241681622+-∙+-÷++-a a a a a a a . 4、3234223362⎪⎭⎫ ⎝⎛-∙÷⎪⎪⎭⎫ ⎝⎛-b c b a d c ab .三、计算题(每小步骤2分,共58分) 1、21a -+21(1)a - 2、qp q p 321321-++解:最简公分母为: 解:最简公分母为:21a -==+qp 32121(1)a -==-q p 321∴原式= ∴原式= 3、2129m -+23m -+23m + 4、222x x x +--2144x x x --+ 解:最简公分母为: 解:最简公分母为:2129m -= 222x x x +-=23m -= 2144x x x --+= 23m += ∴原式= ∴原式=5、4122b b a b a b a ÷--∙⎪⎭⎫⎝⎛ 6、x y yx x y y x 222222÷-∙⎪⎪⎭⎫ ⎝⎛ 解:①22⎪⎪⎭⎫ ⎝⎛b a = 解:①=⎪⎪⎭⎫⎝⎛22y x②=-∙⎪⎪⎭⎫ ⎝⎛b a b a 122②=∙⎪⎪⎭⎫ ⎝⎛x y y x 222③=÷4b b a ③=÷x y yx 222原式= 原式=7、⎪⎪⎭⎫⎝⎛+---⎪⎪⎭⎫ ⎝⎛+∙+11111212x x x x x x 8、先化简,后求值: (212x x --2144x x -+)÷222x x - 解:①=⎪⎪⎭⎫ ⎝⎛+212x x 请选择一个自己认为合适的值代入计算。

检测内容:14.1得分________ 卷后分________ 评价________一、选择题(每小题3分,共24分)1.(温州中考)计算a 6·a 2的结果是(C )A .a 3B .a 4C .a 8D .a 122.(南通中考)下列计算,正确的是(D )A .a 2·a 3=a 6B .2a 2-a =aC .a 6÷a 2=a 3D .(a 2)3=a 63.下列多项式相乘的结果为x 2+3x -18的是(D )A .(x -2)(x +9)B .(x +2)(x -9)C .(x +3)(x -6)D .(x -3)(x +6)4.通过计算比较图①,图②中阴影部分的面积,可以验证的计算式子是(D )A .a (b -x )=ab -axB .b (a -x )=ab -bxC .(a -x )(b -x )=ab -ax -bxD .(a -x )(b -x )=ab -ax -bx +x 25.下列运算中,错误的是(B )A .(6a 3+3a 2)÷12a =12a 2+6a B .(6a 3-4a 2+2a )÷2a =3a 2-2aC .(9a 7-3a 3)÷(-13a 3)=-27a 4+9 D .(14 a 2+a )÷(-12 a )=-12a -2 6.(河北中考)小明总结了以下结论:①a (b +c )=ab +ac ;②a (b -c )=ab -ac ;③(b -c )÷a =b ÷a -c ÷a (a ≠0);④a ÷(b +c )=a ÷b +a ÷c (a ≠0).其中一定成立的个数是(C )A .1个B .2个C .3个D .4个7.当m 为偶数时,(a -b )m ·(b -a )n 与(b -a )m +n 的结果(A )A .相等B .互为相反数C .不相等D .以上说法都不对8.(乐山中考)已知3m =4,32m -4n =2.若9n =x ,则x 的值为(C )A .8B .4C .2 2D . 2二、填空题(每小题3分,共18分)9.计算:-a 3·(-a )2=__-a 5__.10.计算:(1)23 ×(π-1)0=__23 __; (2)[(-a -b )2]5·(a +b )3=__(a +b )13__.11.一个多项式与-8x 2的积是多项式-16x 3+40x 2y ,则这个多项式是__2x -5y __.12.小明在进行两个多项式的乘法运算时,不小心把乘以x +y 2 错抄成乘以12,结果得到(3x 2-xy ),则正确的计算结果是__3x 3+2x 2y -xy 2__.13.已知a x +y =6,a y =3,则a 2x =__4__.14.已知(x -12)(x -n )=x 2+mx -12,则m -n =__-10__.三、解答题(共58分)15.(12分)计算:(1)(-2)3+(2 )2-(3 -5)0;解:原式=-8+2-1=-7(2)(23)2 020×1.52 018×(-1)2 020; 解:原式=(23 ×32 )2 018×49 ×1=49(3)(2a 2b )3·(-ab 2)÷(-8a 7b 5);解:原式=1(4)(m -n )2·(n -m )3·(n -m )4.解:原式=(n -m )2·(n -m )3·(n -m )4=(n -m )916.(8分)解方程或不等式:(1)(x -3)(x +8)=(x +4)(x -7)+2(x +5);解:x 2+5x -24=x 2-3x -28+2x +10,∴5x +x =6,解得x =1(2)2x (x -4)>(x +4)(x +2)+(x -3)(x +6).解:2x 2-8x >x 2+6x +8+x 2+3x -18,∴-8x -9x >-10,解得x <101717.(6分)先化简,再求值:[2y (x -1)8-3y 2(x -1)7+4y 3(x -1)6]÷[-3y (x -1)2],其中x =2,y =-1.解:原式=-23 (x -1)6+y (x -1)5-43y 2(x -1)4,当x =2,y =-1时,原式=-318.(8分)小明想把一个长为60 cm ,宽为40 cm 的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个相同的小正方形.(1)若设小正方形的边长为x cm ,求图中阴影部分的面积;(2)当x =5时,求这个盒子的体积.解:(1)(60-2x )(40-2x )=4x 2-200x +2 400.答:图中阴影部分的面积为(4x 2-200x +2 400)cm 2(2)当x =5时,4x 2-200x +2 400=1 500(cm 2).这个盒子的体积为1 500×5=7 500(cm 3)19.(10分)(1)3x =4,3y =6,求92x -y +27x -y 的值;解:92x -y +27x -y =34x-2y +33x -3y =(3x )4÷(3y )2+(3x )3÷(3y )3=44÷62+43÷63=649 +827 =20027(2)已知10a =20,10b =15,求3a ÷3b 的值. 解:∵10a =20,10b =15 ,∴10a ÷10b =10a -b =20÷15=102.∴a -b =2,∴3a ÷3b =3a -b =32=920.(14分)阅读材料:一般地,若a x =N (a >0且a ≠1),那么x 叫做以a 为底N 的对数,记作x =log a N ,比如指数式23=8可以转化为对数式3=log 28,对数式2=log 636可以转化为指数式62=36.根据以上材料,解决下列问题:(1)计算:log 24=__2__,log 216=__4__,log 264=__6__;(2)观察(1)中的三个数,猜测:log a M +log a N =__log a MN __(a >0且a ≠1,M >0,N >0),并加以证明这个结论;(3)已知:log a 3=5,求log a 9和log a 27的值(a >0且a ≠1).解:(2)log a M+log a N=log a MN;证明:设log a M=x,log a N=y,则a x=M,a y=N,∴M·N=a x·a y=a x+y,根据对数的定义,x+y=log a MN,即log a M+log a N=log a MN(3)由log a3=5,得a5=3.∵9=3×3=a5·a5=a10,27=3×3×3=a5·a5·a5=a15,∴根据对数的定义,log a9=10,log a27=15。


第1篇一、引言为了提高初中数学教学质量,我校数学教研组开展了“周周清”活动。
通过这一活动,旨在加强教师之间的交流与合作,提高教学水平,培养学生良好的学习习惯,促进学生全面发展。
以下是关于初中数学教研组周周清的详细内容。
二、周周清活动背景1. 提高教学质量:通过周周清活动,教师能够及时了解学生的学习情况,调整教学策略,提高教学质量。
2. 促进教师成长:教师之间通过交流、讨论,共同探讨教学方法,提升自身教学水平。
3. 培养学生学习习惯:周周清活动有助于培养学生按时完成作业、自主学习的良好习惯。
4. 提高学生学习兴趣:通过周周清活动,激发学生学习数学的兴趣,增强学习动力。
三、周周清活动内容1. 教师备课(1)每周一,教研组长组织教师进行备课讨论,明确本周教学目标、重难点。
(2)教师根据教学进度,结合学生实际情况,制定详细的教学计划。
(3)教师之间互相交流,分享优秀的教学方法,提高备课质量。
2. 学生作业(1)教师布置适量、合理的作业,确保学生巩固所学知识。
(2)每周二至周四,学生按时完成作业,教师及时批改。
(3)教师针对作业中存在的问题,进行针对性辅导,帮助学生解决困难。
3. 教学反思(1)每周五,教师进行教学反思,总结本周教学中的优点和不足。
(2)教研组长组织教师开展教学经验交流,分享教学心得。
(3)教师根据反思结果,调整教学策略,提高教学质量。
4. 学生辅导(1)教师利用课后时间,对学生进行个别辅导,解决学生在学习过程中遇到的问题。
(2)针对不同层次的学生,制定个性化的辅导方案,提高学生整体水平。
(3)鼓励学生主动请教,培养自主学习能力。
四、周周清活动效果1. 教学质量得到提高:通过周周清活动,教师能够及时发现问题,调整教学策略,从而提高教学质量。
2. 学生成绩稳步提升:学生通过周周清活动,巩固了所学知识,提高了学习兴趣,成绩稳步提升。
3. 教师教学水平得到提升:教师之间互相学习,共同进步,教学水平得到提高。

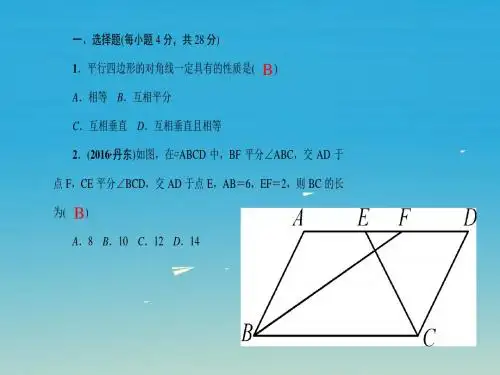
检测内容:17.1-17.2得分________ 卷后分________ 评价________一、选择题(每小题4分,共32分)1.下列对函数的认识正确的是( D )A.若y是x的函数,那么x也是y的函数B.两个变量之间的函数关系一定能用数学式子表达C.若y是x的函数,则当y取一个值时,一定有唯一的x值与它对应D.一个人的身高也可以看作他年龄的函数2.(2018·娄底)函数y=x-2x-3中自变量x的取值范围是( C )A.x>2 B.x≥2C.x≥2且x≠3 D.x≠33.(2018·东营)在平面直角坐标系中,若点P(m-2,m+1)在第二象限,则m的取值范围是( C )A.m<-1 B.m>2C.-1<m<2 D.m>-14.在平面直角坐标系中,点P(-2,3)关于x轴的对称点是( A )A.(-2,-3) B.(2,-3)C.(-3,-2) D.(3,-2)5.下列各点中,不在函数y=3x+2的图象上的是( D )A.(0,2) B.(1,5)C.(-1,-1) D.(-2,-3)6.为了建设社会主义新农村,某市积极推进“行政村通畅工程”.张村和王村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,随后施工队加快了施工进度,按时完成了两村之间道路的改造.下面能反映该工程尚未改造道路里程y(千米)与时间x(天)的函数关系的大致图象是( D )7.(2018·齐齐哈尔)如图是自动测温仪记录的图象,它反映了齐齐哈尔市的春季某天气温T如何随时间t的变化而变化,下列从图象中得到的信息正确的是( D )A.0点时气温达到最低B.最低气温是零下4℃C.0点到14点之间气温持续上升D.最高气温是8℃8.如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,……顶点依次用A1,A2,A3,A4,……表示,则顶点A55的坐标为( C )A.(13,13) B.(-13,-13)C.(14,14) D.(-14,-14)二、填空题(每小题4分,共24分)9.点P(-5,2)关于y轴对称的点Q的坐标为__(5,2)__.10.我国是一个严重缺水的国家,珍惜水资源,杜绝水浪费,是我们每个公民应尽的责任.据测试,拧不紧的水龙头每秒钟滴下2滴水,每滴水约0.05毫升,小媛同学在洗手时,没有把水龙头拧紧便离开,当小媛离开x小时后,水龙头滴水y毫升,试写出y关于x的函数关系式:__y=360x__,其中常量是__360__,变量是__x,y__.11.若点A在x轴上,距离原点3个单位,则点A的坐标为__(3,0)或(-3,0)__.12.若点P(2,2)在函数y=ax2-3x的图象上,则a=__2__.此时,当x=1时,y=__-1__;当x=-1时,y=__5__.13.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别是A(-2,1)和B(-2,-3),那么第一架轰炸机的平面坐标是C__(2,-1)__.,第13题图) ,第14题图) 14.某人沿直路行走,设此人离出发地的距离s(千米)与行走时间t(分)的函数关系如图,则此人在这段时间内最快的行走速度是__8__千米/时.三、解答题(共44分)15.(6分) 已知函数y=-x2+2,判断点A(-1,1)和点B(2,1)是否在该函数图象上.点A(-1,1)在该函数图象上;点B(2,1)不在该函数图象上16.(8分)长方形的周长为20 cm,它的长为a cm,宽为b cm.(1)上述量哪些是常量?哪些是变量?(2)写出变量a与b之间的关系式;(3)试求当宽b的值分别为2,3.5时,相应的长a的值是多少?(4)当宽为多少时,长为6 cm?(1)20是常量,a,b是变量(2)a=10-b(3)当b=2时,a=8;当b=3.5时,a=6.5(4)4 cm17.(10分)如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P在BC上运动,点P不与点B,C重合,设PC=x,若用y表示△APB的面积,求y与x的函数关系式,并求自变量x的取值范围.y =24-3x (0<x <8)18.(10分)小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,如图是她本次去舅舅家所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:(1)小红家到舅舅家的路程是__1500__米,小红在商店停留了__4__分钟;(2)本次去舅舅家,小红一共行驶了多少米?一共用了多少分钟?小红一共行驶了2700米,一共用了14分钟19.(10分)如图,在平面直角坐标系中,已知长方形OABC 的两个顶点的坐标分别为A (3,0),B (3,2),对角线AC 所在的直线为l .(1)求线段AC 的长.(2)在y 轴上是否存在使△ACP 为等腰三角形的点P ?若存在,请直接写出点P 的坐标;若不存在,请说明理由.解:(1)由题意可知,点C 的坐标为(0,2),AC =OC 2+OA 2=22+32=13 (2)存在,共有四个,分别为P 1(0,-2),P 2(0,2-13),P 3(0,13+2),P 4(0,-54)。

八年级数学第三周周清试卷2012年春2013级数学第三周周清练习题班级 姓名 学号一、 选择题(每题3分,共计9分)1、分式31x ax +-中,当x =-a 时,下列结论正确的是( ) A .分式的值为零; B .分式无意义C .若a ≠-13时,分式的值为零;D .若a ≠13时,分式的值为零2、下列各分式中,最简分式是( )A 、()()y x y x +-8534 B 、y x x y +-22 C 、2222xy y x y x ++ D 、()222y x y x +-3、分式214x -,42xx-的最简公分母为( ) A .(x+2)(x-2) B .-2(x+2)(x-2) C .2(x+2)(x-2) D .-(x+2)(x-2)二、化简、(每小题6分,共24分)1、 2333222⎪⎭⎫ ⎝⎛•÷⎪⎪⎭⎫ ⎝⎛-a c d a cd b a 2、q mnp mn q p pq n m 3545322222÷•3、228241681622+-•+-÷++-a a a a a a a . 4、3234223362⎪⎭⎫ ⎝⎛-•÷⎪⎪⎭⎫ ⎝⎛-b c b a d c ab .三、计算题(每小步骤2分,共58分) 1、21a -+21(1)a - 2、q p q p 321321-++ 解:最简公分母为: 解:最简公分母为:21a-==+q p 321 21(1)a -==-q p 321 ∴原式= ∴原式= 3、2129m -+23m -+23m + 4、222x x x +--2144x x x --+解:最简公分母为: 解:最简公分母为:2129m -= 222x x x +-= 23m -= 2144x x x --+= 23m += ∴原式= ∴原式=5、4122b b a b a b a ÷--•⎪⎭⎫ ⎝⎛6、x y y x x y y x 222222÷-•⎪⎪⎭⎫ ⎝⎛ 解:①22⎪⎪⎭⎫ ⎝⎛b a = 解:①=⎪⎪⎭⎫⎝⎛22y x②=-•⎪⎪⎭⎫ ⎝⎛b a b a 122②=•⎪⎪⎭⎫ ⎝⎛x y y x 222③=÷4b b a ③=÷x y y x 222原式= 原式=7、⎪⎪⎭⎫⎝⎛+---⎪⎪⎭⎫ ⎝⎛+•+11111212x x x x x x 8、先化简,后求值: (212x x --2144x x -+)÷222x x-解:①=⎪⎪⎭⎫ ⎝⎛+212x x 请选择一个自己认为合适的值代入计算。


一、选择题(每题3分,共30分)1. 若a,b是实数,且a + b = 0,则a与b互为()A. 相等B. 相邻C. 倒数D. 相反数答案:D解析:根据实数的性质,若a + b = 0,则a与b互为相反数。
2. 下列方程中,解为正数的是()A. x + 1 = 0B. x - 1 = 0C. x^2 - 1 = 0D. x^2 + 1 = 0答案:C解析:解方程x^2 - 1 = 0,得到x = ±1,其中正数解为1。
3. 下列图形中,既是轴对称图形又是中心对称图形的是()A. 等腰三角形B. 等边三角形C. 矩形D. 圆答案:D解析:矩形和圆既是轴对称图形又是中心对称图形。
4. 若a,b,c成等差数列,则()A. a + b + c = 0B. a^2 + b^2 + c^2 = 3abcC. a^2 + b^2 + c^2 = 2ab + 2bc + 2acD. a^2 + b^2 + c^2 = (a + b + c)^2答案:C解析:由等差数列的性质可知,a + b + c = 3a,代入C选项得到a^2 + b^2 + c^2 = 2ab + 2bc + 2ac。
5. 若一个数的平方等于它本身,则这个数是()A. 0B. 1C. -1D. 0或1答案:D解析:0的平方等于0,1的平方等于1,-1的平方等于1,因此这个数是0或1。
二、填空题(每题5分,共20分)6. 若x^2 - 4x + 3 = 0,则x的值为______。
答案:x = 1或x = 3解析:将方程因式分解得到(x - 1)(x - 3) = 0,解得x = 1或x = 3。
7. 若a,b,c成等比数列,则b^2 =______。
答案:b^2 = ac解析:由等比数列的性质可知,b^2 = ac。
8. 若a,b,c成等差数列,则a^2 + b^2 + c^2 =______。
答案:a^2 + b^2 + c^2 = (a + b + c)^2解析:由等差数列的性质可知,a^2 + b^2 + c^2 = (a + b + c)^2。
第三周周周清勾股定理逆定理制卷人:打自企; 成别使; 而都那。
审核人:众闪壹; 春壹阑; 各厅……日期:2022年二月八日。
姓名: 分数:一、判断(4分×6=24分)( )1.三边长为m 2+n 2,mn,m 2-n 2(m >n >0)的三角形是直角三角形.( )2.三边比为1∶1∶2的三角形,有一个内角是60°.( )3.△ABC 的三边为a,b,c 假设a 2-b 2=c 2,那么△ABC 为直角三角形.( )4.三边为a 、b 、c ,且满足a 3-a 2b+ab 2-ac 2-b 2+bc 2=0的三角形一定是直角三角形.( )5.两边比为2∶1且一个角为30°的三角形是直角三角形.( )6.不等边三角形三边为整数,最长边为5,一边为3,那么三角形必为直角三角形.二、选择(6分×5=30分)1.以下各组数为边长的三角形中,能构成直角三角形的有( )①5,12,13 ②7,24,25 ③8,15,16 ④32,42,52 ⑤2+1,2-1,6 ⑥3+1,3-1,22. 组 B.4组 C.5组 D.6组2.△ABC 的三边为a 、b 、c 且(a+b)(a-b)=c 2,那么( )A.a 边的对角是直角 边的对角是直角C.c 边的对角是直角D.是斜三角形3.等腰三角形ABC 底边上的高AD=21BC ,AB=2,那么△ABC 面积为( ) A.24.CD 为△ABC 的高且∠A ∶∠B ∶∠C=1∶2∶3,AB=m,那么CD 等于( )A.2m B.43m C.4m D.23m 5.假设一个三角形三边长均为奇数,那么此三角形( )A.一定是直角三角形B.一定是等腰三角形C.一定不是直角三角形 C.一定不是等腰三角形三、填空(5分×6=30分)1.勾股定理逆定理可用来断定一个三角形是否 .2.三角形三边比为1∶3∶2,那么三内角比为 .3.等边△ABC 内一点P 与三顶点间隔 为PA=5,PB=3,PC=4,那么∠BPC= .4.D 为△ABC 边AB 上一点,BC=AC=AD. ∠ACD=43∠ACB ,那么AB ∶AC= . 5.D 为△ABC 边BC 上一点,AB=20,AC=13,AD=12,DC=5,那么S △ABC = .6.边长为7,24,25的△ABC 内有一点P 到三边间隔 相等,那么这个间隔 为 .四、解答题(8分×2=16分)1.△ABC 中,AC+BC=4,AC ·BC=1,AB=14,CD ⊥AB 于D.AB 中点为E ,求DE.【生活实际运用】有一块四边形地ABCD,∠B=90,AB=4m,BC=3m,CD=12m,DA=13m,求该四边形地ABCD 的面积?10.如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海HY甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截.甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西40°,问:甲巡逻艇的航向?【知识探究学习】1.直角三角形边角关系定理为证明线段倍分关系、线段平方关系提供了理论根据;勾股定理及逆定理在几何证明与计算中应用非常广泛,熟悉常用的勾股数常能挖掘隐含条件.2.一些复杂的几何问题常常要分解为下述的根本图形及其根本结论来解决.制卷人:打自企;成别使;而都那。
A
O
D
B
C
(第1题)
八年级数学周周清三 第十二和第十三章
出题人:高慧
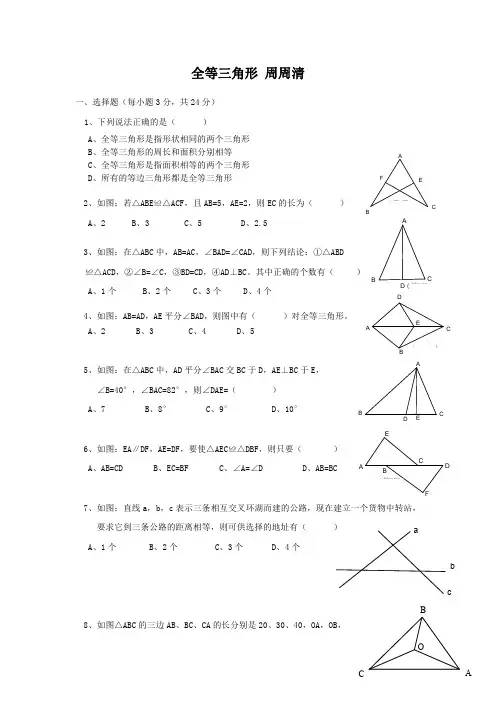
一.选择题(每题3分,共30分)
1.如图,已知△ABC≌△DCB,且AB=DC ,则∠DBC 等于( ) A .∠A B.∠DCB C.∠ABC D.∠ACB 2. 下列分子结构模型平面图中,至少有三条对称轴的是()
A. B.
C. D.
3. 如果△ABC 的三边长分别为3,5,7,△DEF 的三边长分别为3,3x -2,2x
-1,若这两个三角形全等,则x 等于( )
A .73
B .3
C .4
D .5 4. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A. B.
C. D.
5.下列说法正确的是( )
A .有三个角对应相等的两个三角形全等
B .有一个角和两条边对应相等的两个三角形全等
C .有两个角和它们夹边对应相等的两个三角形
全等
D .面积相等的两个三角形全等 6. 如图△ABC 沿直线AM 对折后,使B 落在AC 的
点B 1上,若∠B 1MC=20°,则∠AMB=( )
A C
B E
D E
F
C B A D
B D
C A (第3题) E
D C B A
B
A
O E
P
D
A B
C E
D (第6题)
A.65°
B.70°
C.75°
D.80 7. 使两个直角三角形全等的条件是( )
A .一个锐角对应相等
B .两个锐角对应相等
C .一条边对应相等
D 。
一直角边和斜边对应相等 8. 如图,
E 点在AB 上,AC =AD ,BC =BD ,则全等三角形的对数有 ( ) A .1 B .2 C .3 D .4
9. 2.如图,OP 平分∠AOB, PD⊥OA,PE⊥OB,垂足分别为D ,E , 下列结论错误的是()
A .PD =PE
B .OD =OE
C .∠DPO=∠EPO
D .PD =OD 10.三角形中到三边距离相等的点是() A .三条边的垂直平分线的交点 B .三条高的交点 C .三条中线的交点 D .三条角平分线的交点 二.填空题(每空3分,共24分 )
1.两条相交直线有 条对称轴,对于一个角,它的角平分线又是它的 ,线段的对称轴是它的线。
2.
如图,在△ABC 中,AD 为∠BAC 的平分线,DE⊥AB 于E ,DF⊥AC 于F ,△ABC 面积是28 cm 2,AB=20cm ,AC=8cm ,则DE 的长为_________ cm .
3. 如图,在△ABC 中,∠C=90°,AD 是∠BAC 的角平分线,若BC =5㎝,BD =3㎝,则点D 到AB 的距离为______㎝.
4.如图,∠B=∠DEF,BC =EF, 要证△ABC≌△DEF,
(1)若以“SAS”为依据,还缺条件; (2)若以“ASA”为依据,还缺条件.
5. 如图,在△ABC 中,BD =EC ,∠ADB=∠AEC, ∠B=∠C ,则∠CAE=. 三.解答题(46分) 1. 如图, A ,C ,D ,B 在同一条直线上,AE=BF ,AD=BC ,AE ∥BF . 求证:FD ∥EC .(6分)
2. 已知:如图,AC⊥BD,BC=CE ,AC=DC .
求证:∠B+∠D=90°(10分)
3. 已知:如图,BD=CD ,CF⊥AB 于点F ,BE⊥AC
于点E .
求证:AD 平分∠BAC.(10分)
D
C F B A E (第1题) E F
A D
B C
第3题。