求复合函数偏导数的链式法则解
- 格式:ppt
- 大小:599.01 KB
- 文档页数:26






复合函数求导(链式法则)(建议阅读原文)预备知识微分若有两个一元函数 f(x) 和 g(x),我们可以把 g 的函数值作为 f 的自变量,得到一个新的函数称为f(x) 和 g(x) 的复合函数,记为 f[g(x)].如果我们已知两个函数 f(x) 和 g(x) 的导函数 f'(x) 和 g'(x),那么我们可以通过以下公式求复合函数 f[g(x)] 的导数.\begin{align}&f[g(x)]' = f'[g(x)]g'(x)&(1)\\\end{align}对于多个函数的复合函数,我们也有类似的公式,例如\begin{align}&f[g(h(x))]' =f'[g(h(x))]g'[h(x)]h'(x)&(2)\\\end{align}例1 基本初等函数的复合函数求导我们已经知道基本初等函数的导数的导函数,下面对它们的一些常见的复合函数进行求导. \sin^2 x 可以看作幂函数 f(x) = x^2 和 g(x) =\sin x 的复合函数,已知 f'(x) = 2x, g'(x) = \cos x,代入式 1 得\begin{align}&(\sin^2 x)' = 2\sin x \cosx&(3)\\\end{align}几何理解为了方便表示,我们把 g 的函数值和 f 的自变量记为 u,把 f 的函数值记为 y.图 1:可以将 \sin^2 x 看做 f(u) = u^2 和 g(x) = \sin x 的复合函数我们可以用类似图 1 的图像来直观地理解复合函数.先画出y = f(u) 和 u = g(x) 的图像,并将 g(u) 的图像逆时针旋转90° 使得两图的 u 轴对齐.这样对于任何定义域中的自变量 x,我们只需要先在 g(x) 的图中画出 u 的位置,再对应到 f(u) 的图像中求出 y 的位置即可.现在我们要讨论的问题是,若已知两函数的导函数 f'(x) 和 g'(u)(假设它们在定义域内处处可导)如何求复合函数 f[g(x)] 的导数.对于给定的 x,我们先来看当 x 增加 \Delta x 时 y 的增量 \Delta y 的大小.我们可以使用与图 1 类似的方法画出图 2 ,然后只需要令 \Delta x \to 0,就可以根据定义求出复合函数的导数\begin{align}&f[g(x)]' =\frac{\mathrm{d}}{\mathrm{d}{x}} f[g(x)] =\lim_{\Delta x\to 0} \frac{\Delta y}{\Deltax}&(4)\\\end{align}图 2:用图 1 中的方法求出任意 \Delta x 对应的 \Delta y在这个过程中,我们在得到 \Delta y 之前先得到了 u 的增量 \Delta u.当 \Delta x 较小时有微分近似(式2 )\begin{align}&\Delta {u} \approx g'(x) \Delta{x}\qquad \Delta{y} \approx f'(u)\Delta{u}&(5)\\\end{align}当 \Delta x \to 0 时对应的微分关系(式 1 )为\begin{align}&\,\mathrm{d}{u} = g'(x) \,\mathrm{d}{x} \qquad \,\mathrm{d}{y} = f'(u)\,\mathrm{d}{u}&(6)\\\end{align}将上式中的左边代入右边得 \begin{align}&\,\mathrm{d}{y} = f'(u) g'(x) \,\mathrm{d}{x} = f'[g(x)]g'(x)\,\mathrm{d}{x}&(7)\\\end{align}而复合函数的微分是 \begin{align}&\,\mathrm{d}{y} =f[g(x)]' \,\mathrm{d}{x}&(8)\\\end{align}对比以上两式(微分和导数的关系)得\begin{align}&f[g(x)]' = f'[g(x)]g'(x)&(9)\\\end{align}这就是复合函数的求导公式.在上面的例子中\begin{align}&g(x) = \sin x \qquad g'(x) = \cos x\qquad f(u) = u^2 \qquad f'(u) = 2u\qquad&(10)\\\end{align}代入上式得\begin{align}&\frac{\mathrm{d}}{\mathrm{d}{x}} \sin^2 x = 2\sin x \cos x&(11)\\\end{align}复合函数的求导公式也叫链式法则,原因是我们可以把以上推导过程用导数的另外一种符号表示如下.\begin{align}&\,\mathrm{d}{y} =\frac{\mathrm{d}{y}}{\mathrm{d}{u}} \,\mathrm{d}{u} = \frac{\mathrm{d}{y}}{\mathrm{d}{u}}\frac{\mathrm{d}{u}}{\mathrm{d}{x}}\,\mathrm{d}{x}&(12)\\\end{align}得 \begin{align}&\frac{\mathrm{d}{y}}{\mathrm{d}{x}} = \frac{\mathrm{d}{y}}{\mathrm{d}{u}}\frac{\mathrm{d}{u}}{\mathrm{d}{x}}&(13)\\\end{align}这种书写方式让人不禁想把 \mathrm{d}{y}/\mathrm{d}{x} 看做是 \,\mathrm{d}{y} 和 \,\mathrm{d}{x} 相除,这样的符号分割是错误的,尤其是在以后学习高阶导数和偏导数时.多重复合函数要对多重复合函数如 f[g(h(x))] 求导,可以先对 g[h(x)] 求导得 g'[h(x)]h'(x) 再得到\begin{align}&f[g(h(x))]' =f'[g(h(x))]g'[h(x)]h'(x)&(14)\\\end{align}令 v = h(x),用微分符号可以表示为\begin{align}&\frac{\mathrm{d}{y}}{\mathrm{d}{x}} =\frac{\mathrm{d}{y}}{\mathrm{d}{u}}\frac{\mathrm{d}{u}}{\mathrm{d}{v}}\frac{\mathrm{d}{v}}{\mathrm{d}{x}}&(15)\\\end{align}任意多重的复合函数求导同理可得.例2 对函数求导\begin{align}&\frac{1}{\sqrt{x^2+a^2}}&(16)\\\end{alig n}首先令 f(x) = 1/\sqrt{x} 再令 g(x) = x^2+a^2,上式等于 f[g(x)].由基本初等函数的导数, \begin{align}&f'(x) = -\frac{1}{2\sqrt{x^3}} \qquad g'(x) =2x&(17)\\\end{align}代入式 9 ,得\begin{align}&\frac{\mathrm{d}}{\mathrm{d}{x}}\frac{1}{\sqrt{x^2+a^2}} = f'[g(x)] g'(x) = -\frac{x}{\sqrt{(x^2+a^2)^3}}&(18)\\\end{align}一种较灵活的情况是,当三个变量只有一个自由度1时,任何一个变量都可以看做任何另外两个变量的函数2,这时可以根据需要灵活运用链式法则,如例 3 .例3 加速运动公式假设质点做一维运动,位移,速度和加速度分别记为 x(t), v(t) = \mathrm{d}{x}/\mathrm{d}{t},a(t) = \mathrm{d}{v}/\mathrm{d}{t},但若把速度 v 看做复合函数 v[x(t)],根据链式法则有\begin{align}&a = \frac{\mathrm{d}{v}}{\mathrm{d}{t}} = \frac{\mathrm{d}{v}}{\mathrm{d}{x}}\frac{\mathrm{d}{x}}{\mathrm{d}{t}} =\frac{\mathrm{d}{v}}{\mathrm{d}{x}} v&(19)\\\end{align}写成微分表达式,有 a \,\mathrm{d}{x} = v\,\mathrm{d}{v}.注意到 \,\mathrm{d}\left(v^2 \right) = 2v \,\mathrm{d}{v},代入得\begin{align}&\,\mathrm{d}\left(v^2 \right) = 2a\,\mathrm{d}{x}&(20)\\\end{align}若质点做匀加速运动,该式的物理意义是在任何一段微小时间内,速度平方的增量正比于这段时间内的位移增量.在一段时间 [t_1,t_2] 内把这些增量累加起来,就得到高中熟悉的运动学公式 \begin{align}&v_2^2-v_1^2 = 2a(x_2-x_1)&(21)\\\end{align}其中 x_1,v_1 和 x_1,v_1 分别是 t_1,t_2 时刻的位置和速度.1. 即任何一个变量值确定后,另外两个变量也随之确定2.姑且假设不会出现一个自变量对应两个函数值的情况。


二元复合函数求偏导二元复合函数求偏导是高等数学中的一个重要概念,它在微积分、统计学和金融学等领域中都有广泛应用。
本文将介绍二元复合函数求偏导的定义、求法以及应用。
一、定义二元复合函数指的是由两个变量组成的函数,例如f(x,y)=g(u,v),其中u=u(x,y)和v=v(x,y)是关于x和y的函数。
对于这样的函数,我们可以通过求偏导来研究它们的性质。
二、求法对于一个二元复合函数f(x,y)=g(u,v),我们可以通过链式法则来求它的偏导数。
具体来说,如果我们想求f关于x的偏导数,那么可以按照以下步骤进行:1. 求出u关于x的偏导数:u_x = ∂u/∂x2. 求出v关于x的偏导数:v_x = ∂v/∂x3. 将上述结果代入g中得到g_x = ∂g/∂u * u_x + ∂g/∂v * v_x4. 最后将g_x代入f中得到f_x = g_x同理,我们也可以求出f关于y的偏导数:1. 求出u关于y的偏导数:u_y = ∂u/∂y2. 求出v关于y的偏导数:v_y = ∂v/∂y3. 将上述结果代入g中得到g_y = ∂g/∂u * u_y + ∂g/∂v * v_y4. 最后将g_y代入f中得到f_y = g_y需要注意的是,这里的符号“∂”表示偏导数,而不是普通的导数。
三、应用二元复合函数求偏导在实际应用中有很多用处。
例如,在金融学中,我们可以通过求偏导来研究不同投资方案之间的收益率差异。
在微积分中,我们可以通过求偏导来研究曲面的切线和法线。
在统计学中,我们可以通过求偏导来估计参数值和预测未来趋势。
总之,二元复合函数求偏导是一个非常重要的概念,在数学和实际应用中都有广泛应用。
掌握这个概念对于提高数学素养和解决实际问题都有很大帮助。


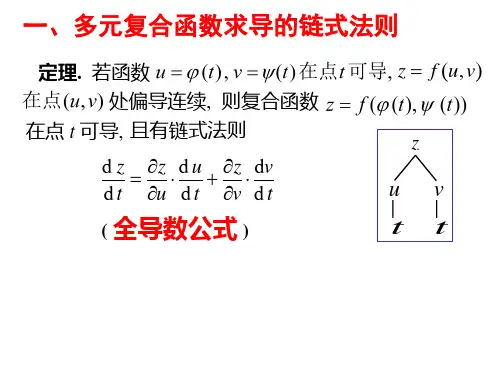
222020年第 5 期下复合函数求导中链式法则的新型理解李安玭一、复合函数的求导公式定理[1] 如果()u g x =在点x 可导,而()y f u =在点()u g x =可导,那么复合函数[()]y f g x =在点x 可导,且其导数为:()()dyf ug x dx′′=⋅或dy dy du dx du dx =⋅.这是一元复合函数的求导公式,即链式求导法则。
链式法则是隐函数、反函数以及参数方程式函数求导法的基础,对于微积分后续内容的学习有着至关重要的作用。
另一方面,链式法则的关键在于如何选取中间变量,复合函数特别是多元复合函数中间变量及自变量的复杂性,使得复合函数的求导法又成为高等数学课程的难点之一。
二、复合函数求导中常见的问题一元复合函数求导是求导运算中的基础,能够熟练地对一元复合函数进行求导,是学习二元甚至多元复合函数的偏导数以及积分等重要知识点的前提。
然而,学生在对一元复合函数进行求导时经常出现以下几种类型的问题:(一)是求导不全比如:2(sin 3)2sin 3cos3,x x x ′= 这类问题源于对基本初等函数的概念理解不透彻,导致复合函数拆分不到位。
(二)是复合运算概念模糊比如:将2sin x x 看成是由2x 与sin x 复合的函数,对其进行错误拆分,错误地运用链式法则进行计算:22(sin )()(sin )2cos x x x x x x ′′′==,出现这类问题的根本原因是没有真正理解复合运算的概念,同时没能将复合运算与混合复合函数求导是高等数学与微积分教学中的重难点,而对于复合函数的拆分与链式法则的理解是求导的关键所在,复合函数求导是高等数学与微积分中重要模块之一,它与其他模块的知识紧密联系、不可分割。
但也因此,许多学生因为没能掌握好复合函数求导的技巧与方法,导致后面的学习非常吃力,难以理解积分、多元复合函数的偏导数和高阶混合偏导数等知识点。
而对于复合函数求导,关键的是要掌握对复合函数的拆分方法,这也是对链式法则的理解与运用。
偏导的链式法则一、引言在数学中,函数的偏导数是一个重要概念,用于描述函数在某个特定点上对各个自变量的变化率。
而偏导的链式法则则是研究复合函数的导数求解方法。
这个法则在微积分、物理学、工程学等领域有着广泛的应用。
本文将深入探讨偏导的链式法则的原理和应用。
二、偏导的定义和性质2.1 偏导数的定义在多元函数中,对于一个函数f(x1,x2,...,x n),它的偏导数∂f∂x i衡量了函数在某个点关于对应自变量x i的变化率。
偏导数的定义如下:∂f ∂x i =limℎ→0f(x1,x2,...,x i−1,x i+ℎ,x i+1,...,x n)−f(x1,x2,...,x n)ℎ其中ℎ是一个趋近于零的数,表示自变量x i的一个微小变化量。
2.2 偏导数的性质偏导数具有一些重要的性质,包括:•线性性质:若函数f(x1,x2,...,x n)的偏导数存在,则对于任意实数a和b,有∂∂x i (af+bg)=a∂f∂x i+b∂g∂x i。
•交换性质:若函数f(x1,x2,...,x n)的偏导数存在,则对于任意i和j,有∂∂x i (∂f∂x j)=∂∂x j(∂f∂x i)。
这意味着偏导数的求导顺序可以交换。
三、复合函数的导数计算3.1 一元函数的复合函数导数假设函数y=f(u)和u=g(x),我们想要计算复合函数y=f(g(x))的导数。
根据链式法则,复合函数的导数可以通过各个函数的导数相乘来计算。
具体地:dy dx =dy dududx其中dydu 表示函数y对u的导数,dudx表示函数u对x的导数。
3.2 多元函数的复合函数导数对于多元函数z=f(y1,y2,...,y m)和y i=g i(x1,x2,...,x n),我们按照类似的方式计算复合函数z=f(g1(x1,x2,...,x n),g2(x1,x2,...,x n),...,g m(x1,x2,...,x n))的导数。
具体来说,可以使用偏导的链式法则来计算:∂z ∂x j =∂z∂y1∂y1∂x j+∂z∂y2∂y2∂x j+...+∂z∂y m∂y m∂x j其中∂z∂y i 表示函数z对y i的偏导数,∂y i∂x j表示函数y i对x j的偏导数。
链式法则求偏导数链式法则(Chain Rule)是微积分学中为求复合函数导数的一种常用法则。
对于一个函数 f(g(x)),其中 g(x) 是 x 的函数,而 f(u) 是 u 的函数,则它们的复合函数可以表示为:h(x) = f(g(x))那么 h(x) 的导数可以根据链式法则计算出来:h'(x) = f'(g(x)) · g'(x)其中,f'(u) 和 g'(x) 分别为 f(u) 和 g(x) 的导数。
例如,如果有函数 f(u) = u^2 和 g(x) = 3x - 1,则复合函数 h(x) = f(g(x)) = (3x - 1)^2,那么h'(x) = f'(g(x)) · g'(x) = 2(3x - 1) · 3 = 18x - 6。
链式法则是微积分学中非常重要的一个概念,它在求解多元函数的偏导数时经常会用到。
对于一个函数 z = f(x,y),如果想要求出它的偏导数∂z/∂x 和∂z/∂y,那么可以利用链式法则来计算它们:∂z/∂x = ∂f/∂x + ∂f/∂y · ∂y/∂x∂z/∂y = ∂f/∂y + ∂f/∂x · ∂x/∂y其中,∂f/∂x 和∂f/∂y 分别为 f(x,y) 对 x 和 y 的偏导数,∂y/∂x 和∂x/∂y 分别为 y 对 x 和 x 对 y 的偏导数。
例如,如果有函数 z = x^2 + y^2,其中x = r sinθ,y = r cosθ,那么可以利用链式法则求出∂z/∂r 和∂z/∂θ:∂z/∂r = ∂f/∂x · ∂x/∂r+ ∂f/∂y · ∂y/∂r = 2r sinθ · sinθ + 2rcosθ · cosθ = 2r∂z/∂θ= ∂f/∂x · ∂x/∂θ+ ∂f/∂y · ∂y/∂θ = 2r sinθ · r cosθ + 2rcosθ · (-r sinθ) = 0因此,当x = r sinθ 和y = r cosθ 时,z = x^2 + y^2 关于 r 的偏导数为 2r,关于θ的偏导数为 0。