圆柱与圆锥正交及相贯的特殊情况

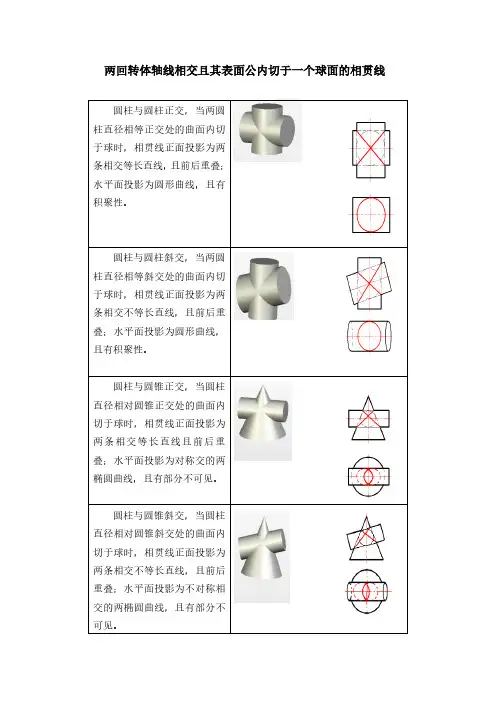
两回转体轴线相交且其表面公内切于一个球面的相贯线
圆柱与圆柱斜交，当两圆
柱直径相等斜交处的曲面内切
于球时，相贯线正面投影为两
条相交不等长直线，且前后重
叠；水平面投影为圆形曲线，
圆柱与圆锥正交，当圆柱
直径相对圆锥正交处的曲面内
切于球时，相贯线正面投影为
两条相交等长直线且前后重
叠；水平面投影为对称交的两
圆柱与圆锥斜交，当圆柱
直径相对圆锥斜交处的曲面内
切于球时，相贯线正面投影为
两条相交不等长直线，且前后
重叠；水平面投影为不对称相
交的两椭圆曲线，且有部分不。

第二节相贯线的作图求解一、轴线互相垂直的两圆柱的相贯线当圆柱体轴线垂直于投影面时，其圆柱表面在该投影面上的投影有积聚性，所以两圆柱轴线互相垂直的相贯线可利用积聚性投影取点作图法求解。

1、轴线正交两圆柱的相贯线图10－2如图10-2所示两圆柱轴线垂直相交，且分别垂直于Ｈ面和Ｗ面，因此俯视图中相贯线的投影积聚在小圆柱的投影（圆）上；左视图中相贯线的投影积聚在小圆柱两条转向轮廓线之间的大圆柱面投影（圆）上。

这样由相贯线的两个已知投影，可作出它的Ｖ面投影。

利用积聚性投影取点作图求相贯线的作图步骤如图10-3所示：图10－3 柱－柱相交相贯线作图步骤（1）求特殊点图10-3.b所示相贯线上Ｉ、Ｖ两点分别位于两圆柱对Ｖ面的转向线上，是相贯线上的最高点，也分别是相贯线上的最左点和最右点。

Ⅲ、Ⅶ两点分别位于小圆柱对Ｗ面的转向线上，它们是相贯线上的最低点，也分别是相贯线上的最前点和最后点。

在投影图上可直接作投影连线求得1’、3’、5’、7’。

（2）求一般点先在俯视图中的小圆柱投影圆上，适当地确定出若干个一般点的投影，如图10-3.c所示中的2、4、6、8等点，再按点的三面投影规律，作出Ｗ面投影2"（4"）、8" （6"）和Ｖ面投影2’（8’）4’（6’）点。

（3）判断可见性及圆滑连接由于该相贯线前后前部分对称，且形状相同，所以在Ｖ面投影中可见与不可见部分重合，按1’-2’-3’-4’-5’顺序用粗实线圆滑地连接起来。

（4）按图线要求描深各图线，完成两圆柱正交立体的三视图（图10-3.d）。

2、轴线正交内、外圆柱面的相贯线由于圆柱有实体圆柱和空心圆柱之分，因此圆柱面又有外圆柱面和内圆柱面之别。

故两圆柱面相交会产生三种情况：(1）两外圆柱面相交，如图10-4.a所示；(2）外圆柱面与内圆柱面相交，即圆柱与圆孔相交，如图10-4.b所示；(3）两内圆柱面相交，即圆孔与圆孔相交，如图10-4.c所示。

圆锥与圆柱正贯极值点图解分析文章利用两种辅助面方法分析了正交的圆锥与圆柱相贯线的求解，必求出界定相贯线范围的极限位置点。

辅助平面法只能分析求解大部分极值点，得不到极右点。

文章利用辅助球面法截圆锥和圆柱，截交线分别是两相交圆周，正面投影为两直线段。

它们交点即为相贯线上点。

利用球面越小与同轴等径的圆柱相贯线越趋右的原理，得出最小球面为求得极右点的关键。

同时给出了教材中正确解法的立体图解释。

标签：锥柱正交相贯线；极右点；辅助球面法；图解分析；最小球面1 概述求两回转体的相贯线一直是画法几何教学的难点和重点，很多教材都以求正交圆锥和圆柱相贯线作为例题讲给学生。

但对于相贯线极值点的给出却语焉不详[1-2]，有的给出做法却未分析其缘由[3-4]，有的竟给出错误解答[5-7]。

教材在引导学生学习科学方法起着至关重要的作用，例题的给出一定要使学生知其然更能知其所以然。

很多文献也对此作了研究[8-9]，但均是推导出相贯线方程，利用微分求极值的方式给出答案[10-11]。

在画法几何课堂教学，不适用长长的数学公式推导和微积分求解。

文章就投影学的方法给出相贯线极右点的求解分析。

2 辅助平面法正交锥柱相贯线求解下为很多教材出现的例题，求轴线正交的圆锥和圆柱相贯线，如图1所示。

圆柱与圆锥半贯，相贯线是一条封闭的、前后对称的空间曲线。

圆柱的轴线为侧垂线，其侧面投影积聚为圆，可根据相贯线的共有性，相贯线既在圆柱表面上又在圆锥表面。

而圆柱表面上点侧面投影都积聚在圆周上，所以相贯线侧面投影也在圆周上。

画图时不可能求出所有点的投影，只能求特殊点，这些特殊点要决定投影曲线的轮廓范围和变化趋势。

特殊点包括相贯线极限位置点和曲面立体转向轮廓线上的点。

由此在侧面投影可知其最高点1”、最低点2”和最前点3”、最后点4”。

两形体轮廓线的交点1′、2′是其正面投影。

利用辅助平面法来求相贯线的水平投影和正面投影。

如图2所示，可以求出最前，最后点的水平投影。

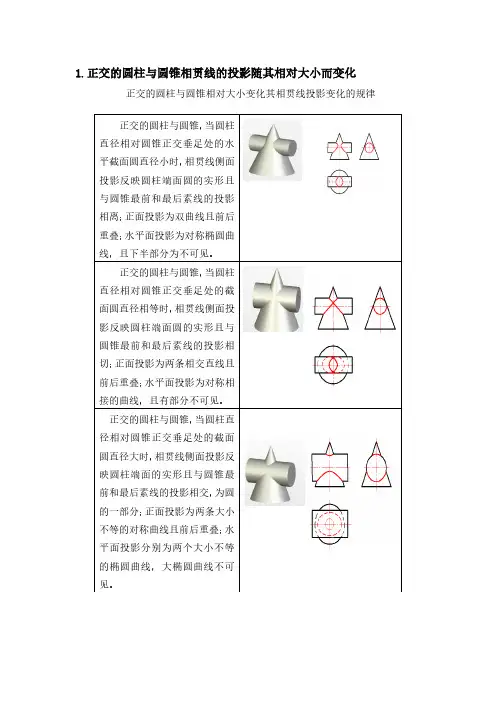
圆柱锥正交时相贯线形状分析和一重要特殊点的计算
和画法
中国舵姿的圆柱锥正交时相贯线形状分析和一重要特殊点的计算和画法总结如下：
一、形状分析
1、标准形状：中国舵姿的圆柱锥正交时相贯线的标准形状由三个部分组成：(1)圆柱形状的顶部; (2)圆锥形状的第一波形; (3)最后一波形的正交时；
2、曲率形状：圆柱锥形状的球面曲率和球面纵横比随着圆锥顶部曲率的变化而变化，而圆锥部分的曲率在圆锥中心位置最大，下降到最低点时又转换为正交时；
3、正交时形状：正交时在最后一条线段的中点出现一个特殊点，这个点是一个比较重要的特殊点；
二、特殊点计算及画法
1、坐标位置：中国舵姿的圆柱锥正交时相贯线的特殊点的坐标位置(X,Y,Z)可以通过计算得到：X=(L-2L2) Y=L2 Z=(L/2)*cosα；
2、画法：首先根据特殊点的坐标位置，先画出特殊点；然后依次在特殊点和圆锥顶点之间画出最后一条弧线，再画出一条正交线段延伸至矩形柱面，完成画法。

三、总结
总之，中国舵姿的圆柱锥正交时相贯线可以由三个部分构成：圆柱形
状的顶部，圆锥形状的第一波形和最后一波形的正交时，而正交时在
最后一条线段的中点出现一个特殊点，通过计算可以获得其坐标位置，然后进行画法构图，以完成分析和计算。

工程形体中圆锥与圆柱正交相贯的分析冯宝全【摘要】针对工程形体中常见的回转体圆锥、圆柱正交的情形做了详细探讨,对圆锥、圆柱正交的三种情形进行了解析和几何分析,为工程设计绘图提供了理论依据.文中按相离、相割及相切时三维、二维,形、图对照揭示了圆锥、圆柱正交之相贯线及其投影的本来面目.【期刊名称】《机械工程师》【年(卷),期】2016(000)007【总页数】3页(P18-20)【关键词】工程形体;圆锥;圆柱;相贯;设计绘图【作者】冯宝全【作者单位】沈阳汽车工业学院,沈阳110015【正文语种】中文【中图分类】TH122工程形体中常见回转体圆锥、圆柱正交的情形，要弄清楚它们及组合的几何性质，分析时就得将其从工程形体中抽象出来，因为直接用工程形体来讨论，会由于形体上的复杂和困难而转移了解题目标。

正交是指这两回转体轴线垂直相贯，这状况是一种形，工程设计与制造要用到“形→图”和“图→形”之间的转换。

图是形在画面上的展现，在画法几何学科中，求解圆锥与圆柱的正交——表面交线为相贯线，通常运用投影的积聚性、辅助平面及辅助球面两种方法将三维形用二维图表示。

但设计时仅掌握画法几何原理，按这两种方法设计绘图，往往对圆锥与圆柱正交相贯线的投影形状、变化趋势及其特殊点的位置等把握不准，因为画法几何与数学上的几何有所不同，前者的理论基础是投影几何，是用几何方法处理几何问题，更多的是从空间概念形象地去审视，而后者则偏重于解析方法。

我们主张，不可过多地依赖直观感觉，应多使用数学思维方式，来揭示相贯线投影的本来面目，本文力求考虑如何将其化成代数方程（公式），来分析它的过程与结果。

圆锥和圆柱都是空间曲面，它们的相贯线为空间曲线。

要想正确画出该曲线的投影图，就必须搞清楚其空间的形，即圆锥与圆柱的位置关系[1]。

设正交相贯的圆锥半顶角为θ、圆柱半径为R、圆柱轴心线到锥顶的距离为c,从圆锥圆柱的侧面投影图上可看出它们的位置关系有三种情况：1）相离。

圆柱贯穿圆锥正交相贯线的一种几何作法作者：余敏来源：《课程教育研究·上》2014年第12期【摘要】找准、找全特殊点，是快速、准确地作出相贯线的关键。

本文基于数学理论，运用数学模型，针对圆柱贯穿圆锥正交相贯线上特殊点不能准确画出的问题，提出了一种准确、简便、可靠的几何作法，为手工绘图、计算机绘图提供了理论依据。

【关键词】数学模型圆柱圆锥正交相贯线【中图分类号】G64 【文献标识码】A 【文章编号】2095-3089（2014）12-0123-02一、引言制图中求两个回转曲面的相贯线，通常是先确定特殊点，再根据需要找出一些中间点，然后用光滑曲线连接起来。

本文基于数学理论，运用数学模型，针对圆柱贯穿圆锥正交相贯线上最右（左）点不能准确画出的问题，提出了一种准确、简便、可靠的几何作法，也为手工绘图、计算机绘图提供了理论依据。

二、建立圆柱贯穿圆锥正交相贯线上的数学模型圆柱贯穿圆锥且轴线垂直正交，设圆柱的半径为r，圆锥的半顶角为，圆柱与圆锥轴线的交点为坐标原点O，圆锥顶点S到O点的距离为h，如图1建立空间直角坐标系Oxyz，于是有圆柱面方程：y2+z2= r2 （1）圆锥面方程：x2+y2=（z-h）2tan2 （2）将上述两方程联立，消去y，得相贯线方程：x2+r2-z2=（z-h）2tan2 （3）（一）解析法确定圆柱贯穿圆锥正交相贯线的形状将相贯线方程（3）化简，整理得：-（z-hsin2 ）2 =h2sin2 cos2 -r2cos2 （4）由于是圆柱贯穿圆锥，所以r0，所以方程（4）表示的是左、右两支双曲线，在xoz平面上，z轴是虚轴，z=h sin2 是实轴，顶点在实轴上。

即当圆柱贯穿圆锥正交时，二者相贯线在xoz平面上的投影为左右对称的双曲线。

由（4）不难求得左支双曲线的顶点B坐标为（，0，hsin2 ）。

（二）导数法证明圆柱贯穿圆锥正交相贯线上最右点即为上述左支双曲线的顶点将相贯线方程（3）化简，得x2=z2sec2 -2zh tan2 +h2tan2 -r2 （5）对（5）式两边求关于z的导数，得2x =2z sec2 -2h tan2 令 =0，得驻点z = h sin2？夼.在只考虑左支双曲线时，有x > 0。