第7课 圆柱和圆锥相贯线

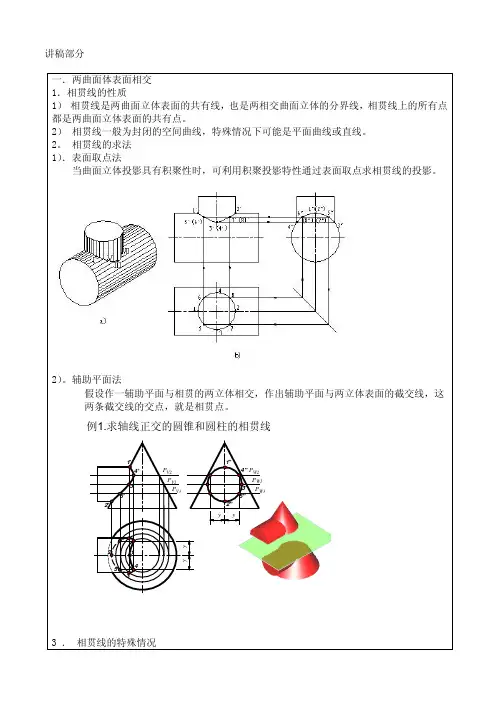
讲稿部分
在一般情况下，两曲面立体的相贯线为空间曲线，但在特殊情况下为平面曲线。

1 ）两同轴回转体相交，其相贯线为垂直轴线的圆，当回转体轴线平行于某一投影面时，则相贯线在该投影面上的投影为垂直于轴线的直线，如图 5-1
2 所示。

2 ）两轴线平行的圆柱相交，其相贯线为平行于轴线的直线，如图 5-1
3 所示。

3 ）当相交两回转体同时切于一个球面时，其相贯线为椭圆。

如果两回转体轴线都平行于某一投影面时，则相贯线在该投影面上的投影为两条相交直线，如图 5-13 所示。

4．解题步骤
1）分析
（1）空间分析；
（2）投影分析。

2）作图
（1）求点；
（2）连线；
（3）补全轮廓线；
（4）加深最后结果。

圆柱与圆锥正交及相贯的特殊情况1．圆柱与圆锥正交作圆柱与圆锥正交的相贯线的投影，通常要用辅助平面法作出一系列点的投影。

辅助平面法的原理是基于三面共点原理。

如图4-24，圆柱与圆锥台正交，作一水平面P ，平面P 与圆锥的截交线（圆）和平面P 与圆柱面的截交线（两平行直线）相交，交点Ⅱ、IV 、VI 、Ⅷ既是圆锥面上的点，也是圆柱面上的点，又是平面P 上的点（三面共点），即是相贯线上的点。

用来截切两相交立体的平面P ，叫做辅助平面。

图4-24 三面共点为了方便、准确地求得共有点，辅助平面的的选择原则是：辅助平面与两立体表面的交线的投影，为简单易画的图形（直线或圆）。

通常大多选用投影面平行面为辅助平面。

例1：如图4-25b 所示，圆锥台与圆柱轴线正交，求作相贯线的投影。

解：由于两轴线垂直相交，相贯线是一条前后、左右对称的封闭的空间曲线，其侧面投影为圆弧，重合在圆柱的侧面投影上，需作出的是其水平投影和正面投影。

作图步骤如下：1）作特殊点。

根据侧面投影1”、3”、（5”）、7”可作出正面投影l’、3’、5’、（7’）和水平投影1、3、5、7，如图4-25c 所示。

其中I 、V 点是相贯线上的最左、最右（也是最高）点，Ⅲ、Ⅶ点是相贯线上的最前、最后（也是最低）点。

2）求作一般位置点。

在最高点和最低点之间作辅助平面P （水平面），它与圆锥面的交线为圆，与圆柱面的交线为两平行直线，它们的交点Ⅱ、Ⅳ、Ⅵ、Ⅷ即为相贯线上的点。

先作出交线圆的水平投影，再由2”(4”)、8”(6”)作出2、4、6、8，进而作出2’(8’)和4’（6’）, 如图4-25d 所示。

3）判别可见性，光滑连线。

相贯线前后对称，前半相贯线的正面投影可见；相贯线的水。

第二节相贯线的作图求解一、轴线互相垂直的两圆柱的相贯线当圆柱体轴线垂直于投影面时，其圆柱表面在该投影面上的投影有积聚性，所以两圆柱轴线互相垂直的相贯线可利用积聚性投影取点作图法求解。

1、轴线正交两圆柱的相贯线图10－2如图10-2所示两圆柱轴线垂直相交，且分别垂直于Ｈ面和Ｗ面，因此俯视图中相贯线的投影积聚在小圆柱的投影（圆）上；左视图中相贯线的投影积聚在小圆柱两条转向轮廓线之间的大圆柱面投影（圆）上。

这样由相贯线的两个已知投影，可作出它的Ｖ面投影。

利用积聚性投影取点作图求相贯线的作图步骤如图10-3所示：图10－3 柱－柱相交相贯线作图步骤（1）求特殊点图10-3.b所示相贯线上Ｉ、Ｖ两点分别位于两圆柱对Ｖ面的转向线上，是相贯线上的最高点，也分别是相贯线上的最左点和最右点。

Ⅲ、Ⅶ两点分别位于小圆柱对Ｗ面的转向线上，它们是相贯线上的最低点，也分别是相贯线上的最前点和最后点。

在投影图上可直接作投影连线求得1’、3’、5’、7’。

（2）求一般点先在俯视图中的小圆柱投影圆上，适当地确定出若干个一般点的投影，如图10-3.c所示中的2、4、6、8等点，再按点的三面投影规律，作出Ｗ面投影2"（4"）、8" （6"）和Ｖ面投影2’（8’）4’（6’）点。

（3）判断可见性及圆滑连接由于该相贯线前后前部分对称，且形状相同，所以在Ｖ面投影中可见与不可见部分重合，按1’-2’-3’-4’-5’顺序用粗实线圆滑地连接起来。

（4）按图线要求描深各图线，完成两圆柱正交立体的三视图（图10-3.d）。

2、轴线正交内、外圆柱面的相贯线由于圆柱有实体圆柱和空心圆柱之分，因此圆柱面又有外圆柱面和内圆柱面之别。

故两圆柱面相交会产生三种情况：(1）两外圆柱面相交，如图10-4.a所示；(2）外圆柱面与内圆柱面相交，即圆柱与圆孔相交，如图10-4.b所示；(3）两内圆柱面相交，即圆孔与圆孔相交，如图10-4.c所示。

圆柱贯穿圆锥正交相贯线的一种几何作法作者：余敏来源：《课程教育研究·上》2014年第12期【摘要】找准、找全特殊点，是快速、准确地作出相贯线的关键。

本文基于数学理论，运用数学模型，针对圆柱贯穿圆锥正交相贯线上特殊点不能准确画出的问题，提出了一种准确、简便、可靠的几何作法，为手工绘图、计算机绘图提供了理论依据。

【关键词】数学模型圆柱圆锥正交相贯线【中图分类号】G64 【文献标识码】A 【文章编号】2095-3089（2014）12-0123-02一、引言制图中求两个回转曲面的相贯线，通常是先确定特殊点，再根据需要找出一些中间点，然后用光滑曲线连接起来。

本文基于数学理论，运用数学模型，针对圆柱贯穿圆锥正交相贯线上最右（左）点不能准确画出的问题，提出了一种准确、简便、可靠的几何作法，也为手工绘图、计算机绘图提供了理论依据。

二、建立圆柱贯穿圆锥正交相贯线上的数学模型圆柱贯穿圆锥且轴线垂直正交，设圆柱的半径为r，圆锥的半顶角为，圆柱与圆锥轴线的交点为坐标原点O，圆锥顶点S到O点的距离为h，如图1建立空间直角坐标系Oxyz，于是有圆柱面方程：y2+z2= r2 （1）圆锥面方程：x2+y2=（z-h）2tan2 （2）将上述两方程联立，消去y，得相贯线方程：x2+r2-z2=（z-h）2tan2 （3）（一）解析法确定圆柱贯穿圆锥正交相贯线的形状将相贯线方程（3）化简，整理得：-（z-hsin2 ）2 =h2sin2 cos2 -r2cos2 （4）由于是圆柱贯穿圆锥，所以r0，所以方程（4）表示的是左、右两支双曲线，在xoz平面上，z轴是虚轴，z=h sin2 是实轴，顶点在实轴上。

即当圆柱贯穿圆锥正交时，二者相贯线在xoz平面上的投影为左右对称的双曲线。

由（4）不难求得左支双曲线的顶点B坐标为（，0，hsin2 ）。

（二）导数法证明圆柱贯穿圆锥正交相贯线上最右点即为上述左支双曲线的顶点将相贯线方程（3）化简，得x2=z2sec2 -2zh tan2 +h2tan2 -r2 （5）对（5）式两边求关于z的导数，得2x =2z sec2 -2h tan2 令 =0，得驻点z = h sin2？夼.在只考虑左支双曲线时，有x > 0。

正交圆柱圆锥相贯线最右点的确定及证明正交圆柱圆锥相贯线正是指两个正交圆柱相贯穿圆锥。

一般情况下，正交圆柱圆锥相贯线右侧点位于正交圆柱任一圆面上，即使它是相贯穿圆锥的最右点。

今天，我们就来讨论对正交圆柱的最右点的确定及证明。

要确定正交圆柱的最右点，必须使用交叉圆半径方程和交叉储帧方程。

这两个方程可以帮助我们计算出正交圆柱的圆半径和其有关的框架信息。

我们将其程序及表达式如下：当正交圆柱圆锥相贯穿时，正交圆柱的最右点就位于正交圆柱任一圆面上，如下图所示。

从图中可以看出，正交圆柱的最右点是有一定模式的。

首先，它位于一个正交圆柱任一圆面上，并且由竖直方向分布。

其次，它还位于一条直线上，这条直线是以正交圆柱两圆面的中心点为中心画出来的。

例如，在以下正交圆柱圆锥相贯穿示例中，可以看到C和G 的位置就在最右点位置上。

为了证明这一结论，我们可以通过使用交叉圆半径方程来求解正交圆柱的圆半径并计算正交圆柱的最右点。

首先，使用交叉圆半径方程，根据正交圆柱的半径r、内径D及内螺距p计算出它的外径R：外径R=r+D+2*p再把外径R的值带入交叉储帧方程：F=2*r(r+D)+2*p^2根据帧的外径R和其内径D的关系，我们可以得出正交圆柱的最右点为：C=R+D最后，我们为这一结果证明：在此实例中，正交圆柱的半径为10，内径为6，内螺距为2，外径为：外径R=10+6+2*2=20交叉质量储存：F=2*10(10+6)+2*2^2=220最右点：C=20+6=26根据上述结果，我们可以证实正交圆柱的最右点正是位于正交圆柱任一圆面上，且是相贯穿圆锥的最右点。

我们今天已讨论完正交圆柱圆锥相贯线最右点的确定及证明。

结果证明，正交圆柱的最右点位于正交圆柱任一圆面上，是相贯穿圆锥的最右点。

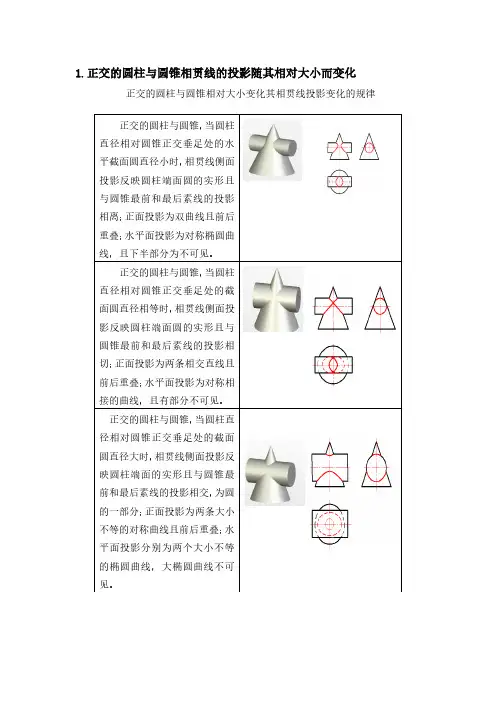
柱锥斜交相贯线解析性质分析与特殊点图解方法
刘敏;林犀;冯涓
【期刊名称】《图学学报》
【年(卷),期】2014(035)005
【摘要】轴线相交的圆柱和圆锥两立体相交时,一般情况下会产生两条相贯线.文章分析了在圆柱、圆锥正交和圆柱、圆锥斜交情况下,相贯线随圆柱半径变化而形成的不同形状和特殊点性质.进一步结合解析形式分析,推导了圆柱、圆锥轴线相交并产生左右两条相贯线时,两条相贯线上最里点的分布规律;相贯线形状与圆柱半径取值范围的精确对应关系;并给出了确定相贯线上最里点的辅助球半径公式.最后,文章依据以上结果提出了圆柱、圆锥斜交时相贯线上所有特殊点的图解方法.
【总页数】8页(P682-689)
【作者】刘敏;林犀;冯涓
【作者单位】清华大学机械工程系,北京100084;清华大学土木工程系,北京100084;清华大学机械工程系,北京100084
【正文语种】中文
【中图分类】TB23
【相关文献】
1.圆柱锥正交时相贯线形状分析和一重要特殊点的计算和画法 [J], 赵国华
2.柱锥斜交相贯线解析性质分析与特殊点图解方法 [J], 刘敏;林犀;冯涓;
3.正交球锥在特殊情形下相贯线最右点误差分析 [J], 邓东芳
4.关于轴线斜交的圆柱面与圆锥面相贯线上特殊点的探讨 [J], 李琦;刘兴家
5.圆柱与圆锥,圆锥与圆球相贯线特殊点的解析和图解 [J], 王树胜;王树忠
因版权原因，仅展示原文概要，查看原文内容请购买。

圆柱体斜交相贯线计算圆柱体是一种常见的几何体，具有圆形底面和侧面，而斜交相贯线是指两个圆柱体在一定角度下相交形成的线段。

本文将介绍圆柱体斜交相贯线的计算方法和相关应用。

1. 圆柱体斜交相贯线的定义和特点圆柱体斜交相贯线，是指两个圆柱体在一个平面上以一定斜角相交而形成的线段。

它与圆柱体的高度、底面半径、斜角等因素有关。

2. 圆柱体斜交相贯线的计算方法圆柱体斜交相贯线的计算需要考虑以下因素：2.1 圆柱体的参数首先，我们需要知道两个圆柱体的底面半径和高度。

假设圆柱体A 的底面半径为r1，高度为h1；圆柱体B的底面半径为r2，高度为h2。

2.2 斜交角度斜交角度是两个圆柱体相交的角度。

假设斜交角度为α，其中0°< α < 90°。

2.3 斜交位置斜交位置是指两个圆柱体相交的位置。

它可以是在底面上的某点，也可以是在侧面上的某条线段。

基于以上参数，计算圆柱体斜交相贯线的方法如下：步骤1：求出两圆柱体底面的相交圆的半径。

- 如果两个圆柱体的底面相切，则相交圆半径为0；- 如果两个圆柱体底面不相切，则可以利用几何关系求得相交圆半径。

步骤2：根据斜交角度和相交圆半径，可以计算出两个圆锥体相交的高度。

步骤3：利用勾股定理，计算出两圆柱体斜交相贯线的长度。

3. 圆柱体斜交相贯线的应用圆柱体斜交相贯线的计算方法在工程设计、建筑设计和计算机图形学等领域具有重要应用。

在工程设计中，圆柱体斜交相贯线的计算可以帮助工程师更准确地确定两种材料、部件或结构的相交位置和尺寸，在设计和生产过程中起到重要作用。

在建筑设计中，圆柱体斜交相贯线的计算可以应用于弧形建筑物的设计和建造，如拱形天花板、拱门等。

在计算机图形学中，圆柱体斜交相贯线的计算可以用于实现真实感渲染和三维建模等方面，为计算机生成的图形提供精确的几何表达。

综上所述，圆柱体斜交相贯线的计算方法是基于两个圆柱体的底面半径、高度和斜交角度，结合几何关系和勾股定理进行计算。