ch2_2.3.2正态分布下的Bayes判据的判别函数和决策面(线性、二次分类器)
- 格式:ppt
- 大小:649.00 KB
- 文档页数:29

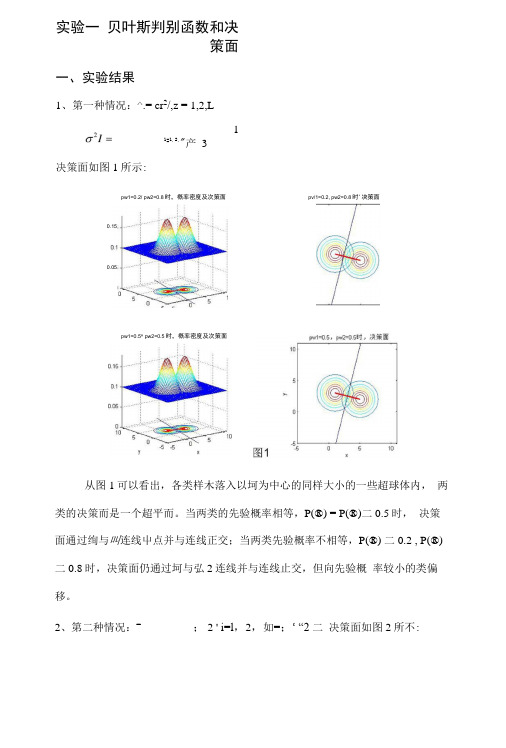
实验一贝叶斯判别函数和决策面一、实验结果1、第一种情况:^.= cr2/,z = 1,2,L决策面如图1所示:从图1可以看出,各类样木落入以坷为中心的同样大小的一些超球体内,两类的决策而是一个超平而。
当两类的先验概率相等,P(®) = P(®)二0.5时,决策面通过绚与叫连线屮点并与连线正交;当两类先验概率不相等,P(®) 二0.2 , P(®)二0.8时,决策面仍通过坷与弘2连线并与连线止交,但向先验概率较小的类偏移。
2、第二种情况:=; 2 ' i=l,2,如=;‘ “2 二决策面如图2所不:pv/1=0.2, pw2=0.8时'决策面pw1=0.2/ pw2=0.8时,槪率密度及次策面0.150.05pw1=0.5^ pw2=0.5时,槪率密度及次策面11=1,2,"产3从图2可以看出,各类样木落入以冷为中心的同样大小的一些超椭球内,两 类的决策面是一个超平面。
当两类的先验概率相等,P(®)二P(®)二0.5时,决 策血通过旳与u 2连线中点;当两类先验概率不相等,戶(©)二0・2,卩(5)二0・8 时,决策面仍通过绚与“2连线,但向先验概率较小的类偏移。
3、第三种情况: ,z, j = 1,2,L ,c'5 0__1 0_T_5_,11\ —,=0 5_厶2_0 11_3_Z_3_pw1=0.2, pw2=0.8时,槪潔密度及决策面pw1=0.2, pw2=0.8时,块策面pw1=0.5. pv/2=05时,槪潔密度及决策面如图3-1所示,当各个随机变量的方差类内相等、类间不相等时,决策而是是一个超球面,投影是圆,且将方差较小的类包围。
当两类先验概率和等时,决策面过吗与“2连线屮点,当两类先验概率不相等时,决策而偏向先验概率小 的类。
1u x =13如图3-2所示,当两个随机变量各类方差都不相等时,概率密度曲线是椭圆, 决策面也是椭圆。

两类正态分布模式的贝叶斯判别硕633 3106036072 赵杜娟一.实验目的1.理解贝叶斯判别原则,编写两类正态分布模式的贝叶斯分类程序; 2.了解正态分布模式的贝叶斯分类判别函数; 3.通过实验,统计贝叶斯判别的正确率。
二.实验原理(1)贝叶斯判别原则对于两类模式集的分类,就是要确定x 是属于1ω类还是2ω类,这要看x 来自1ω类的概率大还是来自2ω类的概率大,根据概率的判别规则,可以得到: 如果)|()|(21x P x P ωω> 则 1ω∈x如果)|()|(21x P x P ωω< 则 2ω∈x (1.1) 利用贝叶斯定理,可得 )()()|()|(x p P x p x P i i i ωωω=式中,)|(i x p ω亦称似然函数。
把该式代入(1.1)式,判别规则可表示为: )()|()()|(2211ωωωωP x p P x p > 则 1ω∈x )()|()()|(2211ωωωωP x p P x p < 则 2ω∈x 或写成: )()()|()|()(122112ωωωωP P x p x p x l >=则 1ω∈x )()()|()|()(122112ωωωωP P x p x p x l <=则 2ω∈x (1.2) 这里,12l 称为似然比,2112)()(θωω=P P 称为似然比的判决阈值。
该式称为贝叶斯判别。
(2)正态分布模式的贝叶斯分类器判别原理具有M 种模式类别的多变量正态分布的概率密度函数为:)]()(21exp[)2(1)|(1212i i T i in i m x C m x C x P ---=-πω 2,1=i (1.3)式中,x 是n 维列向量; i m 是n 维均值向量; i C 是n n ⨯协方差矩阵;i C 为矩阵i C 的行列式。
且有 {}i i m E x =; ()(){}Ti i i i m x m x E C --=;{}iE x 表示对类别属于i ω的模式作数学期望运算。



实验十一Bayes判别实验目的和要求掌握Bayes判别分析的理论与方法、模型的建立与误差率估计;掌握利用判别分析的SAS过程解决有关实际问题.实验要求:编写程序,结果分析.实验内容:5.4 5.5 选一题data examp5_4。
input group $ x1-x7 @@。
cards。
G1 6.6 39 1.0 6.0 6 0.12 20G1 6.6 39 1.0 6.0 12 0.12 20G1 6.1 47 1.0 6.0 6 0.08 12G1 6.1 47 1.0 6.0 12 0.08 12G1 8.4 32 2.0 7.5 19 0.35 75G1 7.2 6 1.0 7.0 28 0.30 30G1 8.4 113 3.5 6.0 18 0.15 75G1 7.5 52 1.0 6.0 12 0.16 40G1 7.5 52 3.5 7.5 6 0.16 40G1 8.3 113 0.0 7.5 35 0.12 180G1 7.8 172 1.0 3.5 14 0.21 45G1 7.8 172 1.5 3.0 15 0.21 45G2 8.4 32 2.0 9.0 10 0.35 75 G2 8.4 32 2.5 4.0 10 0.35 75 G2 6.3 11 4.5 7.5 3 0.20 15 G2 7.0 8 4.5 4.5 9 0.25 30 G2 7.0 8 6.0 7.5 4 0.25 30 G2 7.0 8 1.5 6.0 1 0.25 30 G2 8.3 161 1.5 4.0 4 0.08 70 G2 8.3 161 0.5 2.5 1 0.08 70 G2 7.2 6 3.5 4.0 12 0.30 30 G2 7.2 6 1.0 3.0 3 0.30 30 G2 7.2 6 1.0 6.0 5 0.30 30 G2 5.5 6 2.5 3.0 7 0.18 18 G2 8.4 113 3.5 4.5 6 0.15 75 G2 8.4 113 3.5 4.5 8 0.15 75 G2 7.5 52 1.0 6.0 6 0.16 40 G2 7.5 52 1.0 7.5 8 0.16 40 G2 8.3 97 0.0 6.0 5 0.15 180 G2 8.3 97 2.5 6.0 5 0.15 180 G2 8.3 89 0.0 6.0 10 0.16 180 G2 8.3 56 1.5 6.0 13 0.25 180 G2 7.8 172 1.0 3.5 6 0.21 45run。