第四章(4)非线性判别函数
- 格式:ppt
- 大小:781.50 KB
- 文档页数:69


第4章 线形判别函数在第1章中,说明了模式的概念,它是取自客观世界中的一次抽样试验样本的被测量值的综合。
如果试验对象和测量条件相同,所有测量值具有重复性,即在多次测量中,它们的结果不变,获得的模式称为确定性的模式。
否则,测量值是随机的,这样的模式称为随机性的模式,简称随机模式。
下面介绍确定性模式的分类方法。
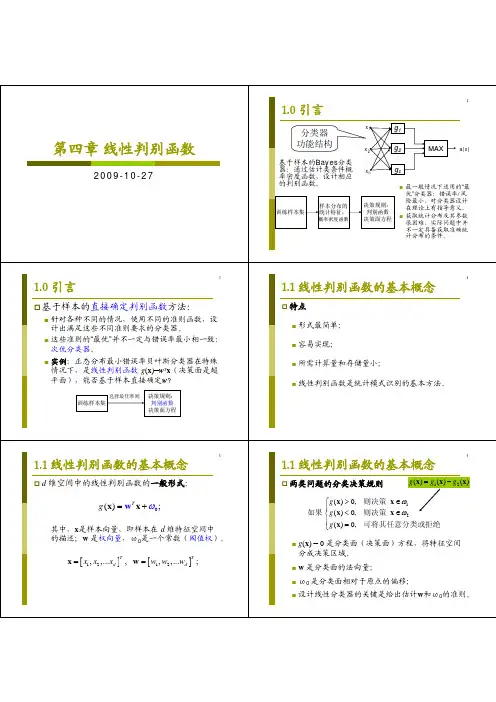
4.1 线形判别函数的基本概念在前面两章中讨论的分类器设计方法,是在已知类条件概率密度)|(i w x P 和先验概率)(i w P 的条件下,用Bayes 定理求出后验概率)|(x w P i ,并根据后验概率的大小进行分类决策。
在解决实际问题时,类条件概率密度)|(i w x P 很难求出,用非参数估计方法又需要大量的样本。
实际上我们可以不求)|(i w x P ,而是利用样本集直接设计分类器,也就是先给定某个判别函数类,然后利用样本集确定判别函数中的未知参数。
这种方法针对不同的要求,所设计出的分类器应尽可能地满足这些要求,这个“尽可能好”的结果对应于判别准则函数取最优值。
前两章的Bayes 分类器,是使错误率或风险达到最小的分类器,通常称这种分类器为最优分类器。
相对而言其它准则函数下得到的分类器就是“次优”的了。
采用线性判别函数所产生的错误率或风险虽然比Bayes 分类器要大,但是线性判别简单、易实现、且需要的计算量和存储量小,所以线性判别函数是统计模式识别的基本方法之一,也是实际中最常用的方法之一。
在一个d 维的特征空间中,Tdx x x x ),...,,(21 ,线性判别函数的一般表达式如下:1d d d 2211 g(x )+++⋯++=w x w x w x w其中,1w ,2w ,…1+d w 为加权因子,或称为系数,若令:T d w w w w ),....,,(21=,称为加权量,则: 1)(++=d T w x w x g若令:T d x x x x )1,,....,,(21=,称为增广模式。




第四章非线性微分代数系统的局部结构理论本章主要目的在于从定性的角度研究平衡点的局部性态。
第1节介绍微分代数系统指数的概念及其数学基本结构。
第2节首先考察线性微分代数系统中的一个带根本性的问题,即其广义特征根与其向量场的特征根的等价性问题。
然后,在此基础上我们依据广义特征根对对余二维线性违反微分代数系统的平衡点(奇点)作出了全面分类。
第3节考虑非线性微分代数系的线性近似问题,主要研究非线性微分代数系统与线性微分代数系统的局部拓扑等价性。
第4节研究非线性微分代数系统的局部参数化问题,给出受限系统的最小状态空间形式,其内容主要是为第5节讨论线性近似为中心的情形以及微分代数系统的分支问题做准备的。
第5节通过取定系统状态空间形式,利用后继函数判别法和形式级数判别法给出中心..焦点的判别法则和算法步骤。
第6节考察一个具体微分代数系统局部性态,作为第4和第5节中的方法和结果的应用4.1 微分代数系统的指数和数学结构由于微分代数系统由微分方程和代数方程混合而成,我们总希望通过微分运算把微分代数系统化显示常微分方程的形式。
在这种变换过程中所用到的微分次数称之为微分代数系统的指数,这样,微分方程有指数0。
在给出微分代数系统的指数的精确定义之前,我们考察余下几个简单的例子。
例题4.1 设()q t 是一个给定的光滑函数,如下关于变量y 的纯量方程()y q t = (1.1) 是一个指数1的微分代数方程,这是由于对(1.1)式两边微分一次就可把纯量方程(1.1)化为关于纯量y 显示微分方程。
系统121()y q t y y ='= (1.2)是指数2系统。
事实上,先对第一个方程微分得21()y y q t ''== 再对上式微分得21()y y q t '''''== 通过两次微分运算得到微分方程12()()y q t y q t ''='''= 类似地,通过三次微分运算可以把系统3()u q t y u =''= (1.3) 化为3y 的微分方程,因此,系统(1.3)有指数3.非线性微分代数系统一般形式由如下隐式形式给出(,,)0F t y y '= (1.4) 其中Jacobian 矩阵函数/F y '∂∂可以是奇异的。




∙∙∙x 2x ω∈则决策1.2 广义线性判别函数
10
1.2 广义线性判别函数
☐例:如
x =[x 1, x 2]T ,二次判别函数为
⏹
定义则可找到a ,a 0,使()T g c B A =++x x x x ;
22
1212
12[,,,,],T x x x x x x =y 0'()().
T g a g =+≡y a y x
13
1.2 广义线性判别函数
☐举例:设在三维空间中一个类别分类问题拟采用
二次曲面。
如采用广义线性方程求解,试求其广
义样本向量与广义权向量的表达式,及其维数。
Fisher准则的描述:用投影后数据的统计性质—
均值和离散度的函数作为判别优劣的标准。
1220;02w S S S ⎡⎤
=+=⎢⎥
⎣⎦
Fisher准则最佳投影
3. 感知准则函数
对于任何一个增广权向量a 求解增广权向量的算法收敛到解区的边界。
批量样本修正法与单样本修正法
单样本修正法:样本集视为不
断重复出现的序列,逐个样本
批量样本修正法:样本成批或
41。