基于李雅普诺夫方法设计的模型参考自适应系统Matlab仿真

多轴同步收放卷系统建模与自适应控制石贤可;温盛军【摘要】针对工业生产中广泛存在的张力控制问题,以西门子系列PLC和变频器组成的多轴同步收放卷系统为研究对象,采用动力学建模方法,建立了收放卷系统的动力学模型,并基于该模型设计了以李雅普诺夫稳定性理论为依据的模型参考自适应张力控制器.MATLAB仿真和实验均表明,与PID控制器相比,该模型参考自适应张力控制器在系统启动、升速以及减速阶段均具有更好的动态性能和鲁棒性.【期刊名称】《中原工学院学报》【年(卷),期】2019(030)003【总页数】8页(P82-89)【关键词】多轴同步;张力控制;模型参考自适应;李雅普诺夫【作者】石贤可;温盛军【作者单位】中原工学院电子信息学院,河南郑州 450007;中原工学院中原彼得堡航空学院,河南郑州 450007【正文语种】中文【中图分类】TP273多轴同步收放卷系统是工业现场中经常使用的电气控制系统，收放卷系统在钢铁厂、造纸厂、印刷厂、纺织漂染厂、食品厂、燃料电池厂应用广泛，涉及轧制、拉拔、压花、涂层、印染、清洗以及卷绕等工序，其作用是控制卷材的张力，使其保持稳定[1]。

曾有学者利用动力学建模方法得出了多轴同步收放卷系统开卷机构的数学模型，并认为，多轴同步收放卷系统张力控制的关键是解决速度对张力影响较大的问题[2-3]。

陈耀等针对PID (Proportion Integration Differentiation)算法不能解决控制模型突变时动态响应不佳问题，设计了模糊PID控制器[4]。

马文明等研究了内模控制算法在多轴同步张力控制系统中的应用[5]。

智能控制算法在多轴同步张力控制系统中的应用，从不同程度上解决了张力控制系统存在的问题。

本文通过推导多轴同步收放卷系统的数学模型，设计基于模型参考自适应算法的张力控制器，试图解决以PID算法为张力控制器时系统启动、升减速阶段存在的张力波动过大问题；并且将该控制器应用于收放卷系统，采集相关数据，观察收放卷系统升减速阶段的张力变化，以确定该控制器的应用效果。

基于分数阶参考模型的半主动悬架自适应控制摘要：基于分数阶微积分理论，提出一个以含分数阶次力与位移传递函数定义的悬架为参考模型的磁流变阻尼半主动控制悬架自适应控制模型。

通过最优控制方法得到参考悬架的最佳参数，由于分数阶微积分的引入，使得参考模型更加精确。

采用李雅普诺夫稳定性理论设计得到模型参考自适应控制的自适应控制律，并用Oustaloup逼近算法解算分数阶微积分因子。

Matlab/Simulink仿真结果表明，与传统的被动悬架相比，悬架的平顺性和舒适性有一定的提高，且能保证一定的系统鲁棒性，但悬架动位移稍有增大。

关键词：悬架分数阶自适应控制仿真中图分类号：TP13；U461.4 文献标识码：A 文章编号：1674-098X（2015）12（a）-0244-04Abstract：According to the fractional calculus theory，an adaptive control model of a semi-active control suspension with magneto rheological （MR）damping is established ，which the reference suspension model is defined a fractional force and displacement transfer function. The optimal parameters of the reference suspension are obtained by the optimal control method. Due to the introduction of fractional calculus，makesthe reference model more accurate. A model reference adaptive control method based on Lyapnov stability theory is used to design adaptive controller，and the solution of fractional calculus factor is realized by the Oustaloup’s approximation algorithm. The Matlab/Simulink simulation results indicate that，compared with the traditional passive suspension，the primary performances of the new suspension is improved and the system robustness can be guaranteed，but the suspension dynamic displacement increased slightly.Key Words：Fractional Order；adaptive Control；Simulation；Suspension20世纪90年代初法国Alain Oustaloup教授[1]基于分数阶传递函数具有等相位特性提出的一种鲁棒控制理论（即“Commmande Robuste d’Ordre Non Entier”，其中CRONE是其首字母缩写）。

基于李雅普诺夫方法设计的模型参考自适应系统Matlab仿真
基于李雅普诺夫方法设计的模型参考自适应系统Matlab 仿真
一、未加入控制器的系统
其中，上半部分为参考模型，下半部分为控制系统，分别使用阶跃信号和方波信号输入，便可得到相应的输出。

1. 阶跃信号下的输出
2. 方波信号下的输出
仿真时间（s ）
幅值
阶跃输入
仿真时间（s ）
幅值
广义状态误差
仿真时间（s ）
幅值控制对象状态变量
二、加入了自适应控制器的系统
其中，上半部分为参考模型，下半部分为控制系统，仍然使用和先前相同的阶跃信号和方波信号输入，便可得到相应的输出。

仿真时间（s ）
幅值
广义状态误差
仿真时间（s ）
幅值
控制对象状态变量
仿真时间（s ）
幅值
方波输入
1. 阶跃信号下的输出
2. 方波信号下的输出
使用李雅普诺夫方法设计自适应控制器后，可以看到系统的误差明显减小了，同时系统的稳定性也得到了提升。

仿真时间（s ）幅值
广义状态误差
仿真时间（s ）幅值
广义状态误差
仿真时间（s ）幅值
控制对象状态变量
仿真时间（s ）幅值
控制对象状态变量。

基于MATLAB控制系统的仿真与应用毕业设计论文目录一、内容概括 (2)1. 研究背景和意义 (3)2. 国内外研究现状 (4)3. 研究目的和内容 (5)二、MATLAB控制系统仿真基础 (7)三、控制系统建模 (8)1. 控制系统模型概述 (10)2. MATLAB建模方法 (11)3. 系统模型的验证与校正 (12)四、控制系统性能分析 (14)1. 稳定性分析 (14)2. 响应性能分析 (16)3. 误差性能分析 (17)五、基于MATLAB控制系统的设计与应用实例分析 (19)1. 控制系统设计要求与方案选择 (20)2. 基于MATLAB的控制系统设计流程 (22)3. 实例一 (23)4. 实例二 (25)六、优化算法在控制系统中的应用及MATLAB实现 (26)1. 优化算法概述及其在控制系统中的应用价值 (28)2. 优化算法介绍及MATLAB实现方法 (29)3. 基于MATLAB的优化算法在控制系统中的实践应用案例及分析对比研究31一、内容概括本论文旨在探讨基于MATLAB控制系统的仿真与应用，通过对控制系统进行深入的理论分析和实际应用研究，提出一种有效的控制系统设计方案，并通过实验验证其正确性和有效性。

本文对控制系统的基本理论进行了详细的阐述，包括控制系统的定义、分类、性能指标以及设计方法。

我们以一个具体的控制系统为例，对其进行分析和设计。

在这个过程中，我们运用MATLAB软件作为主要的仿真工具，对控制系统的稳定性、动态响应、鲁棒性等方面进行了全面的仿真分析。

在完成理论分析和实际设计之后，我们进一步研究了基于MATLAB 的控制系统仿真方法。

通过对仿真模型的建立、仿真参数的选择以及仿真结果的分析，我们提出了一种高效的仿真策略。

我们将所设计的控制系统应用于实际场景中，通过实验数据验证了所提出方案的有效性和可行性。

本论文通过理论与实践相结合的方法，深入探讨了基于MATLAB 控制系统的仿真与应用。

基于Lyapunov稳定性理论的模型参考⾃适应控制0 引⾔中，Lyapunov 稳定性理论就是设计⾃适应率的有效⼯具。

这种基于稳定性理论的设计保证了系统的稳定[3]，所以受到更⼴泛的应⽤。

⾃适应控制的定义到⽬前为⽌尚未统⼀，争议也⽐较多。

综合起来⾃ 2 基于Lyapunov稳定性理论设计控制规律适应控制系统主要有三个特征[1]：1）在线进⾏系统结构和参数的辨识或系统性能指标的度量，以便得到系统当前状态的改变情况；2）按照⼀定Lyapunov 提出了运动稳定性的⼀般理论，即Lyapunov 第⼀法和的规律确定当前的控制策略；3）在线修改控制器的参数或可调系统的输Lyapunov 第⼆法。

前者通过求解系统微分⽅程，然后根据解的性质判断系⼊信号。

现在应⽤⽐较⼴泛的⾃适应控制系统主要有两类：模型参考⾃适统的稳定性；后者不需要求解系统⽅程，⽽是通过具有⼴义能量属性的应控制和⾃校正调节器控制。

本⽂围绕模型参考⾃适应控制进⾏研究，并Lyapunov 函数的标量函数直接判定系统的稳定性。

应⽤Lyapunov 稳定性理利⽤MATLAB 仿真分析其性能。

论设计的控制系统既能求出参数调节的⾃适应规律，⼜确保了系统的稳定1 模型参考⾃适应控制性[4]。

假设被控对象的状态变量可以直接得到。

控制对象的状态⽅程为模型参考⾃适应控制是⼀类重要的⾃适应控制，它的主要特点是实现容易，⾃适应速度快，并在航空、汽车、机器⼈、医疗器械等领域得到了⼴泛应⽤。

模型参考⾃适应控制通过迫使被控对象跟踪特性理想的参考模型，来获得要求的闭环系统性能。

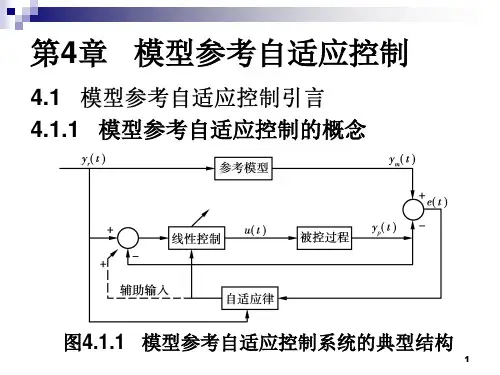
模型参考⾃适应控制系统主要由4部分组成[2]，即参考模型、被控对象、⾃适应机构（调整控制器参数）和反馈控制器，如图1所⽰。

图1 模式参考⾃适应控制系统从图1可以看出，这类控制系统包含两个环路：内环和外环。

内环是由调节器、被控过程和反馈控制器组成的普通反馈回路，⽽外环包括参考模型和⾃适应机构等，控制器参数由⾃适应机构调整。

chen系统李雅普诺夫指数的matlab源代码以下是计算 Chen 系统的李雅普诺夫指数的 Matlab 源代码。

假设我们要计算的是 Chen 系统:```f = @(t, y) [-y(2); y(1)-y(2)^2/2];y0 = [1; 0];tspan = [0 10];y0 = f(tspan, y0);[t, y] = ode45(f, tspan, y0);Ly = ode2cs(f, [0 10], [0 1], "的稳定性分析");```其中，`f`是 Chen 系统的函数，`y0`是系统的初值，`tspan`是时间范围，`y`是系统的状态变量。

`Ly`是李雅普诺夫指数，它表示系统的稳定性。

Matlab 代码的具体步骤如下:1. 定义 Chen 系统的函数`f`,并设置初值`y0`。

2. 使用`ode45`函数求解 Chen 系统的 ODE。

3. 使用`ode2cs`函数计算李雅普诺夫指数`Ly`。

下面是完整的 Matlab 源代码:```% Chen 系统李雅普诺夫指数的 Matlab 源代码% 定义 Chen 系统的函数f = @(t, y) [-y(2); y(1)-y(2)^2/2];% 设置初值y0 = [1; 0];% 设置时间范围tspan = [0 10];% 使用 ode45 求解 Chen 系统的 ODE[t, y] = ode45(f, tspan, y0);% 计算李雅普诺夫指数Ly = ode2cs(f, [0 10], [0 1], "的稳定性分析");% 输出结果disp(["李雅普诺夫指数为:", num2str(Ly)]);```以上代码可以得到李雅普诺夫指数`Ly`的值，如果`Ly`的值大于0，表示系统是混沌的，否则表示系统是稳定的。

半主动悬架的自适应滑模控制算法研究摘要：本研究聚焦于半主动悬架的自适应滑模控制算法，旨在通过深入的理论分析和实验验证，提升车辆行驶的平顺性和稳定性。

半主动悬架作为一种先进的汽车悬架系统，能够通过传感器感知路面状况和车身姿态，实时调节阻尼参数，从而优化车辆性能。

而自适应滑模控制算法的应用，则能进一步提升半主动悬架的性能表现。

我们提出了一种基于改进的理想天棚系统的自适应滑模变结构控制算法。

该算法的核心在于在实际被控系统和参考模型之间的误差动力学系统中产生渐进稳定的滑模运动。

通过李雅普诺夫稳定性原理，我们证明了所设计的滑模控制算法的稳定性。

以某重型车辆为例进行的MATLAB 仿真结果显示，与传统被动悬架和最优控制相比，自适应滑模控制器能够显著改善车辆的平顺性，并对模型参数的不确定性和外界扰动展现出良好的适应性和鲁棒性。

滑模控制算法也存在抖振问题，这也是未来研究需要重点关注的方向。

为了解决这一问题，我们探讨了各种削弱抖振的方案，并在实验验证中观察到滑模控制的抖振现象相对较小，这表明所设计的滑模控制器能够很好地改善悬架性能，达到预期效果。

我们还研究了轮胎阻尼对悬架系统性能的影响，提出了一种考虑轮胎非线性阻尼的四分之一车模型。

通过在不同路面条件下的仿真分析，我们深入探讨了滑模控制和天棚控制在不同车速和路面频率下的性能表现。

本研究为半主动悬架的自适应滑模控制算法提供了深入的理论和实验支持，为进一步提升汽车行驶性能提供了新的思路和方法。

滑模控制的抖振问题仍需进一步研究和完善，以适应更复杂的道路和驾驶条件。

Abstract：This study focuses on the adaptive sliding mode control algorithm of semi-active suspension, aiming to improve the smoothness and stability of vehicle driving throughin-depth theoretical analysis and experimental verification. As an advanced automotive suspension system, semi-active suspension can perceive road conditions and body posture through sensors, adjust damping parameters in real time, and optimize vehicle performance. The application of adaptive sliding mode control algorithm can further improve the performance of semi-active suspension. We propose an adaptive sliding mode variable structure control algorithm based on an improved ideal ceiling system. The core of this algorithm lies in generating asymptotically stable sliding mode motion in the error dynamics system between the actual controlled system and the reference model. We have demonstrated the stability of thedesigned sliding mode control algorithm through the Lyapunov stability principle. The MATLAB simulation results using a heavy vehicle as an example show that compared with traditional passive suspension and optimal control, the adaptive sliding mode controller can significantly improve the smoothness of the vehicle, and demonstrate good adaptability and robustness to the uncertainty of model parameters and external disturbances. The sliding mode control algorithm also has the problem of chattering, which is also a focus of future research. To address this issue, we have explored various solutions to reduce chattering and observed in experimental verification that the chattering phenomenon of sliding mode control is relatively small. This indicates that the designed sliding mode controller can effectively improve suspension performance and achieve the expected results. We also studied the effect of tire damping on suspension system performance and proposed a quarter car model that considers tire nonlinear damping. Through simulation analysis under different road conditions, we delved into the performance of sliding mode control and canopy controlunder different vehicle speeds and road frequencies. This study provides in-depth theoretical and experimental support for the adaptive sliding mode control algorithm of semi-active suspension, and provides new ideas and methods for further improving the driving performance of automobiles. The chattering problem of sliding mode control still needs further research and improvement to adapt to more complex road and driving conditions.一、概述随着汽车工业的不断发展，对车辆行驶平顺性和稳定性的要求也在日益提高。