24.2 圆的切线 课件2 (北京课改版九年级下册)

生死教会她锐利果敢。所以她说，那一刻，没有一个母亲，会如苏珊般高贵沉着。 九天九夜的追捕，孩子们找到了。不在暗夜不在森林，而沉在冰冷的湖底。苏珊，终于向警方自首，的确是她，因为一点情欲的贪念，亲手杀了自己的孩子。
1994年的事了。偶尔在一本书里，读到前因后果，和那陌生女子的信。我低一低头，其实并没有泪。我想我懂。 我尚不及为人母，也不曾遭逢死亡，我却曾站在高处林下，看着爱人轻快远去，仿佛有鹳雀在他鞋底翻飞，他是急着赶另一个女子的约会吧?真相凄厉地直逼眼前。不是不知道，在泪落之前应该说再见，我却做不到。因为我爱他。
2 设圆的方程为x2+(y-1)2=1,求该圆的 斜率为1的切线方程. x-y+1± 2 =0
例 3 当k为何值时，直线y=kx与圆(x-1)2+(y-2)2=1
相交，相切，相离？ 解： 法一：代数法：方程组有无实数解。
法二：圆心为（1，2），到直线y=kx即
kx-y=0的距离为 d= k-2 k2+1
我开始虚伪，听着谎言却装做一无所知；我学会窥探，四处打听如蛇之祟行，而十分看轻自己； 我的故事越编越好，好莱坞金牌编剧也没这般丰富多采，只为让他多留一分钟。
最后，我打他一巴掌。干脆痛快，出手的瞬间，像那位绝望的母亲，远远掷出她的高跟鞋。掷中没有？并不重要。 有多爱，就有多不舍；有多温柔，就有多暴烈，爱得唇边有血，眼中有泪，胸口有纠缠的爱与恨，爱到如连体婴般骨肉相连。割爱，就一定不可能如拈去一片花叶般轻松微笑。 明知留不住，收不下，却不能自控我颠倒狂乱的脚步。那一遭，我是夜深街上，追逐汽车的女子。而我无声的哭泣，他没有听见。快乐是人类社会众望所归的最高境界。所谓君子之交谈如水。一个把名缰利锁看得太重的人。注定是不快乐的。快乐就是看淡尘世的物欲、烦恼，不慕荣利。假如你喜欢武侠小说，你没有必要愧对红楼梦； 假如你喜欢的人突然销声匿迹，你没有必要寻死觅活地断言他一定洒脱地离去；假如你的朋友不幸，你没有必要怨天尤人；假如你认为张曼玉艳美绝俗，你没有必要眼馋肚饱虐待老婆；假如你已经身心交病，那就去教堂忏悔，没有必要仇视别人的平庸；坦然面对心融神会，快乐就在你心里。我怜悯一个有点荣誉的人，就旁若无人而因此失 去快乐的人。能把名利得失置之度外，而凡事都能以诚相待的人一生将是快乐的。我们应从平谈的生活中去提炼体会，如：赤城待人的那种快乐。低待遇下一如既往工作的快乐，助人为乐一介不取的快乐，一片至诚去感化恶人的快乐，热心被人误解依然如故的快乐，信实可靠的服务态度为目的的快乐，尽责任吃苦耐劳的快乐，因为这些 “快乐”能保持住人内心的快乐，使人的容貌永远那么牵挂，一句亲切的问候。甚至一个关切的眼神，快乐无处不有，唯有胸襟开阔的人，才能体会到。形单影只的人仍然可以享受着闲情逸致的快乐。乐山乐水各不相同。爱静的人可以看书、听音乐、上网、写作、画画、搜集各种收藏品。爱动的人则不妨练习舞蹈、慢跑、爬山、游泳。看 电影、上健身房。做编织、陶艺。练瑜枷、潜心发明、闭门创作，摄影、观鸟，我们仍然兴复不浅，乐不可支。人生苦短，岁月如流，乐天知命，为什么不乐乐陶陶的。为什么要疾首蹙额，为眼前一时的顿挫心胆俱碎？为什么要对那些你看不惯的人和事心烦率乱？岂不知我们都是尘世间相映成趣的战友。人世一切冤天屈地，无妄之灾，荣 华富贵，香娇玉嫩……都将随身亡命殒。而人生长着百年，短则数十寒暑，又有何值得耀武扬威的，不过是烟云过眼矣？人生如月，月满则亏，凡事岂能尽人意，但求于心无愧。无愧我心，则恩同再造，那些得失又算不了甚么。世界上没有完美无缺得事物。奉劝多愁善感的朋友。饮醇自醉，快乐起来吧！芸芸众生，绿水青山，名胜古迹，

2. 圆心为 O 的两个同心圆，半径分别为 1 和 2，
若OP= 3 ，则点 P 在（ D ）
A.大圆内
B.小圆内
o
C.小圆外
D.大圆内，小圆外
要点归纳
P d O
r
Od P
r
P
dO r
P O
Rr
点 P 在⊙O 内 d<r 点 P 在⊙O上 d=r
点 P 在 ⊙O 外 d>r 点 P 在圆环内 r＜d＜R
劣弧：AF, AD,AC,AE.
F
O
E
(
( (( ((
(
((
优弧：AFE, AFC,AED,AEF. (2) 请写出以点 A 为端点的弦及直径. A
C
弦 AF，AB，AC.其中弦 AB 又是直径. (3) 请任选一条弦，写出这条弦所对的弧.
答案不唯一，如：弦 AF，它所对的弧是 AF.
知识要点
1. 根据圆的定义，“圆”指的是“圆周”,而不是“圆面”.
r rO· r
A
有点组成的图形．定点就是圆心，定长就是 C r r E
半径，以点 O 为圆心的圆记作 ⊙O，读作
“圆 O ”.
有关概念
固定的端点 O 叫做圆心，线段 OA 叫做半径，一
般用 r 表示．
确定一个圆的要素 一是圆心，确定其位置；二是半径，确定其大小．
同心圆 圆心相同，半径不同
等圆
能够重合 的两个圆 叫做等圆.
系？
P
d O
r
Od
r
P
Pd O r
点 P 在 ⊙O 内 点 P 在⊙O上
d＜ r d =r
点 P 在⊙O 外
d ＞r
练一练：

∠DAB
D
C
A
O
B
例题选讲
例：AB是⊙O的弦,C是⊙O外一点,BC是⊙O的 切线,AB交过C点的直径于点D,OA⊥CD,试判断 △BCD的形状,并说明你的理由.
A
D O
C
B
切线的判定方法 有三种： ①直线与圆有唯一公共点； ②直线到圆心的距离等于该圆的半径； ③切线的判定定理．
切线的性质： 定理：圆的切线垂直于过切点的半径.
探索新知
请大家自学课本P97“思考”以上的内容，请大家再 思考：在⊙O中，直线L过⊙O的半径OA的外端点A，且 L⊥OA于A点，则圆心O到直线L的距离是多少？直线L 和⊙O有什么位置关系？
探索新知
切线的判定定理：
经过半径的外端并且垂直于这条半径的 直线是圆的切线。
已知一个圆和圆上的一个点， 如何过这个点画出圆的切线？ 自己动手试一试！
2.切线的判定方法：
（１）定义
直线和圆有唯一公共点时，叫做直线和 圆相切。
( 2 ) d=r
直线与圆相切
（３）切线的判定定理.
已知直线过圆上一点： (连半径，证垂直）
不明确直线是否过圆上一点： (作垂直，证半径）
探索新知
反过来,如么
半径OA与直线L是不 是一定垂直呢?
九年级数学 教学课件
商城思源实验学校 杨成超
回忆旧知， 引入新课：
1、认真回忆如何判断直线和圆的位置关系？
（1）直观观察； （2）直线和圆公共点个数； （3）数量关系：d与r的大小关系。
2、请大家根据上述方法分析，直线和圆相切的判断 方法：
（1）直线和圆公共点个数：只有一个公共点时。 （2）数量关系： d=r 。 3、这节课我们继续探索新的判断直线和圆相切的方 法。

知2－讲
导引：(1)已知BC是⊙O的直径，可连接CD，构造直径 所对的圆周角，结合AD＝DB，可得AC＝BC；
(2)要证DE是⊙O的切线，而点D在圆上，可联想 到连接OD，设法证DE⊥OD即可．
解：(1) 连接CD，如图. ∵BC是⊙O的直径， ∴∠BDC＝90°，即CD⊥AB， ∵AD＝DB， ∴AC＝BC＝2OC＝10.
知1－练
6 如图，AB是⊙O的直径，线段BC与⊙O的交点D 是BC的中点，DE⊥AC于点E，连接AD，则下列 结论中正确的个数是(D )
①AD⊥BC；②∠EDA＝∠B；
③OA＝ 1 AC；④DE是⊙O的切线．
2
A．1
B．2
C．3
D．4
知识点 2 切线的性质和判定的应用
知2－导
例2 [中考·湖州]如图，已知BC是⊙O的直径，AC切⊙O 于点C，AB交⊙O于点D，E为AC的中点，连接DE. (1)若AD＝DB，OC＝5， 求切线AC的长； (2)求证：DE是⊙O的切线．
B．3个
C．2个
D．1个
1 知识小结
切
线
↗的
判
圆
定
的
切
线
↘切 线 的
性
质
↗ → ↘ ↗ → ↘
定义法 数量法d=r 判定定理
切线和圆只有一个公共点 圆心到切线的距离等于半径 圆的切线垂直于过切点的半径
2 易错小结
如图，点O为∠MPN的平分线上一点，以点O为圆心 的⊙O与PN相切于点A. 求证：PM为⊙O的切线．
（来自《典中点》）
知识点 2 切线长定理的应用
知2－讲
例2 如图，PA，PB是⊙O的切线，切点分别为A，B， BC为⊙O的直径，连接AB，AC，OP. 求证：(1)∠APB＝2∠ABC； (2)AC∥OP.

通过圆上一点作切线
总结词
通过圆上一点作切线需要利用半径垂直于切线的性质。
详细描述
选取圆上任意一点，然后通过这一点作一条直线与圆相切，即为切线。这种方法 需要利用圆的性质，即半径垂直于切线。
通过圆外一点作切线
总结词
通过圆外一点作切线需要利用垂径定 理和切线的性质。
详细描述
选取圆外任意一点，然后通过这一点 作一条直线与圆相切，即为切线。这 种方法需要利用垂径定理和切线的性 质，即半径与切线垂直且半径长度等 于圆心到切点的距离。
判定方法三
利用圆的性质，通过观察 圆心到直线的距离是否等 于半径来判断是否为切线 。
02 圆的切线的性质定理
切线与半径垂直
切线与经过切点的半径垂直， 这是切线的基本性质。
在几何学中，这一性质用于证 明切线的其他性质和定理。
在实际应用中，这一性质可用 于确定某直线是否为圆的切线 。
切线长定理
切线长定理：从圆外一点引圆的两条切线，它们的切线长相等。 这一性质在几何作图和证明中非常有用，特别是在解决与圆和切线相关的问题时。
05 圆的切线的相关定理和推论
切线与半径之间的夹角定理
总结词
切线与半径之间的夹角定理描述了切线与半径之间的角度关系。
详细描述
切线与半径之间的夹角是直角，即切线与半径垂直。这个定理是圆的基本性质之一，是证明其他切线定理的基础 。
切线长定理的推论
总结词
切线长定理的推论给出了切线长度与半径之间的关系。
圆的切线ppt课件
目录
Contents
• 圆的切线的基本概念 • 圆的切线的性质定理 • 圆的切线的应用 • 圆的切线的作法 • 圆的切线的相关定理和推论
01 圆的切线的基本概念

l
注意：实际证明过程中，通常不采用第一种
方法;方法2从“量化”的角度说明圆的切线的
判定方法。
-
5
请在⊙O上任意取一点A，连接OA， 过点A作直线l⊥OA。思考：
（1） 圆心O到直线l的距离和
圆的半径有什么数量关系?
（2） 二者位置有什么关系？
为什么？
l
（3） 由此你发现了什么？ -
O
A
6
(1)直线l经过半径OA的外端点A；
1、知识：切线的判定定理．着重分析了定理成 立的条件，在应用定理时，注重两个条件缺一不 可． 2、判定一条直线是圆的切线的三种方法说明： 其中(2)和(3)本质相同，只是表达形式不同．解 题时，灵活选用其中之一．
-
22
思考？如图：如果L是⊙O 的切线,切点为A,那么 半径OA与直线L是不 是一定垂直呢? 一定垂直
直线l
与圆有唯一公共点 与圆心的距离等于圆的半径 经过半径外端且垂直这条半径
l是圆的切线 l是圆的切线 l是圆的切线
2. 常用的添辅助线方法？ ⑴直线与圆的公共点已知时，作出过公共点的半径，
再证半径垂直于该直线。（连半径，证垂直） ⑵直线与圆的公共点不确定时，过圆心作直线的垂
线段，再证明这条垂线段等于圆的半径。（作垂直， 证半径）
l
-
O r A
9
判断：
(1)过半径的外端的直线是圆的切线（×） (2)与半径垂直的的直线是圆的切线（×）
(3)过半径的端点与半径垂直的直线是圆的
切线（×）
O l
r
A
O r
l
A
-
O l
r
A
10
判定直线与圆相切有哪些方法？

能够重合的两个圆叫做等圆，等圆的半径相等. 在同圆或者等圆中，能够互相重合的弧叫做等弧.
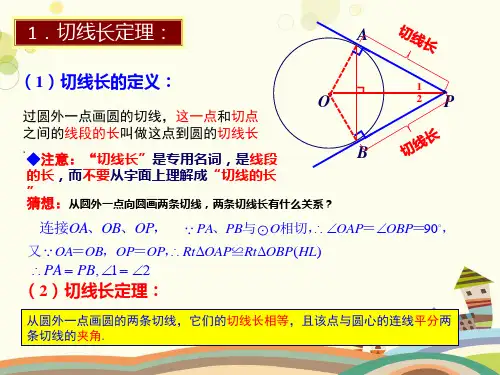
例题分析：
例1 已知：如图24-17，AB,CD为⊙O的直径. 求证：AD//CB. 证明: 连接AC,DB.
∵ AB,CD为⊙O的直径
∴ OA=OB， OC=OD ∴ 四边形ABCD为平行四边形.
图 24-17
同圆或等圆中， 两个圆心角、 两条弧、两条 弦中有一组量 相等，它们所 对应的其余各 组量也相等．
性质
n°弧
∵把圆心角等分成360份,则每一份的
圆心角是1º.同时整个圆也被分成了360
n°
份. 则每一份这样的弧叫做1º的弧. 这样,1º的圆心角对着1º的弧,
1°
1°弧
1º的弧对着1º的圆心角.
n º的圆心角对着nº的弧,
n º的弧对着nº的圆心角. 性质:弧的度数和它所对圆心角的度数相等.
例4 如图，在⊙O中，AB = AC ，∠ACB=60°，
求证:∠AOB=∠BOC=∠AOC.
A
证明：∵ AB = AC
∴ AB=AC, △ABC 等腰三角形．
O
又∠ACB=60°，
B
C
∴ △ABC是等边三角形，AB=BC=CA.
(2)圆是由圆心和半径确定的,圆心确定圆的位置,半径 确定圆的大小).
交流：
点与圆的位置关系
平面上有一个圆，这个平面上的点，除了在圆上外， 与圆还有几种位置关系，这些关系根据什么来确定？
（1）若点A在⊙O上 （2）若点A在⊙O 内 （3）若点A在⊙O外
OA r
OA r
OA r
符号 读作等价于.它表示从符号的 左边可以推出右边；同时从符号的右 边也可以推出左边.

方法总结：图形中求三角形外接圆的面积时，关键是 确定外接圆的直径(或半径)长度．
当堂练习
1.判断： 〔1〕经过三点一定可以作圆 〔 ×〕 〔2〕三角形的外心就是这个三角形两边垂直平分线的
交点 〔 √ 〕 〔3〕三角形的外心到三边的距离相等 〔×〕 〔4〕等腰三角形的外心一定在这个三角形内 〔 ×〕
O
E
B
PC
3.△ABC的内切圆⊙O与三边分别切于D、E、F三点，如 图，AF=3,BD+CE=12,那么△ABC的周长是 30 .
A
F
E
O
BD
C
第4题
A
拓展提升：
直角三角形的两直角边分别是3cm ,4cm,试问：
〔1〕它的外接圆半径是 5 cm;内切圆半径
D
F O·
是 1 cm？
〔2〕假设移动点O的位置，使⊙O保持与△ABC的 C E
填一填：
三角形三边
中垂线的交
点
B
三角形三条 角平分线的 交点
B
A
1.OA=OB=OC
2.外心不一定
O
在三角形的内 部．
A
1.到三边的距离相 等；
2.OA、OB、OC分
别平分∠BAC、
O
∠ABC、∠ACB; 3.内心在三角形内
C 部．
例3 △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、
E、F，且AB=13cm，BC=14cm，CA=9cm，求AF、BD、CE
A．第①块 C．第③块
B．第②块 D．第④块
二 三角形的外接圆及外心
试一试： △ABC，用直尺与圆规作出过A、B、C
三点的圆.
A
O C
B

r内＝
5
12 2
13＝
4 2
＝2
即：它的内切圆半径为2
《导学案》P100 例2
（1）目标锁定：证1＝2
证： E是ABC的内心
3
EA、EB分别为CAB、CBA的角平分线
12
又 CA＝CB，CAB＝CBA
1＝2， AE＝BE
（2）锁定目标：证CAB∽DEB
证：连接BD 3＝1 2＝21＝CAB
又 C＝D，CAB∽DEB
1．切线长定理：
A
（1）切线长的定义：
┓
O
过圆外一点画圆的切线，这一点和切点
之间的线段的长叫做这点到圆的切线长
.◆注意：“切线长”是专用名词，是线段
B
的长，而不要从字面上理解成“切线的长
”猜想：从圆外一点向圆画两条切线，两条切线长有什么关系？
1
2P
连接OA、OB、OP， PA、PB与 O相切，OAP＝OBP＝90 ，
E F
C
AB＝AC DB＝DE EF＝CF
结论：
ADF的周长＝AB AC＝2AB
《导学案》P93 例1 10
57°
114° 57° 66°
57°或123°
《导学案》P95 第4题
219° ∠PAB＝（180°-102°）/2＝78°/2＝39°
180°+39°＝219°
39° 102° 39°
又 BE＝AE， AB AE AC DE
AB BE AC DE
《导学案》P100 例3
（1）证：连接BI， I是ABC的内心
1＝2，3＝4 6＝2 3，6＝1 4
又 1＝5，6＝4 5＝DBI DB＝DI
（2） 5＝1＝2，D＝D

•
13、生气是拿别人做错的事来惩罚自 己。2021/8/212021/8/212021/8/212021/8/218/21/2021
•
14、抱最大的希望，作最大的努力。2021年8月21日 星期六 2021/8/212021/8/212021/8/21
•
15、一个人炫耀什么，说明他内心缺 少什么 。。2021年8月 2021/8/212021/8/212021/8/218/21/2021
•
12、人乱于心，不宽余请。***Saturday, August 21, 2021
•
13、生气是拿别人做错的事来惩罚自 己。21.8.2121.8.21**August 21, 2021
•
14、抱最大的希望，作最大的努力。2021年8月21日 星期六 **21.8.21
•
15、一个人炫耀什么，说明他内心缺 少什么 。。2021年8月 *21.8.21*August 21, 2021
谢谢大家
2021/7/25
21
14
直线和圆 的位置关
系
图形
公共点个 数
公共点名 称
直线名称 2021/7/25
总结梳理 内化目标
相交
d Or l AB
2个 交点 割线
d＜r
相切
d Or A
l
1个
切点
切线
d=r
相离
O r
d l
没有
d－＞r
－
15
达标检测 反思目标
C A
2021/7/25
16
2021/7/25
相交
d>3cm d=3cm 0≤d<3cm
•
10、低头要有勇气，抬头要有低气。* **8/21/2021 12:1.21**Aug-2121- Aug-21

kCA kAM 1
2019/10/18
可编辑
6
2019/10/18
7
三、经过圆外一点，求圆的切线方程
已知圆C的方程为 (x a)2 ( y b)2 r，2
求经过圆外一点 M (x0 , y0 ) 的切线l方程。
分析：1.特殊情况 2.一般情况： 经过圆外一点可以作两条切线 思路二：求切线斜率
例1：已知圆C的方程为(x 1)2 ( y ，1)2 5
求经过圆上一点 M (2的,3)切线方程。
2019/10/18
可编辑
4
二、经过圆上一点，求圆的切线方程
例2：已知圆C的方程为 x2 y2 ， r求2 经过圆上
一点 M的(切x0线, y方0 ) 程。
练习：已知圆C的方程为 x2 y2 10 ， 求经过点P（1,3）的圆的切线方程。
9
四、总结
2019/10/18
可编辑
10
四、练习
1.求圆C x2 y2 4x 0 在点 P(1, 3) 处的切线方程。
2.已知圆C的方程为 x2 ( y 2)2 1，求经过原点 的切线方程。
3.已知圆C的方程为 x2 y2 2 y 0，求该圆的斜 率为1的切线方程。
一、复习讨论
1、圆的切线有何性质？
圆心与切点间的距离等于半径
圆心与切点的连线与切线垂直
2、怎样判断一条直线和圆是否相切？
d r
0
3、两条直线垂直，它们的斜率有什么关系？
k1 k2 1
4、直线的点斜式方程是怎样的？
y y0 k(x x0 )
2019/10/18
可编辑
2

?
代表阶级利益：地主阶级
要
宣传手段：前者著书，后者实践办厂；
实践效果 结果 作用
洋务运动的影响
1、引进西方先进科技和工具 2、培养科技人员和技术工人 3、刺激民族资本主义发展 4、一定程度抵制外国经济扩张 5、在改革封建教育制度上打开了缺口
失败标志：甲午中日战争的失败 失败原因：单纯引进西方先进技术和设备，而
② 梁启超
A. 代表作：《变法通议》 B. 主张：
抨击 ……2 宣传 ……3 今日策中国者，必曰兴民权。 （1873——1929） 变法之本，在育人才，人才之兴，在开学 校，学校之立，在变科举，而一切要其大 成，在变官制。
3、维新思想的传播 ——与封建顽固势力的论战
① 原因：维新思想传播遭到封建顽固势力反对
实践 掀起洋务运动 影响
掀起维新变法 思想启蒙
思考： 维新变法思想的性质、目的、失败原因
求证：直线AB是⊙O的切线. O
证明：连结OC(如图)
∵ OA＝OB,CA＝CB
A
C
B
∴ OC是等腰三角形OAB底边AB上的中线
∴ AB⊥OC
∵ OC是⊙O的半径
∴ AB是⊙O的切线.
〖例2〗
已知：O为∠BAC平分线上一点，OD⊥AB于D,
以O为圆心，OD为半径作⊙O.
求证：⊙O与AC相切.
证明：过O作OE⊥AC于E
用判定O定理时，要注O意直线须具备O以
l下两个r 条件,缺一不可r : l
l r
(1)直线经过半径的外端;
(2)A直线与这条半A径垂直。 A
1.已知⊙A的直径为6，点A的坐标
为（-3，-4），则⊙A与x 轴的位
置关系是_相__离__,⊙A与y 轴的位置

[解题过程] (1)证明：依据题意，得 a＋b＝c＋4，ab＝4(c＋2)， 则 a2＋b2＝(a＋b)2－2ab ＝(c＋4)2－2×4(c＋2)＝c2， 所以△ABC 是直角三角形．
(2)∵∠C＝90°，tan A＝ab＝34， ∴不妨设 a＝3k，b＝4k，则 c＝5k(k>0)， 代入 a＋b＝c＋4，得 k＝2. ∴a＝6，b＝8，c＝10. 连接 OE，得 BC∥OE. ∴OBCE＝AAOB，即O6E＝10－10OE.解得 OE＝145. 在 Rt△AOE 中，tan A＝OAEE＝34，∴AE＝5.
[规律方法] 用切线的性质定理求解线段的长度时，应注 意哪些问题？
(1)如果已知三边的一元二次方程，可利用韦达定理建立起 三角形的三边之间的关系；
(2)在应用切线的性质定理及其推论进行几何证明和求解 时，如果已知切点，则连接圆心和切点构成垂直是一种常用的 方法．
(江苏高考)AB是圆O的直径，D为圆O上一点， 过D作圆O的切线交AB延长线于点C，若DA＝DC，求证：AB
[思路点拨]
[解题过程] 如图所示，连接OA、OB、OC．
∵PA和PB分别切⊙O于点A和B， ∴∠PAO＝∠PBO＝90°. ∴∠AOB＋∠APB＝180°. ∴∠AOB＝180°－∠APB＝140°. ∵DC切⊙O于点C，∴∠OCD＝90°.
又∵∠PAO＝90°， 在 Rt△CDO 与 Rt△ADO 中， 有 OD＝DO，CO＝AO， ∴△CDO≌△ADO.
∴∠COD＝∠AOD＝12∠COA． 同理可证，∠COE＝∠BOE＝12∠COB．
∴∠DOE＝12(∠COA＋∠COB)＝12×140°＝70°.
[规律方法] (1)如何利用切线性质定理及推论求解有关角 的问题？

∠P= 50 °，点C是⊙O上异于A、B的点，则
∠ACB= 65 °或115 °.
P
O
B
五、当堂达标检测
6.△ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E，F，且
AB=9cm，BC=14cm，CA=13cm，求AF，BD，CE的长.
解：设AF=x,则AE=x
∴CD=CE=AC-AE=13-x，
A
D
P
O
C
E
B
二、自主合作，探究新知
又∵DC、DA是☉O的两条切线，点C、A是切点，
∴DC=DA.同理可得CE=EB.
l△PDE=PD+DE+PE=PD+DC+CE+PE=PA+PB=14.
∵OA=OC，OD=OD，
∴△AOD≌△COD，

∴∠DOC=∠DOA= ∠AOC.

P

同理可得∠COE= ∠COB.
7.如图，在△ABC 中，∠ABC=50º，∠ACB=75º,点O是△ ABC的内心，
求∠BOC的度数.
解：∵点O是△ABC 的内心,
∴∠OBC
∠OCB

= ∠ABC


= ∠ACB


= ×50º=

25º,

= ×75º=37.5º.

在△OBC 中，∠BOC =180º- ∠OBC - ∠OCB
=180º- 25º- 37.5º= 117.5º.
四、课堂小结
切线长
切线长定理
切线长定理
经过圆外一点作圆的切线，这点和切
点之间的线段的长叫作切线长．
过圆外一点画圆的两条切线，它们的

C 共点A是⊙O的 a切点 。
满足什么条件的直线是圆的切线呢？
精品
新知讲解
探究
如图，OA是⊙O 的半径， 经过 OA 的外端点 A， 作一条直线l⊥
OA
，
圆心
O
到直线
l
的距离是多少？
直线
l
和⊙O
有怎样的位
D
置关系？
A
l
A
∟
a
O
精品
新知讲解
1. 圆心O到直线 l 的距离等于半径OA。
2. 由圆的切线定义可知直线 l 与圆O相切。
∴ 直线 BC 是⊙O 的切线．
精品
新知讲解
三、判定直线与圆相切的方法
①定义法：直线与圆有唯一公共点；
D
A
②数量法：直线到圆心的距离等于该圆的半径；
a
③切线的判定定理：经过半径的外端并且垂直这条半径的直 线是圆的切线。
精品
新知讲解
已知：直线AB经过⊙O上的点C，并且OA=OB，CA=CB。
求证：直线AB是⊙O的切线。
D
A
几何语言：
O.
∵直线 l 是⊙O 的切线，点 A 为切点，
a
l
∴OA ⊥ l
A
精品
新知讲解
因为经过一点只有一条直线与已知直线垂直，所
以经过圆心垂直于切线的直线一定过切点；反之，
过切点且垂直于切线的直线也一定过圆心。因此 l
我们可以得到两个推论。
A
O.
D
A
切线的性质定理的推论１:经过圆心且垂直于a 切线的直线必经
Al
Oቤተ መጻሕፍቲ ባይዱ
D
直线是圆的切线A
aA l

∴∠1＝∠3，∴OD∥AE.
∵DE⊥AE，∴DE⊥OD， 即 DE 是⊙O 的切线．
(2)过 D 作 DG⊥AB， ∵∠1＝∠2，∴DG＝DE＝3. 在 Rt△ODG 中，OG＝ 52－32＝4， ∴AG＝4＋5＝9.
∵DG⊥AB，FB⊥AB，∴DG∥FB.
∴△ADG∽△AFB，∴DBFG＝AAGB. ∴B3F＝190，∴BF＝130.
【自主解答】 (1)如图所示，连接 BC. ∵CD 为⊙O 的切线， ∴OC⊥CD. 又 AD⊥CD，
∴OC∥AD.
(2)∵AC 平分∠DAB， ∴∠DAC＝∠CAB. ∵AB 为⊙O 的直径，∴∠ACB＝90°. 又 AD⊥CD，∴∠ADC＝90°， ∴△ADC∽△ACB. ∴AADC＝AACB，∴AC2＝AD·AB. ∵AD＝2，AC＝ 5，∴AB＝52.
1．“以圆的两条平行切线的切点为端点的线段是圆的 直径”这句话对吗？为什么？
【提示】 正确．如图 AB、CD 分别切⊙O 于 E、F， 连接 EO 并延长交 CD 于 F′，∵AB 是⊙O 的切线，∴OE
⊥AB.∵AB∥CD，∴OF′⊥CD，∴F′为切点，∴F′与 F
重合，即 EF 是⊙O 的直径．
圆的切线的性质及判定定理
1．切线的性质定理及推论
(1)性质定理：圆的切线垂直于经过 切点的半径．
如图 2－3－1，已知 AB 切⊙O 于点 A，则 OA⊥AB.
(2)推论 1：经过圆心且 垂直于切线的直线 必经过切点． (3)推论 2：经过切点且 垂直于切线的直线 必经过圆心．
图 2－3－1
2．切线的判定定理 经过半径的 外端 并且 垂直于 这条半径的直线是圆的 切线．
如图 2－3－2 所示，已知
AB 是⊙O 的直径，直线 CD 与⊙O 相切 于点 C，AC 平分∠DAB，AD⊥CD.