仁华思维导引解析7讲:乘除法填空格(三年级)
- 格式:doc
- 大小:395.00 KB
- 文档页数:7


思维数学-乘除法填空格讲解(讲义)教案一、教学目标:1.知识目标(1)掌握乘法、除法的概念(2)掌握算术各种乘法、除法的口诀(3)通过填空格等形式,运用乘除法解决实际问题2.能力目标(1)通过思考及探究,让学生掌握乘除法的原理(2)培养学生逻辑思维及解决问题的能力3.情感目标(1)激发学生学习数学的兴趣(2)培养学生对数学的认知及探究精神二、教学内容:乘除法填空格讲解三、教学重点、难点:1.重点:掌握乘除法的概念及口诀2.难点:通过填空格的方式,运用乘除法解决实际问题四、教学过程:1.导入:(1)初步了解学生对乘法和除法的概念及应用情况(2)通过简单的问题,激发学生对乘除法的兴趣2.讲解:(1)介绍乘法的概念及表示方法,讲解口诀“因数相乘,积”的用法(2)介绍除法的概念及表示方法,讲解口诀“被除数除以除数,商”的用法(3)讲解填空格的方法及应用示例3.练习:(1)通过填空格的方式,巩固乘除法的概念及应用(2)以实际问题为背景,出示填空格练习题,并引导学生用乘除法解决问题4.拓展:(1)通过三位数的乘法、除法口算例题,拓展学生的计算技能(2)通过游戏的形式,让学生在愉悦的氛围中巩固乘除法的口诀及运用技能5.归纳:(1)复习乘法、除法及口诀的知识要点(2)回顾填空格练习题及实际问题的解决过程与思路6.作业:(1)完成乘法、除法的口诀默写(2)完成填空格练习题(3)探究乘除法在实际生活中的应用五、教学评价:通过对学生的口算、填空格及解决实际问题的表现,评价学生对乘除法的掌握情况及应用能力。
同时,通过对学生的思维及探究能力的观察,评价学生对数学学习的态度及认知程度。
七、教学方法:本次课程采用多种教学方法,如直观教学法、情境教学法、探究性教学法和游戏教学法等,旨在激发学生的学习兴趣和主动性,提高他们的学习效果。
在教学过程中,教师将重点放在引导学生思考和解决问题上,让学生充分参与,在教师和学生相互配合的情况下,相互促进,共同达成目标。

目录加法与减法 (2)基本应用题 (4)和差倍问题之一 (10)盈亏与比较 (15)数列规律 (20)加减法填空空格 (25)乘除法填空格 (29)几何图形认知 (33)枚举法 (36)智巧趣题 (39)乘法与除法 (43)等差数列 (47)和差倍问题之二 (50)鸡兔同笼 (52)间隔与方阵问题 (54)数字问题 (56)算符、括号与算式 (57)长度与角度 (59)简单抽屉原理 (61)加法与减法各种加法和减法的速算与巧算方法,如凑整,运算顺序的改变,数的组合与分解,利用基准数等。
1、计算:9998+998+99+9+69998+998+99+9+6=(10000-2)+(1000-2)+(100-1)+(10-1)+6=10000+1000+100+10+(6-2-2-1-1)=111102、计算:1966+1976+1986+1996+20061966+1976+1986+1996+2006=(1986-21)+(1986-10)+1986+(1986+10)+(1986+20)=1986×5-(20+10-10-20)=99303、计算:1234+2341+3412+41231234+2341+3412+4123=(1000+200+30+4)+(2000+300+40+1)+(3000+400+10+2)+(4000+100+20+3)=(1000+2000+3000+4000)+(200+300+400+100)+(30+40+10+20)+(4+1+2+3)=10000+1000+100+10=111104、计算:123+234+345-456+567-678+789-890123+234+345-456+567-678+789-890=123+234+345+(567-456)+(789-678)-890=123+234+345+111+111-890=234+(123+567)-890=234+690-890=34+890-890=345、569+384+147-328-167-529569+384+147-328-167-529=(569-529)+147-(147+20)+388-4-328=40-20+56=766、计算:6472-(4476-2480)+5319-(3323-1327)+9354-(7358-5362)+6839-(4843-2847)6472-(4476-2480)+5319-(3323-1327)+9354-(7358-5362)+6839-(4843-2847)=(6480-8)+(5320-1)+(9360-6)+(6840-1)-(4476-2476-4)-(3323-1323-4)-(7358-5358-4)-(4843-2843-4)=(6480+5320)+(9360+6840)-8-1-6-1-2000+4-2000+4-2000+4-2000+4=11800+16200-8000-16+16=28000-8000=200007、计算:93+87+88+79+100+62+75+95+85+69+72+98+89+77+54+75+92+85+83+76+65+60+79+86+100+49+97+97+80+7893+87+88+79+100+62+75+95+85+69+72+98+89+77+54+75+92+85+83+76+65+60+79+86+100+49+97+97+80+78 =90+3+90-3+90-2+80-1+100+60+2+80-5+90+5+80+5+70-1+70+2+100-2+90-11+80-3+50+4+80-5+90+2+80+5+ 80+3+80-4+70-5+60+80-1+90-4+100+50-1+100-3+100-3+80+80-2=90×7+80×11+100×5+60×2+70×3+50×2-(1+1+1+4+1+1+3+3)=630+800+500+120+210+100-15=2440-15=24258、(1)在加法算式中,如果一个加数增加50,另一个加数减少20,计算和的增加或减少量。
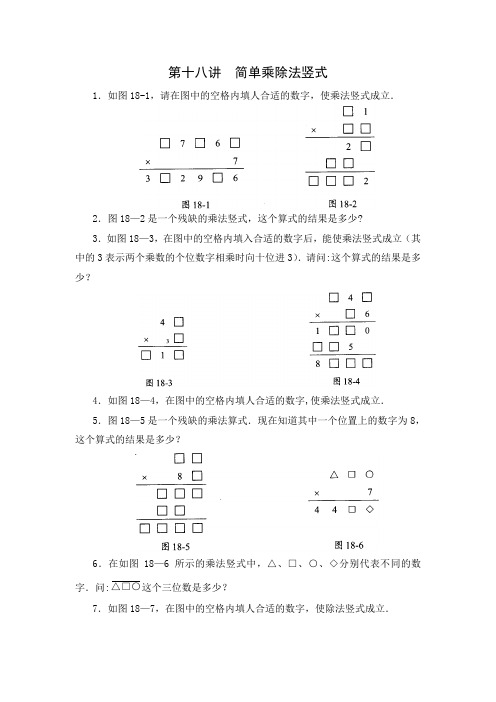
第十八讲简单乘除法竖式1.如图18-1,请在图中的空格内填人合适的数字,使乘法竖式成立.2.图18—2是一个残缺的乘法竖式,这个算式的结果是多少?3.如图18—3,在图中的空格内填入合适的数字后,能使乘法竖式成立(其中的3表示两个乘数的个位数字相乘时向十位进3).请问:这个算式的结果是多少?4.如图18—4,在图中的空格内填人合适的数字,使乘法竖式成立.5.图18—5是一个残缺的乘法算式.现在知道其中一个位置上的数字为8,这个算式的结果是多少?6.在如图18—6所示的乘法竖式中,△、□、○、◇分别代表不同的数字.问:△□○这个三位数是多少?7.如图18—7,在图中的空格内填人合适的数字,使除法竖式成立.8.如图18-8,在图中的空格内填入合适的数字,使除法竖式成立.9.如图18-9,在图中的空格内填人合适的数字,使除法竖式成立.10.如图18-10,在图中的空格内填人合适的数字,使除法竖式成立.1.如图18—11,在图中的空格内填人合适的数字,使乘法竖式成立.2.如图18—12,在图中的空格内填人合适的数字,使乘法竖式成立.3.如图18-13,在图中的空格内填入合适的数字,使乘法竖式成立.4.如图18—14,在图中的空格内填入合适的数字,使乘法竖式成立.5.在图18-15所示的乘法竖式中,有些数字被三角形纸片盖住了.请问:算式的结果是多少?6.图18-16是一个残缺的乘法算式,请补充完整并求出这个算式的结果.7.如图18-17所示的竖式中,不同的汉字代表不同的数字,“车”、“马"、“炮”分别代表什么数字?8.如图18-18,在图中的空格内填人合适的数字,使除法竖式成立.9.如图18-19,在图中的空格内填入合适的数字,使除法竖式成立.10.如图18-20,在图中的空格内填入合适的数字,使除法竖式成立.11。
图18—21是一个残缺的除法竖式,这个算式中的被除数是多少?12。
在如图18—22所示的竖式中,不同的汉字代表不同的数字.请找出每一个汉字对应的数字,并把这个竖式写出来.1.如图18—23,在图中的空格内填入1、2、3、4、5、6、8这几个数字(其中2已经填好),每个数字使用一次,使竖式成立.2.如图18-24,在图中的空格内填人合适的数字,使乘法竖式成立.3.如图18—25,在图中的空格内填入合适的数字,使乘法竖式成立.4.如图18—26,在图中的空格内填入合适的数字,使乘法竖式成立.5.在如图18-27所示的竖式中,不同的符号代表不同的数字,请找出每一个符号对应的数字,并把这个竖式写出来.6.如图18-28,在图中的每个方框内填人一个不是2的数字,可以使其成为正确的算式,求所得的乘积.7.在图18-29的除法竖式中,除了给出的数字4外,空格内的数字都不是4,求算式的被除数.8.图18—30是一个四位数除以一个一位数的除法竖式,图18-31是这个四位数除以另一个一位数的除法竖式,求这个四位数.。

奥数题及答案:乘除法填空格奥数题及答案:乘除法填空格编者导语:“题海无边,题型有限”。
数学必须要有扎实的基本功,有了扎实的基本功再进行“奥数”的学习就显得水到渠成了。
希望数学网店铺整理的三年级奥数题及参考答案:乘除法填空格2,可以帮助到你们,一分耕耘一分收获,相信大家通过自己的努力,一定能够取得优异的!!难度:一个四位数被一个一位数除得图7-15中的①式,而被另一个一位数除得图7-15中的②式,求这个四位数。
此主题相关图片如下:【答案】由第一个算式可知,被除数千位为1;由于除数不可能是1,至少是2,又由于两个商的'百位不可能都是1,那么,如果第二个算式的除数大于第一个除数,即至少是3,且百位均不为1,有五种可能:3*4=12、3*5=15、3*6=18、4*4=16、5*2=10;如果第二个除数是3,那么第一个除数就只能是2,由第一个算式可知显然不行,因为被除数前两位最小是10,而商最大为4。
所以,两个除数只能是3、4,3、5或4、5;如果是3、4,由第二个除数是4,被除数的前两位可以确定是16,且比较两个算式,由后一个可知后两位也只能是16,但对第一个不符,所以,3、4也不可能;如果是3、5,由第二个除数是5,被除数的前两位可以确定是10,百位只能是3,个位不能满足;剩下4、5时,同样分析可知不符合;再看,如果第二个算式的除数小于第一个除数,且百位均不为1,因为第一个除数最大为4,所以只有4、3,4、2和3、2三种可能;4、3显然不符;同样可以分析4、2也不符;只有是3、2时,分析可得到1014满足要求。
如果有一个商的百位是1,显然只能是第一个算式才可能,那么,被除数前两位只能是10,且除数只能是9;结合第二个算式,第二个除数只能是2或5,如为2,百位只能是1,不符;如为5,当百位是3时,可以同时满足两个算式,这时被除数为1035;所以,这个四位数有可能是1014、1035下载全文。

华数思维训练导引――计算问题(二)乘法与除法1.算式333×625×125×25×5×16×8×4×2的结果中末尾有多少个零?解答:找出算式中含有5的是:625×125×25×5=(5×5×5×5)×(5×5×5)×(5×5)×5,共10个5;找出算式中含有2的是:16×8×4×2=(2×2×2×2)×(2×2×2)×(2×2)×2,共10个2。
每一组5×2=10,产生1个0,所以共有10个0。
答:结果中末尾有10个零。
2.如果n=2×3×5×7×11×13×17×125。
那么n的各位数字的和是多少?解答:2×3×5×7×11×13×17×125=(7×11×13) ×(3×17) ×(2×5×125)=1001×51×1250=1001×(50×1250+1×1250)=1001×(12500÷2+1250)=1001×(62500+1250)=(1000+1)×63750=63750000+63750=638137506+3+8+1+3+7+5+0=33答:n的各位数字的和是33.3.(1)计算:5÷(7÷11)÷(11÷15)÷(15÷21),(2)计算:(11×10×9…×3×2×1)÷(22×24×25×27).解答:(1)5÷(7÷11)÷(11÷15)÷(15÷21)=5×11÷7×15÷11×21÷15=5×11÷11×15÷15×21÷7=5×21÷7=5×3×7÷7=5×3=15(2)(11×10×9…×3×2×1)÷(22×24×25×27)=(11×10×9…×3×2×1)÷22÷24÷25÷27)=(11×2÷22) ×(10×5÷25) ×(9×6 ÷27) ×(8×3÷24) ×7×4=1×2×2×1×7×4=4×28=1124.在算式(□□-7×□)÷16=2的各个方框内填入相同的数字后可使等式成立,求这个数字.解答:□□-7×□=11×□-7×□=□×(11-7)=□×4,因为□×4÷16=2,所以□×4=32,□=8答:□=8.5. 计算:9×17+91÷17-5×17+45÷17.解答:9×17+91÷17-5×17+45÷17=9×17-5×17+91÷17+45÷17=(9-5)×17+(91+45)÷17=4×17+136÷17=68+8=766. 计算:567×142+426×811-8520×50.解答:567×142+426×811-8520×50=567×142+3×142×811-8520×100÷2 .=142×(567+3×811)-852000÷2=142×3000-426000=426000-426000=07. 计算:28×5+2×4×35+21×20+14×40+8×62.解答:28×5+2×4×35+21×20+14×40+8×62=2×2×7×5+2×4×5×7+3×7×4×5+2×7×5×2×4+8×62=2×2×7×5×(1+2+3+4)+496=10×14×10+496=1400+496=18968. 计算:55×66+66×77+77×88+88×99.解答:55×66+66×77+77×88+88×99=(11×5)×(11×6)+(11×6)×(11×7)+(11×7)×(11×8)+(11×8)×(11×9)=11×11×(5×6+6×7+7×8+8×9)=11×(10+1)×(30+42+56+72)=(110+11)×200=121×200=242009. 计算:(123456+234561+345612+456123+561234+612345) ÷7.解答:(123456+234561+345612+456123+561234+612345) ÷7=[(1×100000+2×10000+3×1000+4×100+5×10+6)+(2×100000+3×10000+4×1000+5×100+6×10+1)+(3×100000+4×10000+5×1000+6×100+1×10+2)+(4×100000+5×10000+6×1000+1×100+2×10+3)+(5×100000+6×10000+1×1000+2×100+3×10+4)+(6×100000+1×10000+2×1000+3×100+4×10+5)] ÷7=[1+2+3+4+5+6]×100000+(2+3+4+5+6+1)×10000+(3+4+5+6+1+2)×1000+(4+5+6+1+2+3)×100+(5+6+1+2+3+4)×10+(6+1+2+3+4+5)×1] ÷7=(21×100000+21×10000+21×1000+21×100+21×10+21×1)÷7=21×100000÷7+21×10000÷7+21×1000÷7+21×100÷7+21×10÷7+21×1÷7=300000+30000+3000+300+30+3=33333310. (87+56+73+75+83+63+57+53+67+78+65+77+84+62) ÷14.解答:(87+56+73+75+83+63+57+53+67+78+65+77+84+62) ÷14=[(8+5+7+7+8+6+5+5+6+7+6+7+8+6)×10+(7+6+3+5+3+3+7+3+7+8+5+7+4+2)]÷14=[(14×7-7)×10+(14×7-28)] ÷14=[(13×7)×10+(10×7)]÷14=(130+10)×7÷14=140×7÷14=10×7=7011.在算是12345679×□=888888888,12345679×○=555555555的方框和圆圈内分别填入恰当的数后可使两个等式都成立,求所填的两个数之和.解答:□×9个位是8,○×9个位是5,所以□的个位是2,○的个位是5。
第十八讲简单乘除法竖式1.如图18-1,请在图中的空格内填人合适的数字,使乘法竖式成立.2.图18-2是一个残缺的乘法竖式,这个算式的结果是多少?3.如图18-3,在图中的空格内填入合适的数字后,能使乘法竖式成立(其中的3表示两个乘数的个位数字相乘时向十位进3).请问:这个算式的结果是多少?4.如图18-4,在图中的空格内填人合适的数字,使乘法竖式成立.5.图18-5是一个残缺的乘法算式.现在知道其中一个位置上的数字为8,这个算式的结果是多少?6.在如图18-6所示的乘法竖式中,△、□、○、◇分别代表不同的数字.问:△□○这个三位数是多少?7.如图18-7,在图中的空格内填人合适的数字,使除法竖式成立.8.如图18-8,在图中的空格内填入合适的数字,使除法竖式成立.9.如图18-9,在图中的空格内填人合适的数字,使除法竖式成立.10.如图18-10,在图中的空格内填人合适的数字,使除法竖式成立.1.如图18-11,在图中的空格内填人合适的数字,使乘法竖式成立.2.如图18-12,在图中的空格内填人合适的数字,使乘法竖式成立.3.如图18-13,在图中的空格内填入合适的数字,使乘法竖式成立.4.如图18-14,在图中的空格内填入合适的数字,使乘法竖式成立.5.在图18-15所示的乘法竖式中,有些数字被三角形纸片盖住了.请问:算式的结果是多少?6.图18-16是一个残缺的乘法算式,请补充完整并求出这个算式的结果.7.如图18-17所示的竖式中,不同的汉字代表不同的数字,“车”、“马”、“炮”分别代表什么数字?8.如图18-18,在图中的空格内填人合适的数字,使除法竖式成立.9.如图18-19,在图中的空格内填入合适的数字,使除法竖式成立.10.如图18-20,在图中的空格内填入合适的数字,使除法竖式成立.11.图18-21是一个残缺的除法竖式,这个算式中的被除数是多少?12.在如图18-22所示的竖式中,不同的汉字代表不同的数字.请找出每一个汉字对应的数字,并把这个竖式写出来.1.如图18-23,在图中的空格内填入1、2、3、4、5、6、8这几个数字(其中2已经填好),每个数字使用一次,使竖式成立.2.如图18-24,在图中的空格内填人合适的数字,使乘法竖式成立.3.如图18-25,在图中的空格内填入合适的数字,使乘法竖式成立.4.如图18-26,在图中的空格内填入合适的数字,使乘法竖式成立.5.在如图18-27所示的竖式中,不同的符号代表不同的数字,请找出每一个符号对应的数字,并把这个竖式写出来.6.如图18-28,在图中的每个方框内填人一个不是2的数字,可以使其成为正确的算式,求所得的乘积.7.在图18-29的除法竖式中,除了给出的数字4外,空格内的数字都不是4,求算式的被除数.8.图18-30是一个四位数除以一个一位数的除法竖式,图18-31是这个四位数除以另一个一位数的除法竖式,求这个四位数.。
三年级上学期第八讲,数字谜第02讲乘除法填空格【内容概述】利用竖式运算法则和推理,通过观察、判断、推理、尝试把较简单的乘除法竖式算式中缺少的数填出.【典型问题】【基础题】1.【10801】(导引奇数题,三上第08讲,乘除法填空格,数字谜第02讲★★)把1至9这9个不同的数字分别填在图7—1的各个方格内,可使加法和乘法两个算式都成立.现有3个数字的位置已确定,请你填上其他数字.图7-12.【10802】(导引偶数题,三上第08讲,乘除法填空格,数字谜第02讲★)图7—2是一个乘法算式.当乘积最大时,方框内所填的4个数字之和是多少?3.【10803】(导引奇数题,三上第08讲,乘除法填空格,数字谜第02讲★)请补全图7—3所示的残缺算式,问其中的被乘数是多少?4.【10804】(导引偶数题,三上第08讲,乘除法填空格,数字谜第02讲★★)图7—4是一个残缺的乘法竖式,那么乘积是多少?5.【10805】(导引奇数题,三上第08讲,乘除法填空格,数字谜第02讲★★)图7—5是一个残缺的乘法算式,只知道其中一个位置上数字为8,那么这个算式的乘积是多少?6.【10806】(导引偶数题,三上第08讲,乘除法填空格,数字谜第02讲★★)图7-6是一个残缺的乘法算式,补全后它的乘积是多少?7.【10807】(导引奇数题,三上第08讲,乘除法填空格,数字谜第02讲★★★)在图7—7所示的残缺算式中只知道3个位置上的数字是4,那么补全后它的乘积是多少?8.【10808】(导引偶数题,三上第08讲,乘除法填空格,数字谜第02讲★★)图7—8是一个残缺的乘法算式,补全后这个算式的乘积应是多少?9.【10809】(导引奇数题,三上第08讲,乘除法填空格,数字谜第02讲★★)图7-9是一个残缺的乘法算式,补全后这个算式的乘积应是多少?10. 【10810】(导引偶数题,三上第08讲,乘除法填空格,数字谜第02讲★★)图7—10中的竖式由1,2,3,4,5,6,7,8中的7个数码组成,请将空缺的数码填上,使得竖式成立.11.【10811】(导引奇数题,三上第08讲,乘除法填空格,数字谜第02讲★★)在图7—11所示除法竖式的每个方框中,填入适当的数字,使算式成立.那么算式中的被除数是多少?12. 【10812】(导引偶数题,三上第08讲,乘除法填空格,数字谜第02讲★★)补全图7—12所示的除法算式.图7-117213. 【10813】(导引奇数题,三上第08讲,乘除法填空格,数字谜第02讲★★)补全图7-13所示的残缺除法算式,问其中的被除数应是多少?14. 【10814】(导引偶数题,三上第08讲,乘除法填空格,数字谜第02讲★★)按照图7—14中给出的各数字的奇偶性补全这个除法算式.8 7图7-12图7-13图7-146偶15. 【10815】(导引奇数题,三上第08讲,乘除法填空格,数字谜第02讲★★★★)一个四位数被一个一位数除得图7-15中的①式,而被另一个一位数除得图7-15中的②式,求这个四位数.16. 【10816】(汪岩、三上第08讲,乘除法填空格,数字谜第02讲★★)在下面的乘法竖式中,不同的汉字代表不同的数字,相同的汉字代表相同的数字,请将这个竖式补充完。
《仁华学校数学思维训练导引》解析(三年级)➢仁华思维导引解析1讲:加法与减法
➢仁华思维导引解析2讲:基本应用题
➢仁华思维导引解析3讲:和差倍问题之一
➢仁华思维导引解析4讲:盈亏与比较
➢仁华思维导引解析5讲:数列规律
➢仁华思维导引解析6讲:加减法填空格
➢仁华思维导引解析7讲:乘除法填空格
➢仁华思维导引解析8讲:几何图形认知
➢仁华思维导引解析9讲:枚举法
➢仁华思维导引解析10讲:智巧趣题
➢仁华思维导引解析11讲:乘法与除法
➢仁华思维导引解析12讲:等差数列
➢仁华思维导引解析13讲:和差倍问题之二
➢仁华思维导引解析14讲:鸡兔同笼
➢仁华思维导引解析15讲:间隔与方阵问题
➢仁华思维导引解析16讲:数字问题
➢仁华思维导引解析17讲:算符、括号与算式
➢仁华思维导引解析18讲:数阵图初步
➢仁华思维导引解析19讲:长度与角度
➢仁华思维导引解析20讲:简单抽屉原则
仁华思维导引解析1讲:加法与减法
仁华思维导引解析2讲:基本应用题
仁华思维导引解析3讲:和差倍问题之一
仁华思维导引解析4讲:盈亏与比较
仁华思维导引解析5讲:数列规律
仁华思维导引解析6讲:加减法填空格
仁华思维导引解析7讲:乘除法填空格
仁华思维导引解析8讲:几何图形认知
仁华思维导引解析9讲:枚举法。
第07讲数字谜问题第02讲乘除法填空格例1把1~9这九个不同的数字分别填在图7—1的各个方格内,可使加法和乘法两个算式都成立.现有三个数字的位置已确定,请你填上其他数字.答案17×4=68,68+25=93.分析在解乘法竖式的数字谜问题时,会经常使用枚举法试算.本题中,很重要的一个条件就是九个数字各不相同.知道了这一点,再使用枚举法就好了很多.‘详解因为九个数字各不相同,所以第一个乘数的十位只可能填1,如果填2、4、5都不可能使第一个乘法竖式成立,而17×4=68满足第一个乘法竖式.此时,数字谜变为一个加法竖式.因为和数的个位为3,所以第二个加数的个位为5.在九个数字中,现在只有2和9没有填过,因此可以很容易的知道68+25=93.评注此题关键是第一个乘法竖式,一个两位数乘一个一位数等于六十多,那么枚举的情况就很少了.况且所填的数字中不能有3,即情况就更少了.于是就可以比较容易地得出答案.例2请补全如图7-2所示的残缺算式.问其中的被乘数是多少?答案47568.分析在解乘法竖式数字谜问题时,要特别注意首位和末位,也要注意进位.此时的进位比加法要复杂一些,因此使用枚举法.详解先看末位:一个数字乘以7,个位是6,那么这个数只能是8.7×8=56,向十位进了“5”.而6×7:42。
因此积数的十位等于7,并且向百位进了“4”.9-4=5,因此乘数的百位数字乘以7所得的积的个位数字为5,所以乘数的百位数字只能是5.5×7=35,向干位进“3”.7×7=49,49+3=52,向万位进了“5”.因此乘数的万位数字乘以7所得的积大于25小于35,只有4×7=28满足条件.因此整个算式为:47568 × 7=322976.评注乘法的进位比加法复杂得多.两个数字相乘,可以向高位进位,而且在本题中还需要根据积的个位数字来推断乘数,而个位数字的确定也与进位有关.由此可知进位的重要性.例3 图7—3是一个残缺的乘法算式,只知道其中一个位置上数字为8,那么这个算式的乘积是多少?答案 1068.分析这个问题未知数很多,表面看上去很难,突破口就是“8”这个数字.第一个乘数乘以8是一个两位数,那么这个乘数的范围就很小了,而且这个乘数乘上第二个乘数的个位数字是一个三位数,所以第二个乘数的个位数字一定大于8,只可能是9.详解由分析可知,第二个乘数等于89.而第一个乘数只可能是10、ll或12,否则乘8后所得的积就是一个三位数,而11乘以9等于99,是_个两位数,不满足题中的要求.所以第一个乘数一定是12.12×89=1068评注解题时要善于找到突破口,这要求同学们具有很强的分析和推理能力,并且要对题中所涉及的知识点非常熟悉,运用自如.有些问题已知条件较少,那么这不多的几个条件往往就是突破口,它们包含了很重要的信息,应格外注意.例4在图7—4所示的残缺算式中只知道三个位置上的数字是4,那么补全后它的乘积是多少?答案 3243.分析这里只给出了三个4,第一个乘数首位为4,它乘上第二个乘数的个位数字所得的积为一个首位为4的三位数.这个条件很重要.利用枚举法和反证法推出所有的需要补伞的数字.使得竖式成立.详解第一个乘数最大是49,如果第二个乘数的个位为8,那么49×8=392,小于400.所以第二个乘数的个位数字只可能等于9.进一步可以推出第一个乘数的个位数字一定大于或等于5,否则第一个乘数乘上9以后肯定小于400.于是第一个乘数的个位数字只可能是5、6、7、8、9中的一个.如果第一个乘数的个位是5,那么45×9=405.因此第二个乘数的十位数字乘上45所得的积的个位数字应该等于4(否则两个乘数的积的十位数字就不可能等于4),而45乘任何一个数之后,个位只能等于0或5,不等于4,所以第一个乘数的个位不等于5.同样可以知道第一个乘数的个位也不可能等于6、8和9.而当第一个乘数的个位数字等于7时,47×9=23,并且47×6=282,正好可以满足两个乘数的积的十位等于4.我们还可以知道47乘上6以外的其他任何一个数字,个位都不可能等于2,因此答案是惟一的:47×69=3243.评注这道题对分析能力要求很高,首先要推出第二个乘数的个位为9,然后再推出第一个乘数的个位等于7.在详解中,只用反证法证明了第一个乘数的个位不等于5,大家可以类似地证明它不可能等6、8和9.例5图7-5是一个残缺的乘法算式,补全后这个算式的乘积应是多少?答案1862.分析本题和上一题的解法是类似的,要用到枚举法和反证法.详解因为20×90=1800,所以第二个乘数的十位只能是9,否则最后的结果就小于1800.而18×99<1800,所以第一个乘数只能是19.再根据乘法算式的第3行,容易判断出第二个乘数的个位是8.所以这个算式的乘积应该是19×98=1862.评注这道题使用了枚举法,而且计算量很大,枚举法使用了很多次.这种思路比较简单,计算也不是很复杂,认真地计算,不怕麻烦,多试几次就可以很容易地得出答案.例6在图7-6所示除法竖式的每个方框中填人适当的数字,使算式成立,那么算式中的被除数是多少?答案2919.分析将273分解质因数,得273=13×7×3.再利用题中其他信息推出除数,就可很容易地得出被除数是多少了.详解由273=13×7×3,知除数只可能是39或91.如果除数是39,那么39x 2=78,是一个两位数,不符合要求.所以除数肯定是91,那么商的十位数为3.所以被除数为:91×32+7=2919.评注此题关键是要将273分解质因数.由题中可以看出273等于一个两位数(除数)乘以一个一位数(商的十位数字),所以会很自然地想到将273分解质因数.这样可能的情况就很少了,用枚举法和反证法,稍加分析就很明了了.例7补全如图7-7所示的残缺除法算式.问其中的被除数应是多少?答案 11087.分析首先应该看到在除法竖式中,余数是98,而余数肯定是小于除数的,因此除数只可能是99.然后再仔细分析除法竖式的结构,可以很容易地得出答案.详解由以上分析可知除数一定是99.再看除法竖式的特点,发现99乘以商中的每一个数字所得的积都是两位数,因此商中的每一个数字都是1,即商等于111.所以,被除数为:99×111+98=11087.评注此题表面上很复杂,但是根据98可以得到很多信息.另外,大家在解除法竖式数字谜问题时经常会用到下面这个等式:除数×商+余数=被除数.而且有下面这个重要的不等式:除数>余数.例8 一个四位数被一个一位数除得图7-8中的①式,而被另一个一位数除得图7-8中的②式.求这个四位数.答案 1014或1035.分析这是一道很巧的题,条件很少,主要从竖式的结构去挖掘条件,而且要两个竖式联合起来考虑.详解首先被除数的首位一定等于1,百位为0,第一个竖式的除数乘以商的首位等于9.两个数相乘等于9,只有两种情况:3×3=9或者9×1=9.所以第一个竖式的除数等于3或者9.若第一个竖式的除数为3,那么由第二个竖式可知被除数的十位数字只能为1或2.试算一下,综合两个竖式就可知被除数为1014,此时第二个竖式的除数为2.若第一个竖式的除数为9,看第二个竖式,因为被除数的前两位分别1和0,所以第二个竖式的除数只能是2或5.若是2,试算一下,很容易知道不满足题目条件.因此,第二个竖式的除数是5.试算一下就可知被除数是1035.因此答案有两个:1014和1035.评注此题有两个答案,所以在使用枚举法和试探法时,一定要注意完整性,不要找到一个符合条件的就停止了,这样很容易遗漏掉一些情况.在这里,我们将两个竖式综合起来考虑,需要很强的综合分析能力,要求大家掌握从整体进行分析的思想.。