(四)相贯的画法
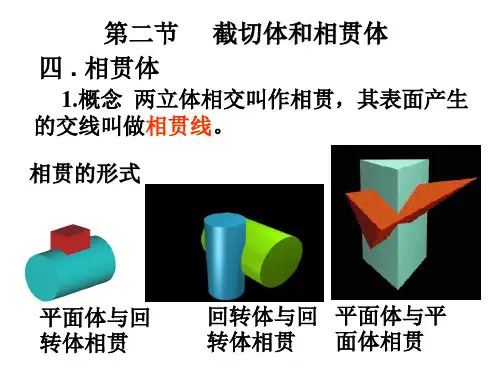
相贯---两立体(回转体)表面相交,其交线称为相贯线。 1、相贯线的性质:
共有性:相贯线是相交两立体表面的共有线,也是 两立体表面的分界线。 封闭性:由于立体均具有一定的范围,所以相贯线 一般由封闭的空间曲线。
相贯线的形状取决于立体的几 何性质、相对大小以及它们的相 对位置。
2、相贯线的作图方法: 辅助平面法———三面共点原理 原则: 要求辅助平面与立体表面交线的投影应为直线或圆.
PH
3、相贯线的简化画法
1´
2´
3’(4’)
1”(2”)
4”
3”
找特殊点; 作垂直平分线,得到圆心和半径。
4、相贯线的特殊情况
1)柱柱等直径相贯
2)有公共内切球--柱锥相贯
5、组合相贯线
例1
例2、两空心圆筒垂直相贯
本次课教学内容小结
教学主要内容: 用辅助平面法求相贯线
求相贯线的思路与方法: 由给定的视图分析相贯立体表面的几何性质、相贯两立 体的相对位置和大小、相贯两立体相对于投影面的位置;
相贯线的作图步骤:
(1)形体面的位置;
b´
(2)求相贯线上的特殊点
(3)求一系列中间点,选 正平面作为辅助面
(4)根据虚实性光滑连线
4’ 1’(2’)
2
3
4
b 1
Pw
3”4”
2”
b”
1”
PH
相贯线的作图步骤:
(1)形体分析
(2)求相贯线上的特殊点 (3)求一系列中间点 (4)根据虚实性光滑连线
分析相贯线可以通过何种辅助平面求出,要求辅助平面与 两立体表面的交线的投影分别是简单易画的图线-直线或 圆;
找出相贯线上的特殊点;