十年真题(2010-2019)高考数学(文)分类汇编专题06 平面向量(新课标Ⅰ卷)(原卷版)

专题01集合历年考题细目表历年高考真题汇编1．【2019年新课标1文科02】已知集合U＝{1，2，3，4，5，6，7}，A＝{2，3，4，5}，B＝{2，3，6，7}，则B∩∁U A＝（）A．{1，6} B．{1，7} C．{6，7} D．{1，6，7}【解答】解：∵U＝{1，2，3，4，5，6，7}，A＝{2，3，4，5}，B＝{2，3，6，7}，∴∁U A＝{1，6，7}，则B∩∁U A＝{6，7}故选：C．2．【2018年新课标1文科01】已知集合A＝{0，2}，B＝{﹣2，﹣1，0，1，2}，则A∩B＝（）A．{0，2} B．{1，2}C．{0} D．{﹣2，﹣1，0，1，2}【解答】解：集合A＝{0，2}，B＝{﹣2，﹣1，0，1，2}，则A∩B＝{0，2}．故选：A．3．【2017年新课标1文科01】已知集合A＝{x|x＜2}，B＝{x|3﹣2x＞0}，则（）A．A∩B＝{x|x} B．A∩B＝∅C．A∪B＝{x|x} D．A∪B＝R【解答】解：∵集合A＝{x|x＜2}，B＝{x|3﹣2x＞0}＝{x|x}，∴A∩B＝{x|x}，故A正确，B错误；A∪B＝{x||x＜2}，故C，D错误；故选：A．4．【2016年新课标1文科01】设集合A＝{1，3，5，7}，B＝{x|2≤x≤5}，则A∩B＝（）A．{1，3} B．{3，5} C．{5，7} D．{1，7}【解答】解：集合A＝{1，3，5，7}，B＝{x|2≤x≤5}，则A∩B＝{3，5}．故选：B．5．【2015年新课标1文科01】已知集合A＝{x|x＝3n+2，n∈N}，B＝{6，8，10，12，14}，则集合A∩B中元素的个数为（）A．5 B．4 C．3 D．2【解答】解：A＝{x|x＝3n+2，n∈N}＝{2，5，8，11，14，17，…}，则A∩B＝{8，14}，故集合A∩B中元素的个数为2个，故选：D．6．【2014年新课标1文科01】已知集合M＝{x|﹣1＜x＜3}，N＝{x|﹣2＜x＜1}，则M∩N＝（）A．（﹣2，1）B．（﹣1，1）C．（1，3）D．（﹣2，3）【解答】解：M＝{x|﹣1＜x＜3}，N＝{x|﹣2＜x＜1}，则M∩N＝{x|﹣1＜x＜1}，故选：B．7．【2013年新课标1文科01】已知集合A＝{1，2，3，4}，B＝{x|x＝n2，n∈A}，则A∩B＝（）A．{1，4} B．{2，3} C．{9，16} D．{1，2}【解答】解：根据题意得：x＝1，4，9，16，即B＝{1，4，9，16}，∵A＝{1，2，3，4}，∴A∩B＝{1，4}．故选：A．8．【2012年新课标1文科01】已知集合A＝{x|x2﹣x﹣2＜0}，B＝{x|﹣1＜x＜1}，则（）A．A⊊B B．B⊊A C．A＝B D．A∩B＝∅【解答】解：由题意可得，A＝{x|﹣1＜x＜2}，∵B＝{x|﹣1＜x＜1}，在集合B中的元素都属于集合A，但是在集合A中的元素不一定在集合B中，例如x∴B⊊A．故选：B．9．【2011年新课标1文科01】已知集合M＝{0，1，2，3，4}，N＝{1，3，5}，P＝M∩N，则P的子集共有（）A．2个B．4个C．6个D．8个【解答】解：∵M＝{0，1，2，3，4}，N＝{1，3，5}，∴P＝M∩N＝{1，3}∴P的子集共有22＝4故选：B．10．【2010年新课标1文科01】已知集合A＝{x||x|≤2，x∈R}，B＝{x|4，x∈Z}，则A∩B＝（）A．（0，2）B．[0，2] C．{0，2} D．{0，1，2}【解答】解：∵A＝{x||x|≤2}＝{x|﹣2≤x≤2}B＝{x|4，x∈Z}＝{0，1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16}则A∩B＝{0，1，2}故选：D．考题分析与复习建议本专题考查的知识点为：集合关系及其运算，历年考题主要以选择填空题型出现，重点考查的知识点为：交并补运算，预测明年本考点题目会比较稳定，备考方向以知识点交并补运算为重点较佳.最新高考模拟试题 1．若集合，，则AB =（ ）A ．B ．C ．D ．【答案】A 【解析】 解：，则，故选：A ． 2．已知集合，，则AB =（ ）A ．[2,3]B ．(1,5)C ．{}2,3D ．{2,3,4}【答案】C 【解析】，，又，所以，故本题选C.3．已知集合，，则A B =（ ）A ．B ．{}1,0,1,2,3-C ．{}3,2--D ．【答案】B 【解析】因为，∴．4．已知全集U =R ，集合，则()U A B =ð（ ）A ．(1,2)B ．(]1,2 C ．(1,3) D ．(,2]-∞【答案】B 【解析】由24x >可得2x >，可得13x <<，所以集合,(,2]U A =-∞ð，所以()U A B =ð(]1,2，故选B.5．已知集合，集合，则集合A B ⋂的子集个数为（ ） A ．1 B ．2C ．3D ．4【答案】D 【解析】由题意得，直线1y x =+与抛物线2y x =有2个交点，故A B ⋂的子集有4个. 6．已知集合，，则()R M N ⋂ð=（ ）A ．{-1，0，1，2，3}B ．{-1，0，1，2}C ．{-1，0，1}D ．{-1，3}【答案】D 【解析】 由题意，集合，则或3}x ≥又由，所以，故选D.7．已知集合，，则()R A B I ð=( )A ．{}1,0-B ．{}1,0,1-C ．{}1,2,3D ．{}2,3【答案】B 【解析】 因为，所以，又，所以.8．已知R 是实数集，集合，，则()AB =Rð（ ）A ．{}1,0-B ．{}1C ．1,12⎡⎤⎢⎥⎣⎦D ．1,2⎛⎫-∞ ⎪⎝⎭【答案】A 【解析】即故选A 。

2010—2019“十年高考”数学真题分类汇总平面向量专题（附详细答案解析）一、选择题。

1.（2019全国Ⅰ文8）已知非零向量a ，b 满足a =2b ，且（a –b ）⊥b ，则a 与b 的夹角为 A ．π6 B ．π3 C ．2π3 D ．5π6【答案】B ．【解析】因为()-⊥a b b ，所以()22cos ,0-⋅⋅-=⋅<>-=a b b =a b b a b a b b ，所以22cos ,2<>===⋅bba b a bb又因为0,]π[<>∈，a b ，所以π,3<>=a b ．故选B ． 2.（2019全国Ⅱ文3）已知向量a =(2，3)，b =(3，2)，则|a –b |= AB ．2C ．D ．50 【答案】A ．【解析】因为(2,3)=a ，(3,2)=b ，所以-(1,1)=-a b ，所以-==a b A.3.（2018全国卷Ⅰ）在∆ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB = A ．3144AB AC - B ．1344AB AC - C ．3144AB AC + D ．1344AB AC + 【答案】A.【解析】法一、通解 如图所示，CB AD DB ED EB 2121+=+= ()()AC AB AC AB -++⨯=212121 3144=-AB AC ．故选A ．CB法二、优解111()222=-=-=-⨯+EB AB AE AB AD AB AB AC 3144=-AB AC ．故选A ． 4.（2018全国卷Ⅱ）已知向量a ，b 满足||1=a ，1⋅=-a b ，则(2)⋅-=a a b A ．4B ．3C ．2D ．0【答案】B.【解析】2(2)22(1)3⋅-=-⋅=--=a a b a a b ，故选B ．5.（2018天津）在如图的平面图形中，已知1OM =，2ON =，120MON ∠=，2BM MA =， 2CN NA =，则·BC OM 的值为 A ．15- B ．9- C ．6- D ．0【答案】C.【解析】由2BM MA =，可知||2||BM MA =，∴||3||BA MA =． 由2CN NA =，可知||2||CN NA =，∴||3||CA NA =，故||||3||||BA CA MA NA ==，连接MN ，则BC MN ∥，且||3||BA MN =， ∴33()BC MN ON OM ==-，∴23()3()BC OM ON OM OM ON OM OM ⋅=-⋅=⋅-23(||||cos120||)6ON OM OM =-=-．故选C ．6.（2018浙江）已知a ，b ，e 是平面向量，e 是单位向量．若非零向量a 与e 的夹角为3π，向量b 满足2430-⋅+=b e b ，则||-a b 的最小值是A 1B 1C ．2D ．2 【答案】A.【解析】解法一 设O 为坐标原点，OA =a ，(,)OB x y ==b ，=(1,0)e ，由2430-⋅+=b e b 得22430x y x +-+=，即22(2)1x y -+=，所以点B 的轨迹是以(2,0)C 为圆心，l 为半径的圆．NMOCBA因为a 与e 的夹角为3π，所以不妨令点A在射线y =(0x >)上，如图，数形结合可知min ||||||31CA CB -=-=-a b ．故选A ．解法二 由2430-⋅+=b e b 得2243()(3)0-⋅+=-⋅-=b e b e b e b e ．设OB =b ，OE =e ，3OF =e ，所以EB -=b e ，3FB -b e =，所以0EB FB ⋅=，取EF 的中点为C ．则B 在以C 为圆心，EF 为直径的圆上，如图．设OA =a ，作射线OA ，使得3AOE π∠=，所以|||(2)(2)|-=-+-≥a b a e e b|(2)||(2)|||||31CA BC ---=-≥a e e b ．故选A ．7.（2017北京）设m , n 为非零向量，则“存在负数λ，使得λ=m n ”是“0⋅<m n ”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】A.【解析】因为,m n 为非零向量，所以||||cos ,0⋅=<><m n m n m n 的充要条件是cos ,0<><m n ．因为0λ<，则由λ=m n 可知,m n 的方向相反，,180<>=m n ，所以cos ,0<><m n ，所以“存在负数λ，使得λ=m n ”可推出“0⋅<m n ”；而0⋅<m n 可推出cos ,0<><m n ，但不一定推出,m n 的方向相反，从而不一定推得“存在负数λ，使得λ=m n ”，所以“存在负数λ，使得λ=m n ”是“0⋅<m n ”的充分而不必要条件．8.（2017浙江）如图，已知平面四边形ABCD ，AB BC ⊥,2AB BC AD ===,3CD =， AC 与BD 交于点O ，记1I OA OB =⋅，2·I OB OC ＝，3·I OC OD ＝，则 OABCDA ．1I <2I <3IB ．1I <3I <2IC ．3I < 1I <2ID ．2I <1I <3I【答案】C 。

2010年高考数学试题分类汇编——向量（2010江苏卷）15、（本小题满分14分）在平面直角坐标系xOy 中，点A(－1,－2)、B(2,3)、C(－2,－1)。

(1)求以线段AB 、AC 为邻边的平行四边形两条对角线的长； (2)设实数t 满足(OC t AB -)·OC =0，求t 的值。

[解析]本小题考查平面向量的几何意义、线性运算、数量积，考查运算求解能力。

满分14分。

（1）（方法一）由题设知(3,5),(1,1)AB AC ==-u u u r u u u r ，则所以|||AB AC AB AC +=-=u u u r u u u r u u u r u u u r故所求的两条对角线的长分别为、（方法二）设该平行四边形的第四个顶点为D ，两条对角线的交点为E ，则:E 为B 、C 的中点，E （0，1）又E （0，1）为A 、D 的中点，所以D （1，4）故所求的两条对角线的长分别为BC=、AD=（2）由题设知：OC u u u r =(－2,－1)，(32,5)AB tOC t t -=++u u u r u u u r 。

由(OC t AB -)·OC =0，得：(32,5)(2,1)0t t ++⋅--=，从而511,t =-所以115t =-。

或者：2· AB OC tOC =u u u r u u u r u u u r ，(3,5),AB =u u u r 2115||AB OC t OC ⋅==-u u u r u u u r u u u r （2010江苏卷）15、（本小题满分14分）在平面直角坐标系xOy 中，点A(－1,－2)、B(2,3)、C(－2,－1)。

(3)求以线段AB 、AC 为邻边的平行四边形两条对角线的长； (4)设实数t 满足(OC t AB -)·OC =0，求t 的值。

[解析]本小题考查平面向量的几何意义、线性运算、数量积，考查运算求解能力。

2010年高考数学试卷分类汇编——向量（2010湖南文数）6.若非零向量a ，b 满足||||,(2)0a b a b b =+⋅=，则a 与b 的夹角为 A. 300 B.600 C. 1200 D. 1500（2010全国卷2理数）（8）ABC V 中，点D 在AB 上，CD 平方ACB ∠．若C B a =u r ，CA b =uu r ，1a =，2b =，则CD =uu u r（A ）1233a b +（B ）2133a b + （C ）3455a b + （D ）4355a b + 【答案】B【命题意图】本试卷主要考查向量的基本运算，考查角平分线定理. 【解读】因为CD 平分ACB ∠，由角平分线定理得AD CA 2=DB CB 1=，所以D 为AB 的三等分点，且22AD AB (CB CA)33==-，所以2121CD CA+AD CB CA a b 3333==+=+，故选B.（2010辽宁文数）（8）平面上,,O A B 三点不共线，设,OA a OB b ==,则OAB ∆的面积等于（A 222()a b a b -⋅ （B 222()a b a b +⋅（C 222()a b a b -⋅ （D 222()a b a b +⋅解读：选C.222111(||||sin ,||||1cos ,||||1222||||OABa S ab a b a b a b a b a b ∆⋅=<>=-<>=-222()a b a b =-⋅（2010辽宁理数）(8)平面上O,A,B 三点不共线，设,OA=a OB b =，则△OAB 的面积等于【答案】C【命题立意】本题考查了三角形面积的向量表示，考查了向量的内积以及同角三角函数的基本关系。

【解读】三角形的面积S=12|a||b|sin<a,b>，而=11|||||||sin ,22a b a b a b =<>（2010全国卷2文数）（10）△ABC 中，点D 在边AB 上，CD 平分∠ACB ，若CB = a , CA = b ,a = 1 ，b = 2, 则CD =（A ）13a +23b （B ）23a +13b （C ）35a +45b （D ）45a +35b 【解读】B ：本题考查了平面向量的基础知识∵ CD 为角平分线，∴12BD BC AD AC ==，∵AB CB CA a b =-=-，∴222333AD AB a b==-，∴22213333CD CA AD b a b a b=+=+-=+（2010安徽文数）(3)设向量(1,0)a =,11(,)22b =,则下列结论中正确的是(A)a b = (B)22a b =(C)//a b (D)a b -与b 垂直 3.D【解读】11(,)22--a b =，()0a b b -=，所以-a b 与b 垂直. 【规律总结】根据向量是坐标运算，直接代入求解，判断即可得出结论.（2010重庆文数）（3）若向量(3,)a m =，(2,1)b =-，0a b =，则实数m 的值为 （A ）32-（B ）32（C ）2 （D ）6解读：60a b m =-=，所以m =6（2010重庆理数）(2) 已知向量a ，b 满足0,1,2,a b a b ∙===，则2a b -=A. 0B.C. 4D. 8 解读：2a b -=22844)2(222==+⋅-=-b b a a b a（2010山东文数）（12）定义平面向量之间的一种运算“”如下：对任意的(,)a m n =，(,)b p q =，令a b mq np =-，下面说法错误的是(A)若a 与b 共线，则0a b =(B)a b b a =(C)对任意的R λ∈，有()()a b ab λλ=(D)2222()()||||ab a b a b +∙=答案：B（2010四川理数）（5）设点M 是线段BC 的中点，点A 在直线BC 外，216,B C A B A C A B A C =∣+∣=∣-∣,则AM ∣∣=（A ）8 （B ）4 （C ） 2 （D ）1解读：由2BC ＝16，得|BC |＝4AB AC AB AC BC ∣+∣=∣-∣=||＝4而AB ACAM ∣+∣=2∣∣ 故AM ∣∣=2 答案：C（2010天津文数）（9）如图，在ΔABC 中，AD AB ⊥，3BC =BD ，1AD =，则AC AD ⋅=（A ）（B ）2 （C ）3（D【答案】D【解读】本题主要考查平面向量的基本运算与解三角形的基础知识，属于难题。

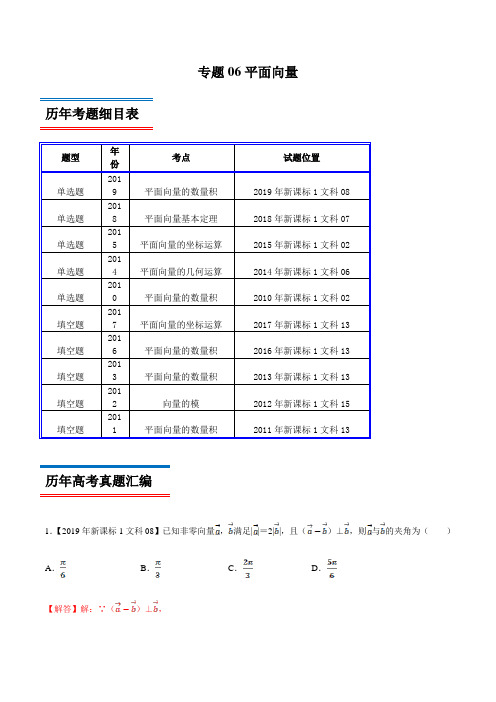
专题06平面向量历年考题细目表题型年份考点试题位置单选题2019 平面向量的数量积2019年新课标1文科08单选题2018 平面向量基本定理2018年新课标1文科07单选题2015 平面向量的坐标运算2015年新课标1文科02单选题2014 平面向量的几何运算2014年新课标1文科06单选题2010 平面向量的数量积2010年新课标1文科02填空题2017 平面向量的坐标运算2017年新课标1文科13填空题2016 平面向量的数量积2016年新课标1文科13填空题2013 平面向量的数量积2013年新课标1文科13填空题2012 向量的模2012年新课标1文科15填空题2011 平面向量的数量积2011年新课标1文科13历年高考真题汇编1．【2019年新课标1文科08】已知非零向量，满足||＝2||，且（）⊥，则与的夹角为（）A．B．C．D．【解答】解：∵（）⊥，∴，∴，∵，∴．故选：B．2．【2018年新课标1文科07】在△ABC中，AD为BC边上的中线，E为AD的中点，则（）A．B．C．D．【解答】解：在△ABC中，AD为BC边上的中线，E为AD的中点，（），故选：A．3．【2015年新课标1文科02】已知点A（0，1），B（3，2），向量（﹣4，﹣3），则向量（）A．（﹣7，﹣4）B．（7，4）C．（﹣1，4）D．（1，4）【解答】解：由已知点A（0，1），B（3，2），得到（3，1），向量（﹣4，﹣3），则向量（﹣7，﹣4）；故选：A．4．【2014年新课标1文科06】设D，E，F分别为△ABC的三边BC，CA，AB的中点，则（）A．B．C．D．【解答】解：∵D，E，F分别为△ABC的三边BC，CA，AB的中点，∴（）+（）（），故选：A．5．【2010年新课标1文科02】平面向量，已知（4，3），（3，18），则夹角的余弦值等于（）A．B．C．D．【解答】解：设（，y），∵a＝（4，3），2a+b＝（3，18），∴∴cosθ，故选：C．6．【2017年新课标1文科13】已知向量（﹣1，2），（m，1），若向量与垂直，则m＝．【解答】解：∵向量（﹣1，2），（m，1），∴（﹣1+m，3），∵向量与垂直，∴（）•（﹣1+m）×（﹣1）+3×2＝0，解得m＝7．故答案为：7．7．【2016年新课标1文科13】设向量（，+1），（1，2），且⊥，则＝．【解答】解：∵；∴；即+2（+1）＝0；∴．故答案为：．8．【2013年新课标1文科13】已知两个单位向量，的夹角为60°，t（1﹣t）．若•0，则t ＝．【解答】解：∵，，∴0，∴t cos60°+1﹣t＝0，∴10，解得t＝2．故答案为2．9．【2012年新课标1文科15】已知向量夹角为45°，且，则．【解答】解：∵， 1∴∴|2|解得故答案为：310．【2011年新课标1文科13】已知a与b为两个垂直的单位向量，为实数，若向量与向量垂直，则＝．【解答】解：∵∴∵垂直∴即∴＝1 故答案为：1 考题分析与复习建议本专题考查的知识点为：平面向量的线性运算，平面向量基本定理及坐标表示，平面向量的数量积，平面向量的综合应用等.历年考题主要以选择填空题型出现，重点考查的知识点为：平面向量的线性运算，平面向量基本定理及坐标表示，平面向量的数量积等，预测明年本考点题目会比较稳定，备考方向以知识点平面向量的线性运算，平面向量的数量积，平面向量的综合应用等为重点较佳.最新高考模拟试题1．在ABC ∆中，2AB AC AD +=u u u r u u u r u u u r ，0AE DE +=u u u r u u u r r，若EB xAB y AC =+u u u r u u u r u u u r ，则（ ）A ．3y x =B ．3x y =C ．3y x =-D ．3x y =-【答案】D 【解析】因为2AB AC AD +=u u u v u u u v u u u v ，所以点D 是BC 的中点，又因为0AE DE +=u u u v u u u v v，所以点E 是AD 的中点，所以有：11131()22244BE BA AE AB AD AB AB AC AB AC =+=-+=-+⨯+=-+u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u uv u u u v ，因此31,344x y x y =-=⇒=-，故本题选D.2．已知非零向量a r ,b r 的夹角为60o,且满足22a b -=r r ,则a b ⋅r r 的最大值为( )A ．12B ．1C ．2D ．3【答案】B 【解析】因为非零向量a r ,b r 的夹角为60o,且满足22a b -=r r ,所以2222444a b a b a b -=+-⋅=r r rr r r ，即2244cos 604a b a b +-=or r r r ，即22424a b a b +-=r r r r ，又因为2244a b a b +≥r rr r ，当且仅当2a b =r r 时，取等号；所以222424a b a b a b ≤+-=r r rr r r ，即2a b ≤r r ；因此，1cos 6012a b a b a b ⋅==≤or r r r r r .即a b ⋅r r 的最大值为1.故选B3．设a r ，b r 均为单位向量，则“a r 与b r夹角为2π3”是“||a b +=r r ( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件【答案】D 【解析】因为a r ，b r均为单位向量， 若a r 与b r夹角为2π3，则||1a b +=r r ；因此，由“a r 与b r 夹角为2π3”不能推出“||a b +=r r ”；若||a b +=r r ，则||a b +===r r解得1cos ,2a b =v v ，即a r 与b r 夹角为π3，所以，由“||a b +=r r ”不能推出“a r 与b r 夹角为2π3”因此，“a r 与b r 夹角为2π3”是“||a b +=r r ”的既不充分也不必要条件.故选D4．在矩形ABCD 中，4AB =uu u r ,2AD =u u u r ．若点M ，N 分别是CD ，BC 的中点，则AM MN ⋅=u u u u r u u u u r（ ）A ．4B ．3C ．2D ．1【答案】C【解析】由题意作出图形，如图所示：由图及题意，可得：12AM AD DM AD AB =+=+u u u u r u u u r u u u u r u u u r u u u r ，1122MN CN CM CB CD =-=-u u u u r u u u r u u u u r u u u r u u u r 11112222BC DC AD AB =-+=-+u u u r u u u r u u ur u u u r .∴111222AM MN AD AB AD AB ⎛⎫⎛⎫⋅=+⋅-+ ⎪ ⎪⎝⎭⎝⎭u u u u r u u u u r u u u r u u u r u u u r u u u r 221111||||41622424AD AB =-⋅+⋅=-⋅+⋅=u u u r u u u r .故选：C ．5．已知P 为等边三角形ABC 所在平面内的一个动点，满足()BP BC R λλ=∈u u u r u u u r，若2AB =u u u r ，则()AP AB AC u u u v u u u v u u u v⋅+=（ ）A ．23B ．3C ．6D ．与λ有关的数值【答案】C 【解析】如图：以BC 中点为坐标原点O ，以BC 方向为x 轴正方向，OA 方向为y 轴正方向，建立平面直角坐标系，因为2AB =u u u r ，则3AO =u u u r因为P 为等边三角形ABC 所在平面内的一个动点，满足()BP BC R λλ=∈u u u r u u u r，所以点P 在直线BC ，所以AP uu u r 在AO u u ur 方向上的投影为AO u u u v ，因此2()226AP AB AC AO AP AO ⋅+=⋅==u u u r u u u r u u u r u u u r u u u r u u u r .故选C6．已知向量(2,1),(,1)a b m ==-r r ，且()a a b ⊥-rr r ，则m 的值为（ ）A ．1B ．3C ．1或3D ．4【答案】B 【解析】因为(2,1),(,1)a b m ==-r r ，所以(2,2)a b m -=-rr ，因为()a a b ⊥-rr r ，则()2(2)20a a b m ⋅-=-+=r r r ，解得3m =所以答案选B.7．已知向量a r 、b r 为单位向量，且a b +r r 在a r 31+，则向量a r 与b r 的夹角为（ ）A ．6π B ．4π C ．3π D ．2π 【答案】A 【解析】设向量a r 与b r的夹角为θ， 因为向量a r 、b r为单位向量，且a b +r r 在a r 31，则有3()||12a b a a ⎛⎫+⋅=+ ⎪ ⎪⎝⎭r r r r ，变形可得：3112a b +⋅=+rr ，即3 cos c2 1o1sa bθθ⋅=⨯⨯==rr，又由0θπ≤≤，则6πθ=，故选A．8．在矩形ABCD中，3,4,AB AD AC==与BD相交于点O，过点A作AE BD⊥，垂足为E，则AE EC⋅=u u u v u u u v（）A．725B．14425C．125D．1225【答案】B【解析】如图：由3AB=，4=AD得：9165BD=+=，125AB ADAEBD⋅==又()AE EC AE EO OC AE EO AE OC AE EO AE AO⋅=⋅+=⋅+⋅=⋅+⋅u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u rAE BD⊥Q0AE EO∴⋅=u u u r u u u r又2144cos25AEAE AO AE AO EAO AE AO AEAO⋅=∠=⋅==u u u ru u u r u u u r u u u r u u u r u u u r u u u r u u u ru u u r14425AE EC∴⋅=u u u r u u u r本题正确选项：B9．已知直线y=+m和圆2+y2=1交于A、B两点，O为坐标原点，若3AO AB2⋅=u u u r u u u r，则实数m=（）A．1±B．3C．22±D．12±【答案】C【解析】联立221y x mx y =+⎧⎨+=⎩ ，得22+2m+m 2-1=0， ∵直线y=+m 和圆2+y 2=1交于A 、B 两点，O 为坐标原点， ∴△=4m 2+8m 2-8=12m 2-8＞0，解得m或m ＜，设A （1，y 1），B （2，y 2），则1+2=-m ，21212m x x -= ， y 1y 2=（1+m ）（2+m ）=12+m （1+2）+m 2，AO u u u r=（-1，-y 1），AB u u u v=（2-1，y 2-y 1），∵21123,2AO AB AO AB x x x ⋅=∴⋅=-u u u r u u u r u u u r u u u r +y 12-y 1y 2=1221122m m ----+m 2-m 2=2-m 2=32， 解得m=2±． 故选：C ．10．已知菱形ABCD 的边长为2，120BAD ∠=︒，点E ，F 分别在边BC ，DC 上，3BC BE =，DC DF λ=，若1AE AF ⋅=u u u r u u u r，则λ的值为（ ）A ．3B ．2C ．23D ．52【答案】B 【解析】 由题意可得：()()AE AF AB BE AD DF ⋅=+⋅+u u u r u u u r u u u r u u u r u u u r u u u r113AB BC BC AB λ⎛⎫⎛⎫+⋅+ ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r u u u r 22111133AB BC AB BC λλ⎛⎫=+++⋅ ⎪⎝⎭u u u r u u u r u u ur u u u r ，且：224,22cos1202AB BC AB BC ==⋅=⨯⨯=-o u u u r u u u r u u u r u u u r，故()44112133λλ⎛⎫+++⨯-= ⎪⎝⎭，解得：2λ=. 故选：B .11．已知正ABC ∆的边长为4，点D 为边BC 的中点，点E 满足AE ED u u u r u u u r =，那么EB EC ⋅u u u r u u u r的值为（ ） A ．83- B ．1-C ．1D ．3【答案】B 【解析】由已知可得：7， 又23tan BED 3BD ED ∠===所以221tan 1cos 1tan 7BED BEC BED -∠∠==-+∠ 所以1||cos 7717EB EC EBEC BEC ⎛⎫⋅=∠=-=- ⎪⎝⎭u u u r u u u r u u u r u u u r ‖ 故选：B ．12．在ABC ∆中，3AC =，向量AB u u u v 在AC u u u v上的投影的数量为2,3ABC S ∆-=，则BC =( ) A ．5 B ．7C 29D ．42【答案】C 【解析】∵向量AB u u u v 在AC u u u v上的投影的数量为2-，∴||cos 2AB A =-u u u r．①∵3ABC S ∆=，∴13||||sin ||sin 322AB AC A AB A ==u u u r u u u r u u ur ， ∴||sin 2AB A =u u u r．②由①②得tan 1A =-，∵A为ABC∆的内角，∴34Aπ=，∴2||3sin4 ABπ== u u u r在ABC∆中，由余弦定理得2222232cos323(2942BC AB AC AB ACπ=+-⋅⋅⋅=+-⨯⨯-=，∴BC=故选C．13．在△ABC中，,2,BD DC AP PD BP AB ACu u u r u u u r u u u r u u u r u u u r u u u r u u u rλμ===+，则λμ+=（）A．1-3B．13C．1-2D．12【答案】A【解析】因为,2,BD DC AP PD==u u u r u u u r u u u r u u u r所以P为ABC∆的重心，所以11311,22222AD AB AC AP AB AC=+∴=+u u u r u u u r u u u r u u u r u u u r u u u r,所以1133AP AB AC=+u u u r u u u r u u u r,所以23BP AP AB AB AC=-=-+u u u r u u u r u u u r u u u r u u u r因为BP AB ACλμ=+u u u r u u u r u u u r，所以211=,,333λμλμ-=∴+=-故选：A14．在ABC∆中，543AB BC BC CA CA AB→→→→→→==g g g，则sin:sin:sinA B C=（）A．9:7:8BC．6:8:7D【答案】B【解析】设•••543AB BC BC CA CA AB t ===u u u r u u u r u u u r u u u r u u u r u u u r ，所以5,4,3AB BC t BC CA t CA AB t ⋅=⋅=⋅=u u u r u u u r u u u r u u u r u u u r u u u r，所以cos 5,cos 4,cos 3ac B t ab C t bc A t -=-=-=，所以22222222210,8,6c a b t b a c t c b a t +-=-+-=-+-=-， 得9,7,8a t b t c t =-=-=- 所以sin :sin :sin ::A B C a b c ==9:7:8故选：B15．在平行四边形ABCD 中，113,2,,,32AB AD AP AB AQ AD ====u u u r u u u r u u u r u u u v 若12,CP CQ ⋅=u u u v u u u v则ADC ∠=( )A ．56πB ．34π C ．23π D ．2π 【答案】C 【解析】如图所示,平行四边形ABCD 中, 3,2AB AD ==,11,32AP AB AQ AD ==u u u r u u u r u u u r u u u r ，23CP CB BP AD AB ∴=+=--u u u r u u u r u u u r u u u r u u u r ，12CQ CD DQ AB AD =+=--u u u r u u u r u u u r u u u r u u u r ,因为12CP CQ ⋅=u u u r u u u r,所以2132CP CQ AD AB AB AD ⎛⎫⎛⎫⋅=--⋅-- ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r u u u r u u u r u u u r22214323AB AD AB AD =++⋅u u ur u u u r u u u r u u u r222143232cos 12323BAD =⨯+⨯+⨯⨯⨯∠=, 1cos 2BAD ∠=，,3BAD π∴∠= 所以233ADC πππ∠=-=，故选C.16．已知△ABC 中，22BC BA BC =⋅=-u u u r u u u r u u u r ，．点P 为BC 边上的动点，则()PC PA PB PC ⋅++u u u r u u u r u u u r u u u r的最小值为（ ） A ．2 B ．34-C ．2-D ．2512-【答案】D 【解析】以BC 的中点为坐标原点，建立如图的直角坐标系，可得()()1010B C -，，，，设()()0P a A x y ，，，， 由2BA BC ⋅=-u u u r u u u r，可得()()120222x y x +⋅=+=-，，，即20x y =-≠，， 则()()()101100PC PA PB PC a x a a a y ⋅++=-⋅---+-++u u u r u u u r u u u r u u u r，， ()()()()21312332a x a a a a a =--=---=--21253612a ⎛⎫=-- ⎪⎝⎭，当16a =时，()PC PA PB PC ⋅++u u u r u u u r u u u r u u u r 的最小值为2512-．故选：D ．17．如图Rt ABC ∆中，2ABC π∠=，2AC AB =，BAC ∠平分线交△ABC 的外接圆于点D ，设AB a =u u u r r ，AC b =u u u r r ，则向量AD =u u u r（ ）A ．a b +r rB ．12a b +r rC ．12a b +r rD ．23a b +r r【答案】C 【解析】解：设圆的半径为，在Rt ABC ∆中，2ABC π∠=，2AC AB =， 所以3BAC π∠=，6ACB π∠=，BAC ∠平分线交ABC ∆的外接圆于点D ，所以6ACB BAD CAD π∠=∠=∠=，则根据圆的性质BD CD AB ==，又因为在Rt ABC ∆中，12AB AC r OD ===， 所以四边形ABDO 为菱形，所以12AD AB AO a b =+=+u u u r u u u r u u u r r r．故选：C ．18．在ABC ∆中，90A ∠=︒，1AB =，2AC =，设点D 、E 满足AD AB λ=u u u r u u u r ，(1)AE λ=-u u ur ()AC R λ∈u u u r，若5BE CD ⋅=u u u r u u u r，则λ=（ ） A ．13- B ．2 C ．95D ．3【答案】D 【解析】因为90A ∠=︒，则•0AB AC =u u u r u u u r，所以()()BE CD AE AB AD AC •=-•-u u u r u u u r u u u r u u u r u u u r u u u r22[(1)]()(1)4(1)34AC AB AB AC AC AB λλλλλλλ=--•-=---=---=-u u u u r u u u r u u u r u u u r u u u r u u u r .由已知，345λ-=，则3λ=. 选D .19．已知点C 为扇形AOB 的弧AB 上任意一点，且120AOB ∠=︒，若(,)OC OA OB R λμλμ=+∈u u u r u u u r u u u r，则λμ+的取值范围为（ ）A ．[2,2]-B ．C ．D ．[1,2]【答案】D 【解析】解：设半径为1，由已知可设OB 为轴的正半轴，O 为坐标原点，建立直角坐标系，其中A （12-，B （1，0），C （cos θ，sin θ）（其中∠BOC ＝θ203πθ⎛⎫≤≤⎪⎝⎭有OC OA OB λμ=+u u u r u u u r u u u r（λ，μ∈R ）即：（cos θ，sin θ）＝λ（12-，2）+μ（1，0）；整理得：12-λ+μ＝cos θλ＝sin θ，解得：λ=，μ＝cos θ，则λ+μ=+cos θ=sin θ+cos θ＝2sin （θ6π+），其中203πθ⎛⎫≤≤ ⎪⎝⎭；易知λ+μ=+cos θ=θ+cos θ＝2sin （θ6π+），由图像易得其值域为[1，2] 故选：D ．20．在同一平面内，已知A 为动点，B ，C 为定点，且∠BAC=3π，2ACB π∠≠，BC=1，P 为BC 中点．过点P 作PQ⊥BC 交AC 所在直线于Q ，则AQ uuu r 在BC uuu r方向上投影的最大值是（ ）A ．13B ．12C D ．23【答案】C 【解析】建立如图所示的平面直角坐标系，则B （-12，0），C （12，0），P （0，0）， 由BAC 3π∠=可知，ABC 三点在一个定圆上，且弦BC 所对的圆周角为3π，所以圆心角为23π.圆心在BC 的中垂线即y 轴上，且圆心到直线BC 的距离为132tan 3BCπ=3(0,6，半径为22133()()263+=. 所以点A 的轨迹方程为：22313x y ⎛+= ⎝⎭，则213x ≤ ，则303x -≤< ， 由AQ uuu r 在BC u u u r 方向上投影的几何意义可得：AQ uuu r 在BC u u u r方向上投影为|DP|=||， 则AQ uuu r 在BC u u u r 3故选：C ．21．已知圆22450x y x ++-=的弦AB 的中点为(1,1)-，直线AB 交x 轴于点P ，则PA PB ⋅u u u r u u u r的值为______． 【答案】5- 【解析】设(1,1)M -，圆心(2,0)C -，∵10112MC k -==-+，根据圆的性质可知，1AB k =-，∴AB 所在直线方程为1(1)y x -=-+，即22gRr，联立方程224500x y x x y ⎧++-=⎨+=⎩可得，22450x x +-=，设11(,)A x y ，22(,)B x y ，则1252x x +=-， 令0y =可得(0,0)P ，12121225PA PB x x y y x x ⋅=+==-u u u r u u u r，故答案为：-5．22．已知向量(2,1),(,1)a b λ=-=r r ，若||||a b a b +=-r rr r ，则λ=______．【答案】12【解析】解：()()2,1,,1a b λ=-=r Q r()()2,0,2,2a b a b λλ∴+=+-=--r rr r ；a b a b +=-r r r r Q ；2λ∴+=()()22224λλ∴+=-+；解得12λ=． 故答案为：12． 23．向量()1,2a v=-，()1,0b =-r ，若()()a b a b λ-⊥+r r r r ，则λ=_________.【答案】13【解析】向量()1,2a =-v，()1,0b =-r ，所以()()()2,2,1,2a b a b λλλ-=-+=--r r r r，又因为()()a b a b λ-⊥+r r r r，所以()()0a b a b λ-⋅+=r r r r，即()()21220λλ--⨯-=，解得13λ=，故答案为13. 24．设向量12,e e r r的模分别为1,2，它们的夹角为3π，则向量21e e -r r 与2e r 的夹角为_____．【答案】6π 【解析】()221221242cos33e e e e e e π-⋅=-⋅=-=r r r r r r又21e e -===r r()212212212cos ,2e e e e e e e e e -⋅∴<->===-⋅r r r r r rr r r 向量21e e -rr与r2e 的夹角为：6π 本题正确结果：6π25．已知平面向量a r ，m v ，n v ，满足4a =r ，221010m a m n a n ⎧-⋅+=⎨-⋅+=⎩v v v v v v ，则当m n -=u r r _____，则m v 与n v的夹角最大． 【解析】设a r ，m v ，n v的起点均为O ，以O 为原点建立平面坐标系，不妨设(4,0)a =r ，(,)m x y v=，则222m x y =+u r ，4a m x ⋅=r u r ，由210m a m -⋅+=u r r u r可得22410x y x +-+=，即22(2)3x y -+=，∴m v 的终点M 在以(2,0)为圆心，以3为半径的圆上， 同理n v 的终点N 在以(2,0)为圆心，以3为半径的圆上．显然当OM ，ON 为圆的两条切线时，MON ∠最大，即m v ，n v 的夹角最大．设圆心为A ，则3AM =，∴221OM OA AM =-=，3sin 2MOA ∠=，∴60MOA ∠=︒， 设MN 与x 轴交于点B ，由对称性可知MN x ⊥轴，且2MN MB =，∴322sin 2132MN MB OM MOA ==⋅∠=⨯⨯=. 故答案为：3．26．如图，已知P 是半径为2，圆心角为3π的一段圆弧AB 上一点，2A B B C =u u u v u u u v ，则PC PA ⋅u u u r u u u r 的最小值为_______．【答案】5﹣13【解析】设圆心为O,AB 中点为D,由题得22sin 2,36AB AC π=⋅⋅=∴=.取AC 中点M ，由题得2PA PC PM PC PA AC⎧+=⎨-=⎩u u u v u u u v u u u u v u u uv u u u v u u u v , 两方程平方相减得2221944PC PA PM AC PM ⋅=-=-u u u r u u u r u u u u r u u u r u u u u r ， 要使PC PA ⋅u u u r u u u r 取最小值，就是PM 最小，当圆弧AB 的圆心与点P 、M 共线时，PM 最小.此时DM=221113,()322DM ∴=+=, 所以PM 有最小值为2﹣13， 代入求得PC PA ⋅u u u r u u u r 的最小值为5﹣213．故答案为：5﹣21327．如图，在边长为2的正三角形ABC 中，D 、E 分别为边BC 、CA 上的动点，且满足CE mBD =（m 为定常数，且(0,1]m ∈），若AD DE ⋅u u u r u u u r 的最大值为34-，则m =________.【答案】12【解析】 以BC 中点为坐标原点O ，OC 方向为x 轴正方向，OA 方向为y 轴正方向，建立如图所示平面直角坐标系， 因为正三角形ABC 边长为2，所以(1,0)B -，(1,0)C ，3)A ，则(2,0)BC =u u u r ，(3)CA =-u u u r ，因为D 为边BC 上的动点，所以设BD tBC =u u u r u u u r，其中01t ≤≤， 则(2,0)BD t =u u u r ，所以(21,0)D t -；又CE mBD tmBC ==，所以(3)CE tmCA tm tm ==-u u u r u u u r ，因此(13)E tm tm -，所以(21,3)AD t =-u u u r ，(223)DE tm t tm =--u u u r ，故2(21)(22)32(2)2(3)2AD DE t tm t tm m t m t ⋅=----=-++--u u u r u u u r2223332(2)22(2)222424m m m m t t m t m m m ⎡⎤---⎛⎫⎛⎫⎛⎫=-+--=-+---⎢⎥ ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦223101(2)2424m m m m t m m --+⎛⎫=-+-+ ⎪++⎝⎭， 因为(0,1]m ∈，所以31513,2422434m m m -⎡⎫=-+∈⎪⎢++⎣⎭，又01t ≤≤， 所以当且仅当324m t m -=+时，AD DE ⋅u u u r u u u r 取得最大值， 即21013244m m m -+=-+，整理得221780m m -+=，解得12m =或8m =（舍） 故答案为1228．在ABC ∆中，已知AB 边上的中线1CM =，且1tan A ，1tan C ，1tan B 成等差数列，则AB 的长为________.23【解析】 因为1tan A ，1tan C ，1tan B成等差数列， 所以211tan tan tan C A B =+，即2cos cos cos sin()sin sin sin sin sin sin sin sin C A B A B C C A B A B A B +=+==， 所以2sin 2cos sin sin C C A B =，由正弦定理可得2cos 2c C ab=， 又由余弦定理可得222cos 2a b c C ab +-=，所以222222a b c c ab ab+-=，故2222a b c +=，又因为AB 边上的中线1CM =，所以1CM =u u u u v ，因为()12CM CA CB u u u u v u u u v u u u v =+， 所以22222422cos CM CA CB CA CB CA CB CA CB C =++⋅=++u u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ， 即22224232c b a ab c ab =++⋅=，解23c =. 即AB 的长为23. 故答案为23329．如图，在平面四边形ABCD 中，90CBA CAD ∠=∠=︒，30ACD ∠=︒，AB BC =，点E 为线段BC的中点．若AC AD AE λμ=+u u u r u u u r u u u r (,R λμ∈)，则λμ的值为_______．43 【解析】以A 为原点，建立如图所示的平面直角坐标系，不妨设AB ＝BC ＝2，则有A （0,0），B （2,0），C （2,2），E （2,1），AC ＝2AD ＝2×tan30°＝263，过D 作DF⊥轴于F ，∠DAF＝180°－90°－45°＝45°， DF ＝263sin45°＝6223323⨯=，所以D （233-，33）， AC u u u r ＝（2,2），AD u u u r ＝（233-，33），AE u u u r ＝（2,1），因为AC AD AE λμ=+u u u r u u u r u u u r ， 所以，（2,2）＝λ（233-23+μ（2,1），所以，2322 232λμλμ⎧-+=⎪⎪⎨⎪+=⎪，解得：343λμ⎧=⎪⎪⎨⎪=⎪⎩λμ的值为43故答案为：4330．在平面直角坐标系xOy中，已知()11,A x y，()22,B x y为圆221x y+=上两点，且121212x x y y+=-．若C为圆上的任意一点，则CA CBu u u r u u u rg的最大值为______．【答案】32【解析】因为C为圆2+y2＝1上一点，设C（sinθ，cosθ），则()()1122sin,cos,sin,cosCA x y CB x yθθθθ=--=--u u u r u u u r，∵()11,A x y，()22,B x y为圆221x y+=上两点，∴222211221,1x y x y+=+=，又121212x x y y+=-，∴()()2212121212CA CB x x y y x x sin y y cos sin cosθθθθ⋅=+-+-+++u u u r u u u r()()2212121)2x x y yθϕ=++++222211221212122)2x y x y x x y yθϕ=-++++++1sin()2θϕ=-+，其中1212tany yx xϕ+=+，∵sin()θϕ+∈[﹣1，1]，∴当sin()θϕ+＝1时，CA CB ⋅u u u r u u u r 的最大值为32． 故答案为：32．。

专题15 平面向量的概念、线性运算、平面向量基本定理十年大数据*全景展示平面向量的坐标运算及向量共线的充要条件主要考查平面向量的线性运算及向量共线的充要条件平面向量的坐标运算及向量共线的充要条件考点47平面向量的概念与线性运算1．（2014新课标I ，文6）设F E D ,,分别为ABC ∆的三边AB CA BC ,,的中点，则=+FC EBA. BC B ． 12AD C ． AD D ． 12BC 【答案】C【解析】=+FC EB 11()()22CB AB BC AC +++=1()2AB AC +=AD ，故选C ． 2．（2014福建）在下列向量组中，可以把向量()3,2=a 表示出来的是A ．12(0,0),(1,2)==e eB ．12(1,2),(5,2)=-=-e eC ．12(3,5),(6,10)==e eD ．12(2,3),(2,3)=-=-e e【答案】B【解析】对于A ，C ，D ，都有1e ∥2e ，所以只有B 成立．考点48平面向量基本定理及其应用1．（2020江苏13）在ABC ∆中，4AB =，3AC =，90BAC ∠=︒，D 在边BC 上，延长AD 到P ，使得9AP =，若3()2PA mPB m PC =+-（m 为常数），则CD 的长度是 ．【答案】185【解析】由向量系数33()22m m +-=为常数，结合等和线性质可知321PAPD =，故263PD PA ==，3AD PA PD AC =-==，故C CDA ∠=∠，故2CAD C π∠=-． 在ABC ∆中，3cos 5AC C BC ==；在ADC ∆中，由正弦定理得sin sin CD ADCAD C=∠， 即sin(2)sin 23182cos 23sin sin 55C C CD AD AD C AD C C π-=⋅=⋅=⋅=⨯⨯=．2．（2018•新课标Ⅰ，理6文7）在ABC ∆中，AD 为BC 边上的中线，E 为AD 的中点，则(EB = ) A ．3144AB AC - B ．1344AB AC - C ．3144AB AC + D ．1344AB AC + 【答案】A【解析】在ABC ∆中，AD 为BC 边上的中线，E 为AD 的中点，∴12EB AB AE AB AD =-=- 11()22AB AB AC =-⨯+3144AB AC =-，故选A ．3．（2015新课标Ⅰ，理7）设D 为?ABC 所在平面内一点3BC CD =，则（ ） （A ）1433AD AB AC =-+ (B)1433AD AB AC =- （C ）4133AD AB AC =+ (D)4133AD AB AC =- 【答案】A【解析】由题知11()33AD AC CD AC BC AC AC AB =+=+=+-==1433AB AC -+，故选A ． 4．（2013广东）设a 是已知的平面向量且0≠a ，关于向量a 的分解，有如下四个命题：①给定向量b ，总存在向量c ，使=+a b c ；②给定向量b 和c ，总存在实数和，使λμ=+a b c ；③给定单位向量b 和正数，总存在单位向量c 和实数，使λμ=+a b c ； ④给定正数和，总存在单位向量b 和单位向量c ，使λμ=+a b c ； 上述命题中的向量b ，c 和a 在同一平面内且两两不共线，则真命题的个数是 A ．1 B ．2 C ．3 D ．4【答案】B【解析】利用向量加法的三角形法则，易的①是对的；利用平面向量的基本定理，易的②是对的；以的终点作长度为的圆，这个圆必须和向量有交点，这个不一定能满足，③是错的；利用向量加法的三角形法则，结合三角形两边的和大于第三边，即必须，所以④是假命题．综上，本题选B ．5．（2017江苏）如图，在同一个平面内，向量OA ，OB ，OC 的模分别为1，1，2，OA 与OC 的夹角为α，且tan 7α=，OB 与OC 的夹角为45．若OC =m OA +n OB （m ，n ∈R ），则m n += ．λμμλλμa μλb =+λμλμ+≥b c a【答案】3【解析】由可得72sin 10α=，，由OC =m OA +n OB 得22OC OA mOA nOB OA OC OB mOB OA nOB⎧⋅=+⋅⎪⎨⎪⋅=⋅+⎩，即2cos cos(45)2cos 45cos(45)m n m n ααα⎧=++⎪⎨=++⎪⎩，两式相加得，2(cos cos 45)()(1cos(45))m n αα+=+++，所以22222cos 2cos 4510231cos(45)227221102102m n αα⨯+⨯++===+++⨯-⨯，所以． 6．（2013北京）向量a ，b ，c 在正方形网格中的位置如图所示，若λμ=+c a b (λ，μ∈R )，则= ．【答案】4【解析】 如图建立坐标系，则()1,1a =-，()6,2b =，()1,3c =-．由c a b λμ=+，可得12,2λμ=-=-，∴4λμ=7．(2015北京)在ABC △中，点M ，N 满足2AM MC =，BN NC =，若MN x AB y AC =+，则x =tan 7α=2cos 10α=3m n +=λμ；y = ．【答案】12 16【解析】由1111()3232MN MC CN AC CB AC AB AC =+=+=+-1126AB AC =- =x AB y AC +．所以12x，16y ． 考点49平面向量的坐标运算及平面向量共线的充要条件1．（2019•新课标Ⅱ，文3）已知向量(2,3)a =，(3,2)b =，则||(a b -= ) AB ．2C ．D ．50【答案】A【解析】(2,3)a =，(3,2)b =，∴(2a b -=，3)(3-，2)(1=-，1)，2||(1)a b ∴-=-故选A ． 2．（2013辽宁）已知点(1,3)A ，(4,1)B -，则与向量AB 同方向的单位向量为A ．B ．C ．D ． 【答案】A【解析】，所以，这样同方向的单位向量是． 3．（2011广东）已知向量a =（1，2），b =（1，0），c =（3，4）．若λ为实数， ()λ+∥a b c ，则λ=A ．14B ．12C ．1D ．2【答案】B【解析】(1,2)λλ+=+a b ，由()λ+a b ∥c ，得64(1)0λ-+=，解得λ=124．（2018•新课标Ⅲ，理13）已知向量(1,2)a =，(2,2)b =-，(1,)c λ=．若//(2)c a b +，则λ= ． 【答案】12【解析】向量(1,2)a =，(2,2)b =-，∴2(4,2)a b +=，(1,)c λ=，//(2)c a b +，∴142λ=，解得12λ=．5．(2016新课标，文13) 已知向量a =(m ，4)，b =(3，−2)，且a ∥b ，则m =___________．【答案】6-3455⎛⎫ ⎪⎝⎭，-4355⎛⎫ ⎪⎝⎭，-3455⎛⎫- ⎪⎝⎭，4355⎛⎫- ⎪⎝⎭，(3,4)AB =-||5AB =134(,)555AB =-【解析】因为a ∥b ，所以2430m --⨯=，解得6m =-．6．（2015•新课标Ⅱ，理13）设向量a ，b 不平行，向量a b λ+与2a b +平行，则实数λ= ． 【答案】12【解析】向量a ，b 不平行，向量a b λ+与2a b +平行，(2)2a b t a b ta tb λ∴+=+=+， ∴12t tλ=⎧⎨=⎩，解得实数12λ=．7．(2015江苏)已知向量(2,1)=a ，(1,2)=-b ，若(9,8)m n +=-a b （,m n ∈R ），则m n - 的值为___． 【答案】－3【解析】由题意得：29,282,5, 3.m n m n m n m n +=-=-⇒==-=-8．(2014北京)已知向量a 、b 满足1=a ，(2,1)=b ，且0λ+=a b (R λ∈)，则λ=__．【解析】∵||1=a ，∴可令(cos ,sin )θθ=a ，∵0λ+=a b ，∴cos 20sin 10λθλθ+=⎧⎨+=⎩，即2cos 1sin θλθλ⎧=-⎪⎪⎨⎪=-⎪⎩，解得25λ=得||λ=9．（2014陕西）设20πθ<<，向量()sin 2cos θθ=，a ，()cos 1θ，b ，若∥a b ，则=θtan _______．【答案】12【解析】∵∥a b ，∴2sin 2cosθθ=，∴22sin cos cos θθθ=，∵(0,)2πθ∈，∴1tan 2θ=．。

2019年高考数学试题分项版——平面向量（解析版）一、选择题1．(2019·全国Ⅰ文，8)已知非零向量a ，b 满足|a |＝2|b |，且(a －b )⊥b ，则a 与b 的夹角为( )A.B.C.D.答案 B解析 设a 与b 的夹角为α，∵(a －b )⊥b ，∴(a －b )·b ＝0，∴a ·b ＝b 2，∴|a |·|b |cos α＝|b |2，又|a |＝2|b |，∴cos α＝，∵α∈[0，π]，∴α＝，故选B.2．(2019·全国Ⅱ文，3)已知向量a ＝(2,3)，b ＝(3,2)，则|a －b |等于( ) A. B ．2 C ．5 D ．50 答案 A解析 ∵a －b ＝(2,3)－(3,2)＝(－1,1)， ∴|a －b |＝ ＝ . 即2x ＋y －2π＋1＝0.3．(2019·全国Ⅰ理，7)已知非零向量a ，b 满足|a |＝2|b |，且(a －b )⊥b ，则a 与b 的夹角为( )A.B.C.D.答案 B解析 设a 与b 的夹角为α，∵(a －b )⊥b ，∴(a －b )·b ＝0，∴a ·b ＝b 2，∴|a |·|b |cos α＝|b |2，又|a |＝2|b |，∴cos α＝，∵α∈[0，π]，∴α＝，故选B.4．(2019·全国Ⅱ理，3)已知 ＝(2,3)， ＝(3，t )，| |＝1，则 · 等于( ) A ．－3 B ．－2 C ．2 D ．3 答案 C解析 因为＝ － ＝(1，t －3)，所以| |＝ ＝1，解得t ＝3，所以 ＝(1,0)，所以 · ＝2×1＋3×0＝2，故选C.5．(2019·北京理，7)设点A ，B ，C 不共线，则“AB 与AC 的夹角为锐角”是“||||AB AC BC +>”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【思路分析】“AB 与AC 的夹角为锐角” ⇒ “||||AB AC BC +>”，“ ||||AB AC BC +>” ⇒ “AB 与AC 的夹角为锐角”，由此能求出结果． 【解析】：点A ，B ，C 不共线，“AB 与AC 的夹角为锐角” ⇒ “||||AB AC BC +>”， “||||AB AC BC +>” ⇒ “AB 与AC 的夹角为锐角”，∴设点A ，B ，C 不共线，则“AB 与AC 的夹角为锐角”是“||||AB AC BC +>”的充分必要条件． 故选：C ．【归纳与总结】本题考查充分条件、必要条件、充要条件的判断，考查向量等基础知识，考查推理能力与计算能力，属于基础题． 二、填空题1．(2019·全国Ⅲ文，13)已知向量a ＝(2,2)，b ＝(－8,6)，则cos 〈a ，b 〉＝________. 答案 －解析 ∵a ＝(2,2)，b ＝(－8,6)， ∴a ·b ＝2×(－8)＋2×6＝－4，|a |＝ ＝2 ，|b |＝ ＝10. ∴cos 〈a ，b 〉＝＝＝－. 2．(2019·北京文，9)已知向量a ＝(－4,3)，b ＝(6，m )，且a ⊥b ，则m ＝________. 答案 8解析 ∵a ⊥b ，∴a ·b ＝0. 又∵a ＝(－4,3)，b ＝(6，m )， ∴－4×6＋3m ＝0，解得m ＝8.3．(2019·浙江，17)已知正方形ABCD 的边长为1.当每个λi (i ＝1,2,3,4,5,6)取遍±1时，|λ1 ＋λ2 ＋λ3 ＋λ4 ＋λ5 ＋λ6 |的最小值是________，最大值是________． 答案 0 2解析 以A 为坐标原点，AB 所在直线为x 轴，AD 所在直线为y 轴建立平面直角坐标系，如图，则A (0,0)，B (1,0)，C (1,1)，D (0,1)，所以λ1 ＋λ2 ＋λ3 ＋λ4 ＋λ5 ＋λ6 ＝(λ1－λ3＋λ5－λ6，λ2－λ4＋λ5＋λ6)，所以当 时，可取λ1＝λ3＝1，λ5＝λ6＝1，λ2＝－1，λ4＝1，此时|λ1 ＋λ2 ＋λ3 ＋λ4 ＋λ5 ＋λ6 |取得最小值0；取λ1＝1，λ3＝－1，λ5＝λ6＝1，λ2＝1，λ4＝－1，则|λ1 ＋λ2 ＋λ3 ＋λ4 ＋λ5 ＋λ6|取得最大值＝2.4.(2019·江苏，12)如图，在△ABC中，D是BC的中点，E在边AB上，BE＝2EA，AD与CE交于点O.若·＝6·，则的值是_________．答案解析方法一以点D为坐标原点，BC所在的直线为x轴，BC的垂直平分线为y轴建立平面直角坐标系(图略)，不妨设B(－a,0)，C(a,0)，A(b，c)，a>0，c>0，由BE＝2EA得E，则直线OA：y＝x，直线CE：(b－2a)y＝c(x－a)，联立可得O，则·＝(－a－b，－c)·(a－b，－c)＝b2＋c2－a2，·＝·＝，由·＝6·得b2＋c2－a2＝2(b2＋c2－2ab)，化简得4ab＝b2＋c2＋a2，则＝＝＝.方法二由A，O，D三点共线，可设＝λ，则＝(＋)，由E，O，C三点共线可设＝μ，则－＝μ(－)，则＝(1－μ)＋μ＝(1－μ)＋μ，由平面向量基本定理可得解得μ＝，λ＝，则＝(＋)，＝－＝－，则6·＝6×(＋)·＝＝·，化简得32＝2，则＝.5．(2019·全国Ⅲ理，13)已知a，b为单位向量，且a·b＝0，若c＝2a－b，则cos〈a，c〉＝________.答案解析设a＝(1,0)，b＝(0,1)，则c＝(2，－)，所以cos〈a，c〉＝＝. 6．(2019·天津理，14)在四边形ABCD中，AD∥BC，AB＝2，AD＝5，∠A＝30°，点E 在线段CB的延长线上，且AE＝BE，则·＝________.答案－1解析方法一在等腰△ABE中，易得∠BAE＝∠ABE＝30°，故BE＝2，则·＝(－)·(＋)＝·＋·－2－·＝5×2×cos 30°＋5×2×cos 180°－12－2×2×cos 150°＝15－10－12＋6＝－1.方法二在△ABD中，由余弦定理可得BD＝＝，所以cos∠ABD＝＝－，则sin ∠ABD＝.设与的夹角为θ，则cos θ＝cos(180°－∠ABD＋30°)＝－cos(∠ABD－30°)＝－cos∠ABD·cos 30°－sin∠ABD·sin 30°＝－，在△ABE中，易得AE＝BE＝2，故·＝×2×＝－1.。

专题03 平面向量平面向量小题：10年10考，每年1题，向量题考得比较基础，突出向量的几何运算或代数运算，不侧重于与其它知识交汇，难度不大．这样有利于考查向量的基本运算，符合考试说明．【答案】B2．（2018年）在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB =u u u r（ ）【答案】A【答案】7【解析】∵向量a r ＝（﹣1，2），b r ＝（m ，1），∴a b +r r ＝（﹣1+m ，3），∵向量ab +r r 与a r 垂直，∴()a b a+⋅r r r ＝（﹣1+m）×（﹣1）+3×2＝0，解得m ＝7．5．（2015年）已知点A （0，1），B （3，2），向量C A uuu r ＝（﹣4，﹣3），则向量C B uuu r＝（ ）A ．（﹣7，﹣4）B ．（7，4）C ．（﹣1，4）D ．（1，4）【答案】A【解析】∵点A （0，1），B （3，2），∴AB u u u r＝（3，1），∵C A uuu r ＝（﹣4，﹣3），∴C B uuu r ＝C A -AB u u u r u u u r ＝（﹣7，﹣4），故选A ．6．（2014年）设D ，E ，F 分别为△ABC 的三边BC ，CA ，AB 的中点，则EB u u u r +FC u u u r ＝（ ）A ．D A u u u rB ．1D 2A u u urC ．C B uuu rD ．1C 2B u u ur【答案】A【解析】∵D ，E ，F 分别为△ABC 的三边BC ，CA ，AB 的中点，∴EB u u u r +FC u u u r ＝（F E u u r +F B u u u r ）+（F E u u r +C E u u ur ）＝F B u u u r +C E u u u r ＝()1C 2AB +A u u u r u u u r ＝D A u u u r，故选A ．7．（2013年）已知两个单位向量a r ，b r 的夹角为60°，c r ＝t a r+（1﹣t ）b r ．若b c ⋅r r ＝0，则t ＝ ．【答案】2【解析】∵c r ＝t a r+（1﹣t ）b r，b c ⋅r r ＝0，∴()210b c ta b t b ⋅=⋅+-=r rr r r ，∴t cos60°+1﹣t ＝0，∴1102t -=，解得：t ＝2．8．（2012年）已知向量a r ，b r夹角为45°，且1a =r ，210a b -=r r ，则b r ＝ ．【答案】32【解析】∵45θ=o，1a =r，∴2cos 2a b a b b θ⋅==r r r r r ，∴2a b -r r ＝()22a b-r r ＝2244a a b b-⋅+r r r r ＝2422b b -+r r ＝10，解得：32b =r ．9．（2011年）已知a r 与b r 为两个垂直的单位向量，k 为实数，若向量a r +b r 与向量k a r ﹣b r垂直，则k ＝ ．【答案】1【解析】∵a b ⊥r r ，∴0a b ⋅=r r ，∵a r +b r 与k a r﹣b r 垂直，∴()()0a b ka b +⋅-=r r r r ，即220ka ka b a b b +⋅-⋅-=r r r r r r ，∴k ＝1．10．（2010年）平面向量a r ，b r ，已知a r ＝（4，3），2a b +r r ＝（3，18），则a r ，b r夹角的余弦值等于（ ）【答案】C故选C ．。

第五章 平面向量一 平面向量的概念及基本运算【考点阐述】向量．向量的加法与减法．实数与向量的积．平面向量的坐标表示． 【考试要求】（1）理解向量的概念，掌握向量的几何表示，了解共线向量的概念． （2）掌握向量的加法和减法．（3）掌握实数与向量的积，理解两个向量共线的充要条件．（4）了解平面向量的基本定理.理解平面向量的坐标的概念，掌握平面向量的坐标运算．【2010年湖北卷理5文8】．已知△ABC 和点M 满足++=0．若存在实数m 使得+=m 成立，则m =BA ．2B ．3C ．4D ．5【解析】由MA +MB +MC =0知，点M 为△ABC 的重心，设点D 为底边BC 的中点，则AM =31AD =32·21（AB +AC ）=31（AB +AC ），所以有AB +AC =m AM ，故m =3，选B ．【2010年全国Ⅱ卷理8文10】．△ABC 中，点D 在AB 上，CD 平分∠ACB ．若CB =a ，CA =b ，| a |=1，| b |=1，则CD =B A ．31a +32b B ．32a +31b C ．53a +54b D ．54a +53b 【命题意图】本试题主要考查向量的基本运算，考查角平分线定理.【解析】因为CD 平分∠ACB ，由角平分线定理得CBCADB AD =2，所以D 为AB 的三等分点，且AD =32AB =32（CB ―CA ），所以CD =CA +AD =32CB +31CA =32a +31b ．【2010年陕西卷理11文12】．已知向量a =（2，―1），b =（―1，m ），c =（―1，2），若（a +b ）∥c ，则m = ． 【答案】―1【解析】∵a +b =（1，m ―1），c =（―1，2），∴由（a +b ）∥c得1×2―（―1）×（m ―1）=0，所以m =―1．【2010年高考上海市理科13】．如图所示，直线x =2与双曲线Г：42x ―y 2=1的渐近线交于E 1，E 2两点，记1OE =e 1，2OE =e 2，任取双曲线上的点P ，若=a e 1+b e 2（a ，b ∈R ），则a 、b 满足的一个等式是 ．4ab =1【答案】4ab =1【2010年高考上海卷文科13】．在平面直角坐标系中，双曲线的中心在原点，它的一个焦点坐标为（5，0），e 1=（2，1），e 2=（2，―1）分别是两条渐近线的方向向量。