1 电力拖动系统动力学基础
- 格式:ppt
- 大小:491.00 KB
- 文档页数:12



第一章 电力拖动系统的动力学基础1-1 什么是电力拖动系统?它包括那几部分?都起什么作用?举例说明.答:由原动机带动生产机械运转称为拖动。
用各种电动机作为原动机带动生产机械运动,以完成一定的生产任务的拖动方式,称为电力拖动。
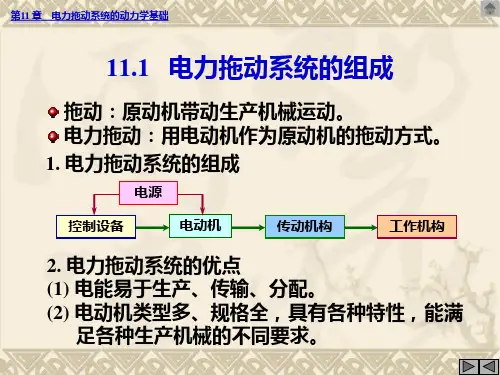
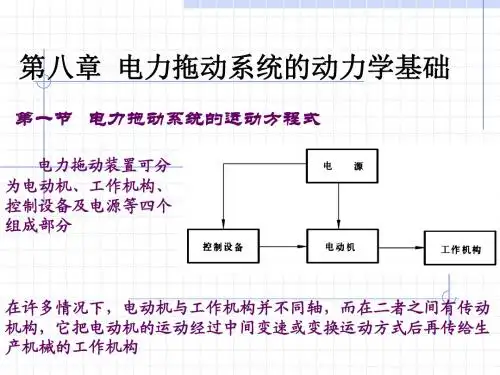
电力拖动系统,一般由电动机、机械传动机构、生产机械的工作机构、控制设备和电源五部分组成。
其中,电动机作为原动机,通过传动机构带动生产机械的工作机构执行某一生产任务;机械传动机构用来传递机械能;控制设备则用来控制电动机的运动;电源的作用是向电动机和其他电气设备供电。
1-2 电力拖动系统运动方式中T ,T n 及n 的正方向是如何规定的?如何表示它的实际方向?答:设转速n 对观察者而言逆时针为正,则转矩T 与n 的正方向相同为正;负载转矩T 与n 的正方向相反为正。
与正方向相同取正,否则取反。
L 1-3 试说明GD 2的概念答:J=gGD 42即工程中常用表示转动惯量的飞轮惯量。
1-4 从运动方程式中如何看出系统是处于加速、减速、稳速或静止等运动状态?答: 当时,L T T >0>dt dn ,系统加速;当L T T <时,0<dt dn ,系统减速。
当 时,L T T =0=dt dn ,转速不变,系统以恒定的转速运行,或者静止不动。
1-5 多轴电力拖动系统为什么要折算为等效单轴系统?答: 多轴电力拖动系统,不同轴上有不同的转动惯量和转速,也有相应的反映电动机拖动的转矩及反映工作机构工作的阻转矩,这种系统比单轴拖动系统复杂,计算较为困难,为了简化计算,一般采用折算的办法,把多轴电力拖动系统折算为等小的单轴系统。
1-6 把多轴电力拖动系统折算为等效单轴系统时负载转矩按什么原则折算?各轴的飞轮力矩按什么原则折算?答:功率相等原则;能量守恒原则.1-7 什么是动态转矩?它与电动机负载转矩有什么区别?答:动态转矩是指转矩是时间的函数. 而负载转矩通常是转速的函数.1-8 负载的机械特性有那几种类性?各有什么特点?答:恒转矩负载特性:与n 无关,总是恒值;恒功率负载特性:与n 成反比例变化;通风机负载特性:与n2成正比例变化。





第一章电力拖动系统的动力学基础本章要求了解有关电力拖动的基本概念;掌握单轴拖动系统的运动方程;重点掌握多轴系统等效为单轴系统后等效的系统负载和系统转动惯量的计算。
本章重点多轴系统向单轴系统的等效折算。
本章简述在电力拖动系统中,为了得到系统中电机和负载的运动和工作情况,需要通过求解动力学方程和利用电机学中的电机方程得到。
然而动力方程只能适用单轴系统,而实际中大多是多轴拖动系统,因此必须将多轴系统通过等效变换为合适的单轴系统来求解。
这就要掌握等效变换的原则和方法。
本章学时2学时第一节单轴电力拖动系统的运动方程式本节学时0.5学时本节重点1、单轴拖动系统运动方程2、转动惯量的单位制转换教学方法结合理论,推导出单轴拖动系统运动的计算公式,掌握其中的单位制变换,以及方程的求解。
教学手段以传统教学手段与电子课件相结合的手段,让学生在有限的时间内掌握更多的相关知识。
教学内容:一、单轴电力拖动系统的运动方程式在图1-1(a)所示电力拖动系统中,作用在该轴上的转矩有电动机的电磁转矩T、电动机的空载转矩T0及生产机械的负载转矩Tm,T+Tm=TL。
TL为电动机的负载转矩,轴的旋转角速度为 。
电动机转子的转动惯量为JR ,生产机械转动部分的转动惯量为Jm。
联轴器的转动惯量比JR 及Jm小很多,可忽略,因此单轴拖动系统对转轴的总转动惯量为J=JR +Jm。
图1-1(b)给出了各物理量的参考正方向。
假定两轴之间为刚性连接,并忽略轴的弹性变形,那么图1-1所示的单轴拖动系统可以看成刚体绕固定轴转动。
根据力学中(a ) 单轴电力拖动系统 (b ) 各量的参考方向图 1-1 单轴电力拖动系统及各量的参考方向刚体转动定律及各量的参考正方向,可写出如下的转动方程式T-T L =Jdt d Ω(1-1) 式中:T —电动机的电磁转矩(N ·m )T L ——电动机的负载转矩(N ·m ),J —电动机轴上的总转动惯量(㎏·㎡), Ω —电动机的角速度(rad/s )式(1-1)称为单轴电力拖动系统的运动方程式,它描述了作用于单轴拖动系统的转矩与速度变化之间的关系,是研究电力拖动系统各种运转状态的基础。
电力拖动系统的动力学基础引言电力拖动系统是一种将电能转化为机械能的系统,广泛应用于各种工业和交通领域。
研究电力拖动系统的动力学基础是理解其工作原理和性能的关键。
本文将介绍电力拖动系统的动力学基础,包括动力学方程、系统稳定性和控制方法等方面的内容。
动力学方程电力拖动系统的动力学方程描述了系统的运动规律。
一般而言,电力拖动系统可以分为两个部分:电动机和负载。
电动机负责产生力和扭矩,将电能转化为机械能;负载则承受电动机输出的力和扭矩。
动力学方程可以用以下方式表示:\\(J\\frac{{d\\omega}}{{dt}} = T_m - T_l - B\\omega\\)其中,\(J\)是系统的转动惯量,\(\omega\)是系统的角速度,\(T_m\)是电动机输出的扭矩,\(T_l\)是负载承受的扭矩,\(B\)是摩擦系数。
动力学方程描述了系统内部各个力和扭矩之间的平衡关系。
当电动机输出的扭矩大于负载承受的扭矩时,系统可以加速。
反之,当负载承受的扭矩大于电动机输出的扭矩时,系统会减速。
系统稳定性电力拖动系统的稳定性是评估系统性能的关键指标之一。
系统稳定性主要取决于电动机的控制方式和系统参数的选取。
闭环控制闭环控制是常用的电力拖动系统控制方式之一。
闭环控制通过不断检测系统的实际输出,与期望输出进行比较,然后调整电动机的输入信号,使得系统能够迅速响应和稳定工作。
闭环控制的动力学方程可以表示为:\\(T_m = K_p(\\omega_r - \\omega) + K_i\\int(\\omega_r - \\omega)dt + K_d\\frac{{d(\\omega_r - \\omega)}}{{dt}}\\)其中,\(T_m\)是电动机输出的扭矩,\(\omega_r\)是期望的角速度,\(\omega\)是实际的角速度,\(K_p\)、\(K_i\)和\(K_d\)是比例、积分和微分增益。
闭环控制能够提高系统的稳定性和响应速度,使得系统能够更好地适应外部负载变化。