第八章 电力拖动系统的动力学基础(Dynamics basis of e-power dragging system)电机拖动系统是用电动机来拖动机械运行的系统。
包括：电动机、传动机构、生产机械、控制设备和电源五个部分。
它们之间的关系如下本章主要介绍电力拖动系统的运动方程、负载转矩特性。
8.1电力拖动系统的运动方程式(kinematics equation)一.运动方程式电力拖动系统运动方程式描述了系统的运动状态，系统的运动状态取决于作用在原动机转轴上的各种转矩。
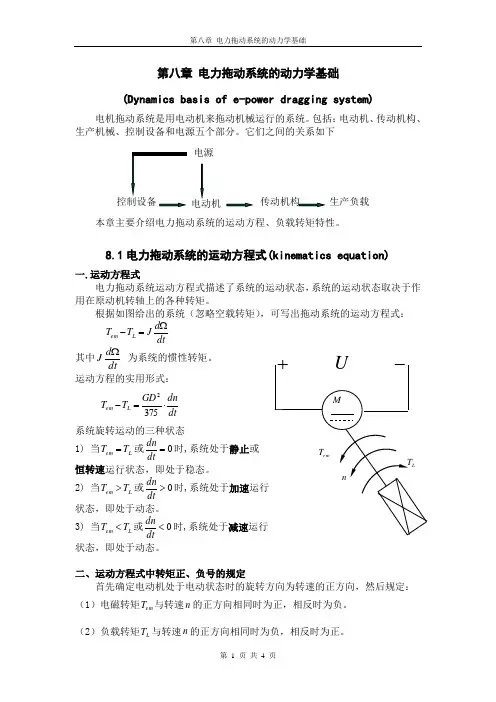
根据如图给出的系统（忽略空载转矩），可写出拖动系统的运动方程式：dtd J T T L em Ω=- 其中dtd J Ω 为系统的惯性转矩。
运动方程的实用形式： dt dn GD T T L em ⋅=-3752 系统旋转运动的三种状态1) 当L em T T =或0=dt dn 时,系统处于静止或 恒转速运行状态，即处于稳态。
2) 当L em T T >或0>dtdn 时,系统处于加速运行状态，即处于动态。
3) 当L em T T <或0<dtdn 时,系统处于减速运行状态，即处于动态。
二、运动方程式中转矩正、负号的规定首先确定电动机处于电动状态时的旋转方向为转速的正方向，然后规定：（1）电磁转矩em T 与转速n 的正方向相同时为正，相反时为负。
（2）负载转矩L T 与转速n 的正方向相同时为负，相反时为正。
传动机构 生产负载控制设备电源（3）惯性转矩dtdn GD ⋅3752的大小和正负号由em T 和L T 的代数和决定。
三、各种形状旋转体转动惯量的计算1.分两种情况1）旋转轴通过该物体重心；2）旋转轴不通过该物体重心；2.几种常见旋转物体转动惯量的计算1）小球； 2）圆环体；3）圆柱体； 4）长方体（过重心）5）长方体（不过重心）； 6）圆锥体；7）圆柱体（圆杆，过重心） 8）圆柱体（圆杆，不过重心）8.2工作机构转矩、力、飞轮力矩和质量的折算(conversion)实际拖动系统为多轴系统，分析较为复杂——简化——引入折算概念——等效为单轴系统。
