下载文档原格式
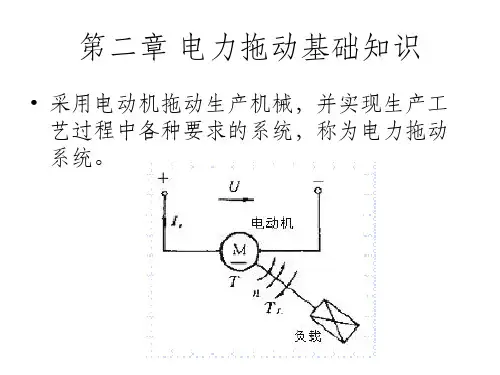
第2章 电力拖动基础的动力学工业生产中最典型的电力拖动系统有电力机车、起重机、龙门刨床等。
由于实际电力拖动系统种类太多，不可能逐一进行研究，所以要找到它们共同的运动规律加以综合分析。
电力拖动系统的运动规律可以用动力学中的运动方程来描述。
为了抓住本质，本章首先分析简单的单轴电力拖动系统动力学行为，然后分析多轴系统的折算问题，典型的负载转矩性质，最后电力拖动系统的平衡稳定运转问题。
2.1单轴电力拖动系统的动力学分析所谓单轴电力拖动系统，就是电动机转子轴直接拖动生产机械运转的系统，如图2.1所示。
图2.1 单轴电力拖动系统示意图单轴电力拖动系统中电磁转矩T 、负载转矩L T 和角速度Ω之间的关系用转动方程式表示为：dt d JT T L Ω=- （2.1）式中，T 为电动机产生的拖动转矩()m N ⋅；L T 为负载转矩()m N ⋅；J 为单轴系统的转动惯量()2m kg ⋅；Ω为单轴系统的角速度()s rad。
工程上，常常不用转动惯量J 而用飞轮惯量或飞轮矩2GD 表示系统的惯性。
系统的速度不用角速度Ω用而转速n 表示。
2GD 与J 之间的关系为gJ GD 42=式中，G 为系统转动部分的重量()N ；D 为系统转动部分的惯性直径()m ；g 为中重力加速度，28.9s mg =。
角速度Ω与转速n 的关系为602nπ=Ω 将上面两式代入运动方程（2.1）式中，化简后得dt dnGD T T L ⋅=-3752 （2.2） 式中，375是一个具有加速度量纲的系数，其单位为1m in -⋅s m ；转矩单位仍为m N ⋅；转速单位仍为min r 。
L T T -称为动态转矩。
当动态转矩为零时，系统处于恒转速运行的稳态；动态转矩大于零时，系统处于加速运动的过渡过程中；动态转矩小于零时，系统处于减速运动的过渡过程中。
运动方程式（2.2）中，由于电动机运行状态的不同和生产机械负载类型的不同，电动机轴上的拖动转矩T 和负载转矩L T 不仅大小不同，方向也是变化的。
