当前位置：文档之家 › 简单辐射传热计算

简单辐射传热计算

  • 格式：ppt
  • 大小：1.24 MB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

No.21 1221 9 辐射传热的计算

No.21 1221 9 辐射传热的计算
有效辐射示意图
8
2、有效辐射J与辐射换热量q之间的关系
从表面1外部来观察，其能量收支差额应等于有效辐射J1与投入辐射G1 之差，即
q J1 G1
E1 (1 )G1 G1 E1 G1
从表面内部观察，该表面与外界的辐射换
热量应为：
q E1 1G1
E q E 1 1 q Eb ( 1)q
已知： tw 15℃ ，
0.9 ，h 20W / m2 K
f w
' ，tw
10 ℃ , 求测温误差？
解: 根据热平衡，对温度计头部，有 A( E E ) h A(t t )
b1 b2
4 4
Eb1w EbA EbE T hA t f t1 bw 1 T 2
17
【例9-4】一直径d=0.75m的圆筒形埋地式加热炉采用电加 热方法加热，如图。在操作过程中需要将炉子顶盖移去一段 时间，设此时筒身温度为500K，筒底为650K。环境温度为 300K，试计算顶盖移去其间单位时间内的热损失。设筒身 及底面均可作为黑体。
20
9-3 多表面系统辐射换热的计算
一、 两表面换热系统的辐射网络
2
1) 2,1 ] X 2,1
根据能量守恒有
1,2 2,1
11
1,2 [ A1 Eb1 (
1
1
1)1,2 ] X1,2 [ A2 Eb 2 (
1
2
1)1,2 ] X 2,1
1, 2
Eb1 Eb 2 1 1 1 1 2 1 A1 A1 X 1, 2 2 A2
（平行平板除外） (4) 若某角系数为0，即空间热阻→∞， 则相应两个表面间可以断开，不连 总热阻个数： ( n＋Cn2 ) 接空间热阻。

传热学-第九章 辐射计算

传热学-第九章 辐射计算

X1, 2
1,2 1,2 A 1,2 B
X1, 2i
i 1
n
A1 Eb1 X 1,2 A1 Eb1 X 1,2 A A1 Eb1 X 1,2 B X 1,2 X 1,2 A X 1,2 B
再来看一下2 对 1 的能量守恒情况: 2 ,1 2 A ,1 2 B ,1
X 1,2 X 2,1
1 A1 1 A2

A1
A2
X d 1, d 2 dA1 X d 2, d 1dA2
A
A1 1
1
cos 1 cos 2 dA1dA2
A2

A1
1 A2
A2

A1
r cos 1 cos 2 dA1dA2
2
(9-4a)
A2
r
2
(9-4b)
的电流、电位差和电阻比拟热辐射中的热流、热势差与热
阻，用电路来比拟辐射热流的传递路径。但需要注意的是， 该方法也离不开角系数的计算，所以，必须满足漫灰面、 物性均匀以及投入辐射均匀的条件。
热势差与热阻
上节公式(9-12)：
J Eb ( 1)q
1

改写为：
Eb J q 1
1, 2 A1 Eb1 X 1, 2 A2 Eb 2 X 2,1 A1 X 1, 2 ( Eb1 Eb 2 ) 的热辐射 到达表面 2的部分 的热辐射 到达表面 1的部分
图9-13 黑体系统的 辐射换热
表面1发出 表面 2发出
例题9-4 一直径d=0.75m的圆筒形埋地式加热炉采用电加热。 在操作过程中需要将炉子顶盖移去一段时间，设此时筒身温 度为 500K ，筒底为 650K 。环境温度为 300K 。试计算顶盖移 去期间单位时间内的热损失。设筒身及底面均可作为黑体。

[工学]传热学-第9章-辐射传热的计算

[工学]传热学-第9章-辐射传热的计算
1. 有效辐射 设有一漫灰表面A，ε=α。 与表面A 有关的能量有： 投入辐射 G 吸收辐射αG 反射辐射ρG
有效辐射法
J
G
G
G
Eb
自身辐射（辐射力）E =εEb 有效辐射 J J E G 或： J Eb (1 )G
合成辐射（净辐射热流）Φ
Φ 1， 2 Eb1
1 1 A1 1
J1
1 A1 X 1, 2
J2
1 2 A2 2
Eb2
9.3.2 多表面封闭系统网络法求解的实施步骤
1. 画出等效的网络图。 三个漫灰表面构成的封闭空腔中的辐射换热
Eb3
1 3 A3 3
1 A1 X 1,3
J3
1 A2 X 2,3
Eb1
1 1 A1 1
(bc ad ) ( ac bd ) 2ab
因此： X 1, 2
9.2 两表面封闭系统的辐射换热
A
2
2 dA
2
9.2.1 黑体表面间的辐射换热
1. 任意位置的两黑体表面。
12 A1 X1, 2 Eb1

2
n1

1
1
r
n2
21 A2 X 2,1Eb 2
dA
1
两黑体表面间的净辐射换热量：

Eb 2 J 2 1 2 A2 2
A2
(c )
A1
A3
换热系统热平衡时：1 2 1,2 将(a),(b),(c)相加，消去J1，J2得：
1, 2 Eb1 Eb 2 1 1 1 1 2 A1 1 A1 X 1, 2 A2 2
或： 1, 2
X 2, 2 1 X 2,1 1

辐射传热的计算

辐射传热的计算
基本定律 ：1. 普朗克定律
2. 斯狄芬-玻耳兹曼定律（维恩位移定律）
3. 兰贝特定律
4.基尔霍夫定律
基本原理： 1.辐射换热的分析与计算（四大部分）
2.遮热板原理的分析与计算

5.67 (1T010
)4

( T2 100
1 1 1
)
4


B(T14
T24 )
1 2
1 2
有板3时，对稳态有： q1,2’=q1,3=q3,2；其中q1,3=B(T14-T34)
图11 遮热板
q3,2=B(T34-T24);而q1,3+q3,2=B(T14-T34)+B(T34-T24)=B(T14-T24)= q1,2
这些都是用减少发射率(吸收比)的方法来削弱换热的例子。
在实际工程应用中，多采用遮热板来减少辐射换热的方法。
所谓遮热板，是指插入两个辐射换热表面之间以削弱辐射 换热的薄板。
如图11所示
假设 1 2 3 只考虑单位面积
无板3时，
q1,2

(Eb1 Eb2 ) 1 1 1
A11 A1 X1,2 A2 2
2. 三灰表面间的辐射换热
应用电学中的基尔霍夫定律， 可列出节点的热流方程：
J1 :
Eb1 J1
1 1

J2
1
J1

J3
1
J1
0
1 A1
A1 X1,2 A1 X1,3
J2 :
Eb2 J 2
12

J1 J2 1

J3 J2 1
0
辐射能的百分数随之而异，从而
影响到换热量。

辐射传热量计算公式

辐射传热量计算公式

辐射传热量计算公式
辐射传热是一种热能的传递方式，其原理是通过热辐射将发热体上的热量传播到其他物体，从而实现热能的传输。

辐射传热量是指辐射传播过程中，一个物体收到另一个物体发出的热辐射能量的总和。

辐射传热量的计算公式是：Q=εσA(T1^4-T2^4)，其中Q是辐射传热量，ε是表面外反射率，σ是每平方米每秒发射的热量，A是物体表面积，T1是物体表面温度，T2是物体周围环境温度。

辐射传热量的计算公式主要是根据辐射传热的物理原理来推导出来的，它可以很好地反映出物体表面温度、外反射率和周围环境温度等多种因素对辐射传热量的影响。

辐射传热的计算公式可以用于室内外热量传输的分析，以及对太阳能热水器、太阳能太阳能热发电系统、热电联产等设备热量分析中，这些设备都是利用辐射传热来实现热能传输的，所以辐射传热量的计算公式在这些设备的设计和分析中有着重要的作用。

辐射传热量的计算公式是根据辐射传热的物理原理推导出来的，它可以反映出多种因素对辐射传热量的影响，它在室内外热量传输的分析，以及对太阳能热水器、太阳能太阳能热发电系统、热电联产等设备热量分析中也有着重要的作用。

辐射传热公式

辐射传热公式

辐射传热公式
辐射传热公式可以使用斯特藩-玻尔兹曼定律来表示。

根据该定律，辐射传热的速率与物体的表面积、物体的发射率以及物体的温度的四次方成正比。

辐射传热公式可表示如下：
Q = εσA(T^4)
其中，Q是辐射传热速率（单位为瓦特或焦耳/秒），ε是物体的发射率（无单位，范围在0到1之间），σ是斯特藩-玻尔兹曼常数（约为5.67 × 10^(-8) W/(m^2·K^4)），A是物体的表面积（单位为平方米），T是物体的温度（单位为开尔文）。

这个公式描述了物体通过辐射传递热量的速率，较高温度的物体会辐射更多的热量。

发射率ε表示了物体有多大比例的辐射能量被传递出去，发射率为1表示物体是完全黑体辐射体，所有的辐射能量都被传递出去。

辐射传热公式可以用于计算太阳辐射、热电厂、电炉等各种热传递问题。

第9章 辐射传热的计算

第9章 辐射传热的计算
ab ac bc 2ab ab bd ad 2ab 2ab
封闭系统 abc ：X ab ,ac
封闭系统 abd ： ab ,bd X 解得： X ab ,cd
bc ad ac bd
X 1, 2
交叉线之和 不交叉线之和 2 表面 A1的断面长度
J1
G1
a
对辐射特性为常数的表面 1 ：
a
J1 E1 1G1
1G1
b
1 E b1
1
b
1 Eb1 1 1 G1
1G1
2. 有效辐射与辐射传热量的关系 从外部： 传热量 q J1 G1 从内部： 传热量 消去 G1 ，并且
J1 G1
a
q 1 Eb1 1G1
9.1.2 角系数的性质 1. 角系数的相对性 （1） 两个微元表面
dA1 和 dA1 （黑体）
2
dA2 对应的立体角：
dAc dA2 cos 2 d 1 2 r r2 dA2 方向可见辐射面积： dA1 cos1
1
X d 1, d 2
落到 dA2上的辐射能 dA1发出的辐射能
A1 X1, 2 J1 J 2
J 1 J 2 ——电势差 1 ——空间热阻 A1 X 1, 2
等效网络图：
1, 2
3. 两个灰体表面组成的封闭系统
1, 2
E b1 E b 2 1 1 1 1 2 1 A1 A1 X 1, 2 2 A2
Z X 1.33 ， Y X Nhomakorabea.67X 2,(1 A) 0.15
③ 由可加性：
X 2,1 A X 2,1 X 2, A X 2,1 X 2,1 A X 2, A 0.05

辐射传热的计算

辐射传热的计算
当没有遮热板时，两块平壁间的辐射换热量：
Q12
A(Eb1Eb2)A T14T24
1112 1
21
在两块平壁之间加一块大小一样、表面发射率相同的遮热板 （忽略导热热阻）
辐射换热量减少为原来的 1/2，即：
112
1 2
12
A 3X 3,1A 3X 3,2A 3
根据角系数的相对性有：
A1X1,2A2X2,1
A1X1,3A3X3,1 A2X2,3A3X3,2
三个非凹表面组成的封闭辐射系统
X1
2
A1
A2 A3 2A1
X1,3
A1
A3 A2 2A1
X2,3
A2
A3 A1 2A2
黑体间的辐射换热及角系数例题讲解：
[例] 试用代数法确定如图所示
的辐射和吸收是在整个气体容积中进行的，属 于体积辐射。
(4) 气体的反射率为零
气体辐射的特点1：
在工业上常见的温度范围内，单原子气体 及空气、H2、O2、N2等结构对称的双原 子气体，无发射和吸收辐射的能力可认为 是透明体。 CO2、H2O、SO2、CH4和CO等气体都具 有辐射的本领。
例：煤和天然气的燃烧产物中常有一定浓度的CO2和
例：大气中的臭氧层能保护人类免受紫外线的伤害
气体辐射的特点3:
热射线穿过气体层时，辐射能沿途被气体 分子吸收而逐渐减弱。其减弱程度取决于 沿途碰到的气体分子数目，碰到的分子数 目越多，被吸收的辐射能也越多。因此气 体的吸收能力αg与热射线经历的行程长 度L，气体分压力p和气体温度Tg等因素有 关。
9.5 辐射传热的控制（强化与削弱）
遮热板的应用:
在现代隔热保温技术中，遮热板的应用 比较广泛。例如：

传热学V4-第九章-辐射传热的计算1

传热学V4-第九章-辐射传热的计算1

传热学 Heat Transfer
Shanghai Jiao Tong University
9-1 角系数的定义、性质与计算 角系数的性质 相对性
1
完整性
可加性
角系数的相对性：
两个表面间的角系数 X1,2和X2,1 不是独立存在的。
（推导基于立体角概念和兰贝特定律）
两个有限大小表面
A1 X 1, 2 A2 X 2,1
2
代数分析法
几何分析法、蒙特卡罗法…
代数分析法： 利用角系数的性质，通过求解代数方程组获得角系数的方法。
X1,2
A1 A2 A3 2 A1
以线段长度表示
X1,2
三个非凹表面组成的封闭系统
l1 l2 l3 2l1
SJTU-OYH
（忽略垂直方向两端辐射能的逸出）
传热学 Heat Transfer
三个漫灰面组成的封闭空腔
SJTU-OYH
传热学 Heat Transfer
Shanghai Jiao Tong University
9-3 多表面系统辐射换热的计算 网络法求解辐射换热的步骤： 3. 根据等效网络图，利用电路基尔霍夫定律（所有流向节点J的热流量代数和＝0），
列出节点的电流（热流量）方程；
X1, 2 X1, 2 A X1, 2 B
X 2,1 A2 A A X 2 A,1 2 B X 2 B ,1 A2 A2
角系数的直接相加仅适合角系数符号第二角码
SJTU-OYH
表面2到表面1
注意：
X 2,1 X 2 A,1 X 2 B,1
传热学 Heat Transfer
Shanghai Jiao Tong University

辐射传热的计算

辐射传热的计算

X ab ,cd
(bc ad ) (ac bd ) 2ab
我们可以归纳出如下的一般关系：
ห้องสมุดไป่ตู้
X 1, 2
交叉线之和 不交叉线之和 2 表面A1的断面长度
图6 两个表面间的角系数
对于在一个方向上长度无限延伸的多个 表面组成的系统，该式为任意两个表面 之间的角系数的计算式，因此该方法又 称为交叉线法。
1. 二灰表面间的辐射换热
R1
1 1 A1 1
Rk
1 A1 X 1, 2
R2
1, 2
Eb1 Eb 2 1 1 1 1 2 A11 A1 X 1, 2 A2 2
2. 三灰表面间的辐射换热
应用电学中的基尔霍夫定律， 可列出节点的热流方程：
J1 :
Eb1 J1 J 2 J1 J 3 J1 0 1 1 1 1 1 A1 A1 X 1, 2 A1 X 1,3
i 1
此式表达的关系称为角系数的完整性。
图3 角系数的完整性
3. 角系数的可加性： 考虑如图4所示表面1对表面2的角系数。由于从表面1上发出而落到表 面2上的总能量，等于落到表面2上各部分的辐射能之和，于是有：
A1Eb1 X1, 2 A1Eb1 X1,2a A1Eb1 X1, 2b
故有 X1,2 X1,2a X1,2b 由于从表面2发出落到表面1上的总 辐射能，等于从表面2的各个组成部 分发出而落到表面1上的辐射能之和。 于是有：
9-1 辐射传热的角系数
一、定义
1.两个假定：1）所研究的表面是漫射的；2）在所研究表面的不同地点上 向外发射的辐射热流密度时均匀的。 * 两个表面之间的辐射换热量与两个表面之间的相对位置有很大关系．图 1示出了两个等温表面间的两种极端布置情况：图a中两表间无限接近， 相互间的换热量最大；图b中两表面位于同一表面上，相互间的辐射换 热量为零。由图可以看出，两个表面间的相对位置不同时，一个表面发 出而落到另一个表面上的 辐射能的百分数随之而异，从而 影响到换热量。 2.定义：我们把表面1发出的辐射能 中落到表面2上的百分数 称为表面1对表面2的角系数， 记为 X1, 2。同理也可以定义表面2 对表面l的角系数。 图1 表面相对位置的影响

辐射传热计算公式

辐射传热计算公式

辐射传热计算公式辐射传热是物体表面和另一物体间传热机制中最重要的类型，它涉及传热过程中表面物体间的能量交换。

传热公式是用来描述表面物体及其交换质量之间能量交换关系的公式，通常被用于辐射对流复合传热中计算传热量的公式。

辐射传热计算公式的基本原理是表面物体之间的能量交换。

它的计算公式可以分为两部分：一部分是用来计算物体表面辐射热传递系数，指出从物体表面向外传递的热量；另一部分是用来计算对流热传递系数，指出物体表面周围的气体和其它物体的热量交换情况。

辐射传热计算公式的具体表达式是：Q=εσAT(T1^4-T2^4)式中：Q表示物体表面之间散热量，单位为W；ε表示物体表面辐射热传递系数；σ表示摩尔辐射常数，单位是W/m^2K^4；A表示物体表面面积；T1和T2分别表示表面物体两端温度，单位是K。

由于物体表面辐射热传递系数ε和对流热传递系数α之间比例关系的存在，因此在辐射对流复合传热过程中，计算传热量的公式为： Q=αAT（T1-T2）式中：Q表示物体表面之间散热量，单位为W；α表示物体表面对流热传递系数；A表示物体表面面积；T1和T2分别表示表面物体两端温度，单位是K。

从上面所介绍的两个传热公式可以看出，计算传热量时，要根据传热的机制，准确的计算物体表面的辐射热传递系数ε和对流热传递系数α以及物体表面面积A，物体表面两端温度T1和T2之间的差值，才能准确的计算出传热量。

计算传热量公式的正确应用可以用于提高物体表面的温度，降低物体表面的温度，改善传热效率，提高设备性能，确定加热器或冷却器的设计参数等。

因此，辐射传热计算公式对于机械工程、热能工程等领域有着重要的意义。

因此，在实际应用中，要根据不同情况，选择合适的传热公式来计算，以确保传热仿真的准确性和可靠性。

此外，还要注意表面物体的性质，如比热容、热导率等，只有正确的参数，才能确保仿真计算结果。

综上所述，辐射传热计算公式对于物体表面间的能量交换机制的研究具有重要的意义，它涉及表面物体间的辐射热传递系数、对流热传递系数、物体表面面积、温度等重要参数，这些参数的准确计算才能保证传热仿真的准确性与可靠性，从而可以实现物体表面的温度控制，提高物体表面的温度控制效果，为机械工程、热能工程的发展做出贡献。

.辐射传热计算

.辐射传热计算

3 A3
A1 X1,3 A2 X 2,3
➢求解节点方程组，获得J1,J2…JN 。
➢净辐射传热量的计算
•表面净辐射热流量：
i
Ebi Ji
1i
n
i, j
i 1
Ai i
•表面间辐射热流量：
i，j
Ji
J 1
j
Ai X i, j
9.3.3 三表面封闭系统特殊情形
➢ 有一表面为黑体表面
表面热阻（1-）/ A=0→J=Eb.。则等效网络图为：
• 两块尺寸为1m×2m、间距为1m的平行平板置于室温 为27℃的大厂房内，平板背面不参与换热。已知两板 的温度分别为t1=827℃， t2=327℃和1=0.2， 2=0.5 。 计算每板的净辐射换热量及厂房壁所得到的辐射热量。
节点代数方程简化为二元方程组。
➢有一个表面为重辐射表面 • q=0→J=Eb。 • 等效网络图为
• J3=Eb3是浮动电势，表面温度未知，取决于J1，J2与J1、 J3和J1、J3间两表面热阻。
• 对于重辐射表面，其网络图可改述为
• 则其余两表面间净辐射换热量1,2可表述为
1，2
Eb1 Eb2 Rt
通过求解封闭的方程组，可得所有角系数，如X1,2为:
X 1, 2
A1 A2 A3 2 A1
l1 l2 l3 2l1
➢计算实例2 求两个非凹无限长相对放置的表面间的角系数。
作辅助假想平面ab,cd,ca,db.
根据角系数的完整性得:
X ab,cd 1 X ab,bd X ab,ac
并有
对于辐射绝热表面
Φ
Eb J
1
0，
J
Eb
A
这种表面称为重辐射面，其具有两重性：

第9章 辐射传热的计算(杨世铭,陶文栓,传热学,第四版,答案)

第9章 辐射传热的计算(杨世铭,陶文栓,传热学,第四版,答案)

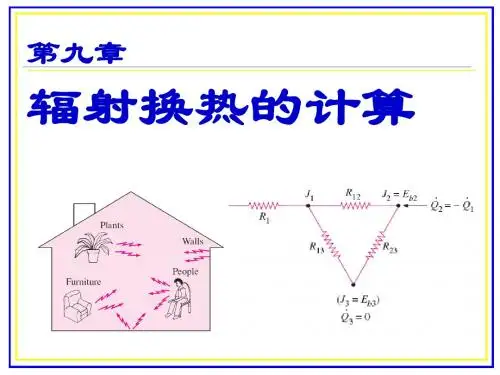
第9章 辐射传热的计算课堂讲解课后作业【9-6】试用简捷方法确定本题附图中的角系数X 1,2。

【解】 (1) 由于121=X ，1,222,11X A X A =0.42443424321211,222,1==⨯⨯⨯===ππl R l R A A A X A X(2) 由于121=X ，1,222,11X A X A =0.5212221211,222,1=====R R A A A X A X ππ (3) 根据(2)的结论，由于对称性125.00.5412,1=⨯=X(4) 假设球的顶部有一块无限大的平板存在，由于对称性0.52,1=X【9-8】已知：如图a 、b 。

求：角系数。

【解】(a) A,2A B A,A 1,21B 1,12B A,1A 1X A X A X A X A X A +++=+++由于对称性，则()1,21B 1,11,21B 1,12B A,1A 1222X A X A X A X A X A +=+=+++。

1A 12A A =+ ，1,2B 1,2B A,1X X X +=∴++B 1,2B A,11,2X X X -=++X =1，Y =2175.01,2=X(b) 扩充图(b)，得1'由扩充图可知，2.021,='X ，由于对称性，可得：05.042.04121,1,2==='X X 1,222,11X A X A =2.005.041,21211,222,1=⨯===X A A A X A X【9-18】一管状电加热器内表面温度为900K 、ε=1，试计算从加热表面投入到圆盘上的总辐射能（见附图）。

【解】表面2发出而落到表面1上的辐射能应为2,11b 1X E A =Φ； 按角系数的对称性，1,222,11X A X A =；做虚拟表面3及4，则可有4,21,23,2X X X +=，即4,23,21,2X X X -=，其中3,2X ，4,2X 为两平行圆盘间辐射角系数。

辐射传热的计算

辐射传热的计算

两微元表面角系数相对性：
dA X1 dA1,dA2 dA2 X dA2 ,dA1

cos1
cos2dA1dA2 r2
长江大学机械工程学院
School of Mechanical Engineering
dA1 两微元面间的辐射
二、角系数的性质
(2) 面对面的角系数
X dA cosr cos dA2,dA1
§ 9-1 角 系 数
一、角系数的定义 二、角系数的性质 三、角系数的计算方法
一、角系数的定义
长江大学机械工程学院
School of Mechanical Engineering
假定：所研究的表面是漫射的；所研究表面的不同 点向外发射的辐射热流密度均匀。
T1
T1
T2
(a)
T2
(b)
定义：把表面1发出的辐射能中落到表面2上的百
二、角系数的性质

A1A2 A1
1、相对性 2、完整性 3、可加性
A1 X1,2 A2 X 2,1
n
X1,i 1
i 1
n
X 1,2 X 1,2i i 1
X 2,1

X 2a,1
A2a A2

X 2b,1
A2b A2
长江大学机械工程学院
School of Mechanical Engineering
长江大学机械工程学院
A A A 1 Schoo2l of Mechan3ical Engineering X 1,2
2 A1
X 1,3

A1 A3 2 A1
A2
X 2,1 X 2,3 1 X 3,1 X 3,2 1

9简单辐射传热计算

9简单辐射传热计算
11
（1）单位面积上表面1、2间的辐射传 热量为
q1,2
11
Eb1
Eb2
1 12
5.67 1 08[2 (12 7217) 43 1(12727)43 ]= 660.7 W/m2
1 X1,2 2
0.6 0.4
（2）表面1的有效辐射
J1
Eb1
111
q1,2
5 .6 7 1 8 0 (22 27)7 4 3 1 0 .6 6.6 70 0 .6
解：对流散热量为
qchd(twtf) 3 .7 3 .1 0 4 .3 ( 64 2 0 0 )83.7W/m
辐射散热量为
qr1A 1 (T 14T 2 4)
0 . 5 3 . 1 0 . 3 4 5 . 6 6 1 - 8 7 ( 0 2 4 4 - ( 7 0 2 0 ) 4 3 ) 73
（2）角系数的完整性
n
X1,1 X1,2 X1,3 X1,n x1,i 1
（3）角系数的可加性
i1
X1,2 X1,2a X1,2b
3
3、角系数的确定方法
（1）定义法
（2）代数分析法
由角系数的相对性得
X1,2
A2 A1
X2,1
1 2
由角系数的完整性得
1
X1,1
1X1,2
2
1
X 2,1 1
2
X1,2 ?
X1,1 ?
4
二、有效辐射
1、定义
有效辐射是指单位时间内离开物体单位表面积的辐射能，用符号J表示, 单位为W/m2。
J1 E1 1G1 1Eb1 (11)G1
2、单位时间内的辐射散热量
与有效辐射J 之间的关系：

辐射传热

辐射传热

二、物体的辐射能力
物体辐射的能力：是指物体在一定温度下，单位表面积、 物体辐射的能力：是指物体在一定温度下，单位表面积、 单位时间内所发射的全部波长的总能量， 表示， 单位时间内所发射的全部波长的总能量，用E表示，单位 表示 W/m2，因此，辐射能力表征物体发射辐射能的本领。 因此，辐射能力表征物体发射辐射能的本领。
4
4
通常将灰体的辐射能力与同温度下黑体的辐射能力之 比定义为物体黑度， 表示。 比定义为物体黑度，用ε表示。 不同物体的C值不同，其值与物体的性质、 不同物体的 值不同，其值与物体的性质、表面状况 值不同 和温度有关，但恒小于C 。 和温度有关，但恒小于 0。
3 克希霍夫定律
对灰体
Q = E − AE b
T1> T2
得
平行平板间辐射传热
结论： 结论：
能力与吸收率的比值均相同， （1）任何物体的辐射能力与吸收率的比值均相同，恒等 ）任何物体的辐射能力与吸收率的比值均相同 同温度下绝对黑体的发射能力 发射能力， 于同温度下绝对黑体的发射能力，且只与物体的绝对温度 有关。物体的发射能力越强 其吸收率越大。 的发射能力越强， 有关。物体的发射能力越强，其吸收率越大。 （2）A=ε 即同温度下，物体的吸收率与黑度在数值上 ） ε 即同温度下， 相等，但物理意义不同。 相等，但物理意义不同。
设备中热损失计算
有保温层的设备外壁与周围环境的联合传热 系数， 系数，可用下列各式进行计算
2
c1 = 3.743 × 10−16 W ⋅ m2 c2 = 1.4387 × 10−2 m ⋅ K
描述黑体的单色辐射能力, 描述黑体的单色辐射能力 揭示了黑体辐射能力按照 波长的分配规律. 波长的分配规律 根据上式描绘的黑体光谱辐射力 随波长和温度的依变关系。 随波长和温度的依变关系。 Wien位移定律 λm与 的关系由Wien λm与T 的关系由Wien位移定律 给出:

辐射传热的计算

辐射传热的计算
两个任意放置的灰表面间的辐射传热量为：
1,2 J1 A1 X1,2 - J 2 A2 X 2,1
1,2 A1 X1,2 J1 - J 2 =A2 X 2,1 J1 - J 2
J1 J 2 J1 J 2 1,2 1 A1 X 1,2 1 A2 X 2,1
类似于欧姆定律，满足势差、阻力和流的关系
A1 X12 =A2 X 21
b(12) A 1 X12 Eb1 Eb2 =A 2 X 21 Eb1 Eb2
第9章 辐射传热的计算
9.1 辐射传热的角系数/角系数的性质

性质2：角系数的完整性
X i ,1 X i ,2
X i ,n
= X i , j
X 1,2
ad bc ac bd
2ab
X 1,2

交叉线长度之和 非交叉线长度之和 2倍表面 1的横断面线段长度
——交叉线法
第9章 辐射传热的计算
9.1 辐射传热的角系数/角系数的计算
第9章 辐射传热的计算
9.2 两表面封闭系统的辐射传热/封闭腔模型

两个黑体表面之间的净换热量

对只有两个黑体表面换热的封闭系统，二者一致 对任意位置的两个表面，二者不相等

“半球空间”概念的引入 “封闭腔模型”的重要性
第9章 辐射传热的计算
9.2 两表面封闭系统的辐射传热/封闭腔模型

封闭腔应包括的表面： ——能接受研究表面发射的 辐射能的其他所有表面

——能将辐射能投射到研究

X12

离开表面1并投落到表面2上的辐射能 离开表面1的总辐射能
同样可定义X2,1

辐射传热的计算

辐射传热的计算

两特殊情形：a）一表面为黑体。 1 1 1 A1 X 1, 2 E A1 1 J
b1 1
长江大学机械工程学院
School of Mechanical Engineering
J2
1 A2 X 2 ,3
1 2 A2 2
Eb2
1 A1 X 1,3
J3= Eb3
表面3为黑体 节点1： 节点2：
四、气体的发射率εg和吸收比αg
五、气体与包壁的辐射传热
长江大学机械工程学院
School of Mechanical Engineering
例2：在太阳系中，地球和火星距太阳的距离相 差不大，但为什么火星表面温度昼夜变化却比 地球要大得多？
长江大学机械工程学院
School of Mechanical Engineering
解：未加入遮热板前：
1 1 1 s 1 1 1 1 2.75 1 1 1 2 0.4 0.8
1 0.4 2 0.8
0.04
加遮热板后：
s
1 1 1 1 1 1 1 51.75 0.4 0.04 0.04 0.8 1
辐射换热降低的百分率： 1 1 s s 2.75 51.75 100 % 94.7% 1 s 2.75
为0.04，求由此引起的辐射换热降低的百分率。
1, 2
0 AT T 1 1 1 2 1
4 1 4 2
1 0.4 2 0.8
0.04
¢ F 1,2 =
s 0A T 14 - T 24
(
)
1 e1 + 2 e3 + 1 e2 - 2
长江大学机械工程学院
School of Mechanical Engineering

传热学-辐射传热的计算

传热学-辐射传热的计算

X1,2
=
A1 + A2 − 2A1
A3
X1,3
=
A1 + A3 − 2A1
A2
X 2,3
=
A2
+ A3 − 2A2
A1
相对性
A1 X1,2 = A2 X 2,1 A1 X1,3 = A3 X 3,1 A2 X 2,3 = A3 X 3,2
三个非凹表面组成的封闭系统
由于垂直纸面方向的长度相同，则有：
微元面积 d A1 对 A2的角系数为
∫ X d1，2 =
cosθ1 cosθ2dA2
A2
πr2
A1对 A2 的角系数为
∫ ∫ A1X1，2 =
⎛ A1 ⎜⎝
A2
cosθ1 cosθ2dA2 πr2
⎞⎟⎠dA1
∫ ∫ X1，2
=
1 A1
A1
cosθ1 cosθ2dA2dA1
A2
πr2
这就是求解任意两表面之间角系数的积分表达式。注意这是一个四重积 分，不少情况下会遇到一些数学上的因难，需采用某些专门的技巧
¾ 本节所讨论的固体表面间的辐射换热是指表面之间不存在参 与热辐射介质的情形
¾ 本节将给出两个稳态辐射换热的例子，即分别由等温的两黑 体或等温的两漫灰体组成的封闭系统内的表面间辐射换热
¾ 封闭系统内充满不吸收任何辐射的透明介质 ¾ 所采用的方法称为“净热量”法
9.2.1 两黑体表面组成的封闭腔的辐射传热
X1,2 = X1,2a + X1,2b n
∑ 如把表面2进一步分成若干小块，则有 X1,2 = X1,2i i =1
从表面2上发出而落到表面1上的辐射能，等于从表面2的各部分发 出而落到表面1上的辐射能之和，于是有
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

（2）角系数的完整性
n
X1,1 X1,2 X1,3 X1,n x1,i 1
（3）角系数的可加性
i1
X1,2 X1,2a X1,2b
3、角系数的确定方法
（1）定义法 （2）代数分析法
由角系数的相对性得
X 1, 2
A2 A1
X 2,1
1 2
由角系数的完整性得
1 X1,1 1 X1,2 2
练习
1. 用裸露的热电偶测量管道中气体的温度，稳定后，热电偶所指示的温度为175 ℃。 已 知 管 道 内 壁 温 度 为 90 ℃ ， 高 温 气 流 与 热 电 偶 结 点 的 表 面 传 热 系 数 为 320 W/ （m2·K），热电偶结点的表面发射率为0.6。试求高温气体的真实温度。
2. 由两个可以认为是无限长同心圆柱组成的空腔系统，圆柱1外径为60mm，圆柱2内 径为90mm。表面1温度为127℃，表面2温度为57℃。试计算以下两种情况下两表面 间单位长度上的辐射传热量：（1）表面1和2均近似作为黑体表面；（2）表面1和表 面2为发射率分别为0.8和0.6的漫灰表面。
5.67 108 (227 273)4 1 0.6 660.7 0.6
= 3103.3 W/m2
例题2 有一水平放置于室内的蒸汽管道，其保温层的外径d=360mm，正常情况下， 保温层表面的温度为40℃ ，室内空气与保温层外壁的对流传热表面传热系 数为3.7W/(m2.K)，室内的空气温度和房间壁面的温度均为20℃ ，保温层外 表面的发射率为0.5。试计算每米管长上的散热量。
1
X2,1 1
2
X1,2 ?
X1,1 ?
二、有效辐射
1、定义
有效辐射是指单位时间内离开物体单位表面积的辐射能，用符号J表示, 单位为W/m2。
J1 E1 1G1 1Eb1 (11)G1
2、单位时间内的辐射散热量
与有效辐射J 之间的关系：
1
(J1
G1 ) A1
Eb1 J1
1 1
A11
三、两个表面的辐射传热
解：对流散热量为
qc hd(tw tf ) 3.73.140.36(40 20) 83.7W/m
辐射散热量为
qr 1A1 (T14 T24 )
0.53.14 0.36 5.67 10-8 (273 40) 4 - (273 20)4
71.4W/m
总散热量为
q qc qr 83.7 71.4 155.1W/m
传热学
简单辐射传热 分析与计算
一、角系数
1、定义
我们把从表面1发出的辐射能中落到 表面2上的份额,称为表面1对表面2的 角系数, 记为X1,2 。
表面1
表面2
X1,2 = X2, 1 =1
X1,2 = X2, 1 =0
角系数是纯几何因子。 0 ≤ X1,2 ≤ 1
2、性质
A X A X （1）角系数的相对性 1 1,2 2 2,1
两个表面构成封闭系统；
两个表面都是漫射的灰表面， 简称漫灰表面；
ห้องสมุดไป่ตู้
封闭系统中的介质是透热的， 即不参与辐射和吸收。
任意两个表面的辐射传热量可表示成：
1,2 A1J1X1,2 A2J2 X 2,1 A1X1,2(J1 J2 )
表面1的辐射散热
表面2的辐射吸热
1
Eb1 J1
1 1
A11
2
J2 Eb2
12
A2 2
1,2 1 2
表面1和2之间的辐射传热量为
1,2
1
1
Eb1
1
Eb2
1
2
A11 A1X1,2 A22
表面辐射热阻
Eb J
1
A
空间辐射热阻
1,2 A1X1,2 (J1 J2 ) J1 J2 1 A1 X 1,2
1,2
1
1
Eb1
1
Eb2
1
2
A11 A1X1,2 A22
特别的，对于大空间包小物体情况
1,2
1
1
Eb1
1
Eb2
1
2
A11 A1X1,2 A22
X1,2 1 A1 A2
单位时间内，小物体与大空间的辐射传热量为
例题1 附图中所示的是两个无限靠近的平行大表面，已知表面1 的温度为227℃，发射率为0.6，表面2的温度为127℃，发 射率为0.4。试计算： （1）单位面积上表面1、2间的辐射传热量； （2）表面1的有效辐射。
解：首先画出示意图并 对该问题进行分析
管道的散热量包括 对流散热和辐射散热
其保温层的外径d=360mm，保温层表面的温度为40 ℃ ，室内空气与保温层外壁的对 流传热表面传热系数为3.7W/(m2.K)，室内的空气温度和房间壁面的温度均为20 ℃ ， 保温层外表面的发射率为0.5。试计算每米管长上的散热量。
解：首先画出辐射热网络图
（1）单位面积上表面1、2间的辐射传 热量为
q1,2
1
1
Eb1
1
Eb2 1
2
5.67108 [(227 273)4 (127 273)4] = 660.7 W/m2 1 1 1
1 X1,2 2
0.6 0.4
（2）表面1的有效辐射
J1
Eb1
1 1 1
q1,2
3. 一黑体炉，其圆柱形炉腔的直径为d = 10cm、深度为l = 40cm , 炉腔内壁面发射率 为 = 0.9 ，炉内温度为927℃，室内壁面温度为27℃。试计算炉门打开时，单位时间 内通过炉门与环境的辐射传热量。
再见！