下载文档原格式
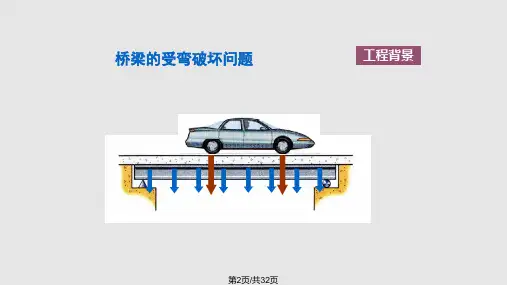
伸缩臂的弯曲应力计算公式伸缩臂是一种常见的机械设备，其主要功能是在需要时伸展或收缩，从而完成特定的工作任务。
在伸缩臂的设计和制造过程中，需要考虑到其受力情况，特别是在弯曲状态下所受到的应力。
弯曲应力是指在材料受到外部力作用下，其内部产生的应力状态。
本文将介绍伸缩臂的弯曲应力计算公式及其应用。
伸缩臂的弯曲应力计算公式可以通过梁的弯曲理论来推导。
在伸缩臂的设计中，常常需要考虑到其所承受的最大弯曲应力，以确保其在工作过程中不会发生破坏。
梁的弯曲理论是基于梁的几何形状和材料性质来推导出梁在受力状态下的应力分布。
根据梁的弯曲理论，伸缩臂的弯曲应力计算公式可以表示为：σ = M c / I。
其中，σ表示梁的弯曲应力，单位为N/m^2；M表示梁的弯矩，单位为N·m；c表示梁的截面到受力点的距离，单位为m；I表示梁的惯性矩，单位为m^4。
在伸缩臂的设计中，需要根据实际情况来确定梁的弯矩、截面到受力点的距离和惯性矩。
弯矩是指在梁上受到的外部力矩，其大小与梁的几何形状和受力情况有关。
截面到受力点的距离是指在梁的截面上受力点到该截面的距离，其大小取决于梁的几何形状。
惯性矩是指梁在受力方向上的惯性矩，其大小与梁的截面形状和尺寸有关。
在实际工程中，伸缩臂的弯曲应力计算公式可以通过有限元分析等方法来进行验证和优化。
有限元分析是一种常用的工程分析方法，通过将复杂的结构分解为有限个简单的单元，然后利用数值方法求解出整个结构的受力和变形情况。
通过有限元分析，可以得到伸缩臂在受力状态下的弯曲应力分布，从而对其设计进行优化和改进。
伸缩臂的弯曲应力计算公式在工程实践中具有重要的意义。
通过对伸缩臂的弯曲应力进行计算和分析，可以有效地指导其设计和制造过程，确保其在工作过程中不会发生破坏。
同时，通过对伸缩臂的弯曲应力进行优化，可以提高其承载能力和使用寿命，从而提高整个机械设备的性能和可靠性。
总之，伸缩臂的弯曲应力计算公式是伸缩臂设计和制造过程中的重要内容。
如何计算物体的弯曲应力和应变？
要计算物体的弯曲应力和应变，首先需要了解一些基本概念和公式。
以下是一些可能有用的信息：
1. 弯曲应力：当物体受到外力作用时，它会在力的方向上产生弯曲。
这种弯曲会导致物体内部产生应力，称为弯曲应力。
弯曲应力的大小取决于外力的大小、物体的截面尺寸和材料性质等因素。
计算弯曲应力的公式为：σ= F/A，其中σ为弯曲应力，F为作用在物体上的外力，A为物体的截面面积。
2. 应变：当物体受到外力作用时，它会在力的方向上产生变形。
这种变形会导致物体内部产生应变。
应变的大小取决于外力的大小、物体的尺寸和材料性质等因素。
计算应变的公式为：ε= ΔL/L，其中ε为应变，ΔL为物体的变形量，L为物体原来的长度。
在实际应用中，为了更准确地计算弯曲应力和应变，需要考虑更多的因素，例如物体的形状、材料性质、温度等。
同时，还需要进行实验测试和有限元分析等方法来验证计算结果的准确性。
