下载文档原格式
悬臂梁受集中载荷的应力变形计算悬臂梁是一种常见的结构，在工程中应用广泛。
在设计和分析悬臂梁时，经常需要计算受集中载荷作用下的应力和变形。
本文将对悬臂梁受集中载荷的应力和变形计算进行详细阐述。
一、悬臂梁受集中载荷的应力计算1.弯曲应力计算当悬臂梁受到集中荷载作用时，会产生弯曲应力。
弯曲应力是由于载荷作用引起梁的弯曲变形而产生的。
计算弯曲应力可使用弯曲应力公式：σ=(M*y)/I其中，σ为弯曲应力，M为弯矩，y为弦纤维上离中轴线的距离，I 为截面转动惯量。
在悬臂梁上的集中荷载作用下，弯矩可通过以下公式计算：M=F*L其中，M为弯矩，F为集中荷载，L为悬臂梁的长度。
对于矩形截面的悬臂梁，截面转动惯量I可通过以下公式计算：I=(b*h^3)/12其中，I为截面转动惯量，b为矩形截面的宽度，h为矩形截面的高度。
2.剪切应力计算除了弯曲应力外，悬臂梁还会受到剪切应力的作用。
剪切应力是指梁截面内部不同层次之间的相对滑动所产生的应力。
计算剪切应力可使用剪切应力公式：τ=(V*Q)/(b*I)其中，τ为剪切应力，V为剪力，Q为梁截面的截面模量，b为截面的宽度，I为截面转动惯量。
悬臂梁上的剪力可通过以下公式计算：V=F其中，V为剪力，F为集中荷载。
悬臂梁的截面模量Q可通过以下公式计算：Q=(b*h^2)/6其中，Q为截面模量，b为截面的宽度，h为截面的高度。
二、悬臂梁受集中载荷的变形计算1.弯曲变形计算悬臂梁受到集中载荷作用时，会产生弯曲变形。
弯曲变形是指悬臂梁由于受到集中载荷作用发生的弯曲现象。
计算弯曲变形可使用弯曲变形公式：δ=(M*L^2)/(2*E*I)其中，δ为弯曲变形，M为弯矩，L为悬臂梁的长度，E为弹性模量，I为截面转动惯量。
2.剪切变形计算悬臂梁除了弯曲变形外，还会受到剪切变形的作用。
剪切变形是指梁截面内部不同层次之间的相对滑动所产生的变形。
计算剪切变形可使用剪切变形公式：θ=(V*L)/(G*Q)其中，θ为剪切变形，V为剪力，L为悬臂梁的长度，G为剪切模量，Q为截面模量。
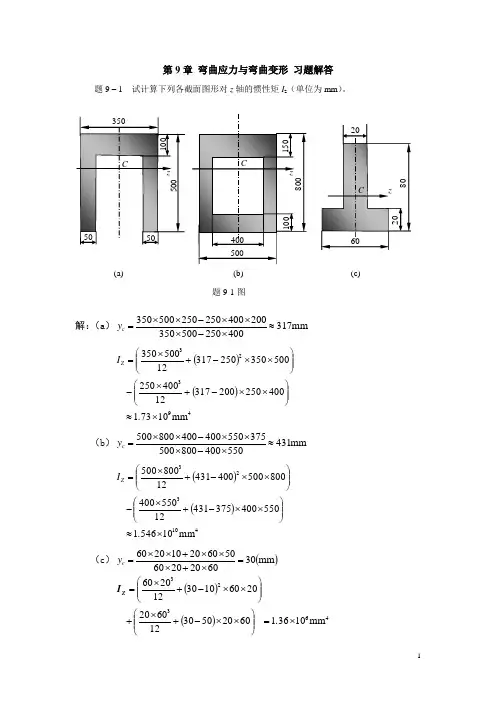
第9章 弯曲应力与弯曲变形 习题解答题9 – 1 试计算下列各截面图形对z 轴的惯性矩I z （单位为mm ）。
解：（a ）mm 317400250500350200400250250500350≈⨯-⨯⨯⨯-⨯⨯=c y()()49323mm 107314002502003171240025050035025031712500350⨯≈⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.I Z （b ）mm 431550400800500375550400400800500≈⨯-⨯⨯⨯-⨯⨯=c y()()410323mm 1054615504003754311255040080050040043112800500⨯≈⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.I Z （c ）()mm 3060202060506020102060=⨯+⨯⨯⨯+⨯⨯=c y()()46323mm103616020503012602020601030122060⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯+⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.Z I(a)(b) (c)题9-1图题9–2 悬臂梁受力及截面尺寸如图所示。
设q = 60kN/m ，F = 100kN 。
试求（1）梁1– 1截面上A 、B 两点的正应力。
（2）整个梁横截面上的最大正应力和最大切应力。
解：（1）求支反力kN 220100260=+⨯=A F （↑）m kN 32021001260⋅=⨯+⨯⨯=A M （ ） （2）画F S 、M 图（3）求1-1截面上A 、B 两点的正应力 m kN 1305016011001⋅=⨯⨯+⨯=.MF MA 点：MPa 254Pa 1025412150100550101306331=⨯≈⨯⨯⨯==...I y M zA t σB 点：MPa 162Pa 107816112150100*********331=⨯≈⨯⨯⨯==....I y M σzB c （4）求最大正应力和最大切应力M P a 853Pa 10385361501010320623max max =⨯≈⨯⨯==...W M σzM P a 22Pa 10221501010220232363max =⨯≈⨯⨯⋅=⋅=..A F τS 题9 - 3 简支梁受力如图所示。
工程力学中的弯曲应力和弯曲变形问题的探究与解决方案引言：工程力学是研究物体受力和变形规律的学科，其中弯曲应力和弯曲变形问题是工程力学中的重要内容。
本文将探讨弯曲应力和弯曲变形问题的原因、计算方法以及解决方案，旨在帮助读者更好地理解和应对这一问题。
一、弯曲应力的原因在工程实践中，当梁、梁柱等结构承受外力作用时，由于结构的几何形状和材料的力学性质不同，会导致结构发生弯曲变形。
弯曲应力的产生主要有以下几个原因：1. 外力作用：外力作用是导致结构弯曲的主要原因之一。
例如，悬臂梁受到集中力的作用，会导致梁的一侧拉伸，另一侧压缩，从而产生弯曲应力。
2. 结构几何形状：结构的几何形状对弯曲应力有直接影响。
例如，梁的截面形状不均匀或不对称，会导致弯曲应力的分布不均匀，从而引起结构的弯曲变形。
3. 材料力学性质：材料的力学性质也是导致弯曲应力的重要因素。
不同材料的弹性模量、屈服强度等参数不同，会导致结构在受力时产生不同的弯曲应力。
二、弯曲应力的计算方法为了准确计算弯曲应力，工程力学中提出了一系列的计算方法。
其中最常用的方法是梁的弯曲方程和梁的截面应力分析。
1. 梁的弯曲方程：梁的弯曲方程是描述梁在弯曲过程中受力和变形的重要方程。
根据梁的几何形状和受力情况，可以得到梁的弯曲方程，并通过求解该方程，计算出梁在不同位置的弯曲应力。
2. 梁的截面应力分析：梁的截面应力分析是通过分析梁截面上的应力分布情况，计算出梁在不同位置的弯曲应力。
该方法根据梁的几何形状和材料的力学性质，采用静力学平衡和弹性力学理论，计算出梁截面上的应力分布，并进一步得到梁的弯曲应力。
三、弯曲变形问题的解决方案针对弯曲变形问题，工程力学提出了一系列的解决方案，包括结构改进、材料选择和加固措施等。
1. 结构改进：对于存在弯曲变形问题的结构，可以通过改进结构的几何形状，增加结构的刚度，从而减小结构的弯曲变形。
例如，在梁的设计中，可以增加梁的截面尺寸或改变梁的截面形状，以增加梁的抗弯刚度。
课程: 材料力学教者：第30,31,32课时(3.22,3.26)课程内容或课题：1．梁纯弯曲时横截面上正应力计算公式的推导2．熟练弯曲正应力强度条件的建立和相应的计算目的要求：1．掌握梁纯弯曲时横截面上正应力计算公式的推导过程，理解推导中所作的基本假设2．理解横力弯曲正应力计算仍用纯弯曲公式的条件和近似程度3．掌握弯曲正应力强度条件的建立和相应的计算重点难点：1.纯弯曲梁横截面上正应力公式的分析推导2.横力弯曲横截面上正应力的计算，最大拉应力和最大压应力的计算3.弯曲的强度计算教学形式、手段：采用启发式教学，通过提问，引导学生思考教学过程：一：导入新课二：授新1、几个基本概念⑴平面弯曲和弯曲中心变形后梁轴线的位移方向沿着加载方向的弯曲情况，称为平面弯曲。
图6-1怎样加载才能产生平面弯曲？若梁的横截面有对称平面时，载荷必须作用在次对称平面内，才能发生平面弯曲。
图6-2若梁的横截面没有对称平面时，载荷的作用线必须通过截面的弯曲中心。
什么叫弯曲中心？当载荷的作用线通过横截面上某一点特定点时，杆件只产生弯曲而无扭转。
这样的特定点称为弯曲中心。
图6-3关于弯曲中心位置的确定及工程上常见图形的弯曲中心位置。
图6-4①具有两个对称轴或反对称的截面，如工字形、圆形、圆环形、空心矩形截面等，弯曲中心与形心（两对称轴的交点）重合，如图6-4(a),(b),(c)所示。
②具有一个对称轴的截面，如槽形和T形截面，弯曲中心必在对称轴上，如图6-4(d)、(e)所示。
③如果截面是由中线相交于一点的几个狭长矩形所组成，如L形或T形截面，则此交点就是弯曲中心，如图6-4(e)、(f)④不对称实心截面的弯曲中心靠近形心。
这种截面在荷载作用线通过形心时也将引起扭转，但由于这种截面的抗扭刚度很大，弯曲中心与形心又非常靠近，故通常不考虑它的扭转影响。
⑵纯弯曲和横力弯曲图6-5平面弯曲时，如果某段梁的横截面上只有弯矩而无剪力，这种弯曲称为纯弯曲；如果梁的横截面上既有弯矩又有剪力，则这种弯曲称为横力弯曲。
⑶中性层和中性轴图6-6弯曲时梁内既不伸长又不缩短的一层纤维称为中性层。
中性层与横截面的交线称为中性轴。
注意：中性层是对整个梁而言的；中性轴是对某个横截面而言的。
中性轴通过横截面的形心，是截面的形心主惯性轴。
2、正应力强度计算⑴平面弯曲时，正应力沿截面高度的分布规律，以矩形截面为例，见图6-7，b 所示。
(a) (b)图6-7 ⑵正应力计算公式：y I M Z ⋅=σ ⑴ 式中：y 为所求正应力的点到中性轴的距离；Z I ： 矩形123bh ；圆形644D π ⑶正应力强度条件：][max max max max σσ≤=⋅=ZZ Z Z W M y I M ⑵式中：max y I W Z Z = 矩形62bh W Z = 圆形323bD W Z = 例题6-1 已知钢梁Mpa 160][=σ，试决定I 字钢型号及截面尺寸（自重不计）。
解：作内力图；图6-11 m N ⋅==k ql M 4082max 3663max 10250101601040][m -⨯=⨯⨯==σM W Z 查表采用I20b (3250cm =X W )其截面尺寸见表。
例题6-2 已知铸铁梁的[+σ]=40MPa 、[-σ]=110MPa 、42610cm =Z I ,试校核梁的强度。
解：作内力图：图6-12校核 B 截面；][MPa +--+=⨯⨯⨯⨯=⋅=σσ 8.36102610108.410208231max max y I M Z ][MPa ----=⨯⨯⨯⨯=⋅=σσ 109102610102.1410208232max max y I M Z 问题讨论：如果把梁倒放可以看到该梁就会出现强度不足的情况。
例题6-3 在图6-14所示的结构中，AB 为一铸铁梁，其材料的许用应力为[t σ]=30MPa 、[c σ]=80MPa 。
BC 为一圆截面钢杆，其直径d=20mm 、材料的许用应力为[σ]=160MPa 。
试确定结构的许用荷载[q]。
图6-14解：⑴求BC N F 并作AB 梁的FS 、M 图0=∑A m ，得：q q F NBC 25.225.13=⨯=（拉）作AB 梁的FS 、M 图见上。
⑵截面的几何性质计算：AB 梁的横截面：①计算C y （取1Z 为参考轴，对之取矩）mm 8820120208060201201302080=⨯+⨯⨯⨯+⨯⨯=C y ②计算Zc I ；44m mm 8423231076310763)6088(120201212020)88130(2080122080-⨯=⨯=-⨯⨯+⨯+-⨯⨯+⨯=Zc I BC 杆的横截面面积：222402.04m 103.144-⨯=⨯==ππd A⑶确定结构的许用荷载[q]①由BC 杆的抗拉强度确定[q]=？∵][σσ≤=AF NBC 即KN 2.504102010160][][626=⨯⨯⨯⨯=⋅=-πσA F NBC 又∵q N BC 25.2= ∴m kN 3.2225.22.50][==BC q ②由AB 梁的强度确定[q]=？B 截面：（M=0.52qm ）上边缘：][++≤=σσZI My 1 即：68103010763052.05.0⨯≤⨯⨯-q KN/m 8.8052.05.010*******][86=⨯⨯⨯⨯=-上B q下边缘：][--≤=σσZI My 2即：68108010763088.05.0⨯≤⨯⨯-qKN/m 9.13088.05.010*******][86=⨯⨯⨯⨯=-下B qD 截面：（M=0.2812qm б:上压，下拉） 上边缘：][+-≤=σσZI My 1即：68108010763052.0281.0⨯≤⨯⨯-qKN/m 8.41052.0281.010*******][86=⨯⨯⨯⨯=-上D q 下边缘：][++≤=σσZI My 2即：68103010763088.0281.0⨯≤⨯⨯-qKN/m 25.9088.0281.010*******][86=⨯⨯⨯⨯=-下D q结论：KN/m 8.8][][B ==上q q还有其他例题放在PPT 中来讲。
三．总结本次课内容课程 材料力学 教者： 第33-35课时(3.29)课程内容或课题：1.梁横力弯曲时横截面上的切应力2.提高弯曲强度的若干措施、薄壁杆件的切应力流和弯曲中心目的要求：1.掌握各种形状截面梁（矩形、圆形、圆环形、工字形）横截面上切应力的分布和计算。
2.熟练弯曲正应力和剪应力强度条件的建立和相应的计算。
3.了解什么情况下需要对梁的弯曲切应力进行强度校核。
4.从弯曲强度条件出发，掌握提高弯曲强度的若干措施。
重点难点：弯曲横截面上的剪应力教学形式、手段：采用启发式教学，通过提问，引导学生思考，多媒体教学 教学过程：一：导入新课二：授新3.剪应力强度计算⑴剪应力计算公式：bI S F Z Z Q *=τ ⑶ 式中：***⋅=y A S Z 即*A 对中性轴的静矩（见图6-8）。
⑵工程上常见的几种截面图形的剪应力沿截面高度分布规律近似计算式 ①矩形截面A Q 23max =τ ⑷图6-8②工字形截面：dh F Q1max =τ⑸ 式中：h 1—腹板的高度d —腹板的宽度图6-9③实心圆截面A F Q34max ≈τ ⑹图6-10④空心圆截面AF Q 2max ≈τ ⑺式中：4422d D A ππ-=图6-11⑶剪应力强度条件][maxmax max ττ≤=*bI S F Z Z Q ⑻例题6-4 已知[σ]=160MPa 、[τ]=100Mpa ，试选择适用的工字钢型号。
解：⑴作Fs 、M 图⑵按正应力强度选择 工字钢型号33663max 28110281101601045][cm m =⨯=⨯⨯==-σM W Z 查表：3309cm =X W ，即选用22aI 字钢 ⑶剪应力强度校核 查I x :S x,得cm S I XX9.18=，d=0.75cm 由FS 图知 KN 210max =Q F 代入剪应力强度条件： 图6-13 由此校核可见：m ax τ超过[τ]很多。
应重新设计截面。
⑷按剪应力强度选择I 字钢型号 现以25b 工字钢进行试算。
由表查处：cm 27.21=XXS I ，d=1cm ][MPa ττ 6.981011027.2110210223max =⨯⨯⨯⨯=-- ⑸结论：要同时满足正应力和剪应力强度条件，应选用型号为25b 的工字钢。
4．提高弯曲强度的措施 1）梁的合理受力(降低最大弯矩m axM )(1)合理放置支座(从设计方案考虑)双杠，等强，minmax M M =以剪支梁为例，最大弯矩为82maxql M =若两端支座各向中心移动l 2.0，最大弯矩减小为402maxql M =（2)合理布置载荷(从使用方案考虑)2）合理设计截面形状(增大抗弯截面模量z W ) （1）梁的截面优化W M maxmax =σ ，对于宽b ，高为h 的矩形，抗弯截面模量AhAh W z 167.06== 。
因此，高度越大，z W 越大，max σ越小。
在外边缘达到许用应力时，中性轴附近的应力很小，造成材料的浪费。
例如：圆形截面。
理想的情况是将面积之半分布于距中性轴为2h处。
a.塑性材料[][]c t σσ=上、下对称 抗弯更好，抗扭差。
b.脆性材料[][]c t σσ<采用T 字型或上下不对称的工字型截面。
3）等强度梁-截面沿杆长变化，恰使每个截面上的正应力都等于许用应力，这样的变截面梁称为等强度梁。
由()()[]σσ==x W x M max 得()()[]σx M x W =若图示悬臂梁为等强度梁。
等宽度h ，高度为x 的函数，b=b(x)。
则()Pxx M 21=()()()[][]σσPxx M h x b x W 2162=== 得出()[]x h P x b 23σ=按剪切强度确定截面宽度的最小值m in b 。
[]ττ===h b Ph b Q min min max212323 []τh P b 43min =由于变截面梁并不节省材料，且加工麻烦，因此采用阶梯梁(加工方便)。
三．总结本次课内容课程材料力学教者：第36，37课时(4.2)课程内容或课题：1.弯曲变形的量度及符号规定2.挠曲线近似微分方程及其积分目的要求：1．掌握求梁变形的两种方法：积分法和叠加法重点难点：梁的变形分析、挠曲线近似微分方程、积分法求梁的变形教学形式、手段：采用启发式教学，通过提问，引导学生思考，让学生回答问题教学过程：一：导入新课回顾：弯曲内力——在外力作用下，梁的内力沿轴线的变化规律。
弯曲应力——在外力作用下，梁内应力沿横截面高度的分布规律。
