下载文档原格式
利用Excel进行数据比较与差异分析通过对比数据进行差异分析和发现问题利用Excel进行数据比较与差异分析在数据处理和分析的领域中，Excel是一种广泛使用的工具。
其强大的数据比较和分析功能可帮助我们深入挖掘数据，发现其中的差异并解决问题。
本文将介绍如何利用Excel进行数据比较与差异分析的方法和步骤。
一、数据准备在进行数据比较和差异分析之前，我们首先需要准备好数据。
假设我们有两个数据集A和B，分别表示两个不同时间段或者不同实验条件下的数据。
确保数据集的格式一致，并存储在Excel的不同工作表或者不同的工作簿中。
二、数据比较1. 打开Excel，并在两个数据集的工作表中选择需要进行比较的数据范围。
2. 在主菜单栏中选择“条件格式”，然后选择“新规则”。
3. 从弹出的对话框中选择“使用公式确定哪些单元格要进行格式设置”。
4. 在“格式值”输入框中，输入公式“=A1<>B1”（其中A1和B1为两个数据集中的对应单元格）。
5. 在“设置格式”中选择要应用的格式，可以选择不同的填充颜色来突出显示差异。
6. 单击“确定”按钮，然后将格式应用到整个数据范围。
这样，Excel会根据设定的规则对两个数据集进行比较，并将不同的部分以突出显示的形式展现出来。
三、差异分析数据比较之后，我们可以进一步进行差异分析，以深入了解数据之间的差异并找到问题所在。
1. 使用Excel的数据透视表功能可以帮助我们更好地分析数据差异。
选择两个数据集中的所有数据，并在主菜单栏中选择“插入”-“透视表”。
2. 在弹出的对话框中，选择要分析的数据集范围并确定透视表的位置。
3. 在透视表字段列表中，将需要比较的指标和维度字段拖拽到相应的区域。
4. 使用透视表的行和列字段可以对数据进行分类和分组，从而更好地显示数据之间的差异。
5. 可以利用透视表的值字段选项，选择并应用统计函数，如求和、平均值等，以便对数据进行更详细的分析。
6. 根据透视表的分析结果，我们可以对差异进行深入研究，并找出可能的问题所在。
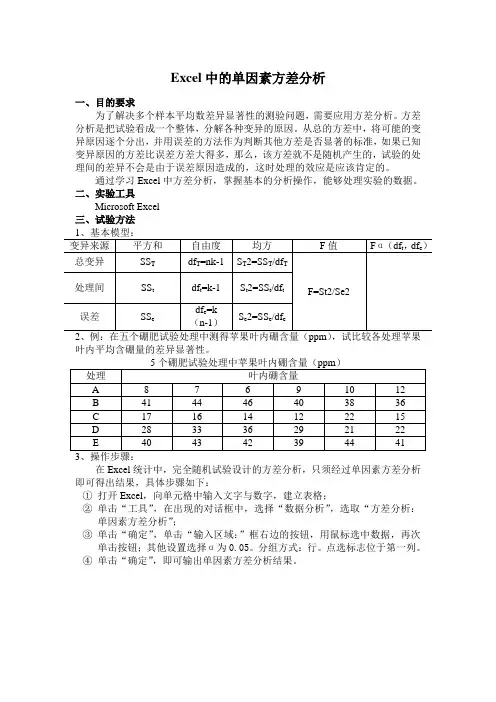
Excel中的单因素方差分析一、目的要求为了解决多个样本平均数差异显著性的测验问题，需要应用方差分析。
方差分析是把试验看成一个整体，分解各种变异的原因。
从总的方差中，将可能的变异原因逐个分出，并用误差的方法作为判断其他方差是否显著的标准，如果已知变异原因的方差比误差方差大得多，那么，该方差就不是随机产生的，试验的处理间的差异不会是由于误差原因造成的，这时处理的效应是应该肯定的。
通过学习Excel中方差分析，掌握基本的分析操作，能够处理实验的数据。
二、实验工具Microsoft Excel三、试验方法叶内平均含硼量的差异显著性。
在Excel统计中，完全随机试验设计的方差分析，只须经过单因素方差分析即可得出结果，具体步骤如下：①打开Excel，向单元格中输入文字与数字，建立表格；②单击“工具”，在出现的对话框中，选择“数据分析”，选取“方差分析：单因素方差分析”；③单击“确定”，单击“输入区域：”框右边的按钮，用鼠标选中数据，再次单击按钮；其他设置选择α为0.05。
分组方式：行。
点选标志位于第一列。
④单击“确定”，即可输出单因素方差分析结果。
4、方差分析输出结果：SUMMARY组观测数求和平均方差A 6 52 8.666667 4.666667B 6 245 40.83333 13.76667C 6 96 16 11.6D 6 169 28.16667 34.96667E 6 249 41.5 3.5差异源SS df MS F P-value F crit 组间5160.467 4 1290.117 94.1691 1.07E-14 2.75871 组内342.5 25 13.7总计5502.967 295、多重比较：由方差分析的结果，采用新复极差测验法，再稍加计算比较处理，即可得出：60.05显著，并可知除E与B二处理间无极显著差异外，其他均有极显著差异。
SPSS中的单因素方差分析一、基本原理单因素方差分析也即一维方差分析，是检验由单一因素影响的多组样本某因变量的均值是否有显著差异的问题，如各组之间有显著差异，说明这个因素（分类变量）对因变量是有显著影响的，因素的不同水平会影响到因变量的取值。
如何在Excel中灵活运用ttest函数Excel是一款广泛应用于数据分析和计算的电子表格软件。
其中，ttest函数是一种用于假设检验的函数，能够帮助用户判断两个样本的均值是否有显著差异。
在本文中，我们将介绍如何在Excel中灵活运用ttest函数进行数据分析。
一、ttest函数简介ttest函数是Excel中的一个统计函数，用于进行t检验，即根据样本数据判断两个总体均值是否存在显著差异。
该函数的语法为：TTEST(array1, array2, tails, type)，其中：- array1：表示第一个样本的数据范围；- array2：表示第二个样本的数据范围；- tails：表示假设检验的尾数，可以选择1或2。
当tails为1时，表示单尾检验；当tails为2时，表示双尾检验；- type：表示ttest函数的类型，可以选择1、2或3。
当type为1时，表示两个样本的方差相等；当type为2时，表示两个样本的方差不等且样本大小相等；当type为3时，表示两个样本的方差不等且样本大小不等。
二、ttest函数的应用下面以一个实例来说明如何在Excel中灵活运用ttest函数。
假设我们有两组数据，分别为X组和Y组，在Excel的两列中分别输入这两组数据。
然后，在Excel的任意一个单元格中输入以下公式：=TTEST(A1:A10, B1:B10, 2, 3)其中，A1:A10表示X组的数据范围，B1:B10表示Y组的数据范围，2表示双尾检验，3表示两个样本的方差不等且样本大小不等。
按下Enter键后，Excel会自动计算出ttest函数的结果，包括t值、自由度、双尾概率等信息。
根据这些信息，我们可以判断这两组数据的均值是否存在显著差异。
三、ttest函数的结果解读ttest函数的结果包括t值、自由度、双尾概率等信息。
其中，t值越大表示两个样本的均值差异越显著，自由度越大表示样本数据越多，双尾概率表示根据t值和自由度计算得出的两个样本均值差异的概率。
excel anova 函数【原创实用版】目录1.EXCEL ANOVA 函数的概述2.ANOVA 函数的适用场景3.ANOVA 函数的基本语法4.ANOVA 函数的实例解析5.ANOVA 函数的结论解读正文1.EXCEL ANOVA 函数的概述在 EXCEL 中，ANOVA 函数是一种用于分析数据方差的函数，其全称为“分析方差”，主要用于单因素方差分析。
它可以帮助我们判断不同样本均值之间是否存在显著性差异，从而为我们提供数据分析的依据。
2.ANOVA 函数的适用场景ANOVA 函数主要适用于以下场景：- 对比三个或以上样本均值的差异；- 分析各样本均值间是否存在显著性差异；- 评估样本数据是否符合正态分布。
3.ANOVA 函数的基本语法在 EXCEL 中，ANOVA 函数的基本语法如下：```=ANOVA(range1, range2, range3,...)```其中，range1、range2、range3 等表示需要进行方差分析的数据范围。
需要注意的是，数据范围需要用逗号分隔，且各数据范围的大小应相同。
4.ANOVA 函数的实例解析假设我们有一组数据，需要分析不同品牌饮料的口感评分是否存在显著性差异。
数据如下：```品牌 | 口感评分----|-------A | 85, 90, 88, 92B | 80, 82, 85, 88C | 87, 90, 89, 91```我们可以使用 ANOVA 函数进行分析，具体操作如下：```=ANOVA(C1:C4, D1:D4, E1:E4)```函数结果显示，p 值为 0.05，小于 0.05，说明各品牌饮料的口感评分存在显著性差异。
5.ANOVA 函数的结论解读根据 ANOVA 函数的结果，我们可以得出以下结论：- 如果 p 值小于 0.05，说明各样本均值之间存在显著性差异；- 如果 p 值大于等于 0.05，说明各样本均值之间不存在显著性差异。
如何在Excel中进行统计假设检验和推断分析在Excel中进行统计假设检验和推断分析是经济学、统计学和数据分析领域的基础技能之一。
统计假设检验常用于判断数据样本是否符合某种分布或是否有显著的差异，而推断分析则用于从样本数据中得出总体的特征。
本文将介绍如何在Excel中进行这两种分析，并给出具体示例和操作步骤。
第一章：统计假设检验1.1 单样本均值检验单样本均值检验用于判断样本均值是否与已知的总体均值有显著的差异。
在Excel中，可以使用T.TEST函数进行单样本均值检验。
具体操作步骤如下：（1）在输入数据所在列中输入样本数据；（2）选择一个空白单元格，输入=T.TEST(数据范围，已知均值)；（3）按下回车键，即可得到检验的结果。
1.2 配对样本均值检验配对样本均值检验用于判断配对样本的均值差异是否显著。
在Excel中，可以使用T.TEST函数和数据分析工具进行配对样本均值检验。
具体操作步骤如下：（1）在两个列中输入配对样本数据；（2）点击“数据”选项卡，在“分析”工具中选择“数据分析”；（3）从弹出窗口中选择“t-检验：配对两样本”的选项，点击“确定”；（4）在对话框中输入“输入范围”和“相关系数”；（5）点击“确定”，即可得到检验结果。
1.3 独立样本均值检验独立样本均值检验用于判断两个独立样本的均值是否有显著差异。
在Excel中，可以使用T.TEST函数和数据分析工具进行独立样本均值检验。
具体操作步骤如下：（1）在两个列中分别输入两个独立样本数据；（2）点击“数据”选项卡，在“分析”工具中选择“数据分析”；（3）从弹出窗口中选择“t-检验：两独立样本的方差不等”的选项，点击“确定”；（4）在对话框中输入“输入范围”和“类型”；第二章：推断分析2.1 单样本推断单样本推断用于从一个样本数据中得出总体的特征。
在Excel 中，可以使用T.INV函数进行单样本推断。
具体操作步骤如下：（1）在输入数据所在列中输入样本数据；（2）选择一个空白单元格，输入=T.INV(置信水平, 自由度)；（3）按下回车键，即可得到推断结果。
如何在Excel中使用ANOVA进行方差分析方差分析（ANOVA）是一种常用的统计分析方法，用于比较两个或多个样本之间的均值是否存在统计显著性差异。
在Excel中，我们可以利用内置的数据分析工具paketo进行ANOVA分析，具体步骤如下：1. 数据准备首先，我们需要将待分析的数据准备好。
假设我们要比较三种不同药物对某种疾病的治疗效果，我们可以将每种药物的治疗结果记录在Excel的不同列中，每个样本的观测值放在不同行中，确保数据排列整齐。
2. 打开数据分析工具paketo点击Excel工具栏上的“数据”选项卡，在“数据分析”组中找到“数据分析”按钮，点击打开数据分析对话框。
3. 选择ANOVA工具在数据分析对话框中，找到并选中“方差分析（ANOVA）”工具，然后点击“确定”按钮。
4. 填写输入范围在ANOVA工具的对话框中，需要填写“输入范围”和“Alpha”值。
“输入范围”即为待分析的数据范围，可以手动输入或通过点击选择数据表中的相关数据区域。
“Alpha”值用于设置显著性水平，默认为0.05，可以根据需要适当调整。
5. 设置输出选项在ANOVA工具的对话框中，可以对输出结果进行设置。
一般情况下，选择“新工作表里输出”即可，这样可以在新的工作表中查看分析结果。
6. 点击确定，进行分析完成以上设置后，点击“确定”按钮开始进行ANOVA分析。
7. 分析结果解读分析完成后，Excel将会在指定的输出位置生成ANOVA的结果。
通过观察各个因素的P值，我们可以判断各组间的均值是否存在显著差异。
从ANOVA结果中，我们可以查看总体方差（Between groups）和误差方差（Within groups），并计算出F值和P值。
若P值小于显著性水平，则可以认为各个样本之间的均值存在显著差异。
总结：通过Excel中的数据分析工具paketo，我们可以轻松地进行ANOVA方差分析。
只需将待分析数据准备好，选择合适的工具，填入相应的参数，即可得到分析结果。
excel假设检验方法Excel可以使用多种方法进行假设检验。
以下是一些常见的假设检验方法，并为每种方法提供了Excel中的函数示例：1. 单样本t检验：使用T.TEST函数。
例如，=T.TEST(range, sample_mean, tails)用于检验一个样本平均值与一个给定的总体平均值之间是否存在显著差异。
2. 双样本t检验：使用T.TEST函数。
例如，=T.TEST(range1, range2, tails, type)用于检验两个样本均值之间是否存在显著差异。
3. 配对样本t检验：使用T.TEST函数。
例如，=T.TEST(range1, range2, 2, 1)用于检验一组相关的配对观测值之间是否存在显著差异。
4. 方差分析（ANOVA）：使用ANOVA函数。
例如，=ANOVA(range1, range2, range3, ...)用于检验多个样本均值之间是否存在显著差异。
5. 卡方检验：使用CHISQ.TEST函数。
例如，=CHISQ.TEST(observed_range, expected_range)用于检验观测频数与期望频数之间是否存在显著差异。
6. 相关性检验：使用CORREL函数计算相关系数，然后使用T.TEST函数检验相关系数是否显著。
例如，=T.TEST(CORREL(range1, range2), sample_size-2, tails)用于检验两个变量之间的相关性是否显著。
这些是Excel中常用的假设检验方法和相应函数的示例。
根据具体的假设检验问题，你可以选择合适的方法并使用相应的函数进行分析。
