七年级下册第一章《认识三角形》单元检测(含答案)

2019年七年级下册数学单元测试题第一单元三角形的初步认识一、选择题1．在△ABC和△A′B′C′中，已知 AB=A′B′，∠B=∠B′，要保证△ABC ≌△A′B′C′，可补充的条件是（）A．∠B+∠A=90°B． AC=A′C′C．BC=B′C′D．∠A+∠A′=90°答案：C2．如图所示是跷跷板的示意图，支柱0C与地面垂直，点0是横板AB的中点，AB可以绕着点0上下转动，当A端落地时，∠0AC=20°．跷跷板上下可转动的最大角度（即∠A′OA）是（）A．800 B．60°C．40°D．20°答案：C3．△ABC中，∠A：∠B：∠C=1：2：3，则△ABC为（）A．锐角三角形B．直角三角形C．钝角三角形D．锐角或钝角三角形答案：B4．如图所示，在直角三角形ABC中，AC≠AB，AD是斜边BC上的高，DE⊥AC，DF⊥AB，垂足分别是E，F，则图中与∠C（除°C外）相等的角的个数是（）A．2个B．3个C．4个D．5个答案：B5．如图所示，把三角形纸片ABC沿DE折叠，当点A落在四边形BCDE内部时，则∠A 与∠l+∠2之间有一种数量关系始终保持不变，你认为该规律是（）A．∠A=∠l+∠2 B．2∠A=∠l+∠2C．3∠A=2∠1+∠2 D．3∠A=2（∠1+∠2）答案：B二、填空题6．在△ABC 和△DEF 中，AB=4，，∠A=35°，∠B =70°, DE=4 ,∠D = ，∠E=70°，根据判定△ABC≌△DEF.解析：35°, ASA7．在Rt△ABC中，∠C=90°，CE是△ABC的中线，若AC=2．4 cm，BC=1．5 cm，则△AE的面积为．解答题解析：0.9cm28．如图，△ABC是不等边三角形，DE=BC，以D ，E为两个顶点作位置不同的三角形，使所作的三角形与△ABC全等，这样的三角形最多可以画出_______个．解析：49．如图，已知ΔABC≌ΔADE，则图中与∠BAD相等的角是．解析：∠CAE10．已知ABC DEF20cm，那么△DEF中EF==，△ABC的面积是2BC EF△≌△，5cm边上的高是__________cm．解析：811．如图所示，∠1=∠2，∠ABC=∠DCB，AC，BD相交于O，请将下列说明AB=DC的理由的过程补充完整．解：∵∠ABC=∠DCB，∠l=∠2(已知)，∴∠ABC一∠l=∠DCB一∠2，即∠DBC= ．在△ABC和△DCB中，= ( )，= ( )，= ( )，∴≌ ( )，∴AB=DC( )．解析：∠ACB，∠ACB，∠DBC，已证，∠ABC，∠DCB，已知，BC，CB，公共边，△ABC，△DCB，AAS，全等三角形对应边相等12．如图所示，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃．最省事的办法是带去，理由是．解析：③，可根据③中的两角及夹边画出一个与之全等的三角形13．如图所示，已知点D，E，F分别是BC，AC，DC的中点，△EFC的面积为6 cm2，则△ABC的面积为．解析：48cm214．如图所示，△ABC中，D，E是BC边上的两点，且BD=DE=EC，则AD是三角形的中线，AE是三角形的中线．解析：ABE，ACD15．如图所示，∠1= ．解析：120°16．(1)自行车用脚架撑放比较稳定的原因是．(2)若AABC的三边长都为整数，周长为11，有一边长为4，且任何两边都不相等，则这个三角形的最大边长为．解析：(1)三角形的稳定性；(2)517．如图，已知AB=AC=8 cm ，BE ⊥AC 于E ，CD ⊥AB 于D ．若AD=5 cm ，则EC= cm ．解析：3三、解答题18． 如图，把4×4的正方形方格图形分割成两个全等图形，请在下图中，沿虚线画出四种不同的分法，把4×4的正方形分割成两个全等图形.解析：19．已知：△ABC 的周长为 18 cm ，AB 边比AC 边短2 cm ，BC 边是AC 边的一半，求△ABC 三边的长.解析：AB=6 cm ，BC=4cm ，AC=8cm20．看图按要求完成问题：(1）画ABC ∆边BC 的中线和B ∠的平分线；(2）分别指出直角三角形DE 和EF 边上的高线；(3）画钝角三角形OP 边上的高线．QP O F E D C B A （2） （1） （3）解析：略21．根据条件作图：(1)任意画一个Rt△ABC，使∠C=90°；(2)画∠CAB的平分线交对边于D；(3)画出点D到Rt△ABC的斜边的垂线段DE．解析：略22．如图所示，已知∠α，线段a，b，求作一个三角形，使其两边长分别为a，a+b，两边的夹角等于∠α．解析：略23．如图①所示，长方形通过剪切可以拼成直角三角形，方法如下：仿照上图，用图示的方法，解答下列问题：(1)如图②所示，已知直角三角形，设计一种方案，将它分成若干块，再拼成一个与之等面积的长方形；(2)如图③所示，对任意一个三角形，设计一种方案，把它分成若干块，再拼成一个与它等面积的长方形．解析：（1）(2）24．如图所示，已知AD=AE，∠l=∠2．请说明OB=OC成立的理由．解析：略25．如图所示，已知△ABE≌△ACE，D是BC的中点，你能说明△BDE≌△CDE吗?解析：略26．如图所示，已知△ABD≌△ACE，AD=6 cm，AC=4 cm，∠ABD=50°，∠E=30°．求BE的长和∠COD的度数．解析：BE=2 cm，∠COD=20°27．如图所示，已知△ABC≌△DCB，其中AB=DC，试说明∠ABD=∠ACD的理由．解析：略28．如图所示，AD是△ABC的一条中线也是BC边上的高，试说明：(1)△ABD≌△ACD；(2)∠B=∠C，AB=AC．请完成下面的说理过程．解：(1)∵AD是△ABC的高(已知)，∴∠BDA=∠CDA=90°( )．∵AD是△ABC的中线(已知)，∴BD=CD( )．当把图形沿AD对折时，射线DB与射线DC重合，∴点B与点重合．∴△ABD与△ACD ．∴△ABD≌△ACD( )．(2)∵△ABD≌△ACD(已知)，∴AB=AC，∠B=∠C( )．解析：(1)三角形高线的定义，三角形中线的定义，C，重合，全等三角形的定义；(2)全等三角形对应边、对应角分别相等29．在下列图形中，分别画出△ABC的三条高．解析：略30．在△ABC中，∠A+∠C=120°，∠B+∠C=110°，求三角形各内角的度数．解析：∠A=70°，∠B=60°，∠C=50°。

2019年七年级下册数学单元测试题第一单元 三角形的初步认识一、选择题1．如图，CD 是△ABC 的中线，DE 是△ACD 的中线，BF 是△ADE 的中线，若△AEF 的面积是 1cm 2，则△ABC 的面积是（ ）A ． 4cm 2B ．5 cm 2C ． 6 cm 2D ．8 cm 2答案：D2．如图，AD ，BE 都是△ABC 的高，则与∠CBE 一定相等的角是（ ）A ．∠ABEB ．∠BADC ．∠DACD ．以上都不是答案：C3．如图，直线123,,l l l 表示三条相互交叉的公路，现要建造一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（ ）A ．一处B ．两处C ．三处D ．四处答案：D4．如图所示，由∠ABC=∠DCB ，∠ACB=∠DBC ，直接能判定全等的三角形是 （ ）A ．△AB0≌△DODB ．△ABC ≌△DCB C ．△ABD ≌△DCA D ．△OAD ≌△0BC答案：B5．如图所示，在Rt △ABC 中，∠BAC=90°，AD 是高，则图中互余的角有（ ）A ． 2对B ．3对C ．4对D ．5对答案：C6．将矩形ABCD 沿AE 折叠．得到如图所示的图形，已知∠CED ′=60°．那么∠AED 的大小是（ ）A ．50°B ．55°C ．60°D ．75°答案：C7．以下列各组线段的长为边，能构成三角形的是（ ）A ．4 cm ，5 cm ，6 cmB ．2 cm ，3 cm ，5 cmC ．4 cm ，4 cm 。

9 cmD ．12 cm ，5 cm ，6 cm答案：A8．一个三角形的两边长分别是3和6，第三边长为奇数，那么第三边长是（ ）A 5或7B ．7或9C ．3或5D ．9答案：A二、填空题9．在△ABC 和△DEF 中，AB=4，，∠A=35°，∠B =70°, DE=4 ,∠D = ，∠E=70°，根据 判定△ABC ≌△DEF.解析：35°, ASA10．如图，AB ＝AC ，要使ACD ABE ∆∆≌，应添加的条件是____________ (添加一个条件即可)解析：B C ∠=∠（答案不唯一）11．在ABC △中，BC 边不动，点A 竖直向上运动，A ∠越来越小，BC ∠∠，越来越大．若A ∠减少α度，B ∠增加β度，C ∠增加γ度，则αβγ，，三者之间的等量关系是 ．解析：αβγ=+12．已知BD 是ΔABC 的一条中线, 如果ΔABD 和ΔBCD 的周长分别是21,12,则BC AB -的长是 ．解析：913．在下列条件中：①∠A+∠B=∠C ；②∠A ∶∠B ∶∠C=1∶2∶3；③∠A=900－∠B ；④∠A=∠B=12∠C 中，能确定△ABC 是直角三角形的条件有 个. 解析：414．如图所示：(1)若△ABD ≌△ACE ，AB=AC ，则对应边还有 ，对应角有 ．(2)若△BOE ≌△COD ，则0E 的对应边是 ，∠EB0的对应角是 ；(3)若△BEC ≌△CDB ，则相等的边有 ．解析： (3)BE=CD ，CE=BD ，BC=CB (1)AD 与AE ，BD 与CE ；∠A 与∠A ，∠ABD 与∠ACE ，∠ADB 与∠AEC ；(2)OD ，∠DCO ；15．如图所示，已知点D ，E ，F 分别是BC ，AC ，DC 的中点，△EFC 的面积为6 cm 2，则△ABC 的面积为 ．解析：48cm 216．已知△ABC 三边为a,b ，c ，且a ，b 满足21(3)0a b -+-=，c 为整数，则c 的取值为 ．解析：3三、解答题17．如图，DB 是△ABC 的高，AE 是∠BAC 的角平分线，∠BAE=26°，求∠BFE 的度数.解析：64°18．如图所示，已知∠α，线段a，b，求作一个三角形，使其两边长分别为a，a+b，两边的夹角等于∠α．解析：略19．如图所示，已知线段a，b和∠α，用直尺和圆规作△ABC，使∠B=∠α，AB=a，BC=b．解析：略20．如图所示，已知∠E=∠F=90°，∠B=∠C，AE=AF，则以下结论有哪些是成立的?并挑选一个将理由补充完整．①∠1=∠2；②BE=CF；③CD=FN；④△AEM≌△AFN．成立的有：．我选，理由如下：解析：①②④，以下略21．如图所示，已知AD=AE，∠l=∠2．请说明OB=OC成立的理由．解析：略22．如图所示，以Rt△ABC的两直角边AB，BC为边向外作正△ABE和正△BCF，连结EF，EC，请说明EF=EC．解析：略23．如图所示，四边形ABCD 中，AB=CD，BC=AD，请你添一条辅助线，把它分成两个全等的三角形．你有几种添法?分别说明理由．解析：连结AC或连结BD，都是根据SSS说明三角形全等24．请你在如图所示的方格纸中，画一个与左上角已有图形全等的图形．解析：略25．如图所示，把△ACB沿着AB翻转，点C与点D重合，请用符号表示图中所有的全等三角形．解析：△ACE≌△ADE，△BCE≌△BDE，△ACB≌△ADB26．如图所示为由6个面积为1的小正方形组成的矩形，点A，B，C，D，E，F，G是小正方形的顶点，以这7个点中的任意三个点为顶点，可组成多少个面积为1的三角形?请写出所有满足条件的三角形．解析：共l4个三角形，具体表示略27．A，B是平面上的两个固定点，它们之间的距离为5 cm，请你在平面上找一点C(1)要使点C到A，B两点的距离之和等于5 cm ，则C点在什么位置?(2)要使点C到A，B两点的距离之和大于5 cm ，则点C在什么位置?(3)能使点C到A，B两点的距离之和小于5 cm吗?为什么?解析：(1)点C在线段AB上；(2)点C在线段AB外；(3)不能，因为两点之间线段最短(为5 cm)28．如图所示，已知△ABC．画出AC边上的中线BM和∠BAC的平分线AD．解析：略29．已知△ABC中，以点A为顶点的外角为120°，∠B=30°，求∠C的度数．解析：∠C=90°30．如图所示，在Rt △ABC中，∠ACB为直角，∠CAD的平分线交BC的延长线于点E，若∠B=35°，求∠BAE和∠E的度数．解析：∠E=27．5°，∠BAF=117．5°。

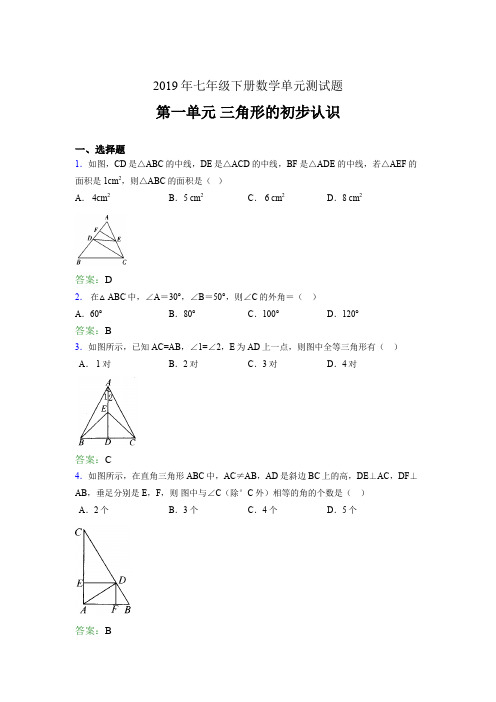
2019年七年级下册数学单元测试题第一单元三角形的初步认识一、选择题1．如图，CD是△ABC的中线，DE是△ACD的中线，BF 是△ADE 的中线，若△AEF 的面积是 1cm2，则△ABC的面积是（）A． 4cm2B．5 cm2C． 6 cm2D．8 cm2答案：D2．在△ABC中，∠A＝30°，∠B＝50°，则∠C的外角＝（）A．60°B．80°C．100°D．120°答案：B3．如图所示，已知AC=AB，∠1=∠2，E为AD上一点，则图中全等三角形有（）A． 1对B．2对C．3对D．4对答案：C4．如图所示，在直角三角形ABC中，AC≠AB，AD是斜边BC上的高，DE⊥AC，DF⊥AB，垂足分别是E，F，则图中与∠C（除°C外）相等的角的个数是（）A．2个B．3个C．4个D．5个答案：B5．如果三角形的两边长分别为7和2，且它的周长为偶数，那么，第三边的长为（） A．5 B．6 C．7 D．8答案：C6．以下列各组线段的长为边，能构成三角形的是（）A．4 cm，5 cm，6 cm B．2 cm，3 cm，5 cmC．4 cm，4 cm。

9 cm D．12 cm，5 cm，6 cm答案：A7．在△ABC和△A′B′C′中，①AB=A′B′；②BC=B′C′；③AC=A′C′；④∠A=∠A′；⑤∠B=∠8′；⑥∠C=∠C′，则下列条件中不能使△ABC≌△A′B′C′的是（）A．②④⑤B．①②③C．①③⑤D．①②⑤答案：C8．下列说法中：①如果两个三角形可以依据“AAS”来判定全等，那么一定也可以依据“ASA”来判定它们全等；②如果两个三角形都和第三个三角形不全等，那么这两个三角形也一定不全等；③要判断两个三角形全等，给出的条件中至少要有一对边对应相等．正确的是（）A．①和②B．②和③C．①和③D．①②③答案：C二、填空题9．如果一个三角形的两个角都是80°，那么第三个角的度数是 .解析：20°10．如图，在△ABC中，∠ACB=90°，角平分线 AD、BE交于点F，则∠AFB= .解析：135°11．如图，∠A=80°，∠2=130°,则∠l= ．解析：130°12．要使△ABC≌△A′B′C′，已知AB=A′B′，∠B=∠B′，如果利用“ASA”，要补充条件，如果利用“AAS”，要补充条件．解析：∠A=∠A′，∠=∠C′13．如图所示，已知∠C=∠B，AC=AB，请写出一个与点D有关的正确结论：．解析：AD=AE等14．如图所示，已知AB=DC，要说明△ABC≌△DCB，还需增加一个条件：．解析：∠ABC=∠DCB或AC=BD15．如图所示，△ABC中，DE是AC的中垂线，AE=5，△ABC的周长为30，则△ABD 的周长是．解析：2016．已知△ABC≌△A′B′C′，AB+AC=18 cm，BC=7 cm，则△A′B′C′的周长是．解析：25 cm17．如图所示，△ABC中，D，E是BC边上的两点，且BD=DE=EC，则AD是三角形的中线，AE是三角形的中线．解析：ABE，ACD18．已知△ABC三边为a,b，c，且a，b满足2-+-=，c 为整数，则c的取值1(3)0a b为．解析：319．如图所示，共有 个三角形．其中以DC 为一边的三角形是 ．解析：7；△DBC ，△ADC三、解答题20．如图，已知 AB=DC ，AD=BC ，说出下列判断成立的理由：(1)△ABC ≌△ACD ； (2)∠B=∠D.解析：略21．如图，AD ，CE 分别是△ABC 的两条高，问∠BAD 与∠BCE 相等吗？请说明理由．解析：相等，理由略22．如图，AD 平分∠BAC ，AB ＝AC ，则BD ＝CD ，试说明理由．A BCD E解析：△ABD≌△ACD（SAS），则BD=CD．23．根据条件作图：(1)任意画一个Rt△ABC，使∠C=90°；(2)画∠CAB的平分线交对边于D；(3)画出点D到Rt△ABC的斜边的垂线段DE．解析：略24．如图所示，已知线段a，b，c，用直尺和圆规作△ABC，使AB=c，BC=a，AC=b．解析：略25．如图所示，△ABC≌△ADE，试说明BE=CD的理由．解析：略26．如图所示，△ABC与△DFE全等，AC与DE是对应边．(1)找出图中相等的线段和相等的角；(2)若BE=14 cm，FC=4 cm，求出EC的长．解析：(1)BF=CE，AC=DE，AB=DF，BC=EF，∠A=∠D，∠B=∠EFD，∠ACB=∠E；(2)5 cm27．三角形的三条中线、三条高、三条角平分线都分别交于一点，其中交点可能不在三角形内部的是哪种线段?请通过画图说明．解析：高线的交点可以在三角形的外部、内部及其顶点上28．如图所示为由6个面积为1的小正方形组成的矩形，点A，B，C，D，E，F，G是小正方形的顶点，以这7个点中的任意三个点为顶点，可组成多少个面积为1的三角形?请写出所有满足条件的三角形．解析：共l4个三角形，具体表示略29．一个三角形有两条边相等，它的最长的边比最短的边多2，已知这个三角形的周长为8，求它的三条边长．解析：103，103，4330．如图所示，在△ABC中，∠B=35°，∠C=75°，AD是△ABC的角平分线．(1)∠BAC等于多少度?(2)∠ADC等于多少度?解析：(1)70°；(2)70°。

2019年七年级下册数学单元测试题第一单元三角形的初步认识一、选择题1．如图，CD是△ABC的中线，DE是△ACD的中线，BF 是△ADE 的中线，若△AEF 的面积是 1cm2，则△ABC的面积是（）A． 4cm2B．5 cm2C． 6 cm2D．8 cm2答案：D2．已知在△ABC 和△A′B′C′中，AB =A′B′，∠B=∠B′，补充下面一个条件，不能说明△ABC≌△A′B′C′的是（）A． BC =B′C′B．AC=A′C′C．∠C=∠C′D．∠A=∠A′答案：B3．AD是△ABC中BC边上的中线，若AB＝4，AC＝6，则AD的取值范围是（）A．AD＞1 B．AD＜5 C．1＜AD＜5 D．2＜AD＜10答案：C4．如图，△ABC≌△DCB，AB=5cm，AC=7 cm，BC=8 cm，那么DC的长是（）A．8 cm B．7 cm C．6cm D．5 cm答案：D5．如图所示，0P平分∠AOB，PE⊥OB，PF⊥OA，则下列结论中正确的个数有（）①OE=0F；②FP=PE；③OP⊥EF；④∠PEF=∠PFE；⑤0P平分∠FPE；⑥PQ=0QA．6个B．5个C．4个D．2个答案：B6．如图，△ABD≌△CDB，∠ABD=40°，∠C=110°，则∠CBD等于（）A．20°B．30°C．40°D．50°AB PO答案：B7．关于三角形的高的位置，下列判断中正确的是（ ）A ．必在三角形内B ．必在三角形外C ．不在三角形内，就在三角形外D ．以上都不对答案：D8．三角形的三边长都是整数，并且唯一的最长边是5，则这样的三角形共有（ ）A 1个B ．2个C ．3个D ．4个答案：D二、填空题9．如图，点P 在AOB ∠的平分线上，若使AOP BOP △≌△，则需添加的一个条件是 ．（只写一个即可，不添加辅助线）解析：OA ＝OB10．若一个三角形的三个内角这比为2：3：4，则三个内角中最小的内角为 ． 解析：40°11．如图：请写出图中有 个三角形，分别是 ．解析：3，ΔABD、ΔAB C 、ΔA CD 12．已知△ABC 中，AB=AC ，①当它的两个边长分别为8 cm 和3 cm 时，它的周长为 cm ；②如果它的周长为18 cm ，一边的长为4 cm ，则腰长为 cm.解析：19cm ，7cm13．如图所示，已知AC 和BD 相交于0，A0=C0，∠A=∠C ，说出BO=D0的理由．解：∵AC 和BD 相交于0，∴∠AOB= ( )． 在△AOB 和△COD 中，∠AOB= (已证)，= (已知)，∴△AOB≌△COD( )．∴BO=D0( )．解答题解析：∠COD，对顶角相等，∠COD，A0，C0，∠A，∠C，ASA，全等三角形的对应边相等14．如图所示，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃．最省事的办法是带去，理由是．解析：③，可根据③中的两角及夹边画出一个与之全等的三角形15．如图所示，分别根据下列已知条件，再补充一个条件，使图中的△ABD≌△ACE(SAS)．①AB=AC，∠A=∠A，；②AB=AC，∠B=∠C, ；③AD=AE，，BD=CE．解析：①AD=AE；②BD=CE；③∠ADB=∠AEC16．如图所示，四边形ABCD为正方形，它被虚线分成了9个小正方形，则△DBE与△DEC的面积之比为．解析：1：217．已知△ABC三边为a,b，c，且a，b满足2a b-+-=，c 为整数，则c的取值1(3)0为．解析：318．如图所示．(1)图中共有 个三角形，分别是 ；(2)∠CDB 是 的内角，是 的外角；(3)在AACD 中，∠A 是边 和 的夹角，边AC 是 的对边．解析：(1)3；△ACD ，△BCD ，△ABC ；(2)△BDC ，△ACD ；(3)AD ，AC ，∠ADC19．四条长度分别是2，3，4，5的线段，任选3条可以组成 个三角形． 解析：3三、解答题20．如图，AB ⊥BD 于B ，DE ⊥BD 于D ，已知AB ＝CD ，BC ＝ED,求∠ACE 的度数．解析：△ABC ≌△CDE （SAS ），则∠ACB=∠E ，由于∠ACB+∠ACE =∠E+∠D, 则∠ACE=∠D=90°．21．如图所示，有1l ，2l ，3l 三条公路交于A ，B ，C ，现要在△ABC 内建一加油站，使它到三 条公路的距离相等，问应如何建?作出加油站的位置，并说明理由．解析：分别作∠ABC 与∠BCA 的角平分线，两条角平分线的交点即为加油站的位置，根据角平分线上的点到角两边的距离相等即可说明22．如图所示，已知线段a，c，求作Rt△ABC，使BC=a，AB=c．解析：提示：两种情况23．如图所示，已知AD=AE，∠l=∠2．请说明OB=OC成立的理由．解析：略24．如图所示，△ABC≌△ADE，试说明BE=CD的理由．解析：略25．如图所示，已知△ABC≌△DCB，其中AB=DC，试说明∠ABD=∠ACD的理由．解析：略26．如图所示，在△ABC中，∠ABC=∠ACB，且∠ACB=2∠A，BD⊥AC于D，求∠DBC的度数．解析：18°27．如图所示，在△ABC中，∠A=∠ACB，CD是∠ACB的平分线，CE⊥AB于E．(1)试说明∠CDB=3∠DCB；(2)若∠DCE=48°，求∠ACB的度数．解析：(1)略；(2)28°28．如图所示，已知△ABC的边AB和BC边上的中线AD，请把△ABC补画完整．解析：连结BD，并延长BD到C，使DC=BD，连结AC29．已知△ABC中，以点A为顶点的外角为120°，∠B=30°，求∠C的度数．解析：∠C=90°30．如图所示，在Rt △ABC中，∠ACB为直角，∠CAD的平分线交BC的延长线于点E，若∠B=35°，求∠BAE和∠E的度数．解析：∠E=27．5°，∠BAF=117．5°。

2019年七年级下册数学单元测试题第一单元 三角形的初步认识一、选择题1．下列说法错误的是（ ）A ．有一个外角是锐角的三角形是钝角三角形B ．有两个角互余的三角形是直角三角形C ．直角三角形只有一条高D ．任何一个三角形中，最大角不小于60度答案：C2．一块试验田的形状是三角形（设其为ABC △），管理员从BC 边上的一点D 出发，沿DC CA AB BD →→→的方向走了一圈回到D 处，则管理员从出发到回到原处在途中身体（ ）A ．转过90B ．转过180C ．转过270D ．转过360答案：D3．如图，123，，∠∠∠的大小关系为（ ）A ．213>>∠∠∠B ．132>>∠∠∠C ．321>>∠∠∠D ．123>>∠∠∠ 答案：D4．如图所示，BA=BD ，BC=BE ，根据“边角边”条件得到△ABE △DBC ，则需要增加条件 （ ）A ．∠A=∠DB ．∠E=∠C C ．∠A=∠CD ．∠l=∠2答案：D5．任意一个三角形被一条中线分成两个三角形，则这两个三角形：①形状相同，②面积相同，③全等．上述说法正确的有（ ）A ．0个B ．1个C ．2个D ．3个答案：B6．△ABC 中，∠A ：∠B ：∠C=1：2：3，则△ABC 为（ ）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．锐角或钝角三角形答案：B7．如图所示，在直角三角形ABC 中，AC ≠AB ，AD 是斜边BC 上的高，DE ⊥AC ，DF ⊥AB ，垂足分别是E ，F ，则 图中与∠C （除°C 外）相等的角的个数是（ ）A ．2个B ．3个C ．4个D ．5个答案：B8．下列叙述中正确的个数是（ ）①三角形的中线、角平分线都是射线；②三角形的中线、角平分线都在三角形内部；③三角形的中线就是过一边中点的线段；④三角形三条角平分线交于一点．A ．0个B ．1个C ．2个D ．3个答案：C9．现有两根木棒，它们的长度分别是20 cm 和30 cm ．如果不改变木棒的长度，要钉成一个三角形木架，那么应在下列四根木棒中选取（ ）A ．10 cm 的木棒B ．20 cm 的木棒C ．50 cm 的木棒D ．60 cm 的木捧 答案：B二、填空题10．如图，在△ABC 和△CDA 中，((______(________)AB DC BC DA =⎧⎪=⎨⎪=⎩已知）已知）, 所以△ABC ≌△CDA( ).解析：AC ，CA ，公共边，SSS11．如图，，已知OA=OB ，OC=OD ，D 和BC 相交于点E ，则图中全等三角形有 对.解析：412．一个三角形中最多有个内角是钝角，最多可有个角是锐角.解析：1,313．如图，在△ABC中，AB=AC=10cm，DE是AB的中垂线，△BDC 的周长为 16 cm，则 BC 的长为 .解析：6cm14．如图，长方形ABCD中(AD＞AB)，M为CD上一点，若沿着AM折叠，点N恰落在BC上，∠ANB＋∠MNC＝____________．解析：90°15．如图，△ABC是不等边三角形，DE=BC，以D ，E为两个顶点作位置不同的三角形，使所作的三角形与△ABC全等，这样的三角形最多可以画出_______个．解析：416．如图所示，已知点C是∠AOB角平分线上的一点，点P，P′分别在边0A，OB上，如果要得到OP=OP′，需添加以下条件中的某一个即可，请你写出所有可能结果的序号：．①∠0CP=∠OCP′；②∠0PC=∠OP′C；③PC=P′C；④PP′⊥0C；⑤PC⊥OA，P′C ⊥OB．解析：①②④⑤17．如图所示，△ABC中，DE是AC的中垂线，AE=5，△ABC的周长为30，则△ABD 的周长是．解析：2018．如图所示，在△ABC中，AD是角平分线，已知∠B=66°，∠C=38°，那么∠ADB= ，∠ADC= ．解析：76°，l04°19．已知△ABC三边为a,b，c，且a，b满足2-+-=，c 为整数，则c的取值a b1(3)0为．解析：3三、解答题20．如图，已知BE=CF，AB=CD，∠B=∠C，则AF=DE吗?请说明理由．解析：利用SAS说明△ABF≌△DCE21．如图所示，已知线段a，b，c，用直尺和圆规作△ABC，使AB=c，BC=a，AC=b．解析：略22．画一个三角形，使两个内角分别为45°和60°，它们的夹边为2．5cm．解析：略23．如图所示，以Rt△ABC的两直角边AB，BC为边向外作正△ABE和正△BCF，连结EF，EC，请说明EF=EC．解析：略24．如图所示，已知AB=AE，∠B=∠E，BC=ED，F是CD的中点，说出AF是CD的中垂线的理由．解：连结AC，AD，在△ABC和△AED中，AB=AE(已知)，∠B=∠E(已知)，BC=ED(已知)，∴△ABC≌△AED(SAS)．∴AC=AD(全等三角形的对应边相等)．请把后面的过程补充完整：解析：略25．请你在如图所示的方格纸中，画一个与左上角已有图形全等的图形．解析：略26．如图所示，把△ACB沿着AB翻转，点C与点D重合，请用符号表示图中所有的全等三角形．解析：△ACE≌△ADE，△BCE≌△BDE，△ACB≌△ADB27．如图所示，在四边形ABCD中，E，F分别为AD，BC的中点．已知四边形ABCD的面积为l，求四边形DEBF的面积．解析：1228．如图所示，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=34°，求∠DAE的大小．解析：18°29．已知，如图所示，△ABC中，∠B=30°，∠C=40°，D为BC上一点，∠1=∠2，求∠BAD的度数．解析：∠l=∠2=70°，∠1=∠B+∠BAD，得∠BAD=40°30．在△ABC中，已知∠A+∠B=70°，∠C=2∠A，求∠A，∠B，∠C的度数．解析：∠A=55°，∠B=15°，∠C=110°。

2019年七年级下册数学单元测试题第一单元 三角形的初步认识一、选择题1．在△ABC 和△A ′B ′C ′中，已知 AB=A ′B ′，∠B=∠B ′，要保证△ABC ≌△A ′B ′C ′，可补充的条件是（ ）A ．∠B+∠A=90°B ． AC=A ′C ′ C ．BC=B ′C ′D ．∠A+∠A ′=90° 答案：C2．．如图，已知△ABC 的六个元素，则下面甲、乙、丙三个三角形中和△ABC 全等的图形是（ ）A ．甲和乙B ．乙和丙C ．只有乙D ．只有丙 答案：C3．用直尺和圆规作一个角等于已知角的示意图如下，则说明∠A′O′B′＝∠AOB 的依据是（ ）A ．SSSB ．SASC ．ASAD ．AAS答案：A4．如图，123，，∠∠∠的大小关系为（ ）A ．213>>∠∠∠B ．132>>∠∠∠C ．321>>∠∠∠D ．123>>∠∠∠ 答案：D5．在△ABC 中，∠A 是锐角，那么△ABC 是（ ）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不能确定 答案：D6． 如图，O 是直线AB 上的一点，过O 点作射线OC ，已知OD 、OE 分别平分∠AOC 、∠COB ．则△ODE 是（ ）A ．钝角三角形B ．锐角三角形C ．直角三角形D ．无法判断 答案：C7．如图所示，已知∠1=∠2，AD=CB ，AC ，BD 相交于点0，MN 经过点O ，则图中全等三角形的对数为（ ）A ．4对B ．5对C ．6对D ．7对答案：C8．如图所示，已知AD⊥BC，BD=CD，则①△ABD≌△ACD，②△ABD和△ACD不全等，③AB=AC，④∠BAD=∠CAD，以上判断正确的是（）A．①B．②C．①③④D．①②③答案：C9．如图所示，已知△ABC≌△DCB，那么下列结论中正确的是（）A．∠ABC=∠CDB，∠BAC=∠DCB，∠ACB=∠DBCB．∠ABC=∠DCB，∠BAC=∠CDB，∠ACB=∠ABDC．∠ABC=∠DCB，∠BAC=∠CDB，∠ACB=∠DBCD．∠ABC=∠DBC，∠BAC=∠CDB，∠ACB=∠ACD答案：C10．如图所示，△ABD≌△CDB，∠ABD=40°，∠CBD=30°，则∠C等于（）A．20°B．100°C．110°D．115°答案：C11．如图所示，在4×4的正方形网格中，∠l，∠2，∠3的大小关系是（）A．∠l>∠2>∠3 B．∠1=∠2>∠3C．∠l<∠2=∠3 D．∠l=∠2=∠3答案：B二、填空题12．如图，A，B，C，D，E，F是平面上的6个点，则∠A+∠B+∠C+∠D+∠E+∠F的度数是．解析：360°13．仔细观察下图：(1)图中的△ABC与△A′B′C′全等吗? ．(2)由图中的信息，你可以得到的重要结论是：．解析：(1)不全等；(2)有两边及其中一边的对角对应相等的两个三角形不一定全等14．△ABC与△DEF全等，AB=DE，若∠A=50°，∠B=60°，则∠D= ．解析：50°或60°15．如图所示，四边形ABCD为正方形，它被虚线分成了9个小正方形，则△DBE与△DEC的面积之比为．解析：1：216．如图所示，∠1=135°，∠2=75°，则∠3的度数是．解析：30°17．已知△ABC三边为a,b，c，且a，b满足2-+-=，c 为整数，则c的取值1(3)0a b为．解析：318．(1)自行车用脚架撑放比较稳定的原因是．(2)若AABC的三边长都为整数，周长为11，有一边长为4，且任何两边都不相等，则这个三角形的最大边长为．解析：(1)三角形的稳定性；(2)5三、解答题19．如图，在△ABC中，AD垂直平分 BC，H是AD上的一点，连接BH、CH.(1)AD平分∠BAC吗？为什么？(2)你能找出几对相等的角？请把它们写出来(不需写理由).解析：( 1)由△ADB≌△ADC(SAS)，得∠BAD=∠CAD. (2)7对，∠BHD = ∠CHD，∠ABD = ∠ACD，∠HBD =∠HCD, ∠BDA=∠CDA,∠ABH=∠ACH,∠AHB=∠AHC，∠BAD=∠CAD20．如图，直线OA，OB表示两条相互交叉的公路．点M，N表示两个蔬菜基地．现要建立一个蔬菜批发市场，要求它到两个基地的距离相等，并且到公路OA，OB的距离解析：分别作AOB的平分线OC和线段MN的垂直平分线DE，则射线OC与直线DE的交点P即为批发市场应建的地方．21．如图所示，已知线段a，b，c，用直尺和圆规作△ABC，使AB=c，BC=a，AC=b．解析：略22．画一个三角形，使两个内角分别为45°和60°，它们的夹边为2．5cm．解析：略23．如图所示，A，D，F，B在同一直线上，AD=BF，AE=BC，且∠A=∠B，说明下列各式成立的理由．(1)△AEF≌△BCD；(2)∠BFE=∠ADC．解析：略24．如图所示，已知AB=AE，∠B=∠E，BC=ED，F是CD的中点，说出AF是CD的中垂线的理由．解：连结AC，AD，在△ABC和△AED中，AB=AE(已知)，∠B=∠E(已知)，BC=ED(已知)，∴△ABC≌△AED(SAS)．∴AC=AD(全等三角形的对应边相等)．请把后面的过程补充完整：解析：略25．如图所示为由6个面积为1的小正方形组成的矩形，点A，B，C，D，E，F，G是小正方形的顶点，以这7个点中的任意三个点为顶点，可组成多少个面积为1的三角形?请写出所有满足条件的三角形．解析：共l4个三角形，具体表示略26．如图所示，画出△ABC的角平分线BD，AB边上的高CE，BC边上的中线AF．解析：略27．如图所示，在△ABC中，∠A=∠ACB，CD是∠ACB的平分线，CE⊥AB于E．(1)试说明∠CDB=3∠DCB；(2)若∠DCE=48°，求∠ACB的度数．解析：(1)略；(2)28°28．如图所示，已知△ABC．画出AC边上的中线BM和∠BAC的平分线AD．解析：略29．(1)为了求出四边形的内角和，你能根据图中的两种添线方法，分别求出四边形的内角和吗?(2)请你用类似的方法求出五边形、六边形的内角和，比较一下，你发现了什么规律?(3)利用你发现的规律，可以求得20边形的内角和为度．解析：(1)360°；(2)规律：n边形的内角和为(n-2)·180°；(3)324030．如图，O是线段AC，BD的交点，并且AC=BD，AB=CD，小刚认为图中的两个三角形全等，他的思考过程是：在△AB0和△DC0中，AC=BD，∠AOB=∠DOC，AB=CD =>△AB0≌△DC0．你认为小刚的思考过程正确吗?如果正确，指出他用的是哪种三角形全等识别法；如果不正确，请你增加一个条件，并说明你的思考过程．解析：不正确，增加一个∠A=∠D(或∠B=∠C)的条件即可通过“AAS”证明，或增加一个A0=0D(或BO=OC)的条件即可通过“SAS”证明三角形全等．。

2019年七年级下册数学单元测试题第一单元 三角形的初步认识一、选择题1．如图，从下列四个条件：①BC=B ′C ，②AC=A ′C ，③∠A ′CA =∠B ′CB ，④AB=A ′B ′中，任取三个为条件，余下的一个为结论，则最多可以构成正确结论的个数是（ ）A ． 1B ．2C ．3D ．4答案：B2．在△ABC 和△A ′B ′C ′中，已知 AB=A ′B ′，∠B=∠B ′，要保证△ABC ≌△A ′B ′C ′，可补充的条件是（ ）A ．∠B+∠A=90°B ． AC=A ′C ′ C ．BC=B ′C ′D ．∠A+∠A ′=90° 答案：C3．在ABC △中，275A B ∠=∠=，则C ∠=（ ）A ．30°B ．135°C ．105°D ．67°30′答案：D4． 用一副三角板画图，不能画出的角的度数是（ ）A ．15°B ．75°C ．145°D ．165°答案：C5．如图所示，已知CD=CE ，AE=BD ，∠ADC=∠BEC=100°，∠ACD=26°，则∠BCD 的度数是 （ ）A ．72°B ．54°C ． 46°D ．20°答案：C6．如图所示，△ABC ≌△BAD ．A 与B ，C 与D 是对应顶点，若AB=4cm ，BD=4．5cm，AD=1．5 cm，则BC的长为（）A 4．5 cm B．4 cm C．1．5 cm D．不能确定答案：C7．如果三角形的一个外角是锐角，那么这个三角形是（）A．锐角三角形B．钝角三角形C．直角三角形D．以上三种都可能答案：B8．如图，AB=CD，∠l=∠2，AO=3，则AC=（）A．3 B．6 C．9 D．12答案：B二、填空题9．如图，∠B=∠DEF，AB=DE，要证明△ABC ≌△DEF,(1)若以“ASA”为依据，需添加的条件是；(2)若以“SAS”为依据，需添加的条件是 .解析：∠A = ∠D，BC=EF(或BE=CF)10．如图，在△ABC中，∠ACB=90°，角平分线 AD、BE交于点F，则∠AFB= .解析：135°11．如图，在△ABC中，AB=AC=10cm，DE是AB的中垂线，△BDC 的周长为 16 cm，则 BC 的长为 .解析：6cm12．若a、b、c为△ABC的三边，则a b ca b c---+0(填“>”、“=”或“<”) .解析：<13．要使△ABC≌△A′B′C′，已知AB=A′B′，∠B=∠B′，如果利用“ASA”，要补充条件，如果利用“AAS”，要补充条件．解析：∠A=∠A′，∠=∠C′14．如图所示，已知AB=DC，要说明△ABC≌△DCB，还需增加一个条件：．解析：∠ABC=∠DCB或AC=BD15．只要三角形三边的长度固定，这个三角形的和就完全确定，三角形的这个性质叫做三角形的．解析：形状，大小，稳定性16．如图，若把△ABC绕A点旋转一定角度就得到△ADE，那么对应边AB= ，AC= ，BC= ；对应角∠CAB= ，∠B= ，∠C= ．解析：AD，AE，DE，∠EAD，∠D，∠E17．如图所示，△ABC三条中线AD、BE、CF交于点0，S△ABC=l2，则S△ABD= ，S△AOF= ．解析：6，218．如图所示，四边形ABCD为正方形，它被虚线分成了9个小正方形，则△DBE与△DEC的面积之比为．解析：1：219．如图所示，AD是△ABC的中线，AB=8．AC=6,则△ABD与△ACD的周长之差是．解析：220．如图所示，∠1=135°，∠2=75°，则∠3的度数是．解析：30°21．四条长度分别是2，3，4，5的线段，任选3条可以组成个三角形．解析：322．等腰三角形两边长分别是7cm和3 cm，则第三边长是．解析：7 cm三、解答题23．如图，在△ABC中，∠B=44°，∠C=72°，AD是△ABC的角平分线．(1)求∠BAC的度数；(2)求∠ADC的度数．D CB A解析：∠BAC=64°，∠ADC=108°．24．如图所示，已知∠β=30°，a=3 cm ．用直尺和圆规完成下列尺规作图(不写作法，保留 痕迹)，求作△ABC ，使∠B=∠β，BC=a ，AC=1．5 cm ．解析：略25．如图所示，已知线段a ，b ，c ，用直尺和圆规作△ABC ，使AB=c ，BC=a ，AC=b ．解析：略26．如图所示，四边形ABCD 中，AB=CD ，BC=AD ，请你添一条辅助线，把它分成两个全等的三角形．你有几种添法?分别说明理由．解析：连结AC或连结BD，都是根据SSS说明三角形全等27．如图所示，试沿着虚线，把图形划分成两个全等图形．解析：略28．如图所示，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=34°，求∠DAE的大小．解析：18°29．如图所示，已知△ABC．画出AC边上的中线BM和∠BAC的平分线AD．解析：略30．在△ABC中，∠A+∠C=120°，∠B+∠C=110°，求三角形各内角的度数．解析：∠A=70°，∠B=60°，∠C=50°。

2019年七年级下册数学单元测试题第一单元三角形的初步认识一、选择题1．下列说法错误的是（）A．有一个外角是锐角的三角形是钝角三角形B．有两个角互余的三角形是直角三角形C．直角三角形只有一条高D．任何一个三角形中，最大角不小于60度答案：C2．如图，将两根钢条AA′、BB′的中点O连在一起，使AA′、BB′可以绕着点O自由转动，就做成了一个测量工件，则A′B′的长等于内槽宽AB，那么判定△OAB≌△OA′B′的理由是（）A．边角边B．角边角C．边边边D．角角边答案：A3．．如图，已知△ABC的六个元素，则下面甲、乙、丙三个三角形中和△ABC全等的图形是（）A．甲和乙B．乙和丙C．只有乙D．只有丙答案：C4．如图所示，已知∠1=∠2，AD=CB，AC，BD相交于点0，MN经过点O，则图中全等三角形的对数为（）A．4对B．5对C．6对D．7对答案：C5．任意一个三角形被一条中线分成两个三角形，则这两个三角形：①形状相同，②面积相同，③全等．上述说法正确的有（）A．0个B．1个C．2个D．3个答案：B6．△ABC中，∠A：∠B：∠C=1：2：3，则△ABC为（）A．锐角三角形B．直角三角形C ．钝角三角形D ．锐角或钝角三角形答案：B7．如图所示，在Rt △ABC 中，∠BAC=90°，AD 是高，则图中互余的角有（ ）A ． 2对B ．3对C ．4对D ．5对答案：C8．如图所示，AD ⊥BC 于D ，那么以AD 为高的三角形有（ ）A ． 3个B ．4个C ． 5个D ．6个答案：D9．三角形一边上的中线把原三角形分成两个（ ）A ．形状相同的三角形B ．面积相等的三角形C ．直角三角形D ．周长相等的三角形答案：B二、填空题10．如果一个三角形的三条高都在三角形的内部，那么这个三角形是 三角形(按角分类). 解析：锐角11．全等三角形的对应边 ，对应角 ．解析：相等，相等12． 已知三角形的两边长分别为3cm 和7cm ，第三边的长为偶数，则这个三角形的周长为 .解析：16cm 或18cm13．在下列条件中：①∠A+∠B=∠C ；②∠A ∶∠B ∶∠C=1∶2∶3；③∠A=900－∠B ；④∠A=∠B=12∠C 中，能确定△ABC 是直角三角形的条件有 个. 解析：414．如图所示：(1)若△ABD ≌△ACE ，AB=AC ，则对应边还有 ，对应角有 ．(2)若△BOE≌△COD，则0E的对应边是，∠EB0的对应角是；(3)若△BEC≌△CDB，则相等的边有．解析： (3)BE=CD，CE=BD，BC=CB (1)AD与AE，BD与CE；∠A与∠A，∠ABD与∠ACE，∠ADB与∠AEC；(2)OD，∠DCO；15．已知△ABC三边为a,b，c，且a，b满足21(3)0-+-=，c 为整数，则c的取值a b为．解析：316．如图所示．(1)图中共有个三角形，分别是；(2)∠CDB是的内角，是的外角；(3)在AACD中，∠A是边和的夹角，边AC是的对边．解析：(1)3；△ACD，△BCD，△ABC；(2)△BDC，△ACD；(3)AD，AC，∠ADC 17．已知三角形的两条边的长分别是3和5，第三条边的长为a，则a的长度在和之间．解析：2，8三、解答题18．如图，，已知 AD平分∠CAB，且DC⊥AC，DB⊥AB，那么AB和AC相等吗？请说明理由.解析：AB =AC，理由略19．2008年 10月 18 日上午 10时，经过中国铁建十六局集团和中铁隧道局集团2000多名员工4年零2个月的顽强拼搏，被誉为世界级工程难题的宜万铁路野三关隧道Ⅱ线胜利贯通. 如图，这是工程建设中一个山峰的平面图，施工队在施工之前需要先测量出隧道AB的长度，请你利用三角形全等的知识设计一种测量方法，并说明理由.解析：利用全等三角形的判定(AAS，SAS，ASA)来设计完成20．如图所示，在△ABC中，a=2．7cm，b=1．7 cm，c=1．9 cm，∠B=38°，∠C=44°．请你从中选择适当的数据，画出与△ABC全等的三角形．(把你能画的三角形全部画出来，不写画法，但要在所画的三角形中标出用到的数据)解析：利用全等判别方法去画，图略21．画一个三角形，使两个内角分别为45°和60°，它们的夹边为2．5cm．解析：略22．如图①所示，长方形通过剪切可以拼成直角三角形，方法如下：仿照上图，用图示的方法，解答下列问题：(1)如图②所示，已知直角三角形，设计一种方案，将它分成若干块，再拼成一个与之等面积的长方形；(2)如图③所示，对任意一个三角形，设计一种方案，把它分成若干块，再拼成一个与它等面积的长方形．解析：（1）(2）23．如图所示，以Rt△ABC的两直角边AB，BC为边向外作正△ABE和正△BCF，连结EF，EC，请说明EF=EC．解析：略24．如图所示，已知点A，B，C，D在一条直线上，AB=CD．AE=DF，EC=FB，说明∠ACE=∠DBF的理由．解析：略25．三月三，放风筝，如图所示是小明制作的风筝，他根据DE=DF，EH=FH，不用度量，就知道∠DEH=∠DFH．请你运用所学知识给予说明．解析：提示：连结DH26．如图所示，△ABC≌△ADE，试说明BE=CD的理由．解析：略27．如图所示，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=34°，求∠DAE的大小．解析：18°28．已知三角形的周长是46 cm，其中一边比最短边长2 cm，比最长边短3 cm,求三角形三边的长．解析：13 cm，15 cm，18 cm29．如图所示，在△ABC中，∠B=35°，∠C=75°，AD是△ABC的角平分线．(1)∠BAC等于多少度?(2)∠ADC等于多少度?解析：(1)70°；(2)70°30．如图，O是线段AC，BD的交点，并且AC=BD，AB=CD，小刚认为图中的两个三角形全等，他的思考过程是：在△AB0和△DC0中，AC=BD，∠AOB=∠DOC，AB=CD =>△AB0≌△DC0．你认为小刚的思考过程正确吗?如果正确，指出他用的是哪种三角形全等识别法；如果不正确，请你增加一个条件，并说明你的思考过程．解析：不正确，增加一个∠A=∠D(或∠B=∠C)的条件即可通过“AAS”证明，或增加一个A0=0D(或BO=OC)的条件即可通过“SAS”证明三角形全等．。

2019年七年级下册数学单元测试题第一单元 三角形的初步认识一、选择题1．在△ABC 中，三个内角满足以下关系：∠A=12∠B=13∠C ，那么这个三角形是（ ） A ．直角三角形 B ．锐角三角形 C ．钝角三角形 D ．任意三角形 答案：A2．下列各条件中，不能作出惟一三角形的是（ ）A ．已知两边和夹角B ．已知两角和夹边C ．已知两边和其中一边的对角D ．已知三边答案：C3．如图，123，，∠∠∠的大小关系为（ ） A ．213>>∠∠∠ B ．132>>∠∠∠ C ．321>>∠∠∠ D ．123>>∠∠∠ 答案：D4．任何一个三角形的三个内角中至少有（ ）A ．一个角大于60°B ．两个锐角C ．一个钝角D ．一个直角 答案：B5．如图所示，已知AD=CB ，∠AD0=∠CB0，那么可用“SAS”全等识别法说明的是（ ）A ．△AD0≌△CB0B ．△AOB ≌△CODC ．△ABC ≌△CDAD ．△ADB ≌△CBD答案：D6．如图所示，已知△ABC ≌△DCB ，那么下列结论中正确的是（ ）A ．∠ABC=∠CDB ，∠BAC=∠DCB ，∠ACB=∠DBCB ．∠ABC=∠DCB ，∠BAC=∠CDB ，∠ACB=∠ABDC ．∠ABC=∠DCB ，∠BAC=∠CDB ，∠ACB=∠DBCD ．∠ABC=∠DBC ，∠BAC=∠CDB ，∠ACB=∠ACD7．如图，△ABD≌△DCA，B和C是对应顶点，则∠ADB和∠DAC所对的边是（）A．A0和DO B．AB和DC C．A0和BD D．D0和AC答案：B8．如图所示，AD⊥BC于D，那么以AD为高的三角形有（）A． 3个B．4个C． 5个D．6个答案：D9．如果三角形的两边长分别为7和2，且它的周长为偶数，那么，第三边的长为（）A．5 B．6 C．7 D．8答案：C10．如果三条线段的比是：（1）1：4：6；（2）1：2：3；（3）3：4：5；（4）7：7：11；（5）3 ： 3：6，那么其中可构成三角形的比有（）A．1种B．2种C．3种D．4种答案：B11．下列长度的三条线段，能组成三角形的是（）A．6，3，3 B．4，8，8 C．3，4，8 D．8，l5，7答案：B12．在△ABC和△A′B′C′中，①AB=A′B′；②BC=B′C′；③AC=A′C′；④∠A=∠A′；⑤∠B=∠8′；⑥∠C=∠C′，则下列条件中不能使△ABC≌△A′B′C′的是（）A．②④⑤B．①②③C．①③⑤D．①②⑤答案：C二、填空题13．在Rt△ABC中，∠C=90°，CE是△ABC的中线，若AC=2．4 cm，BC=1．5 cm，则△AE的面积为．解答题14．如图所示，△ABC中，DE是AC的中垂线，AE=5，△ABC的周长为30，则△ABD 的周长是．解析：2015．如图所示，分别根据下列已知条件，再补充一个条件，使图中的△ABD≌△ACE(SAS)．①AB=AC，∠A=∠A，；②AB=AC，∠B=∠C, ；③AD=AE，，BD=CE．解析：①AD=AE；②BD=CE；③∠ADB=∠AEC16．如图所示，已知△ABD≌△ACE，∠B=∠C，那么AB= ，AD= ， BD= ，∠A= ，∠ADB= ．解析：AC，AE，CE，∠A，∠AEC17．如图所示，四边形ABCD为正方形，它被虚线分成了9个小正方形，则△DBE与△DEC的面积之比为．解析：1：218．如图所示，△ABC中，D，E是BC边上的两点，且BD=DE=EC，则AD是三角形的中线，AE是三角形的中线．解析：ABE ，ACD19．如图所示，∠1= ．解析：120°20．如果三角形的三个内角都相等，那么这个三角形是 三角形．解析：等边21．如图，在△ABC 中，已知AD=ED ，AB=EB ，∠A=75°，那么∠1+∠C 的度数是 ．解析：75°三、解答题22．在△ABC 中，∠ACB=90°，AC=BC ，直线MN 经过点C ，且AD ⊥MN 于D ，BE ⊥MN 于E ．(1）当直线MN 绕点C 旋转到图1的位置时，有①△ADC ≌△CEB ；②DE=AD ＋BE ，请说明理由．(2）当直线MN 绕点C 旋转到图2的位置时， DE=AD －BE ，请说明理由；(3）当直线MN 绕点C 旋转到图3的位置时，试问DE ，AD ，BE 具有怎样的等量关系？请写出这个等量关系，不必说明理由．C B A ED 图1 N M A B C DE MN 图2 A C B E D N M 图3解析：（1）略；（2）略；（3）DE=BE －AD ．23．如图，AC ＝AE ，∠BAM ＝∠BND ＝∠EAC ， 图中是否存在与△ABE 全等的三角形?并说明理由．解析：存在△ABE ≌△ADC ，理由略24．根据条件作图：(1)任意画一个Rt △ABC ，使∠C=90°；(2)画∠CAB 的平分线交对边于D ；(3)画出点D 到Rt △ABC 的斜边的垂线段DE ．解析：略25．画一个三角形，使两个内角分别为45°和60°，它们的夹边为2．5cm ．解析：略26．如图所示，△ABC 中，AB=AC ，BE ，CD 分别是AC ，AB 的中线，说明下列各式成立的理由．(1)BE=CD ；(2)∠1=∠2． A D M C B EN解析：略27．三月三，放风筝，如图所示是小明制作的风筝，他根据DE=DF，EH=FH，不用度量，就知道∠DEH=∠DFH．请你运用所学知识给予说明．解析：提示：连结DH28．如图所示为由6个面积为1的小正方形组成的矩形，点A，B，C，D，E，F，G是小正方形的顶点，以这7个点中的任意三个点为顶点，可组成多少个面积为1的三角形?请写出所有满足条件的三角形．解析：共l4个三角形，具体表示略29．如图所示，在Rt△ABC中，∠A=∠B，CD是∠ACB的平分线，请判定CD与AB的位置关系，并说明理由．解析：CD⊥AB，理由略30．如图，已知∠A=∠D，AB=DE．AF=DC，图中有哪几对全等三角形?并选取其中一对说明理由．解析：△ABF≌△DEC，△FCB≌△CFE，△ABC≌△DEF，证明略。