193梯形同步测试题2

梯形同步练习题知识技能天地 一、填空题： 1、以线段16,13ab ==为梯形的两底，以10c =为一腰，则来一腰d 的长度取值范围是 .2、等腰梯形上底的长与腰长相等，一条对角线与一腰垂直，则梯形上底角 的度数等于 .3、梯形的上底长为6㎝，过上度的一顶点引一腰的平行线，交下底所构成的三角形周长为21㎝，那么该梯形的周长是 .4、已知直角梯形的两腰之比为1∶2，那么该梯形的最大角为 ，最小角为 .5、梯形ABCD 中，AD ∥BC ，AB=DC=2㎝ ，BD 平分∠ABC ，∠C=60°，则梯形的周长等于 ㎝.6、已知等腰梯形的两条对角线互相垂直，高为8㎝，则此等腰梯形两底的和是 .7、等腰梯形ABCD 中，AD ∥BC ，AD=AB ，BC=BD ，则∠A= .8、等腰梯形ABCD 中，AB ∥CD ，AC 平分∠DAB ，∠DAB=60° ，若梯形周长为8㎝，则AD = . 9.如图1, 梯形ABCD 中，AD//BC ，AB=CD=AD=1，∠B=60°，直线MN 为梯形ABCD 的对称轴，P 为MN 上一点，那么PC+PD 的最小值 ．图1 图210.如图2，是一块待开发的土地，规划人员把它分割成①号区，②号区，③号区三块，拟在①号区种花，②号区建房，③号区种树，已知图中四边形ABCD 与四边形EFGH 是两个相同的直角梯形，则①号区种花的面积是 ．11.如图3，是用形状、大小完全相同的等腰梯形镶嵌的图案，则这个图案中的等腰三角形的底角（指锐角）的度数是_____.12.直角梯形两底之差等于高，则其最大角等于_______.13.如图4，四边形ABCD 是等腰梯形，AD//BC ，AB=CD ，则AC=_______， ∠BAD=_____，∠BCD=_____，等腰梯形这个性质用文字语言可表述为_______．A BC D14.等腰梯形ABCD 中，对角线AC 、BD 相交于点O ，那么图中的全等三角形最多有________对.15.在四边形ABCD 中AD ∥BC ，但AD≠BC ，若使它成为等腰梯形，则需添加的条件是_____（填一个正确的条件即可）16.如图5,梯形ABCD 中,AB//CD,∠ABC=90°,AB=9cm,BC=8cm,CD=7cm,M 是AD 的中点,过M 作AD 的垂线交BC 于N,则BN 等于_____cm.图5 图617.如图6，梯形ABCD 中，AD ∥BC ，若∠B=60°，AC ⊥AB ，那么∠DAC= ． 18.如图7，在等腰梯形ABCD 中AD//BC ，AB=DC ，CD=BC ，E 是BA 、CD 延长线的交点， ∠E=40°，则∠ACD=____________度.图7 图819.如图8,在等腰梯形ABCD 中,AD//BC,AC 、BD 相交于点O ，有如下结论：①∠DAC=∠DCA ；②梯形ABCD 是轴对称图形； ③△AOB ≌△AOD ； ④AC=BD.请把其中正确结论的序号填写在横线上__________. 二、选择题：20、下列命题正确的有（ ）A 、等腰梯形两底角相等B 、底角相等的梯形是等腰梯形C 、等腰梯形对角线相等D 、对角线相等的四边形不是等腰梯形 21、如图9，梯形ABCD 中，AD ∥BC ，AC 、BD 相交于O ，则图中面积相等的三角形的对数有（ ） A 、4对 B 、1对 C 、2对 D 、3对22、在梯形ABCD 中，AB ∥CD ，AB >CD ，如果∠D >∠C ，那么AD 和BC 的关系是（ ）A 、AD >BCB 、AD=BC C 、AD <BC D 、不能确定 23、下列结论正确的是（ ）①梯形是轴对称图形，②等腰梯形是轴对称图形，③等腰梯形的对角线相等，④等腰梯形在同一底上的两个角相等A 、① ② ③B 、② ③ ④C 、① ③ ④D 、③ ④24、如果等腰梯形两底之差的一半等于它的高，那么此梯形的一个底角是（ ）A 、30°B 、45°C 、60°D 、75°图25、直角梯形一腰长为a ，这腰与一底所夹角为53倍直角，则另一腰长为（ ） A 、a B 、2a C 、12a D 、32a26. 若等腰三角形的三边长分别为3、4、11，则等腰三角形的周长为 （ ）.(Ａ)21 (Ｂ)29 (C)21或29 (Ｄ)21或22或2927. 如图10，在梯形ABCD 中，AD ∥BC ，AD=2，BC=8，AC=6，BD=8，则此梯形的面积是（ ）.（A ）24 （B ）20 （C ）16 （D ）12图10 图11 28. 如图11，等腰梯形ABCD 中，AD ∥BC ，AD=5，AB=6，BC=8，且AB ∥DE ，△DEC 的周长是（ ）.(A)3 (B)12 (C)15(D)1929. 等腰梯形上、下底差等于一腰的长，那么腰长与下底的夹角是（ ）.(A)75° (B)60° (C)45° (D)30°30．等腰梯形的高是腰长的一半,则底角为 （ ）.(A)30° (B)45° (C)60° (D)90°31．下列命题中，真命题是 （ ）.（A ）有一组对边平行，另一组对边相等的梯形是等腰梯形 （B ）有一组对角互补的梯形是等腰梯形 （C ）有一组邻角相等的四边形是等腰梯形 （D ）有两组邻角分别相等的四边形是等腰梯形32．如图12,在等腰梯形ABCD 中,AD=6cm,BD=9cm,AB=8cm,E 、F 、G 、H 分别是AD 、BD 、BC 、AC 的中点，那么四边形EFGH 的周长是 （ ）. (A)14cm (B)15cm (C)16cm(D)17cm图12 图13 图1433．如图13,等腰梯形ABCD,周长为40,∠BAD=60°,BD 平分∠ABC,则CD 的长为（ ）. (A)4 (B)5 (C)8 (D)1034．下列四边形中，两条对角线一定不相等．．．的是 （ ）. （A ）正方形 （B ）矩形 （C ）等腰梯形 （D ）直角梯形 35．如图14,等腰梯形ABCD 中，AB ∥DC ，AD=BC=8，AB=10，CD=6，则梯形ABCD 的面积是（ ）.（A ）1516 （B ）516 （C ）1532 （D ）171636.在下列图形中，沿着虚线将长方形剪成两部分，那么由这两部分既能拼成平行四边形，又能拼成三角形和梯形的是 （ ）.三、解答题：37、如图15，梯形ABCD 中，AD ∥BC ，BD ⊥CD ，AD=2，∠A=120°，AB=AD.求BC 的长.38、已知梯形ABCD 中，AB ∥CD ，AB >CD ，M 、N 分别是CD 、AB 的中点，且MN ⊥AB.求证：梯形ABCD 是等腰梯形.39、如图16，已知等腰梯形ABCD 中，AD ∥BC ，AD=3，AB=4，BC=7，求∠B40、如图17，在等腰梯形ABCD 中，AB ∥CD ，AB >CD ，AD=BC ，BD 平分∠ABC ，∠A=60°，梯形周长是20㎝，求梯形各边的长.探究创新乐园41、如图18，四边形ABCD 是等腰梯形，AD ∥BC ，AC ⊥BD ，AD+BC=10，求梯形的面积.42、要剪切如图19（尺寸单位：㎜）所示甲、乙两种直角梯形零件，且使两种零件的数量相等，有两种面积相等的矩形铝板可供选用.第一种长500㎜，宽300㎜；第二种长600㎜，宽250㎜.为了充分利用材料，应选第种铝板，这时一块铝板最多能剪甲、乙零件共个.剪下这些零件后，剩余的边角料的面积是㎜2.43、如图20，在四边形ABCD中，AD∥BC，∠B=30°，∠C=60°，点E、F、M、N分别是AB、CD、BC、DA 的中点，已知BC=7，MN=3，求EF的长.44.(12分)如图22,等腰梯形的上下底分别是3cm和5cm,一个角是45°,求等腰梯形的面积.图2245.(12分) 如图23，等腰梯形ABCD中，AB//CD，DC=AD=BC，且对角线AC垂直于腰BC，求梯形的各个内角.图2346.(14分) 如图24，梯形ABCD中，AB//CD，AD=BC，延长AB到E，使BE=DC，连结AC、CE.求证AC=CE.图2447.(14分)如图25，等腰梯形ABCD中，AD//BC，AD=3，AB=4，BC=7，求∠B的度数．4．图2548.(16分) 如图26,等腰梯形ABCD中，AD∥B，AB＝CD，DE⊥BC于E，AE＝BE，BF⊥AE于F，线段BF与图中的哪一条线段相等.先写出你的猜想，再加以证明图2649.(17分)如图27，在等腰梯形ABCD中，AB∥CD，AC、BD是对角线，将△ABD沿AB向下翻折到△ABE的位置，试判定四边形AEBC的形状，并证明你的结论．图27四、拓广探索(本题19分)如图28，四边形ABCD中，点E在边CD上，连结AE、BE.给出下列五个关系式：①AD∥BC；②DE=CE；③∠1=∠2；④∠3=∠4；⑤AD＋BC=AB．将其中的三个关系式作为题设，另外两个作为结论，构成一个命题．⑴用序号写出一个真命题（书写形式如：如果×××，那么××）；并给出证明；⑵用序号再写出三个真命题（不要求证明）；图28。

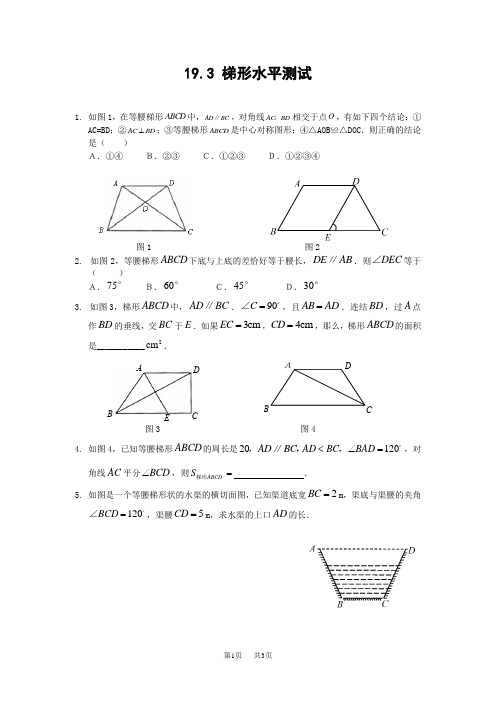
ＡDCBA DE CB19.3 梯形水平测试1. 如图1，在等腰梯形中，，对角线相交于点，有如下四个结论：①AC=BD；②；③等腰梯形是中心对称图形；④△AOB≌△DOC．则正确的结论是（）Ａ．①④Ｂ．②③Ｃ．①②③Ｄ．①②③④图1 图22. 如图2，等腰梯形下底与上底的差恰好等于腰长，．则等于（）Ａ．Ｂ．Ｃ．Ｄ．3. 如图3，梯形中，．，且．连结，过点作的垂线，交于．如果，，那么，梯形的面积是___________．图3 图44. 如图4，已知等腰梯形的周长是，对角线平分，则．5. 如图是一个等腰梯形状的水渠的横切面图，已知渠道底宽m，渠底与渠腰的夹角，渠腰m，求水渠的上口的长．ABCD AD BC∥AC BD，OAC BD⊥ABCDABCD DE AB∥DEC∠75°60°45°30°ABCD AD BC∥90C=∠AB AD=BD A BD BC E3cmEC=4cmCD=ABCD2cmABCD20AD BC，，∥120AD BC BAD<∠=，AC BCD∠ABCDS梯形=2BC=120BCD=∠5CD=AD6. 如图所示，已知在直角梯形ABCD中，∠B＝∠C＝90°，E为BC上的点，且EA＝ED，∠AEB＝75°，∠DEC＝45°，试说明AB＝BC．参考答案1、A2、B3、264、AD的长为9m5、理由略。

小学数学冀教版四年级下册梯形（四年级）同步测试姓名:_____________年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题（每空xx 分，共xx分）【题文】将方格图中的梯形划分成3个三角形，使它们面积的比是1：2：3．【答案】S△1：S△3：S△2=1：2：3【解析】做两条辅助线，即将梯形分为了三个三角形1、2、3；依据高相等，底的比即为面积比的特点，则这三个三角形即为要求画的三角形。

【题文】用下面给出的长度，画一个5cm2的梯形。

【答案】【解析】先依据三角形和梯形的面积确定出三角形的底为3厘米，高是2厘米；梯形的下底是3厘米，上底是2厘米，高是2厘米，于是可画出符合要求的图形。

评卷人得分【题文】以如图的这条线段为梯形的上底，作一个下底为4厘米、高为2.5厘米的梯形，并在图中标出下底和高的长度。

【答案】则梯形ABFE就是要求的下底为4厘米、高为2.5厘米的梯形。

【解析】经过已知的线段AB的顶点A，先画出它的一条垂线段AD，使AD=2.5厘米，再经过点D作线段AB 的平行线，根据梯形的定义和下底的长度，在平行线上截取一段EF=4厘米，由此即可画出这个梯形。

【题文】画一个直角梯形，其中上底长3厘米，下底长6厘米，高4厘米。

【答案】【解析】先画线段AB（3厘米）作为梯形的上底，由A点向下引垂线段AD（4厘米），画出梯形的高，接着画AB的平行线段DC（6厘米）作为梯形的下底，连接BC即可。

【题文】画出下面图形的高。

（2）利用如图的这个角画一个直角梯形。

【答案】【解析】在平行四边形中，从一条边上的任意一点向对边作垂线，这点与垂足间的距离叫做以这条边为底的平行四边形的高，平行四边形有无数条高，习惯上作平行四边形的高时都从一个顶点出发作一边的垂线，用三角板的直角可以画出平行四形的高；梯形两底间的距离就是梯形的高，通常过梯形上底的一个顶点用三角板的直角边向下底作垂线，这条垂线就是梯形的一条高；（2）用三角板过点A作AB的垂线，与过点C画AB的平行线相交于D，梯形ABCD就是所画的直角梯形。

AB E19.3梯形训练题基础训练一、选择题1、在下列命题中，正确的是（ ）A 、平行四边形的两条对角线相等B 、矩形的两条对角线互相垂直C 、菱形的两条对角线互相平分D 、等腰梯形的两条对角线互相平分2、如图，等腰梯形的两条对角线相交于O ，则图中全等的三角形有（ ）A 、4对B 、3对C 、2对D 、1对3、已知等腰梯形的底角为450，高等于上底，如果等腰梯形的下底为9，那么梯形的上底为（ ） A 、3 B 、5 C 、23 D 、324、在梯形ABCD 中，下底AB=14㎝，上底CD=6㎝，且∠A=300，∠B=600，则BC 的长为（ ） A 、8㎝ B 、6㎝ C 、4㎝ D 、3㎝ 二、填空题5、如果梯形的一组对角分别为1050和600，那么另外两个内角分别为 。

6、如果等腰梯形的两条对角线互相垂直，且梯形的高为4㎝，那么等腰梯形的面积为 。

7、已知梯形ABCD 的周长为40㎝，上底CD=6㎝，DE ∥BC 交AB 于E ，则△ADE 的周长为 。

8、在梯形ABCD 中，AD ∥BC ，∠B=900，AD=2，AB=6，BC=10，则CD 的长为 。

9、如图所示，在等腰梯形ABCD 中，AB ∥CD ，AC 平分∠DAB ，∠DAB=60°，若梯形的周长为10cm ，则AB= 。

三、解答题10、如图，在等腰梯形ABCD 中，CD ∥AB ，AB=9㎝， CD=4㎝，AD=5㎝，求∠B 的度数。

11、已知：如图，在梯形ABCD 中，AD ∥BC ，对角线AC ⊥BD ， AC=12㎝，BD=5㎝，求该梯形的面积。

12、如图所示，在梯形ABCD 中，AB ∥CD ，AD=BC ， 延长AB 到E ，使BE=DC ，连接AC ，CE ，求证：AC=CEAF A B 综合训练一、选择题1、如图，在梯形ABCD 中，AD ∥BC ，E 是CD 的中点，若△ABE 的面积为S ，则梯形ABCD 的面积为（ ）A 、2SB 、S 25 C 、S 47D 、S 492、如图，在梯形ABCD 中，AB ∥CD ，∠ABC=900，AB=9㎝，BC=8㎝，CD=7㎝，E 是AD 的中点，且EF ⊥AD 交BC 于F ，则BF 的长为（ ） A 、1㎝ B 、1.5㎝ C 、2㎝ D 、2.5㎝二、填空题3、如图，在梯形ABCD 中，AD ∥BC ，∠B+∠C=900，AD=5，BC=13，∠C=600，则该梯形的面积是 。

测试11 梯形(二)学习要求熟练运用所学的知识解决梯形问题．课堂学习检测一、回答下列问题1．梯形问题通常是通过分割和拼接转化为三角形或平行四边形，其分割拼接的方法有如下几种(如图)：(1)平移一腰，即从梯形的一个顶点______，把梯形分成一个平行四边形和一个三角形(图1所示)；图1 图2 图3 图4(2)从同一底的两端______，把梯形分成一个矩形和两个直角三角形(图2所示)；(3)平移对角线，即过底的一端______，可以借助新得的平行四边形或三角形来研究梯形(图3所示)；(4)延长梯形的两腰______，得到两个三角形，如果梯形是等腰梯形，则得到两个等腰三角形(图4所示)；(5)以梯形一腰的中点为______，作某图形的中心对称图形(图5、图6所示)；图5 图6 图7(6)以梯形一腰为______，作梯形的轴对称图形(图7所示)．二、填空题2．等腰梯形ABCD中，AD∥BC，若AD＝3，AB＝4，BC＝7，则∠B＝______3．如图，直角梯形ABCD 中，AB ∥CD ，CB ⊥AB ，△ABD 是等边三角形，若AB ＝2，则BC ＝______．4．在梯形ABCD 中，AD ∥BC ，AD ＝5，BC ＝7，若E 为DC 的中点，射线AE 交BC 的延长线于F 点，则BF ＝______． 三、选择题5．梯形ABCD 中，AD ∥BC ，若对角线AC ⊥BD ，且AC ＝5cm ，BD ＝12cm ，则梯形的面积等于( )． (A)30cm 2(B)60cm 2(C)90cm 2(D)169cm 26．如图，等腰梯形ABCD 中，AB ∥CD ，对角线AC 平分∠BAD ，∠B ＝60°，CD ＝2，则梯形ABCD 的面积是( )． (A)33 (B)6(C)36(D)127．等腰梯形ABCD 中，AB ∥CD ，AD ＝BC ＝8，AB ＝10，CD ＝6，则梯形ABCD 的面积是( )． (A)516 (B)1516(C)1716(D)1532综合、运用、诊断一、解答题8．已知：如图，等腰梯形ABCD 中，AD ∥BC ，对角线AC ＝BC ＋AD ．求∠DBC 的度数．9．已知，等腰梯形ABCD中，AD∥BC，∠ABC＝60°，AC⊥BD，AB＝4cm，求梯形ABCD 的周长．10．如图，在梯形ABCD中，AD∥BC，∠B＝90°，∠C＝45°，AD＝1，BC＝4，E为AB中点，EF∥DC交BC于点F，求EF的长．11．如图，在梯形ABCD中，AD∥BC，AB⊥AC，∠B＝45°，AD＝2，BC＝42，求DC 的长．拓展、探究、思考一、解答题12．如图，梯形纸片ABCD 中，AD ∥BC 且AB ≠DC ．设AD ＝a ，BC ＝b ．过AD 中点和BC中点的直线可将梯形纸片ABCD 分成面积相等的两部分．请你再设计一种方法：只需用剪子一次就可将梯形纸片ABCD 分割成面积相等的两部分，画出设计的图形并简要说明你的分割方法．13．(1)探究新知：如图，已知△ABC 与△ABD 的面积相等，试判断AB 与CD 的位置关系，并说明理由．(2)结论应用：①如图，点M ，N 在反比例函数)0(>=k xky 的图象上，过点M 作ME ⊥y 轴，过点N 作NF ⊥x 轴，垂足分别为E ，F ．试证明：MN ∥EF ．②若①中的其他条件不变，只改变点M，N的位置，如图所示．请判断MN与EF是否平行．参考答案1．(1)作一腰的平行线； (2)作另一底边的垂线； (3)作对角线的平行线； (4)交于一点； (5)对称中心； (6)对称轴． 2．60°． 3．3； 4．12． 5．A ． 6．A ． 7．B ．8．60°．提示：过D 点作DE ∥AC ，交BC 延长线于E 点．9．.348+ 10．.22311．.10 12．方法1：取)(21b a BM +=．连接AM ，AM 将梯形ABCD 分成面积相等的两部分．方法2：(1)取DC 的中点G ，过G 作EF ∥AB ，交BC 于点F ，交AD 的延长线于点E ． (2)连接AF ，BE 相交于点O ．(3)过O 任作直线MN 与AD ，BC 相交于点M ，N ，沿MN 剪一刀即把梯形ABCD 分成面积相等的两部分．13．(1)证明：分别过点C ，D 作CG ⊥AB ，DH ⊥AB ．垂足为G ，H ，如图1，则∠CGA ＝∠DHB ＝90°．图1∴CG ∥DH∵△ABC 与△ABD 的面积相等 ∴CG ＝DH∴四边形CGHD 为平行四边形 ∴AB ∥CD .(2)①证明：连结MF ，如图2，NE 设点M 的坐标为(x 1，y 1)，点N 的坐标为(x 2，y 2)， ∵点M ，N 在反比例函数)0(>=k xky 的图象上，图2∴x 1y 1＝k ，x 2y 2＝k ． ∵ME ⊥y 轴，NF ⊥x 轴， ∴OE ＝y 1，OF ＝x 2．∴S △EFM ＝21x 1y 1＝21k ． ∴S △EFN ＝21x 2y 2＝21k ．∴S △EFM ＝S △EEN ．由(1)中的结论可知：MN ∥EF ． ②如图3所示，MN ∥EF ．图3。

19.3梯形
梯形问题中经常用到的辅助线
1．下列说法中正确的是(
) A ． 等腰梯形两底角相等 B ． 等腰梯形的一组对边相等且平行
C ． 等腰梯形同一底上的两个角都等于90°
D ． 等腰梯形的四个内角中不可能有直角
2．已知等腰梯形的周长25cm ，上、下底分别为7cm 、8cm ，则腰长为_____cm ．
3．等腰梯形中一个锐角为70°，则另外三个角分别为____， ____， ____．
4.5. 已知：如图，在等腰梯形ABCD 高DF =2，求腰DC 如果将本题改为 (1)已知下底、腰、高，求上底；
(2)已知上底、下底、腰，求高．你能解决这个问题吗？
说出你的思路．
B
C A B C
D F
6已知：如图，四边形ABCD 是等腰梯形，AD =BC ，AD =5，CD =2，AB =8，求梯形ABCD 的面积．
7.已知：如图，等腰梯形ABCD ，AD ∥BC ，对角线AC ⊥BD ，AD =3cm ，BC =7cm ． 求梯形的面积．
8. 如图，梯形ABCD 中，AD ∥BC ，∠A =90°，
∠D =150°，CD =8cm ，则AB = ．
D A B C
F A B
D A B D C。

梯形
一、按要求做题。

①②③
1.仔细观察，上面三个图形的相同特征是：。

2. 画出上面三个梯形的高，并标出上底和下底。

二、慧眼识珠。

1. 梯形有（）条高。

A.1
B.3
C.无数
2. 一个梯形中最多有（）个直角。

A.1
B.2
C.3
3. 梯形的内角和是（）。

A.180°
B.360°
C.540°
三、判断。

(1)梯形的一组对边相等。

( )
(2)梯形的高是两腰之间的垂直线段。

( )
(3)两腰相等的梯形叫做等腰梯形。

( )
(4)梯形只有一条高。

( )
四、实际运用。

1．一个等腰梯形的周长是25 cm，两腰的长度都是6 cm，上底是5 cm，下底的长度是多少厘米?
2．下面是一张长方形纸对折两次后的展开图。

以展开图上的10个交点为顶点，画出不同的梯形，并说一说梯形的上底、下底和高各是多少厘米?
参考答案
一、1. 有且只有一组对边平行。

2.
（画法均不唯一）
二、1.C 2.B 3.B
三、(1)× (2)× (3)√ (4)×
四、1．25－6×2－5＝8(cm)
2．略。

四年级数学梯形测试题一、选择题（每题2分，共10分）1. 梯形的定义是什么？A. 只有一组对边平行的四边形B. 四条边都相等的四边形C. 有两组对边相等的四边形D. 有两条边平行的四边形2. 下列哪个图形不是梯形？A. 等腰梯形B. 长方形C. 平行四边形D. 直角梯形3. 如果一个梯形的上底是5厘米，下底是10厘米，高是3厘米，那么这个梯形的面积是多少平方厘米？A. 7.5B. 15C. 22.5D. 304. 梯形的中位线等于两底的什么？A. 平均数B. 差C. 积D. 商5. 下列哪个选项不是梯形的性质？A. 梯形的对角线不相等B. 梯形的中位线平行于两底C. 梯形的对边平行D. 梯形的两对角线相等二、填空题（每题2分，共10分）6. 梯形的面积公式是：________。

7. 如果一个梯形的高是4厘米，上底是6厘米，下底是8厘米，那么它的面积是________平方厘米。

8. 等腰梯形的特点是________。

9. 如果梯形的中位线长度是7厘米，上底是5厘米，那么下底的长度是________厘米。

10. 直角梯形的一个特点是它有________个直角。

三、计算题（每题5分，共10分）11. 一个梯形的上底是4厘米，下底是8厘米，高是3厘米，请计算它的面积。

12. 如果一个梯形的面积是24平方厘米，高是4厘米，上底是5厘米，请计算下底的长度。

四、解答题（每题5分，共10分）13. 一个梯形的上底是6厘米，下底是12厘米，高是5厘米。

如果从这个梯形中去掉一个最大的平行四边形，剩下的部分是什么形状？请计算剩下的部分的面积。

14. 一个等腰梯形的上底是10厘米，下底是20厘米，高是8厘米。

请计算这个等腰梯形的周长。

五、应用题（每题10分，共20分）15. 小明在公园里看到一个梯形的花坛，上底是15米，下底是25米，高是10米。

如果每平方米种植5株花，那么这个花坛可以种植多少株花？16. 一个直角梯形的上底是12厘米，下底是18厘米，高是9厘米。

梯形综合测试题(含答案[经典试卷]第一题:计算下列梯形的面积:梯形ABCD，底边AB为8cm，上底CD为12cm，高h为5cm。

解答:梯形的面积可以通过以下公式计算：$$\text{面积} = \frac{(\text{底边1} + \text{底边2}) \times\text{高}}{2}$$代入已知数值：$$\text{面积} = \frac{(8 + 12) \times 5}{2} = 50 \, \text{cm}^2$$所以，梯形的面积为50平方厘米。

第二题:求下列梯形的高：梯形EFGH，底边EF为6cm，上底GH为10cm，面积为40平方厘米。

解答:梯形的面积可以通过以下公式计算：$$\text{面积} = \frac{(\text{底边1} + \text{底边2}) \times\text{高}}{2}$$已知面积为40平方厘米，底边1为6cm，底边2为10cm。

代入公式，整理求解高：$$40 = \frac{(6 + 10) \times \text{高}}{2} \\80 = (6 + 10) \times \text{高} \\80 = 16 \times \text{高} \\\text{高} = \frac{80}{16} = 5 \, \text{cm}$$所以，梯形的高为5厘米。

第三题:计算下列梯形的周长：梯形IJKL，底边IJ为7cm，上底KL为9cm，高为4cm。

解答:梯形的周长可以通过以下公式计算：$$\text{周长} = \text{底边1} + \text{底边2} + 2 \times \text{高}$$代入已知数值：$$\text{周长} = 7 + 9 + 2 \times 4 = 24 \, \text{cm}$$所以，梯形的周长为24厘米。

第四题:给定梯形面积为60平方厘米，底边1为5cm，底边2为10cm，计算梯形的高。

解答:梯形的面积可以通过以下公式计算：$$\text{面积} = \frac{(\text{底边1} + \text{底边2}) \times\text{高}}{2}$$已知面积为60平方厘米，底边1为5cm，底边2为10cm。

19.3 梯形一、课前预习(5分钟训练)1.下列命题中,是假命题的是( )A.四条边都相等的四边形是菱形B.有三个角是直角的四边形是矩形C.对角线互相垂直平分且相等的四边形是正方形D.一组对边平行,另一组对边相等的四边形是等腰梯形2.如图,四边形ABCD是等腰梯形，AD∥BC，AB=CD，则AC=__________，∠BAD=_________，∠BCD=_________________，等腰梯形这个性质用文字语言可表述为__________________.3.已知等腰梯形的一个内角为100°,则其余三个角的度数分别是____________________.4.如图,等腰梯形ABCD中，AD∥BC，AD=3，AB=4，BC=7，求∠B的度数.二、课中强化(10分钟训练)1.下列四边形中，两条对角线一定不相等的是( )A.正方形B.矩形C.等腰梯形D.直角梯形2.若等腰梯形两底之差等于一腰的长,那么这个梯形一内角是( )A.90°B.60°C.45°D.30°3如图,在等腰梯形ABCD中,AD∥BC,AB≠AD,对角线AC、BD相交于点O.如下四个结论:①梯形ABCD是轴对称图形;②∠DAC=∠DCA;③△AOB≌△DOC;④△AOD∽△BOC.请把其中正确结论的序号填在横线上:____________________.4.观察下图所示图形并填表:5.如图,在等腰梯形ABCD中，AD∥BC，AD=5，AB=6，BC=8，且AB∥DE，则△DEC的周长是( )A.3B.12C.15D.196.如图,已知四边形ABCD中，AB=CD，AC=DB，AD≠BC.求证：四边形ABCD是等腰梯形.7.如图,已知梯形ABCD中，AB∥DC，E是BC的中点，AE、DC的延长线相交于点F，连结AC、BF.(1)求证：AB=CF；(2)四边形ABFC是什么四边形?并说明你的理由.三、课后巩固(30分钟训练)1.下列各命题正确的是( ),2是同类二次根式； B.梯形同一底上的两个角相等A.18C.过一点有且只有一条直线与已知直线平行；D.两条直线被第三条直线所截,同位角相等2.四边形ABCD中,∠A∶∠B∶∠C∶∠D=2∶1∶1∶2,则四边形ABCD的形状是( )A.菱形B.矩形C.等腰梯形D.平行四边形3.如图,在梯形ABCD中,AB∥CD,中位线EF与对角线AC、BD交于M、N两点,若EF=18 cm,MN=8 cm,则AB的长等于( )A.10 cmB.13 cmC.20 cmD.26 cm4.如图,在梯形ABCD中,AD∥BC,CA平分∠BCD,CD=5,则AD的长是( )A.6B.5C.4D.35.如图是一块待开发的土地，规划人员把它分割成①号区、②号区、③号区三块，拟在①号区种花，②号区建房，③号区种树，已知图中四边形ABCD与四边形EFGH是两个相同的直角梯形，则①号区种花的面积是__________________.6.如图,在等腰梯形ABCD中，AD∥BC，AB=CD，且AC⊥BD，AF是梯形的高，梯形面积是49 cm2，则AF=_____________.7.如图,在梯形ABCD中，已知AB∥CD，点E为BC的中点，设△DEA的面积为S1，梯形ABCD的面积为S2，则S1与S2的关系为________________.8.如图,梯形ABCD中，∠ADC=120°，对角线CA平分∠DCB，E为BC的中点，试求△DCE 与四边形ABED面积的比.9.如图,在等腰梯形ABCD中，AB∥CD，AC、BD是对角线，将△ABD沿AB向下翻折到△ABE的位置，试判定四边形AEBC的形状，并证明你的结论.10.如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠ADC=120°.(1)求证:BD⊥DC;(2)若AB=4,求梯形ABCD的面积.11.如图,在等腰梯形ABCD中，AD∥BC，M、N分别为AD、BC的中点，E、F分别是BM、CM的中点.（1）求证：△ABM≌△DCM.（2）四边形MENF是什么图形？请证明你的结论.（3）若四边形MENF是正方形，则梯形的高与底边BC有何数量关系？并请说明理由.参考答案一、课前预习(5分钟训练)1.下列命题中,是假命题的是( )A.四条边都相等的四边形是菱形B.有三个角是直角的四边形是矩形C.对角线互相垂直平分且相等的四边形是正方形D.一组对边平行,另一组对边相等的四边形是等腰梯形答案:D2.如图,四边形ABCD是等腰梯形，AD∥BC，AB=CD，则AC=__________，∠BAD=_________，∠BCD=_________________，等腰梯形这个性质用文字语言可表述为__________________.答案:BD ∠CDA ∠ABC 等腰梯形的对角线相等，等腰梯形同一底上的两个角相等3.已知等腰梯形的一个内角为100°,则其余三个角的度数分别是____________________.答案:80°,80°,100°4.如图,等腰梯形ABCD中，AD∥BC，AD=3，AB=4，BC=7，求∠B的度数.解：过点A作AE∥DC交BC于E.∵AD∥BC，四边形AECD是平行四边形,∴EC=AD=3，DC=AE.∴BE=BC－CE=7－3=4.∵等腰梯形两腰相等，∴CD=AB=4.∴AE=AB=BE=4.∴△ABE是等边三角形.∴∠B=60°.二、课中强化(10分钟训练)1.下列四边形中，两条对角线一定不相等的是( )A.正方形B.矩形C.等腰梯形D.直角梯形解析：由特殊四边形的对角线性质知：正方形、矩形、等腰梯形对角线相等，直角梯形对角线不相等.因此应选D.答案:D2.若等腰梯形两底之差等于一腰的长,那么这个梯形一内角是( )A.90°B.60°C.45°D.30°解析：如图,过点D作DE∥AB,交BC于点E.由已知得出△DEC是等边三角形,所以∠C=60°.答案:B3如图,在等腰梯形ABCD中,AD∥BC,AB≠AD,对角线AC、BD相交于点O.如下四个结论:①梯形ABCD是轴对称图形;②∠DAC=∠DCA;③△AOB≌△DOC;④△AOD∽△BOC.请把其中正确结论的序号填在横线上:____________________.解析：等腰梯形是轴对称图形,所以①对;AD一定不等于CD,所以②错;③④易证正确.所以①③④正确.答案:①③④4.观察下图所示图形并填表:解析：第一个梯形周长是5,后面每增加一个梯形,其周长增加4.答案:21 25 4n+15.如图,在等腰梯形ABCD中，AD∥BC，AD=5，AB=6，BC=8，且AB∥DE，则△DEC的周长是( )A.3B.12C.15D.19解析：由AD∥BC，AB∥DE知四边形ABED为平行四边形,所以AB=DE=6，BE=AD=5.所以EC=BC－BE=8－5=3.故△DEC的周长=6+6+3=15.故应选C.答案:C6.如图,已知四边形ABCD中，AB=CD，AC=DB，AD≠BC.求证：四边形ABCD是等腰梯形.答案:证明：∵AB=DC，AC=DB，BC=CB,∴△ABC≌△DCB（SSS）.∴∠ABC=∠DCB.作AE∥DC交BC于E，则∠1=∠DCB(如图).∴∠ABC=∠1.∴AB=AE.又AB=DC,∴AE=DC.又AE∥DC,∴四边形AECD是平行四边形.∴AD∥BC.又∵AD≠BC，AB=DC，∴四边形ABCD是等腰梯形.7.如图,已知梯形ABCD中，AB∥DC，E是BC的中点，AE、DC的延长线相交于点F，连结AC、BF.(1)求证：AB=CF；(2)四边形ABFC是什么四边形?并说明你的理由.答案: (1)证明：∵AB∥DC，∴∠EAB=∠CFE.∵E 是BC 的中点， ∴CE=BC （中点定义）.又∵∠CEF=∠BEA ，∴△CEF ≌△BEA. ∴AB=CF.(2)解:四边形ABFC 是平行四边形.理由如下:由（1）证明可知，AB 与CF 平行且相等，所以四边形ABFC 是平行四边形. 三、课后巩固(30分钟训练) 1.下列各命题正确的是( )A.18,2是同类二次根式；B.梯形同一底上的两个角相等C.过一点有且只有一条直线与已知直线平行；D.两条直线被第三条直线所截,同位角相等 解析：选项A:2318 ;选项B:应为等腰梯形同一底上的两个角相等; 选项C:应为过直线外一点; 选项D:应为两条平行直线. 答案:A2.四边形ABCD 中,∠A ∶∠B ∶∠C ∶∠D=2∶1∶1∶2,则四边形ABCD 的形状是( )A.菱形B.矩形C.等腰梯形D.平行四边形 解析：∵∠A=∠D,∠B=∠C, ∴四边形ABCD 是等腰梯形. 答案:C3.如图,在梯形ABCD 中,AB ∥CD,中位线EF 与对角线AC 、BD 交于M 、N 两点,若EF=18 cm,MN=8 cm,则AB 的长等于( )A.10 cmB.13 cmC.20 cmD.26 cm 解析：∵EM=FN=21(EF －MN)=5 cm, CD=2EM=10 cm, AB+CD=2EF=36 cm,∴AB=36－CD=26 cm. 答案:D4.如图,在梯形ABCD 中,AD ∥BC,CA 平分∠BCD,CD=5,则AD 的长是( )A.6B.5C.4D.3 解析：∵AD ∥BC,∴∠DAC=∠ACB. ∵CA 平分∠BCD,∴∠ACD=∠ACB. ∵∠DAC=∠ACD,∴AD=CD=5. 答案:B5.如图是一块待开发的土地，规划人员把它分割成①号区、②号区、③号区三块，拟在①号区种花，②号区建房，③号区种树，已知图中四边形ABCD 与四边形EFGH 是两个相同的直角梯形，则①号区种花的面积是__________________.解析：因为四边形ABCD 与四边形EFGH 是两个相同的直角梯形，所以面积相等，即①号区面积+②号区面积=②号区面积+③号区面积，所以①号区面积=③号区面积.由图可知③号区的形状是梯形，其上底为200－4=196 m ，下底是200 m ，高为2 m ，因此面积为21（196+200）×2=396 m 2. 答案:396 m 26.如图,在等腰梯形ABCD 中，AD ∥BC ，AB=CD ，且AC ⊥BD ，AF 是梯形的高，梯形面积是49 cm 2，则AF=_____________.解析：由等腰梯形的性质知AC=BD.平移对角线BD 可得平行四边形AEBD ，从而AE=BD=AC ，EB=AD.因AC ⊥BD,易知∠EAC=90°，再由等腰三角形的三线合一及直角三角形斜边的中线等于斜边的一半可得AF=EC 21=21（EB+BC ）=21（AD+BC ）.根据S 梯形ABCD =21(AD+BC)·AF=AF 2=49，可得AF=7.答案:7 cm7.如图,在梯形ABCD 中，已知AB ∥CD ，点E 为BC 的中点，设△DEA 的面积为S 1，梯形ABCD 的面积为S 2，则S 1与S 2的关系为________________.解析：E 点是BC 的中点，故可延长DE 、AB 相交于点F ，将梯形面积转化为三角形的面积.延长DE 、AB 相交于点F.∵AB ∥CD ，∠C=∠1，∠2=∠F,又CE=BE ，∴△DCE ≌△FBE.∴S △DEC =S △FBE ,DE=EF.因此S △ADE =S △FEB .所以S 梯形ABCD =S △ADF .故S 1=221S . 答案:S 1=221S 8.如图,梯形ABCD 中，∠ADC=120°，对角线CA 平分∠DCB ，E 为BC 的中点，试求△DCE 与四边形ABED 面积的比.解：在梯形ABCD 中，∵AD ∥BC ，AB=DC ，∴∠B=∠DCB ，∠DCB+∠ADC=180°，∠DAC=∠ACB.∵∠ADC=120°，∴∠B=∠DCB=60°.∵CA 平分∠DCB ，∴∠ACB=∠ACD=30°.∴∠B+∠ACB=90°.∴∠BAC=90°.∴AB=BC 21. ∵E 为BC 的中点， ∴BE=CE=BC 21. ∴AB=BE.∵∠DAC=∠ACB=30°，∠ACD=30°，∴AD=DC=AB.∴AD=BE.又∵AD ∥BC ，∴四边形ABED 是平行四边形.设平行四边形ABED 的BE 边上的高是h ，则△DCE 的CE 边上的高也是h. ∴2121=∙∙=∆h BE h CE S S ABED DCE四边形. 9.如图,在等腰梯形ABCD 中，AB ∥CD ，AC 、BD 是对角线，将△ABD 沿AB 向下翻折到△ABE 的位置，试判定四边形AEBC 的形状，并证明你的结论.答案:证明：四边形AEBC 是平行四边形.证明如下：在等腰梯形ABCD 中,∵AB ∥CD ，∴AD=BC ，AC=BD.又∵AB=BA ，∴△ABC ≌△BAD.∴∠ABC=∠BAD.由题意可知△ABE ≌△ABD ，∴AD=AE ，∠BAE=∠BAD.∴AE=BC ，∠BAE=∠ABC ，AE ∥BC.∴四边形AEBC 是平行四边形.10.如图,在梯形ABCD 中,AD ∥BC,AB=DC=AD,∠ADC=120°.(1)求证:BD ⊥DC;(2)若AB=4,求梯形ABCD 的面积.答案:(1)证明:∵AD ∥BC,AB=DC=AD,∴ABCD 是等腰梯形.∴∠BAD=∠ADC=120°,∠ADB=∠ABD=21(180°－∠BAD)=30°. ∴∠BDC=∠ADC －∠ADB=90°.∴BD ⊥DC.(2)解:过点D 作DE ⊥BC 于E,过A 作AF ⊥BC 于F.在Rt △DCE 中,DC=AB=4,∠C=60°,∴DE=DC·sinC=4sin60°=32.∴BC=2CE+EF=2×2+4=8.∴S 梯形ABCD =21×(4+8)×31232 . 11.如图,在等腰梯形ABCD 中，AD ∥BC ，M 、N 分别为AD 、BC 的中点，E 、F 分别是BM 、CM 的中点.（1）求证：△ABM ≌△DCM.（2）四边形MENF 是什么图形？请证明你的结论.（3）若四边形MENF 是正方形，则梯形的高与底边BC 有何数量关系？并请说明理由.答案:（1）证明：∵四边形ABCD 为等腰梯形，∴AB=DC,∠A=∠D.∴AM=DM.∴△ABM ≌△DCM.（2）解：四边形MENF 是菱形.由△ABM ≌△DCM,得MB=MC ，∵E 、F 分别是BM 、CM 的中点，∴ME=BM 21,MF=MC 21,NF=BM 21,NE=MC 21. ∴ME=MF=FN=NE.∴四边形MENF 是菱形.（3）解：梯形的高等于底边BC 的一半，连结MN.∵MENF 是正方形，∴∠BMC=90°.∵MB=MC,N 是中点，∴MN ⊥BC 且MN=BC 21.。