计算马德隆常数

参考文献
[1] 阎守胜.固体物理基础[M].北京：北京大学出版社，2000. [2] Kittle C.固体物理导论[M].北京：科学出版社，1979. [3] 王矜奉.固体物理教程[M].济南：山东大学出版社，2006.
The calculation of Madelung constant in the ion crystal
二维正方离子格子的马德隆常数与对应的 n
30
40
50
1.59236
1.59808
1.60154
1.61554
1.61554
1.61554
100
200
300
1.60851
1.61202
1.61319
1.61554
1.61554
1.61554
800
900
1000
1.61466
1.61476
1.61484
中国科技论文在线

离子晶体的马德隆常数计算
詹泸成，罗志琳
河海大学应用物理系，南京（211100）
E-mail:zhanhucheng@
摘 要:本文对马德隆常数的一般公式进行了修正，并利用 Visual Basic、Matlab 等工具对一 维离子链，二维正方离子格子，以及三维 Nacl 离子晶体修正前后的马德隆常数进行了计算 分析，结果表明：修正后的马德隆常数公式能够更快地收敛于真实值，并且更加接近于实验 值，通过对三个维度的比较，验证了离子晶体马德隆常数随着晶体配位数的增加而增大的性 质。 关键词：离子晶体；马德隆常数；修正 中图分类号：O481
=−
n1 =−n n2 =− n
(−1)n1 + n2 n12 + n22

二维三角离子晶体马德隆常数的计算一、概述二维三角离子晶体的研究在固体物理学领域具有重要意义，其中马德隆常数是一个关键的物理量。

马德隆常数是用来描述晶体中离子间相互作用的强度和类型的参数，对于研究晶体的热力学性质、电子结构和声学性能等方面都具有重要意义。

本文将对二维三角离子晶体马德隆常数的计算进行深入探讨，以期为读者提供有价值的信息。

二、二维三角离子晶体的结构和性质在二维三角离子晶体中，正负电荷的离子按照一定的规则排列在平面上，形成一种特殊的晶体结构。

这种结构具有较强的几何规则性和周期性，因此在研究中具有一定的优势。

二维三角离子晶体的性质受到离子间相互作用的影响很大，而马德隆常数则是描述这种相互作用的重要参数。

三、马德隆常数的定义和物理意义马德隆常数是由英国物理学家马德隆在20世纪初提出的，它是描述晶体中离子间相互作用的参数。

马德隆常数的大小和符号决定了晶体的稳定性和各种物理性质，因此在材料科学研究中具有重要意义。

对于二维三角离子晶体来说，计算马德隆常数可以帮助我们更好地理解晶体结构和性质。

四、马德隆常数的计算方法在实际研究中，计算马德隆常数通常需要借助于复杂的计算方法和理论模型。

一般来说，我们可以通过经典力学或量子力学的理论来建立晶格模型，并在此基础上进行数值计算。

对于二维三角离子晶体来说，由于结构的特殊性，计算方法可能会更加复杂和繁琐。

五、个人观点和理解在我看来，二维三角离子晶体马德隆常数的计算是一个具有挑战性但又具有重要意义的课题。

通过对马德隆常数的准确计算，我们可以更好地理解晶体的结构和性质，为材料科学研究提供重要的参考。

未来，我希望能够进一步深入研究这一课题，为相关领域的发展贡献自己的力量。

六、总结和回顾通过本文的阐述，我们对二维三角离子晶体马德隆常数的计算有了更深入的了解。

马德隆常数作为描述晶体中离子间相互作用的重要参数，对于研究晶体的性质具有重要意义。

未来，我们需要进一步深入研究这一领域，为材料科学的发展做出更大的贡献。

体积是 V０/８.这两种单胞称为互嵌单胞.
如果取氯离子为参考离子,就取氯心单胞为中心单胞,称为第 １
级氯心晶体.
由铯心单胞组成晶体 称 为 铯 心 晶 体,如 图 ２ 所 示,取 ２３ ＝ ８ 个
铯心单胞,组成第 １ 级铯心晶体.第 １ 级铯心晶体嵌套了第 １ 级 氯
图 １ 氯化铯结构的氯心单胞
基本计算方法是累加法,文章提出了氯化铯结构的马德隆常数的累加法公式和递推公式.氯化铯结构有两种不同的表
面,因而有两个不同的累加法的马德隆常数,两个常数都不收敛,其平均值也不代表马德隆常数.埃夫琴采用多个电
中性的埃夫琴单胞组成的晶体,提高了马德隆常数的收敛速度.埃夫琴法实际上是计算晶体内部的离子和内表面离子
５７
言编程,当层数 N 达到 ２００２ 时,结果为 １．
７６２６７４５１８６９３３０２.程序采用三重循环,运行效率肯定不高.
王矜奉等学者 [６]采用双埃夫琴法计算马德隆常数,用 C 语言计算,最好结果是 １．
７６２６７４５.
本文提出了氯化铯晶体的两种互嵌单 胞,阐 明 了 嵌 套 结 构 和 表 面 离 子 的 分 布 规 律,提 出 了 累 加 法 的 递
i
t
y
No．
６Vo
l．
４０
De
c．
２０１９
氯化铯离子晶体的嵌套结构和马德隆
常数的迭代计算
周群益１,莫云飞２∗ ,周丽丽３,侯兆阳４,刘让苏５
(
１．广东技术师范大学 天河学院,广东 广州 ５１０５４０;２．长沙学院 电子信息与电气工程学院,
湖南 长沙 ４１００２２;３．赣南医学院 信息工程学院,江西 赣州 ３４１０００;
氯心单胞,组成第 ２ 级氯心晶体.第 ２ 级氯心晶体嵌套了第 １ 级 铯

计算马德隆常数《固体物理》马德隆常数的计算学院:物理学院学号:2011012643姓名:刘娴雅马德隆常数的计算摘要:通过分析马德隆常数的三种计算方法和其相应的使用范围,得出不同晶体结构下相应的计算方法和使用范围.关键字:马德隆常数离子晶体在固体物理学中,当计算离子晶体的结合能时,需知道马德隆常数的值, 因此,马德隆常数在离子晶体的理论研究和科学实验中占有十分重要的地位.该值一般由实验确定。

马德隆常数是描述离子晶体结构的常数,其定义公式为:n1、n2、n3为离子晶体中任一离子相对于中心离子的坐标,?为求和遍及晶体中所有离子。

由于离子晶体为数目巨大的多粒子系统,因此马德隆常数一般情况下由实验确定。

nnn123,，，，，1,,,, 222nnnn，n，n123123离子晶体结合的性质比较简单,在近代微观理论发展初期，计算离子晶体的结合能获得很好的结果,对于验证理论起到了重要作用,所用的方法和概念在处+-以NaCl为例,由于Na和Cl都是满壳层的结构,具有球对理许多问题中还常用到.称性,考虑库仑作用时,可以看做点电荷.先考虑一个正离子的平均库仑能.如果令r表示相邻离子的距离,该能量可表示为nnn1232，，1q,1，，, (1) 2222222nnn4,,(nr，nr，nr)123012312222222(nr，nr，nr)如果以所考虑的正离子为原点, 可以表示其他各123 离子所占格点的距离,并且对于所有负离子格点，n1+n2+n3=奇数,所有正离子格n1+n2+n3点，n1+n2+n3=偶数.考虑到正负离子电荷的差别,引入因子(-1),一个原胞的能量为，，nnn22123,，，q,1q,,, (2) 222222,,4r4,,rnnn00(nr，nr，nr)123123 nnn123，，,，，1,,, (3) ,222nnnn，n，n123123α为一无量纲的数,完全决定于晶体结构,称之为马德隆常数.在具体计算中发现,求和时既有正项,又有负项,如果逐项相加,并不能得到收敛的结果.对于一维情况,其级数求和很容易计算,如两种一价离子组成的一维晶格的马德隆常数,利用定义很容易计算出α=2ln2,但对于三维情况,其级数收敛很慢. 1918年Madelung首先计算这种级数和,他先将晶体中点阵视为一系列中性平面点阵组成即该平面内点阵由一系列中性直线点阵组成,其上正负电荷相等且按格点周期分布.由此将电势展开成傅里叶级数并用了享克尔函数(Hankel function),进而求出马德隆常数.这种方法对于计算像氯化钠那样简单的离子晶体取得了成功.但对大多数离子晶体而言并不适用。

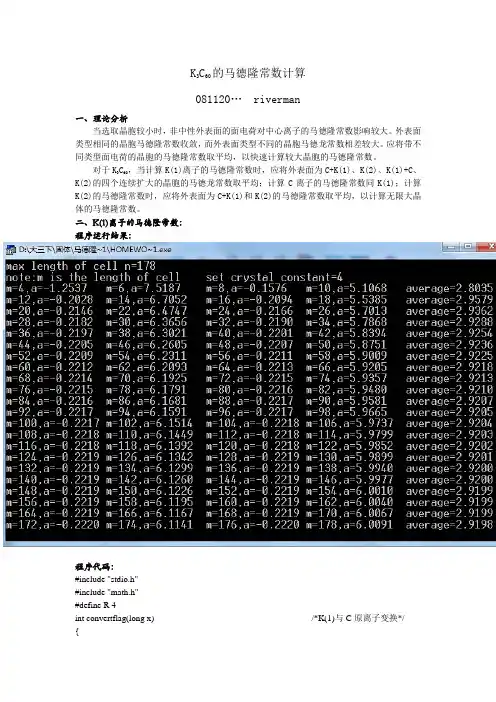
K3C60的马德隆常数计算081120… riverman一、理论分析当选取晶胞较小时，非中性外表面的面电荷对中心离子的马德隆常数影响较大。

外表面类型相同的晶胞马德隆常数收敛，而外表面类型不同的晶胞马德龙常数相差较大。

应将带不同类型面电荷的晶胞的马德隆常数取平均，以快速计算较大晶胞的马德隆常数。

对于K3C60，当计算K(1)离子的马德隆常数时，应将外表面为C+K(1)、K(2)、K(1)+C、K(2)的四个连续扩大的晶胞的马德龙常数取平均；计算C离子的马德隆常数同K(1)；计算K(2)的马德隆常数时，应将外表面为C+K(1)和K(2)的马德隆常数取平均，以计算无限大晶体的马德隆常数。

二、K(1)离子的马德隆常数：程序运行结果：程序代码：#include "stdio.h"#include "math.h"#define R 4int convertflag(long x) /*K(1)与C原离子变换*/ {int flag;if(x%2==1) flag=1;else flag=-3;return flag;}void main(){int n,m,l,i,j,k,flag,n1,n2,n3; /*m为胞长，l半胞长，flag为K(1)和C的电荷数*/long x;/*最外层边长m>=4,正半轴长l>=2*/double r,a=0,ratio=1,b[100]; /*a为马德隆常数*/printf("max length of cell n=");scanf("%d",&n);printf("note:m is the length of cell\tset crystal constant=4\n");for(l=2;l<=n/2;l++){m=2*l;if(l%2==0) /*最外层C+K(1)*/ {/*计算与C+K(1)相互作用*/if(l%4==0) /*最外层顶点同号*/{flag=1; /*顶点电荷*/x=0; /*顶点翻转*/}else /*最外层顶点异号*/{flag=-3; /*顶点电荷*/x=1; /*顶点翻转*/}for(i=-l;i<=l;){n1=i;i+=2;for(j=-l;j<=l;){n2=j;j+=2;for(k=-l;k<=l;){n3=k;k+=2;if(n1*n1+n2*n2+n3*n3==0){flag=convertflag(x++);continue;}r=sqrt(n1*n1+n2*n2+n3*n3);if(n1==l||n1==-l) ratio=ratio/2;if(n2==l||n2==-l) ratio=ratio/2;if(n3==l||n3==-l) ratio=ratio/2;a+=-flag/r*ratio*R;/*printf("(%d,%d,%d)\tflag=%d\tratio=%f\ta=%f\n",n1,n2,n3,flag,ratio,a);*/flag=convertflag(x++);ratio=1;}}}/*计算与K(2)相互作用*/for(i=-l+1;i<=l-1;){n1=i;i+=2;for(j=-l+1;j<=l-1;){n2=j;j+=2;for(k=-l+1;k<=l-1;){n3=k;k+=2;r=sqrt(n1*n1+n2*n2+n3*n3);a+=-1/r*R;/*printf("(%d,%d,%d)\ta=%f\n",n1,n2,n3,a);*/}}}}else /*最外层K(2)*/ {/*与计算K(2)相互作用*/for(i=-l;i<=l;){n1=i;i+=2;for(j=-l;j<=l;){n2=j;j+=2;for(k=-l;k<=l;){n3=k;k+=2;r=sqrt(n1*n1+n2*n2+n3*n3);if(n1==l||n1==-l) ratio=ratio/2;if(n2==l||n2==-l) ratio=ratio/2;if(n3==l||n3==-l) ratio=ratio/2;a+=-1/r*ratio*R;/*printf("(%d,%d,%d)\tratio=%f\ta=%f\n",n1,n2,n3,ratio,a);*/ratio=1;}}}/*计算与C+K(1)相互作用*/if((l-1)%4==0) /*次外层顶点同号*/ {flag=1;x=0;}else /*次外层顶点异号*/ {flag=-3;x=1;}for(i=-l+1;i<=l-1;){n1=i;i+=2;for(j=-l+1;j<=l-1;){n2=j;j+=2;for(k=-l+1;k<=l-1;){n3=k;k+=2;if(n1*n1+n2*n2+n3*n3==0){flag=convertflag(x++);continue;}r=sqrt(n1*n1+n2*n2+n3*n3);a+=-flag/r*R;/*printf("(%d,%d,%d)\tflag=%d\ta=%f\n",n1,n2,n3,flag,a);*/flag=convertflag(x++);ratio=1;}}}}…………若干}getch();}三、C离子的马德隆常数程序运行结果：程序代码：程序与计算K(1)类似，省略相同部分，划线部分为代码差别之处。

高等固体物理作业题 目: 马德隆常数的计算方法及实例计算 学生姓名： 学 院：理学院 专 业：物理电子学 指导教师:2013 年 12 月 7日学校代码：10128 学 号：摘要在固体物理学中，当计算离子晶体的结合能、晶格能、表面能等时，需知道马德隆常数的值，该值一般由实验确定。

马德隆常数是描述离子晶体结构的常数，是晶体结构的一个重要的特征参数，为一无量纲的数，只取决于晶体结构，在离子晶体的研究中占有重要的地位。

本文概述了晶体马德隆常数的几种计算方法及其使用范围，并举例简述了一维离子链，二维正方离子格子，以及三维Nacl离子晶体实例的马德隆常数的计算方法。

关键词：离子晶体；马德隆常数；计算方法；实例AbstractIn solid state physics, when calculate the combined energy, attice energy, surface energy, etc. of the ionic crystals, we need to know the Madelung constant value, which is generally determined by experiment. Madelung constant is used to describe structure of ionic crystal. Madelung constant is an important feature of the crystal structure parameters. Madelung constant is a dimensionless number that only depends on the crystal structure, and plays an important role in the study of ionic crystals. This article outlines several crystal Madelung constant calculation methods and its scope of application, and an example calculation methods outlined Madelung constant one-dimensional ion chains, two-dimensional square lattice ions, as well as three-dimensional Nacl ionic crystals instance.Keywords: ionic crystals; Madelung constant; calculation methods; examples目录引言 (1)1 晶体马德隆常数的几种计算方法 (2)1.1 定义法 (2)1.2 Evjen晶胞法 (2)1.3 计算晶格静电能法 (3)1.4 小结 (4)2 马德隆常数的实例计算 (5)2.1 一维离子链的马德隆常数计算 (5)2.2 二维正方离子格子的马德隆常数计算 (6)2.3 三维离子晶体（Nacl）的马德隆常数计算 (7)参考文献 (10)引 言马德隆(Madelung)常数α是晶体结构中的一个重要的特征参数，是描述粒子晶体结构的常数。

马德隆常数计算公式
马德隆常数是一种重要的数学常数，常用于计算圆周率π的近似值。

这个常数由英国数学家约翰·马德隆（John Madelaune）于1706年推导出来，因此得名。

马德隆常数的计算公式相对简单，可以通过以下式子得出：M = ∑(4/((2n-1)(2n+1))), 其中n从1开始递增，一直累加到无穷大为止。

通过这个公式，我们可以逼近得到π的值。

然而，马德隆常数不同于其他常数的地方在于它的收敛速度非常缓慢。

换句话说，要通过计算马德隆常数来得到π的精确值，需要进行无数次的累加运算。

这使得计算过程非常繁琐，甚至对于现代计算机而言也是一个巨大的挑战。

尽管马德隆常数在计算圆周率方面的应用存在一定的困难，但它在数值计算和近似计算领域仍然有着重要的意义。

它可以作为一种近似计算π的方法，尤其适用于没有高精度计算设备的时代。

在缺乏现代计算工具的情况下，数学家们通过手工计算马德隆常数，得到了种种与π相关的近似值，为后来的研究和计算提供了重要的基础。

此外，马德隆常数还引发了数学上的一些有趣问题和研究方向。

例如，我们可以探究该常数的收敛速度，研究如何加速计算马德隆常数以及优化近似π的方法等等。

这些问题激发了众多数学家的兴趣，并催生了一系列关于马德隆常数的研究成果。

总而言之，马德隆常数是一个重要而有趣的数学常数，虽然计算过程繁琐但在近似计算π和数值计算中仍然有一定的应用价值。

它不仅是对历史上数学家们智慧的体现，也激发了更多关于近似计算和数值分析的研究。

（4）
根据公式（3）（4），编程计算（附录
2），得出得到
α
2
，
α
' 2
与
n
的对应关系，如下
表：
n
10
α2 1.54824
α2’
1.61541
n
80
α2 1.60676
α2’
1.61554
n
600
α2 1.61437
α2’
1.61554

表2 20 1.58105 1.61553 90 1.60773 1.61554 700 1.61453 1.61554
Zhan Lucheng,Luo Zhilin
Department of Physics, HoHai University, Nanjing (211100)
Abstract This paper amended the Madelung constant’s formula,then calculated and analysised the Madelung constant of one-dimensional ion,two-dimensional ion and three-dimensional ion crystal with Visual Basic and Matlab.The result was that the amended formula of Madelung constant could go to the truth more quickly and be closer to the truth. In addition,with the comparision of three kinds of crystal,we proved that Madelung constant increased when the coordination number of crystal increased. Keywords: ion crystal;Madelung constant;amend

两粒子间的相互作用力f(r)和相互作用势能u(r)随粒子间距r变化 的一般关系如图
1：两粒子间的相互作用势能u(r) 两粒子间的相互作用势能u(r),可用下面的表达式表示
1：两粒子间的相互作用力
二. 晶体的结合能
Eb 为负值，表示晶体的能量比构成晶体的粒子处在自由状态时 的能量总和低。 Eb 的绝对值就是把晶体分离成自由原子所需要 的能量。Eb 也称为晶体的总相互作用能。
3：离子晶体：由正离子和负离子组成。
4：
二：基本特征
1. 离子晶体的模型：正、负离子—— 刚球 化合物：NaCl， CsCl是典型的离子晶体，晶体结
构如图所示。一种离子的最近邻离子为异性离子，离子 晶体的配位数最多只能是8（例如CsCl 晶体）。氯化钠 配位数是6。
2. 离子结合的特征
（1）离子键的形成 以 NaCl 为例 ，在凝聚成固体时，Na 原子失去
离子间的相互作用分为两大类：吸引作用和排斥作用。 (1) 静电引力，即正、负离子之间的库仑作用力（又称为 离子键；异极键）。
离子键无方向性和饱和性: 与任何方向的电性不同的离 子相吸引，所以无方向性；且只要是正负离子之间，则彼 此吸引，即无饱和性。
(2) 由于泡利不相容原理，两个离子的闭合壳层电子云的交 迭产生强大的排斥力； —— 排斥力和吸引力相互平衡时，形成稳定的离子晶体。
F
+－+－+－+－
－+－+－+－+
位错
+－+－+－+－ －+－+－+－+
受力时发生错位，使正正离子相切，负负离子相切，彼此排 斥，离子键失去作用，故离子晶体无延展性 。如 CaCO3 可 用于 雕刻，而不可用于锻造，即不具有延展性 。

——例 ——例1：计算二维NaCl晶格的马德隆常数 计算二维NaCl晶格的马德隆常数
1. 一个埃夫琴晶胞的计算（如图） 一个埃夫琴晶胞的计算（如图）
设参考离子o为正离子， 设参考离子 为正离子，则4个位于边中间的负离子对参考 为正离子 个位于边中间的负离子对参考 离子的库仑作用为： 离子的库仑作用为： 1 4× 2 1 4个位于顶角的正离子对参考离子的库仑 个位于顶角的正离子对参考离子的库仑 作用为： 作用为： 1 4× 4 − 2 一个埃夫琴晶胞的马德隆常数为： 一个埃夫琴晶胞的马德隆常数为：
1. 一个埃夫琴晶胞的计算（如图） 一个埃夫琴晶胞的计算（如图） 设参考离子o为正离子。 设参考离子 为正离子。 为正离子 负离子对参考离子的库仑作用为： 负离子对参考离子的库仑作用为： 1 1 8× 6× 8 2+ 1 3 正离子对参考离子的库仑作用为： 正离子对参考离子的库仑作用为： 1 12× 4 − 2 一个埃夫琴晶胞的马德隆常数为： 一个埃夫琴晶胞的马德隆常数为：
2. 32个埃夫琴晶胞的计算（如图） 个埃夫琴晶胞的计算（如图）
所有负离子的库仑作用为: 所有负离子的库仑作用为
4 ×1 8 ×1 4 ×1 / 2 8 ×1 / 2 + + + 1 3 5 13
所有正离子的库仑作用为: 所有正离子的库仑作用为
4 ×1 4 ×1 4 ×1 8 ×1 / 2 4 ×1 / 4 − − − − − 2 2 8 10 18
附录2.1： 附录2.1： 离子晶体马德隆常数的计算方法
由公式
α =−∑
n1 n 2 n 3
/
(−1) n1 + n2 + n3
2 (n1 + n2 + n ) 2 1 2 2 3

一维准晶马德隆常数刘玉鑫(渭南师范学院 物理与电气工程学院 物理学 2010级1班）摘 要：回顾准晶体的发展应用，了解准晶的发展前景，简述准晶结构的的特征，物理性质，介绍马德隆常数及其重要意义和基本计算方法，介绍两种斐波那契类准晶结构的计算方法，通过构建一维准晶结构模型计算斐波那契类准晶结构的马德隆常数，从而对准晶体及其重要性有基本的认识，加深对马德隆常数的进一步理解应用。

关键词：一维准晶体结构特征；马德隆常数；斐波那契类；点阵模型随着人们对准晶结构的认识越来越深入，准晶的重要价值也在被人们更多的发展应用，而马德隆常数作为晶体结构的重要特征参数，利用马德隆常数可计算晶体表面能和晶格能、结合能等重要物理量，尽管现今未发现属于离子晶体的准晶体材料，但准晶体材料大部分由金属合金组成而金属键中含有离子键成份，因此本文在介绍准晶结构的基础上对一维准晶的马德隆常数进行计算。

从而对准晶材料有更好的认识，并为准晶材料的利用提供参考价值。

1 准晶及其结构特征1.1 什么是准晶准晶也就是准周期晶体［1～2］。

它是由以色列科学家谢切曼等人在1984年第一次发现的一种介于晶体与非晶体之间的特殊固态物质结构。

是一种即在长程准周期上有序，又具有非晶体学旋转对称性的固态的有序物态相，它是一种最新发现的固态结构。

1.2 准晶体物质的物理特征准晶体材料物质由于其在就结构方面的特殊性，使得其具有晶体所没有的一些性质。

1.2.1 传输特性在准晶物质已知的所有的物理性能中，它的电子传输特性是最特殊和最重要的[1]。

它主要体现在以下三个方面：导电性：(1）相较于普通的金属间化合物，热力学稳定的准晶物质的电阻率要高出许多。

例如准晶相Li Cu Al --，它全部是由非过渡元素族组成的，当在液氦温度时，它的的电阻率为 900 cm Ωμ。

相较于准晶相(含有过渡元素族），它的电阻率就更高了。

例如Ru Cu Al --准晶在同样温度下电阻率是1000 ~30000cm μ，Fe Cu Al --准晶体是 1300~11000 cm Ωμ ，Mn Pd Al -- 则为1000 ～9500cm Ωμ。

二维NaCl晶体马德隆常数计算--双埃夫琴晶胞唐为民【摘要】以正方晶胞作为计算单元,并以该晶胞的中心为原点,采用双埃夫琴晶胞方法得到二维NaCl晶体马德隆常数的计算公式.通过C语言编程计算其马德隆常数的值.【期刊名称】《闽南师范大学学报：自然科学版》【年(卷),期】2019(032)001【总页数】4页(P51-54)【关键词】二维NaCl;晶体;双埃夫琴晶胞;马德隆常数【作者】唐为民【作者单位】[1]闽南师范大学物理与信息工程学院,福建漳州363000;【正文语种】中文【中图分类】O481马德隆常数是在计算离子晶体库仑能时引入的一个无量纲的参数，可表示为[1]式中“±”表示为同号离子取“-”，异号离子取“+”；ɑj是以最近邻离子间距r0为单位的第j个离子到参考离子的距离，因此，马德隆常数是一个仅与晶体结构有关的参数．为了计算马德隆常数，1932年Evjen提出了一种比较简单有效的计算方法[2]，即把晶体看成由许多完全相同的晶胞（埃夫琴晶胞）组成，每个晶胞保持电中性，取一个晶胞的中心离子为参考离子，它和其它所有离子的库仑作用可分为本晶胞内离子的作用及其他晶胞离子的作用．当晶胞取足够大时，其它晶胞与参考离子距离较远，且电中性，因此对参考离子的作用可以忽略，即只需考虑本晶胞内离子作用．该方法计算NaCl晶体尤为有效，收敛速度极快．后来，刘策军，王永杰采用埃夫琴晶胞法计算了二维NaCl离子晶体的马德隆常数[3-4]．对于CsCl晶体，像这样取一个埃夫琴晶胞来计算，并不能得到收敛值，主要原因是这样取埃夫琴晶胞会造成两种不同情况，即最外层离子与参考离子都同号或者都异号，而这两种情况计算值完全不同，王矜奉提出用两个体积相近的埃夫琴晶胞（双埃夫琴晶胞）计算CsCl晶体马德隆常数的方法[5]．本文分析二维NaCl晶体的结构特点，采用双埃夫琴晶胞法来计算其马德隆常数．1 二维NaCl晶体结构分析及马德隆常数计算式图1是二维NaCl晶体点阵，为正方结构．以中心的“Cl”为参考离子，有两种不同的晶胞取法：一种如图中的实线所取（亦即文献[3][4]所采用的方法），其特点是晶胞的最外层的“Na”和“Cl”总是相间排列的，这和三维NaCl特点相同；另一种是图中的虚线所取，当取最小晶胞时，其最外层都是“Na”，与参考离子不同，而取次小晶胞时，最外层则都为“Cl”，依此类推，第三小晶胞最外层为“Na”，第四小晶胞最外层为“Cl”，……，此特点与文献[5]计算的三维CsCl晶体（图2所示）相似，因此可采用双埃夫琴晶胞，即本文所用方法．图1 二维NaCl晶体两种晶胞的选法Fig.1 Two selection methods for unitcells of two-dimensional NaCl图2 CsCl晶体晶胞Fig.2 Unit cell of CsCl crystal以埃夫琴晶胞的中心参考离子作为坐标原点，建立 xOy坐标系，如图3所示，图中显示到第四层离子（共由“4×4”个最小晶胞组成）．设两个同种离子最近邻的距离为2a，这样参考离子至最近邻离子的距离为而任一离子至参考离子的距离可表示为式中n1是以 a为单位 x轴的坐标，n2是以 a为单位 y轴的坐标，于是式（1）中的 aj为从图中可以看出离子的位置要求n1，n2只能同时为奇数或者同时为偶数，但不能同时为零，而且同时取奇数时对应的离子与参考离子异号，同时取偶数时则为同号．因此式（1）可写成式中的n为所取晶胞的层数（整个晶胞由“n×n”个最小晶胞组成）．考虑到最外层四个顶点上的离子是由四个晶胞共同所有，因此每个顶点离子对马德隆常数贡献1/4，同理最外层四条棱上的离子（除顶点外）贡献1/2，其余离子处在晶胞内部，贡献为1．考虑到晶胞的对称性，可以把晶胞内部的所有离子分成四块完全等价的区域，如图4所示，只需计算其中一块区域然后乘于4即可，同理最外层的四个顶点、四条棱上的离子也等价的，也只需算其中之一然后乘于4．因此，当取埃夫琴晶胞的总层数为n时，马德隆常数为式中第一项为晶胞内部离子的贡献，n1，n2只取同奇偶性；第二项为最外层棱上离子（顶点除外）的贡献，n1只取和 n相同奇偶性；第三项为顶点离子贡献．根据双埃夫琴晶胞法的思想，可得二维NaCl离子晶体马德隆常数计算式图3 以晶胞中心离子为坐标原点各离子在直角坐标下的位置分布Fig.3 Ion distribution in Cartesian coordinate taking the central ion of unit cell as itsorigin图4 晶胞中的离子分为等价的4块区域Fig.4 Four equivalent divided areas of ions in its unit cell2 计算结果及讨论根据式（6）、（7）采用C语言（数值用双精度）进行编程计算，表1给出了α随 n变化的计算结果．从表1中可以看出α的值随所取晶胞的层数n的增大而增大，并且当n较小时α值变化较大，而当n取值越大时，α变化越小，最后趋于收敛．因此，当晶胞取得足够大时（约 n=500），可以得到二维NaCl晶体马德隆常数大约为1.615 54，这与文献里采用单个埃夫琴晶胞得到的值1.613 843[3]（计算到 n=8 000）和 1.615 542 626 712 96[4]（计算到 n=10 000）相近．表1 二维NaCl离子晶体马德隆常数α计算值Tab.1 Calculated values of Madelung constant(α)of two-dimensional NaCl crystaln 3 α 1.577 178 859 n α 55 1 0001.615 380 342 7 1.606 770 362 75 1.615 454 923 11 1.611 783 197 100 1.615 492 127 15 1.613 467 933 200 1.615 530 064 19 1.614 230 289 300 1.615 537 053 23 1.614 638 467 500 1.615 540 623 27 1.614 882 125 700 1.615 541 604 35 1.615 146 116 55 1 000 1.615 542 1263 结论以晶胞的中心离子作为参考离子，采用双埃夫琴晶胞的方法并借助C语言编程计算了二维NaCl离子晶体的马德隆常数α．计算结果表明数值随所取晶胞的增大而增大，并且当晶胞越大时α变化越缓慢，最后大约稳定在1.615 54，此结果与文献值相近，说明二维NaCl离子晶体马德隆常数在适当选取晶胞后，可以用单埃夫琴晶胞计算，也可以用双埃夫琴晶胞计算．参考文献：【相关文献】[1]吴代鸣.固体物理学[M].长春：吉林大学出版社，1996.[2]H.M.Evjen.Stability of Certain Heteropolar Crystals[J].Physical Review，1932，39(4)：675-687.[3]刘策军.二维NaCl晶体马德隆常数计算[J].大学物理，1995，14(12)：21-22.[4]王永杰，赵占龙.NaCl晶体的马德隆常数计算[J].保定学院学报，2007，20(4)：19-20.[5]王矜奉，朱露莎，邓桂昌，等.采用双Evjen晶胞计算离子晶体的马德隆常数[J].四川师范大学学报(自然科学版)，2001，24(5)：471-474.。

二维三角离子晶体马德隆常数的计算在计算二维三角离子晶体马德隆常数时，首先需要了解马德隆常数的概念。

马德隆常数是二维晶格的一个重要物理性质，它描述了二维晶体的刚性和弹性特性。

马德隆常数可以通过实验测量得到，也可以通过理论计算得到。

在这篇文章中，我们将深入探讨二维三角离子晶体马德隆常数的计算方法和意义。

1. 二维三角离子晶体的结构特点1.1 二维三角离子晶体的晶格结构二维三角离子晶体是由正负电荷离子组成的晶格结构，其晶格平面的排列呈现出三角形的几何形状。

在晶格结构中，正负电荷离子相互排列，形成一定的周期性和对称性。

1.2 二维三角离子晶体的物理性质二维三角离子晶体具有独特的物理性质，包括机械性能、光学性能以及电学性能等。

这些物理性质与晶格结构密切相关，同时也与马德隆常数有着内在的联系。

2. 马德隆常数的物理意义2.1 马德隆常数的定义马德隆常数是描述晶体的弹性特性的物理参数，它反映了晶体在受到应力作用时的形变程度。

对于二维三角离子晶体来说，马德隆常数是衡量其弹性变形能力的重要参数。

2.2 马德隆常数的意义马德隆常数的大小和数值表达了晶体对应力的敏感程度和应变的程度，它直接影响着晶体的力学性能和稳定性。

通过计算二维三角离子晶体的马德隆常数，可以深入理解其力学和弹性特性。

3. 二维三角离子晶体马德隆常数的计算方法3.1 理论计算方法通过理论模型和密度泛函理论等方法，可以对二维三角离子晶体的晶格结构进行建模，并通过量子力学计算得到马德隆常数的理论数值。

3.2 实验测量方法利用X射线衍射、红外光谱等实验方法，可以测量二维三角离子晶体在受力作用下的晶体结构变化，从而得到马德隆常数的实验数值。

4. 我对二维三角离子晶体马德隆常数的个人观点和理解在我看来，二维三角离子晶体马德隆常数的计算不仅是对其物理性质的深入探究，更是对纳米材料力学性能的理解和探索。

通过对马德隆常数的计算和分析，可以为纳米材料的设计和应用提供重要参考。

一维准晶马德隆常数刘玉鑫(渭南师范学院物理与电气工程学院物理系 10级1班) 摘要：回顾准晶体的发展应用，了解准晶的发展前景，简述准晶结构的的特征，物理性质，介绍马德龙常数及其重要意义和基本计算方法，介绍两种斐波那契类准晶结构的计算方法，通过构建一维准晶结构模型计算斐波那契类准晶结构的马德龙常数，从而对准晶体及其重要性有基本的认识，对马德龙常数进一步理解应用。

关键词：一维准晶体结构特征；马德隆常数；斐波那契类；点阵模型随着人们对准晶结构的认识越来越深入，准晶的重要价值也在被人们更多的发展应用，而马德龙常数作为晶体结构的重要特征参数，利用马德隆常数可计算晶体表面能和晶格能、结合能等重要物理量，尽管现今未发现属于离子晶体的准晶体材料，但准晶体材料大部分由金属合金组成而金属键中含有离子键成份，因此本文在介绍准晶结构的基础上对一维准晶的马德龙常数进行计算。

从而对准晶材料有更好的认识，并未准晶材料的利用提供参考价值。

1 准晶及其结构特征1.1 什么是准晶准晶也就是准周期晶体。

它是由以色列科学家谢切曼等人在1984年第一次发现的一种介于晶体与非晶体之间的特殊固态物质结构。

是一种即在长程准周期上有序，又具有非晶体学旋转对称性的固态的有序物态相，它是一种最新发现的固态结构。

1.2 准晶体物质的物理特征准晶体材料物质由于其在就结构方面的特殊性，使得其具有晶体所没有的一些性质。

1.2.1 传输特性在准晶物质已知的所有的物理性能中，它的电子传输特性是最特殊和最重要的。

它主要体现在以下三个方面：导电性（1）相较于普通的金属间化合物，热力学稳定的准晶物质的电阻率要高出许多。

例如准晶相x1- Cu- Li，它全部是由非过渡元素族组成的，当在液氦温度时，它的的电阻率为 900 μΩcm。

相较于准晶相（含有过渡元素族），它的电阻率就更高了。

例如xl- Cu- Ru准晶在同样温度下电阻率是1000 ~30000μcm，xl- Cu- Fe 准晶体是 1300~11000 μΩcm ，x1- Pd- Mn 则为1000 ～9500μΩcm。

32埃夫琴晶胞的马德隆常数为： 埃夫琴晶胞的马德隆常数为：
4 ×1 4 ×1 4 ×1 8 ×1 / 2 4 ×1 / 4 4 ×1 8 ×1 α =− − − − − + + 2 1 2 8 10 18 5 4 ×1 / 2 8 ×1 / 2 + + = 1.611 3 13
——例 ——例2：计算三维NaCl晶格的马德隆常数 计算三维NaCl晶格的马德隆常数
2
4 ×1 / 2 4 ×1 / 4 − 2 8 4 ×1 4 ×1 / 2 4 ×1 / 4 所有正离子的库仑作用为: − 所有正离子的库仑作用为 − − 2 2 8 2埃夫琴晶胞的马德隆常数为： 2 埃夫琴晶胞的马德隆常数为： 4 ×1 8 ×1 / 2 4 ×1 4 ×1 / 2 4 ×1 / 4 α= + − − − = 1.607 1 2 5 2 8
一个埃夫琴晶胞
α=
4×
1 1 4× 2− 4 = 1.293 1 2
2. 22个埃夫琴晶胞的计算（如图） 个埃夫琴晶胞的计算（如图）
4个近邻负离子对参考离子的库仑作用为： 4×1 1 个近邻负离子对参考离子的库仑作用为： 个近邻负离子对参考离子的库仑作用为 1 8个边中间负离子的库仑作用为 8× / 5 个边中间负离子的库仑作用为: 个边中间负离子的库仑作用为 2 4 ×1 8 ×1 / 2 + 所有负离子的库仑作用为: 所有负离子的库仑作用为 1 5 4个近邻正离子的库仑作用为： − 4× 1 个近邻正离子的库仑作用为： 个近邻正离子的库仑作用为 8个边界正离子的库仑作用为 − 个边界正离子的库仑作用为: 个边界正离子的库仑作用为
2. 32个埃夫琴晶胞的计算（如图） 个埃夫琴晶胞的计算（如图）

二维ＮａＣｌ晶体马德隆常数计算刘策军（华南农业大学基础课部广州５１０６４２）摘要通过计算机运算，给出二维ＮａＣｌ晶体马德隆常数的计算结果．关键词二维ＮａＣｌ晶体；马德隆常数分类号Ｏ４８１引言晶体结合问题中，要涉及离子晶体结合能概念．在离子晶体结合能计算中，马德隆常数（ＭａｄｅｌｕｎｇＣｏｎ－ｓｔａｎｔ）α是一个重要物理量．最典型的离子晶体是ＮａＣｌ型晶体，其马德隆常数的定义是￣［１－４］上式中取第ｉ个离子为参考离子，Ｎ为正负离子总数，求和时与参考离子同号的取负号，异号的离子取正号．α＿ｊ是以最近邻离子间距为单位的第ｊ个离子距参考离子的距离；α值完全由晶体结构所决定．本文在对一维和三维ＮａＣｌ晶体马德隆常数研究结果的基础上，分析给出二维情况下ＮａＣｌ晶体（１）式求和的计算表达式，然后给出由计算机算出的结果，最后与一维和三维情况的α值进行比较．２二锥ＮａＣｌ晶体α计算求和表达式为解决（１）式求和收敛的问题，历史上曾发展了几种有效的计算α的方法．本文采用一种比较简单而直观的方法￣［２，３］．设想把晶体分成许多大的晶胞，平均每个晶胞所含正、负离子数相同，整个晶胞保。

《固体物理》马德隆常数得计算学院：物理学院学号：20１1０12６43姓名：刘娴雅马德隆常数得计算摘要:通过分析马德隆常数得三种计算方法与其相应得使用范围，得出不同晶体结构下相应得计算方法与使用范围、关键字：马德隆常数离子晶体在固体物理学中，当计算离子晶体得结合能时，需知道马德隆常数得值, 因此,马德隆常数在离子晶体得理论研究与科学实验中占有十分重要得地位、该值一般由实验确定.马德隆常数就是描述离子晶体结构得常数，其定义公式为：n1、n2、n3为离子晶体中任一离子相对于中心离子得坐标，∑为求与遍及晶体中所有离子。

由于离子晶体为数目巨大得多粒子系统,因此马德隆常数一般情况下由实验确定。

离子晶体结合得性质比较简单，在近代微观理论发展初期，计算离子晶体得结合能获得很好得结果，对于验证理论起到了重要作用,所用得方法与概念在处理许多问题中还常用到、以NaCl为例，由于Ｎa+与Cl-都就是满壳层得结构,具有球对称性,考虑库仑作用时，可以瞧做点电荷、先考虑一个正离子得平均库仑能、如果令r表示相邻离子得距离，该能量可表示为（1）如果以所考虑得正离子为原点, 可以表示其她各离子所占格点得距离，并且对于所有负离子格点，ｎ１＋n2＋n3＝奇数，所有正离子格点，ｎ１＋ｎ２+ｎ３＝偶数、考虑到正负离子电荷得差别，引入因子(—１)n１＋n2＋n3，一个原胞得能量为(2）(３）α为一无量纲得数,完全决定于晶体结构，称之为马德隆常数、在具体计算中发现，求与时既有正项，又有负项，如果逐项相加，并不能得到收敛得结果、对于一维情况，其级数求与很容易计算,如两种一价离子组成得一维晶格得马德隆常数，利用定义很容易计算出α=2ln2,但对于三维情况，其级数收敛很慢、１91８年Mａｄelｕnｇ首先计算这种级数与，她先将晶体中点阵视为一系列中性平面点阵组成即该平面内点阵由一系列中性直线点阵组成，其上正负电荷相等且按格点周期分布、由此将电势展开成傅里叶级数并用了享克尔函数（Hankｅｌｆunct ｉon)，进而求出马德隆常数、这种方法对于计算像氯化钠那样简单得离子晶体取得了成功、但对大多数离子晶体而言并不适用。