线性规划原问题与对偶问题的转化及其应用
- 格式:doc
- 大小:2.14 MB
- 文档页数:21

线性规划对偶问题线性规划是一种优化问题的数学建模方法,在实际生产和管理中广泛应用。
线性规划问题通常包括最大化或最小化一个线性目标函数的约束条件下的一组线性不等式或等式。
对于一个线性规划问题,其对偶问题是通过对原问题的目标函数和约束条件进行变换而得到的。
对偶问题有助于理解原问题的特性,并提供关于原问题的附加信息。
具体来说,对于一个原问题:最小化 C^T * X约束条件 A * X >= bX >= 0其中,C是目标函数的系数矩阵,X是决策变量向量,A是约束条件的系数矩阵,b是约束条件的右侧向量。
对于原问题的对偶问题,其形式为:最大化 b^T * Y约束条件 A^T * Y <= CY >= 0其中,Y是对偶变量向量。
对偶问题的最优解被称为对偶可行解,对偶问题的最优解与原问题的最优解之间存在弱对偶性和强对偶性。
弱对偶性指的是对于原问题的任意可行解X和对偶问题的任意可行解Y,有C^T * X >= b^T * Y。
这意味着对于原问题的任意最优解X*和对偶问题的任意最优解Y*,有C^T * X* >=b^T * Y*。
强对偶性指的是如果原问题和对偶问题的任意一个都有有界解,那么它们必然存在一对最优解,使得C^T * X* = b^T * Y*。
对偶问题的解决可以通过使用单纯形法或内点法等优化算法来进行求解。
对偶问题对线性规划问题的求解具有重要的应用价值和理论意义。
它可以用于确定原问题的可行解的界限,还可以提供原问题的敏感性分析和稳定性分析。
总之,线性规划的对偶问题是通过对原问题的目标函数和约束条件进行变换而得到的,对偶问题为理解原问题的特性和提供附加信息提供了一种有力的工具。


目录1. 原问题和对偶问题的定义2. 最优解的概念和求解方法3. 原问题和对偶问题最优解的关系4. 应用举例5. 结论1. 原问题和对偶问题的定义在数学和优化领域,原问题和对偶问题是一对相关的问题,它们通常是相互关联的,并且在求解过程中起到互补的作用。
原问题是指在优化理论中所要解决的实际问题,通常以最大化或最小化某个目标函数为目标,同时满足一系列约束条件。
上线性规划中,原问题可以表示为:Maximize(或Minimize):C^T*xSubject to:Ax ≤ b其中C和x分别为目标函数系数和决策变量,A和b则表示约束条件。
而对偶问题则是通过原问题的构造,利用拉格朗日对偶性得到的一个与原问题等价的问题。
对偶问题通常与原问题具有相同的最优解,在某些情况下,对偶问题甚至比原问题更容易求解。
对偶问题的一般形式可以表示为:Minimize:b^T * ySubject to:A^T * y ≥ C其中y为对偶变量,A^T为A的转置。
2. 最优解的概念和求解方法我们需要定义最优解的概念。
在数学和优化领域中,最优解通常指的是在给定条件下能够最大化或最小化一个特定目标函数的解。
上线性规划中,最优解即为能够最大化或最小化目标函数的决策变量取值。
为了求解原问题和对偶问题的最优解,通常可以采用不同的优化算法,如线性规划中的单纯形法、内点法等。
这些算法能够根据问题的特点和约束条件,有效地寻找到最优解。
3. 原问题和对偶问题最优解的关系在优化理论中,原问题和对偶问题之间存在着一种重要的对偶关系。
具体来说,对偶问题的最优解可以与原问题的最优解相互通联,满足一定的关系。
对于原问题的最优解x*和对偶问题的最优解y*,它们之间存在着强对偶性(strong duality)的关系。
强对偶性是指下面的不等式成立:C^T * x* ≤ b^T * y*A^T * y* ≥ C这个关系意味着原问题和对偶问题的最优解是互相约束的,当原问题的最优解达到最大值时,对偶问题的最优解也能达到最小值,反之亦然。

用对偶单纯形法求解线性规划问题对偶单纯形法是一种常用于求解线性规划问题的方法。
它通过对原始线性规划问题进行对偶化,将原问题转化为对偶问题,并通过迭代的方式逐步优化,最终得到最优解。
本文将详细介绍对偶单纯形法的基本原理和步骤,并通过一个实例来演示其具体应用。
对偶单纯形法的基本原理是基于线性规划的对偶性理论。
根据对偶性理论,对于原始线性规划问题的最优解,一定存在一个对偶问题,其最优解与原问题的最优解相等。
因此,我们可以通过求解对偶问题来得到原问题的最优解。
对偶问题的形式如下:最大化 W = b'y约束条件为:A'y ≤ c其中,A是原始线性规划问题的约束矩阵,b是原始问题的目标函数系数矩阵,c是原始问题的约束条件矩阵,y是对偶问题的变量向量。
对偶单纯形法的步骤如下:步骤1: 初始化将原始线性规划问题转化为标准型,并初始化基变量和非基变量的初始解。
步骤2: 计算对偶变量值根据对偶问题的约束条件,计算对偶变量的初始值。
步骤3: 计算对偶目标函数值根据对偶问题的目标函数,计算初始的对偶目标函数值。
步骤4: 检验最优性判断当前解是否为最优解。
如果是,则终止算法;否则,进入下一步。
步骤5: 选择入基变量和出基变量根据当前解,选择一个入基变量和一个出基变量。
步骤6: 更新解通过列生成法或其他方法,更新当前解。
步骤7: 更新对偶变量和对偶目标函数值根据更新后的解,更新对偶变量和对偶目标函数值。
步骤8: 转至Step 4重复步骤4至步骤7,直到找到最优解。
下面以一个具体的线性规划问题为例来演示对偶单纯形法的应用。
假设有以下线性规划问题:最大化 Z = 3x1 + 5x2约束条件为:2x1 + x2 ≤ 10x1 + 3x2 ≤ 15x1, x2 ≥ 0首先,将原始问题转化为标准型:最大化 Z = 3x1 + 5x2约束条件为:2x1 + x2 + s1 = 10x1 + 3x2 + s2 = 15x1, x2, s1, s2 ≥ 0初始化基变量和非基变量的初始解为:x1 = 0, x2 = 0, s1 = 10, s2 = 15根据对偶问题的约束条件,计算对偶变量的初始值:y1 = 0, y2 = 0根据对偶问题的目标函数,计算初始的对偶目标函数值:W = 0检验最优性,发现当前解不是最优解,需要进入下一步。
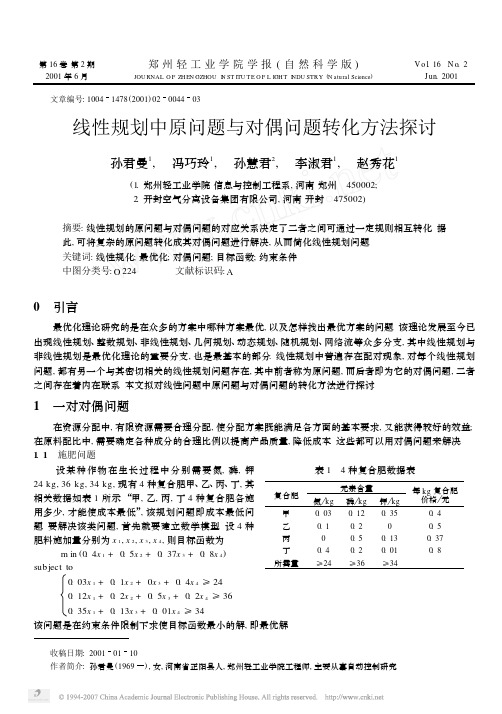
文章编号:10041478(2001)02004403收稿日期:20010110 作者简介:孙君曼(1969),女,河南省正阳县人,郑州轻工业学院工程师,主要从事自动控制研究.第16卷第2期 郑州轻工业学院学报(自然科学版) V o l.16 N o .22001年6月JOU RNAL O F ZH EN GZHOU I N ST ITU TE O F L IGH T I N DU STRY (N atural Science )Jun .2001线性规划中原问题与对偶问题转化方法探讨孙君曼1, 冯巧玲1, 孙慧君2, 李淑君1, 赵秀花1(1.郑州轻工业学院信息与控制工程系,河南郑州 450002;2.开封空气分离设备集团有限公司,河南开封 475002)摘要:线性规划的原问题与对偶问题的对应关系决定了二者之间可通过一定规则相互转化.据此,可将复杂的原问题转化成其对偶问题进行解决,从而简化线性规划问题.关键词:线性规化;最优化;对偶问题;目标函数;约束条件中图分类号:O 224 文献标识码:A0 引言最优化理论研究的是在众多的方案中哪种方案最优,以及怎样找出最优方案的问题.该理论发展至今已出现线性规划、整数规划、非线性规划、几何规划、动态规划、随机规划、网络流等众多分支,其中线性规划与非线性规划是最优化理论的重要分支,也是最基本的部分.线性规划中普遍存在配对现象,对每个线性规划问题,都有另一个与其密切相关的线性规划问题存在,其中前者称为原问题,而后者即为它的对偶问题,二者之间存在着内在联系.本文拟对线性问题中原问题与对偶问题的转化方法进行探讨.1 一对对偶问题在资源分配中,有限资源需要合理分配,使分配方案既能满足各方面的基本要求,又能获得较好的效益;在原料配比中,需要确定各种成分的合理比例以提高产品质量,降低成本.这些都可以用对偶问题来解决.1.1 施肥问题表1 4种复合肥数据表复合肥元素含量氮 kg 磷 kg 钾 kg 每kg 复合肥价格 元甲0.030.120.350.4乙0.10.200.5丙00.50.130.37丁0.40.20.010.8所需量≥24≥36≥34 设某种作物在生长过程中分别需要氮,磷,钾24kg,36kg,34kg,现有4种复合肥甲、乙、丙、丁,其相关数据如表1所示.“甲,乙,丙,丁4种复合肥各施用多少,才能使成本最低”,该规划问题即成本最低问题.要解决该类问题,首先就要建立数学模型.设4种肥料施加量分别为x 1,x 2,x 3,x 4,则目标函数为 m in (0.4x 1+0.5x 2+0.37x 3+0.8x 4)sub ject to 0.03x 1+0.1x 2+0x 3+0.4x 4≥240.12x 1+0.2x 2+0.5x 3+0.2x 4≥360.35x 1+0.13x 3+0.01x 4≥34该问题是在约束条件限制下求使目标函数最小的解,即最优解.1.2 效益最佳问题设某公司生产单肥,氮、磷、钾元素的相关数据同表1.要解决怎样制订这3种单肥价格以获得最大效益的问题,也要首先建立数学模型.设氮、磷、钾订价分别为y 1,y 2,y 3,则目标函数为 m ax (24y 1+36y 2+34y 3)sub ject to0.03y 1+0.12y 2+0.35y 3≤0.40.1y 1+0.2y 2≤0.50.5y 2+0.13y 3≤0.370.4y 1+0.2y 2+0.01y 3≤0.8该问题是在4个约束条件限制下,求使目标函数最大的解,即最优解.上述施肥问题与效益最佳问题即是一对对偶问题,二者可相互转化,且目标函数值是统一的.若2个问题的目标函数分别为W ,Z ,则目标函数如图1所示.2 对偶问题的表达形式2.1 对称形式的对偶原问题 m in CX 对偶问题 m ax YBsub ject to A X ≥B sub ject to YA ≤CX ≥0Y ≥0其中,A =(P 1,…,P n )是m ×n 矩阵;B =(b 1,…,b m )T 是m 维列向量;C =(c 1,…,c n )是n 维向量;X =(x 1,…,x n )T 是由原问题的变量组成的n 维列向量;Y =(y 1,…,y m )是由对偶问题的变量组成的m 维行向量.2.2 非对称形式的对偶原问题 m in CX 对偶问题 m ax YB sub ject to A X =B sub ject to YA ≤CX ≥0该形式的对偶在原问题中有1个等式约束,且对偶问题中m 个变量均无正负号限制.2.3 一般形式的对偶原问题 m in CX 对偶问题 m ax (Y 1B 1+Y 2B 2+Y 3B 3)sub ject toA 1X ≥B 1sub ject to Y 1A1+Y 2A 2+Y 3A 3≤CA 2X =B 2Y 1≥0A 3X ≤B 3Y 3≤0X ≥0Y 2无限制其中,A 1是m 1×n 矩阵;A 2是m 2×n 矩阵;A 3是m 3×n 矩阵;B 1,B 2,B 3分别是m 1,m 2,m 3维列向量;C 是n 维行向量;X 是n 维列向量;Y 1,Y 2,Y 3分别是由变量组成的m 1,m 2,m 3维行向量.3 原问题与对偶问题的转化规则原问题与对偶问题是相对的,二者为同类型的规划,构成对偶规划的一般规则如下:1)若原问题是极大化问题,那么对偶问题就是极小化问题;若原问题是极小化问题,那么对偶问题就是极大化问题.2)在原问题与对偶问题中,约束右端向量与目标函数中系数恰好对换.3)对于极小化问题的“≥”型约束(极大化问题的“≤”型约束),相应的对偶变量有非负限制;对于极小化问题的“≤”型约束(极大化问题的“≥”型约束),相应的对偶变量有非正限制;对于原问题的“=”型约束,相应的对偶变量无正负限制.4)对于极小化问题的具有非负限制的变量(极大化问题的具有非正限制的变量),在其对偶中相应的约束为“≤”型不等式;对于极小化问题的具有非正限制的变量(极大化问题的具有非负限制的变量),在其对偶问题中相应的约束为“≥”型不等式;对于原问题中无正负限制的变量,在其对偶问题中相应的约束为・54・ 第2期孙君曼等:线性规划中原问题与对偶问题转化方法探讨 等式.4 原问题与对偶问题的转化实例化对偶问题 m ax Z =x 1+3x 2sub ject to x 1+2x 2≤5①x 2≤3②x 1,x 2≥0设对应约束条件①②的对偶变量分别为y1,y 2,则 m in W =5y 1+3y 2 sub ject to y 1≥12y 1+y 2≥3y 1,y 2≥0化对偶问题 m in Z =2x 1+3x 2-5x 3+x 4sub ject to x 1+x 2-3x 3+x 4≥5③2x 1+2x 3-x 4≤4④x 2+x 3+x 4=6⑤x 1≤0,x 2,x 4≥0,x 3可取任意值设对应约束条件③④⑤的对偶变量分别为y 1,y 2,y 3,则有 m ax W =5y 1+4y 2+6y 3 sub ject to y 1+2y 2≤2y 1+y 3≥3-3y 1+2y 2+y 3=-5y 1-y 2+y 3≥1y 1≥0,y 2≤0,y 3可取任意值值得注意的是,原问题决策变量的符号决定了对偶问题约束条件的符号,原问题约束条件的符号决定了对偶问题决策变量的符号.5 结论正确写出原问题的对偶问题后,可根据二者之间的关系以及单纯形法、对偶单纯形法、Karm arkar 算法等求解方法较方便地解出线性规划问题.参考文献:[1] 钱松迪.运筹学[M ].北京:清华大学出版社,2000.48—61.[2] 陈宝林.最优化理论与算法[M ].北京:清华大学出版社,2000.156—169.D iscussion on the conversion m ethods of problem anddual problem i n li near programm i ngSU N Jun 2m an 1Κ FEN G Q iao 2ling 1Κ SU N H u i 2jun 2Κ L I Shu 2jun 1Κ ZHAO X iu 2hua 1;1.D ep t .of Inf or m a tion and Con trolling E ng .ΨZ heng z hou Inst .of L ig h t Ind .ΨZ heng z hou 450002ΨCh ina [2.K a if eng A ir S ep a rap ion G roup Co .ΨL td .ΨK a if eng 475002ΨCh ina ΓAbstract ΠT he co rresponding relati on betw een the p rob lem and dual p rob lem determ ines that the tw o p rob lem s can be tran sfo rm ed betw een each o ther by certain ru les .So Κthe com p lex p rob lem can be sovled th rough its dual p rob lem Κand the linear p rogramm ing is p redigested .Key words Πlinear p rogramm ing Μop ti m izati on Μdual p rob lem Μob jective functi on Μcon strain t conditi on・64・ 郑州轻工业学院学报(自然科学版)2001年 。

原问题和对偶问题解的关系
原问题和对偶问题是线性规划中的两个重要概念,它们之间有着密切的联系。
在线性规划中,我们通常会遇到以下两种问题:
1. 原问题:是指需要我们求解的线性规划问题,通常是一个最
大化或最小化的目标函数,同时满足一些线性等式或不等式约束条件。
2. 对偶问题:是指与原问题相关的一个线性规划问题,它的目
标函数和约束条件与原问题相反,通常也是一个最大化或最小化的目标函数,同时满足一些线性等式或不等式约束条件。
原问题和对偶问题之间的关系可以概括为以下几点:
1. 对于任意一个线性规划问题,都存在一个与之相关的对偶问题。
2. 原问题的最优解和对偶问题的最优解具有一定的对偶关系,
也就是说,如果原问题的最优解为x,对偶问题的最优解为y,那么
x和y之间存在一种对偶关系,即x和y满足一些特定的约束条件。
3. 对于任意一个线性规划问题,其原问题和对偶问题的最优解
是相等的,即原问题的最优解等于对偶问题的最优解。
4. 原问题和对偶问题之间的对偶关系不仅可以帮助我们求解线
性规划问题,还可以帮助我们理解线性规划问题的本质和内在结构。
通过以上几点,我们可以看出,原问题和对偶问题之间的关系非常密切,它们不仅可以相互推导和求解,还可以帮助我们更好地理解和应用线性规划问题。
- 1 -。
对偶问题的原理和应用1. 对偶问题的概述对偶问题是线性规划领域的一个重要概念,它通过将原始问题转化为对偶形式,从另一个角度来解决问题。
对偶问题在优化领域有着广泛的应用,尤其在线性规划中起到了重要的作用。
2. 对偶问题的原理对偶问题的转化是基于线性规划的标准形式进行的。
假设我们有一个原始线性规划问题:最小化:c T x约束条件:$Ax \\geq b$ 变量约束:$x \\geq 0$其中,c是目标函数的系数向量,A是约束矩阵,b是约束条件的右侧常数向量。
对于原始问题,我们可以定义一个对偶问题。
对偶问题的定义如下:最大化:b T y约束条件:$A^Ty \\leq c$ 变量约束:$y \\geq 0$其中,y是对偶问题的变量向量。
对偶问题的目标函数和约束条件是原始问题的线性组合,并且满足一定的对偶性质。
3. 对偶问题的求解方法对偶问题的求解方法有两种:一种是通过求解原始问题得到对偶问题的最优解,另一种是通过求解对偶问题得到原始问题的最优解。
这两种方法都可以有效地解决线性规划问题。
3.1 原始问题到对偶问题的转换原始问题到对偶问题的转换可以通过拉格朗日对偶性定理来实现。
该定理表明,原始问题的最优解与对偶问题的最优解之间存在一种对偶性关系。
通过求解原始问题的对偶问题,我们可以获得原始问题的最优解。
3.2 对偶问题到原始问题的转换对偶问题到原始问题的转换可以通过对偶定理来实现。
该定理表明,对偶问题的最优解与原始问题的最优解之间存在一种对偶性关系。
通过求解对偶问题,我们可以获得原始问题的最优解。
4. 对偶问题的应用对偶问题在实际应用中具有广泛的应用,下面介绍几个常见的应用场景。
4.1 线性规划问题对偶问题在线性规划中得到了广泛的应用。
通过将原始问题转化为对偶形式,我们可以使用对偶问题的求解方法来求解线性规划问题。
对偶问题可以提供原始问题的最优解,并且可以帮助我们理解原始问题的性质和结构。
4.2 经济学和管理学对偶问题在经济学和管理学中也有重要的应用。
原问题和对偶问题解的关系
原问题和对偶问题是线性规划中的两个重要概念。
原问题是寻找一组变量的最优解,使得满足一组约束条件和目标函数最优化。
而对偶问题是将原问题的约束条件和目标函数进行转换,得到一个新的问题,通过求解该问题得到原问题的下界或上界。
原问题和对偶问题解之间有着紧密的联系和关系。
具体来说,如果原问题有最优解,那么对偶问题也有最优解,并且两者的最优解相等。
这被称为“强对偶定理”。
此外,如果原问题
的某个可行解不是最优解,则对偶问题的最优解就是原问题的最优解。
这被称为“弱对偶定理”。
原问题和对偶问题解的关系可以用下面的公式来表示:
原问题的最优解 = 对偶问题的最优解 = 原问题的最优值 = 对
偶问题的最优值
这个公式表明,原问题和对偶问题的最优解是等价的,它们都可以用来解决同一个线性规划问题。
因此,在实际应用中,我们可以选择任何一个问题来求解,但是需要注意的是,有些情况下一个问题的求解比另一个问题更容易,更高效。
因此,在实际应用中,我们需要根据具体问题的特点来选择问题。
- 1 -。
线性规划原问题与对偶问题的转化及其应用摘要线性规划对偶问题是运筹学中应用较广泛的一个重要分支,它是辅助人们进行科学管理的一种数学方法.线性规划对偶问题能从不同角度为管理者提供更多的科学理论依据,使管理者的决定更加合理准确.本文主要探讨了线性规划原问题与对偶问题之间的关系、线性规划原问题与对偶问题的转化以及对偶理论的应用.本文的研究主要是将复杂的线性规划原问题转化成对偶问题进行解决,简化了线性规划问题,使人们能够快速的找出线性规划问题的最优解.关键词:线性规划;原问题;对偶问题;转化Linear Programming is the Original Problem and the Transformation ofthe Dual Problem and ApplicationsAbstract: Linear programming in operational research is research earlier, rapid development and wide application, the method is an important branch of mature, it is one of the scientific management of auxiliary people mathematical method. Can from different angles to linear programming dual problem for policy makers to provide more scientific theory basis. This article mainly probes into the linear programming problem and the relationship between the dual problem, linear programming problem and the transformation of the dual problem, the application of linear programming dual problem. This article is the complex of the original problem into its dual problem to be solved, simplifies the linear programming problem, enables us to rapidly find the optimal solution of linear programming problem.Keywords: linear programming; the original problem; the dual problem; conversion目录1 引言 (1)2 文献综述 (1)2.1国内外研究现状 (1)2.2国内外研究现状评价 (2)2.3提出问题 (2)3 预备知识 (2)3.1对称形式的原问题 (2)3.2非对称形式的原问题 (3)3.3对偶问题的定义 (3)3.4原问题转化为对偶问题的理论依据 (4)4 原问题与对偶问题的转化 (5)4.1原问题与对偶问题的关系 (5)4.2对称型原问题化为对偶问题 (6)4.3对称型对偶问题转换为原问题 (9)4.4非对称型原问题转化为对偶问题 (10)4.5对偶问题的应用 (13)5 结论 (15)5.1主要发现 (15)5.2启示 (15)5.3局限性 (15)5.4努力方向 (15)参考文献 (15)1 引言线性规划问题是运筹学里的一个重要的分支,它的应用比较广泛,因而是辅助人们进行现代科学管理的一种数学方法.随着线性规划理论的逐步深入,人们发现线性规划问题具有对偶性,即每一个线性问题都伴有另外一个线性问题的产生,两者相互配对,密切联系,反之亦然.我们把线性规划的这个特性称为对偶性.于是,我们将其中的一个问题称为原问题,另一个问题则称为它的对偶问题.对偶性不仅仅是数学上的理论问题,而且也是线性规划中实际问题的内在经济联系的必然反映.我们通过对对偶问题的深入研究,发现对偶问题能从不同角度对生产计划进行分析,从而使管理者能够间接地获得更多比较有用的信息.2 文献综述2.1 国内外研究现状在所查阅到的国内外参考文献[1-15]中,有不少文章是探讨了原问题转化为对偶问题的方法以及对偶性质的证明,并在对偶理论的应用方面有所研究.如郝英奇,胡运权在[1]、[10]中主要介绍了线性规划中原问题与对偶问题中的一些基本概念,探究了实际问题中的数学模型以及解.孙君曼,冯巧玲,孙慧君,李淑君等在[2]中探讨了对偶理论中互补松弛定理在各种情况下的使用方法,使学生更好地掌握互补松弛定理的含义和应用方法.胡运权,郭耀煌,殷志祥等在[3]、[5]中系统的介绍了线性规划中原始问题与对偶问题的两种形式.郭鹏,徐玖平等在[6]、[8]中用不同例子来说明了原问题转化为对偶问题的必要性. 崔永新等在[9]、[15]中探讨了对偶问题的相关定理以及对偶问题的可行解和最优解之间的若干性质.李师正,王德胜在[11]中探讨了如何用计算机计算对偶问题的最优解.岳宏志,蔺小林,孙文喻等在[12]、[14]中探讨了对偶理论的证明过程,并用常见的例子来说明对偶理论的基本思想和解题方法. 曾波,叶宗文在[13]中主要从经济管理的实际问题中阐述了线性规划的基本概念,基本原理,对偶理论,灵敏度分析等.2.2 国内外研究现状评价文献[1-15]分别探讨了线性规划问题中原问题转化为对偶问题的理论依据以及如何利用对偶理论去解决实际生产问题.文献中主要探讨了对称型的原问题转化为对偶问题的方法.没有全面介绍非对称型的原问题与对偶问题之间转化的具体步骤,而且文献中对原问题转化为对偶问题的步骤提及甚少,大都一带而过,对应用中存在的问题也未给出详细深入的说明.2.3 提出问题在线性规划问题中,根据实际生产中具体情况的需要,我们常常要把原问题与它的对偶问题进行转换,以解决一些复杂的线性规划问题,因而对偶问题的应用较为广泛.但大部分书籍都只介绍了线性规划问题的基础知识,并没有给出原问题与对偶问题转换的具体步骤.因此本文主要探讨了线性规划原问题与对偶问题之间转化的具体步骤,体会不同类型原问题的转化过程.3 预备知识首先我先简单的介绍一些关于线性规划问题中的原问题和对偶问题的一些基本的知识.3.1对称形式的原问题我们将满足下列条件的线性规划问题称之为具有对称形式的线性规划问题.这类问题的变量都具有非负约束,当目标函数求极大值时,它的约束条件都取“≤”号,当目标函数求极小值时它的约束条件均取“≥”号. 因而,这类数学模型的特点是:(1)所有的决策变量都是非负的;(2)所有的约束条件都是“≤”型;(3)目标函数是最大化类型.线性规划原问题的对称形式的]1[一般形式为:n n x c x c x c z +++= 2211m ax⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥≤+++≤+++≤+++),,2,1(0.22112222212111212111n j x b x a x a x a b x a x a x a b x a x a x a t s j m n mn m m n n n n (3.1)3.2 非对称形式的原问题不是所有的线性规划问题都具有对称的形式,我们将没有对称形式的线性规划问题称之为非对称形式的线性规划问题.非对称形式的线性规划问题指的是一般情况下的线性规划问题,即是目标函数值求极小或者求极大;约束条件;,或是无限制的随意的组合.例如:332211m ax x c x c x c z ++= ⎪⎪⎩⎪⎪⎨⎧≤≥≤++=++≤++无约束321333323213123232221211313212111,0,0.x x x b x a x a x a b x a x a x a b x a x a x a t s (3.2)3.3 对偶问题的定义在运筹学中,关于对线性规划的对偶规划给出的]2[定义如下.设给定的线性规划为:CX z =max⎩⎨⎧≥≤0.X b AX t s (3.2) 其中()T n x x x X ,,,21 =,()nm ij a A ⨯=,()T m b b b b ,,,21 =,()n c c c C ,,,21 = 因此,定义它的对偶问题为:Yb w =min⎩⎨⎧≥≥0.Y C YA t s (3.4) 其中()m y y y Y ,,,21 =是行向量. (3.4)是对偶问题,(3.3)是原问题,(3.3)与(3.4)合在一起我们就称为是一对对称形式的对偶规划问题.3.4原问题转化为对偶问题的理论依据我们根据线性规划问题中约束条件和变量的对应关系,统一归纳为下]3[1表所示:表14 原问题与对偶问题的转化一对对偶的线性规划问题表示了同一个问题的两个侧面,是从两个角度对同一个研究对象提出的极值问题,两类极值的问题都具有相同的目标函数值.我们发现在很多时候求解对偶问题比原问题更加容易,为决策者提供更多的科学理论依据,因此我们常常需要把原问题转化为对偶问题.4.1原问题与对偶问题的关系一对对偶的线性规划问题具有相互对应的关系:(1)原问题中的目标函数值是max ,约束条件是“≤”的形式;对偶问题的min 目标函数值为,”约束条件是“≥的形式.(2)原问题的价值系数和对偶问题的右端项对应,原始问题的右端项和对偶问题的价值系数对应.(3)原问题的变量和对偶问题的约束条件对应,即,原问题中有个n 变量,那么对偶问题就有个n 约束条件;原问题有个m 约束条件,那么对偶问题就有个m 变量.(4)对偶问题的系数矩阵就是原问题的系数矩阵的转置.用矩阵表示,原问题为:CX z =max⎩⎨⎧≥≤0..X b AX t s 则对偶问题为:Yb w =min⎩⎨⎧≥≥0..Y C YA t s 需要注意的是,我们所讨论的对偶问题一定是指一对问题,而原问题和对偶问题是相对的,它们互为对偶问题,一个问题可以是原问题也可以是对偶问题.4.2 对称型原问题转化为对偶问题当线性规划问题为一般形式(3.1)时,我们将根据下面的四条规则转换为它的对偶问题:(1)原问题和它的对偶问题之间的系数矩阵互为转置.(2)原问题中变量的个数等于它的对偶问题的约束条件的个数.(3)原问题的右端常数就是对偶问题的目标函数的系数.(4)原问题的目标函数求极大时,约束条件是“≤”类型,而它的对偶问题的目标函数求极小,约束条件则为“≥”类型.因此,它的对偶问题可以转变为如下的]4[形式:m m y b y b y b w +++= 2211m in⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥≥+++≥+++≥+++),,1(0..22112222211211221111n i y c y a y a y a c y a y a y a c y a y a y a t s i n m mn n n m m m m例1 生产计划问题云南一公司加工生产甲,乙两种产品,它的市场前景非常的好,销路也不成问题,各种制约因素主要有技术工人、设备台时和原材料供应.已知制造每吨产品的资源消耗系数、每天的资源限量和售价等参数如表2所示.问题:云南的这家公司应该怎样制定每天的生产计划,才能使它的产量得到最大?表2 分析:为了建立此问题的数学模型,第一,要选定决策变量.第二,要确定问题的目标,即用来评价不同方案优劣的标准,这种目标总是决策变量的函数,称为目标函数.第三,我们把要确定达到目标时所受的限制条件,称之为约束条件.这里要决策的问题是,在现有人力、设备、矿石的限制下,如何确定产量使得产值自大?设1x 和2x 分别表示该公司A ,B 产品的数量,用z 表示产值,则每天的产值表示为2115090x x z +=,使其最大化,即2115090m ax x x z +=,称为目标函数.将制约因素表达出来,即有:人力不超过320工时,为3206821≤+x x ;设备不超过260台时有,2608621≤+x x ;原材料不超过300公斤有,30010421≤+x x 。