角的度量与表示和角的比较相关练习题

数学角的度量试题1.量出∠1的度数并标明．【答案】【解析】用量角器量出角的度数再在图上标明即可．解：∠1的度数为40°，如图，．点评：本题主要考查角的度量，正确画图很关键．2.先量出两个角的度数，再比较大小．【答案】30°，＜，70°【解析】用量角器的圆点和角的顶点重合，0刻度线和角的一条边重合，另一条边在量角器上的刻度就是该角的度数．解：测量结果如下：故答案为：30°，＜，70°点评：本题主要考查了学生测量角的能力．3.已知两个长方形按如图所示的方式叠放，下图中的∠1和∠2是否相等？说明理由．【答案】∠1和∠2相等，因这两个角与∠3的和都是90°【解析】根据题意知∠1和∠3组成了一个直角，∠2和∠3组成了一个直角，让∠1和∠2分别用∠3和90°的关系表示，再进行比较．解：∠1+∠3=90°，∠1=90°﹣∠3，∠2+∠3=90°，∠2=90°﹣∠3，所以：∠1=∠2．答：∠1和∠2相等，因这两个角与∠3的和都是90°．点评：本题的关键是通过中间的量∠3来表示∠1和∠2，再时行比较．4.计算下列时刻的时针与分针所形成角的度数．（1）10点20分（2）7点36分（3）3点50分．【答案】（1）10点20分时针与分针所形成的角的度数是160°（2）7：36时针与分针所形成的角的度数是12°（3）3点50分时针与分针所形成的角的度数是175°【解析】因为钟表上的刻度是把一个圆平均分成了12等份，每一份是30°，借助图形，找出时针和分针之间相差的大格数，用大格数乘30°即可．时针每小时转一个大空格即30°，所以每分钟转30°÷60=0.5°，分针每分钟转个大空格，即30°×=6°，由此进行解答即可．解：因为时针在钟面上每分钟转0.5°，分针每分钟转6°，（1）钟表上10点20分时，时针与分针的夹角可以看成时针转过10时0.5°×20=10°，分针在数字4上．因为钟表12个数字，每相邻两个数字之间的夹角为30°，所以10点20分时分针与时针的夹角5×30°+10°=160°．答：10点20分时针与分针所形成的角的度数是160°；（2）钟表上7点36分时，时针与分针的夹角可以看成时针转过7时0.5°×36=18°，分针在数字7过一格上．所以7点36分时分针与时针的夹角18°﹣6°=12°．答：7：36时针与分针所形成的角的度数是12°．（3）钟表上3点50分时，时针与分针的夹角可以看成时针转过3时0.5°×50=25°，分针在数字10上．因为钟表12个数字，每相邻两个数字之间的夹角为30°，所以3点50分时分针与时针的夹角5×30°+25°=175°．答：3点50分时针与分针所形成的角的度数是175°．点评：本题考查钟表分针所转过的角度计算．在钟表问题中，常利用时针与分针转动的度数关系：分针每转动1°时针转动（）°，并且利用起点时间时针和分针的位置关系建立角的图形．5.填一填．（1）测量角的大小用；度量角的单位是，用符号“”表示，把半圆平均分成180份．每一份所对的角的大小是．（2）看量角器上的刻度，把各个角的度数写下来．【答案】（1）测量角的大小用量角器；度量角的单位是度，用符号“°”表示，把半圆平均分成180份．每一份所对的角的大小是1°．（2）各个角的度数如下图：【解析】（1）根据测量角的工具，以及单位，及单位的成因进行解答．（2）用量角器的圆点和角的顶点重合，0刻度线和角的一条边重合，另一条边在量角器上的刻度就是该角的度数．可量出角的度数．解：（1）测量角的大小用量角器；度量角的单位是度，用符号“°”表示，把半圆平均分成180份．每一份所对的角的大小是1°．（2）各个角的度数如下图：点评：本题主要考查了学生对测量角方法的掌握情况，注意要看清是角的一条边是和量角器的内圈的还是外圈的0刻度线对齐．6.观察下面两个角的大小，再量一量，你有什么结论？结论：．【答案】角的大小和角两边的长短无关．【解析】角的大小角的大小和角的两边叉开的大小有关，张口越大，角越大；张口越小，角越小，角的大小和角两边的长短无关．依此即可作答．解：测量可知，两个角的度数都是50°，可得结论：角的大小和角两边的长短无关．故答案为：角的大小和角两边的长短无关．点评：考查了角的大小与角的两边张开的大小有关，与边的长短无关的知识点．7.请你把下面图形的四个角的度数量出来．你发现了什么？（1）图1：∠1=∠2=∠3=∠4=（2）图2：∠1=∠2=∠3=∠4=（3）图3：∠1+∠4=∠2+∠3=．【答案】50°，130°，50°，130°；65°，115°，65°，115°；180°，180°【解析】先把量角器放在角的上面，使量角器的中心和角的顶点重合，零度刻度线和角的一条边重合，角的另一条边所对的量角器上的刻度，就是这个角的度数．依此量出各角，再作答．解：测量可知：（1）图1：∠1=50°，∠2=130°，∠3=50°，∠4=130°；（2）图2：∠1=65°，∠2=115°，∠3=65°，∠4=115°；（3）图3：∠1+∠4=55°+125°=180°，∠2+∠3=55°+125=180°．故答案为：50°，130°，50°，130°；65°，115°，65°，115°；180°，180°．点评：此题主要考查角的度量和四边形的内角和等于360°的性质．8.请你用一张正方形的纸折出45°和135°的角．并把你的作品贴在下面．【答案】【解析】因为正方形四个角都是直角，所以将正方形沿对角线对折一次就可以得到90°÷2=45°角；因为135度角=90°+45°，所以先将正方形上下对折，左右对折，再沿得到的小正方形沿对角线对折就可以得到135度角．解：如图所示：．点评：此题主要考查学生的动手能力和空间想象能力．9.在三角形ABC中，一个锐角是30°．截去这个角后（如图），剩下图形的内角和是多少度？【答案】剩下图形的内角和是360°【解析】根据三角形的内角和是180度，可求出∠A和∠C角的度数的和，再求出∠ADE的度数．再加上90，就是这个剩下图形内角和的度数．据此解答．解：∠A+∠C=180°﹣30°=150°，∠BDE=180°﹣30°﹣90°=60°，∠ADE=180°﹣∠BDE=180°﹣60°=120°，四边形的内角和是：∠A+∠C+∠ADE+∠CED，=150°+120°+90°，=360°．答：剩下图形的内角和是360°．点评：本题的主要考查了学生根据三角形内角和是180度的知识解答问题的能力．10.量出下面各角的度数．【答案】60°，110°，170°【解析】用量角器的圆点和角的顶点重合，0刻度线和角的一条边重合，另一条边在量角器上的刻度就是该角的度数．解：测量结果如下：故答案为：60°，110°，170°．点评：本题主要考查了学生用量角器测量角的能力．11.先估计，再量一量，填一填．（1）∠1=（2）∠1=∠2=∠3=∠1+∠2+∠3=（3）∠1=∠2=∠3=∠4=∠1+∠2+∠3+∠4=．【答案】40°，60°，90°，30°，180°，60°，120°，60°，120°，360°【解析】用量角器的圆点和角的顶点重合，0刻度线和角的一条边重合，另一条边在量角器上的刻度就是该角的度数．解：测量结果如下：（1）∠1=40°（2）∠1=60°∠2=90°∠3=30°∠1+∠2+∠3=180°（3）∠1=60°∠2=120°∠3=60°∠4=120°∠1+∠2+∠3+∠4=360°．故答案为：40°，60°，90°，30°，180°，60°，120°，60°，120°，360°．点评：本题主要考查了测量角的能力．12.如图中∠1=65°求∠2、∠3和∠4的度数，计算这4个角的总和是多少．∠2=∠3=∠4=∠1+∠2+∠3+∠4=．【答案】115°，65°，115°，360°【解析】根据平角的定义可求∠2、∠3和∠4的度数，再将∠1、∠2、∠3、∠4的度数相加即可求解．解：∠2=180﹣65°=115°，∠3=180﹣115°=65°，∠4=180﹣65°=115°，∠1+∠2+∠3+∠4=65°+115°+65°+115°=360°．故答案为：115°，65°，115°，360°．点评：解题的关键是熟悉平角的度数等于180°的性质．13.看图填空．已知：∠1=48°∠2=﹙﹚∠3=﹙﹚∠4=﹙﹚【答案】132°；48°；132°【解析】（1）∠1与∠2的和是180°，则∠2=180°﹣∠1；（2）∠2与∠3的和是180°，则∠3=180°﹣∠2；（3）∠1与∠4的和是180°，则∠4=180°﹣∠1．解：（1）∠2=180°﹣∠1，=180°﹣48°，=132°；（2）∠3=180°﹣∠2，=180°﹣132°，=48°；（3）∠4=180°﹣∠1，=180°﹣48°，=132°．故答案为：132°；48°；132°．点评：本题主要考查角的度量，用平角为180°这一知识点解决问题．14.如图中∠1=40°，你能求出∠2、∠3、∠4其他几个角的度数吗？【答案】∠2=140°，∠3=40°，∠4=140°【解析】根据平角的定义依次可求∠2、∠3、∠4的度数．解：∠2=∠4=180°﹣∠1=180°﹣40°=140°，∠3=180°﹣∠2=180°﹣140°=40°．答：∠2=140°，∠3=40°，∠4=140°．点评：考查了角的度量，关键是熟悉平角等于180°的知识点．15.量出图中角的度数．∠2=．【答案】【解析】用量角器的圆点和角的顶点重合，0刻度线和角的一条边重合，另一条边在量角器上的刻度就是该角的度数．据此解答．解：测量结果如下图：点评：本题考查了学生测量角的能力，要注意两个重合．16.求图中出∠2的度数．∠2=．【答案】15°【解析】观察图形可知，∠2与75°组成一个直角，据此计算即可解答．解：∠2=90°﹣75°=15°．故答案为：15°．点评：解答此题的关键是利用图形中特殊角即直角的度数进行计算解答．17.如图一张长方形纸，把它的一角折叠过来，已知∠1=30°你能求出∠2等于多少度吗？【答案】∠2=30°【解析】根据折叠的方法可得：∠1=∠3=30°，因为∠1、∠2、∠3的和是90°，所以∠2=90°﹣30°﹣30°=30°．解：根据题干分析可得：∠2=90°﹣30°﹣30°=30°．答：∠2=30°．点评：抓住图中的特殊角，即90度的角，根据折叠的方法得出图中∠1=∠3，即可解答问题．18.量出下列各角的度数．【答案】【解析】用量角器的圆点和角的顶点重合，0刻度线和其中一条边重合，另一条边指向的刻度，就是这个角的度数．解：测量结果如下：点评：本题考查了学生运用量角器测量角的度数的能力．19.如图，已知∠1=38°，求∠2、∠5各是多少度？（1）∠2=（2）∠5=【答案】（1）142°；（2）52°【解析】（1）由题意得出∠1和∠2组成一个平角，所以∠2=180°﹣∠1；（2）∠5与∠1的对顶角组成一个直角，所以∠5=90°﹣∠1的对顶角的度数，又因为对顶角度数相等，所以∠1的对顶角和∠1的度数相等；．代数计算即可．解：（1）∠2=180°﹣∠1=180°﹣38°=142°；（2）∠5=90°﹣38°=52°．故答案为：（1）142°；（2）52°．点评：解决本题的关键是根据各个角之间的关系解答．20.计算各角的度数，并指出是什么角．∠1=50度，是角．∠2=，是角．∠3=，是角．∠4=，是角．【答案】锐；130°，钝；50°，锐；130°，钝【解析】（1）∠1=50度，小于90度，是锐角；（2）∠2和∠1组成平角，所以∠2=180°﹣∠1=180°﹣50°=130°，大于90度而小于180度，是钝角；（3）∠3和∠1是对顶角，度数相等，是锐角；（4）∠4和∠2是对顶角，度数相等，是钝角；据此解答即可．解：由分析得出：∠1=50度，是锐角．∠2=180°﹣∠1=180°﹣50°=130°，是钝角．∠3=50°，是锐角．∠4=130°，是钝角．故答案为：锐；130°，钝；50°，锐；130°，钝．点评：解决本题的关键是根据角之间的关系计算出角的度数，再根据角的分类标准判断角的类别．21.钟面上12时15分时，分针和时针组成了直角．．【答案】错误【解析】钟面上12时15分，时针从12走的格子数是15÷（60÷5），分针从12走的格子数是15个，时针和分针之间的格子是[15﹣15÷（60÷5）]个，在钟面上每个格子对应的圆心角是360°÷60，据此解答．解：时针从12走的格子数是：15÷（60÷5），=15÷12=1.25（个），分针从12走的格子数是15个，时针和分针之间的格子是：15﹣1.25=13.75（个），钟面上12点15分，时针和分针所成的角度是：360°÷60×13.75，=6°×13.75，=82.5°；直角是90度．所以钟面上12时15分时，分针和时针组成的角不是直角．故答案为：错误．点评：本题的关键是算出时针和分针之间的格子数，再根据每个格子对应的圆心角求出其度数．22.计算出如图中∠1=度，∠2=度．【答案】30，60【解析】根据平角和直角的定义可求∠1的度数，再根据直角三角形两个锐角的和为90°可求∠2的度数．解：∠1=180°﹣60°﹣90°=30°，∠2=90°﹣30°=60°．故答案为：30，60．点评：考查了平角和直角的定义和直角三角形的性质．23.已知∠1=28°，∠2=．【答案】62°．【解析】观察图形可知，∠1与∠2组成了一个直角，据此可得∠2就等于90°∠1的度数，据此即可解答．解：90°﹣28°=62°，答：∠2=62°，故答案为：62°．点评：解答此类问题的关键是利用图形中特殊角的度数进行计算解答．24.求出下面各角的度数．已知：∠1=150°∠2=；∠3=；∠4=．【答案】30°；150°；30°【解析】观察图形可知，∠1与∠2组成了一个平角，所以∠1+∠2=180°，由此即可得出∠2=180°﹣150°=30°，同样的道理可以求出∠3和∠4的度数．解：根据题干分析可得：∠2=180°﹣150°=30°；∠3=180°﹣30°=150°；∠4=180°﹣150°=30°；故答案为：30°；150°；30°．点评：解答此题的关键是利用图形中特殊角的度数，如直角或平角，利用它们的度数进行计算即可解答．25.已知∠1=28°求∠2、∠3、∠4和∠5各是多少度？【答案】∠2=152°，∠3=28°，∠4=90°，∠5=62°【解析】先找到特殊的角∠4=90°，则可得：∠1+∠5=90°，所以∠5=90°﹣∠1=90°﹣28°=62°；又因为∠1+∠2=180°，所以∠2=180°﹣∠1=180°﹣28°=152°；因为∠2+∠3=180°，所以∠3=180°﹣∠2=180°﹣152°=28°；据此解答．解：∠4=90°，∠5=90°﹣∠1=90°﹣28°=62°，∠2=180°﹣∠1=180°﹣28°=152°，∠3=180°﹣∠2=180°﹣152°=28°；答：∠2=152°，∠3=28°，∠4=90°，∠5=62°．点评：本题考查根据相交的线组成的角来求未知的角，关键是利用平角等于180°和直角等于90°这个知识点解答．26.已知∠1=130°，∠2=，∠3=，∠4=．【答案】50°，130°，50°【解析】因∠1和∠2在同一条直线上，它们组成了一个平角，∠2和∠3在同一条直线上，它们组成了一个平角，∠1和∠4在同一条直线上，它们组成了一个平角．据此解答．解：（1）∠2=180°﹣∠1，∠2=180°﹣130°，∠2=50°；（2）∠3=180°﹣∠2，∠3=180°﹣50°，∠3=130°；（3））∠4=180°﹣∠1，∠4=180°﹣130°，∠4=50°；故答案为：50°，130°，50°．点评：本题主要考查了学生根据角的位置关系求角的度数的能力．27.计算图形中角的度数．∠1=55°，∠2=，∠3=，∠4=．【答案】125°；55°；125°【解析】两条直线相交，组成的四个角中，相邻的两个角互补，对顶角相等，据此即可解答．解：观察图形可知，∠2=∠4=180°﹣55°=125°（邻补角的定义），∠3=∠1=55°（等对角相等），故答案为：125°；55°；125°．点评：此题主要考查两条直线相交组成的四个角之间的关系的灵活应用．28.用量角器量出下面各角的度数．【答案】【解析】先把量角器放在角的上面，使量角器的中心和角的顶点重合，零度刻度线和角的一条边重合，角的另一条边所对的量角器上的刻度，就是这个角的度数．解：根据角的度量方法量出这两个角的度数分别是130°、55°、55°、70°．在图上标出如图：点评：此题主要是考查根据角的度量方法正确量出各角度数．29.（1）把下面的梯形分割成一个平行四边形和一个三角形．（2）下面∠1的大小是度．【答案】（2）70．【解析】（1）将三角板的一条直角边和直尺的上边缘都与梯形的一个腰重合，然后平移直尺，当直尺的上边缘正好与梯形上底的另一个端点重合时，过这个端点沿直尺上边缘画线段，与梯形的下底交于一点，此线段即为平行于梯形腰的线段，从而可以得到符合要求的平行四边形和三角形．（2）用量角器测量出角的度数即可．解：如图所示：；（1）红色线段即为所求；（2）∠1的大小为70度．故答案为：（2）70．点评：此题主要考查：过直线外一点作已知直线的平行线的方法．30.测量出各角的度数．测量的结果：∠1=；∠2=；∠3=．【答案】40°，60°，80°【解析】先把量角器放在角的上面，使量角器的中心和角的顶点重合，零度刻度线和角的一条边重合，角的另一条边所对的量角器上的刻度，就是这个角的度数．解：如图所示：，∠1=40°，∠2=60°，∠3=80°．故答案为：40°，60°，80°．点评：此题主要是考查根据角的度量方法正确量出各角度数．31.已知∠1=60°，求∠2、∠3和∠4的度数．【答案】∠2=30°，∠3=60°，∠4=30°【解析】根据∠3+∠4=90°，可知∠1+∠2=60°，那么就可以求出∠2=90°﹣∠1=90°﹣60°=30°；又因为∠2+∠3=90°，∠3+∠4=90°，同理可以求出∠3和∠4的度数，据此解答．解：∠2=90°﹣∠1=90°﹣60°=30°，∠3=90°﹣∠2=90°﹣30°=60°，∠4=90°﹣∠3=90°﹣60°=30°；答：∠2=30°，∠3=60°，∠4=30°．点评：本题关键是理解相邻的两个角成直角．32.如图：∠1=48°；∠2=．【答案】42°【解析】观察图形可知，∠1与∠2组成一个直角，所以∠2等于90度减去∠1的度数．解：∠2=90°﹣48°=42°，故答案为：42°．点评：抓住图形中的特殊角的度数，即可计算解答．33.算一算：∠1=；∠2=；∠3=．【答案】145°；90°；55°【解析】根据平角的定义即可求出∠1，∠2，∠3的度数．解：∠1=180°﹣35°=145°；∠2=180°﹣90°=90°；∠3=180°﹣125°=55°．故答案为：145°；90°；55°．点评：解题的关键是熟悉平角等于180°的定义．34.根据图中的信息解答下列问题：（1）车站到学校的路线与游乐园到学校的路线的夹角的度数是．（2）电影院位置在车站的方向，在游乐园的方向．（3）量一量学校到电影院的图上距离是多少厘米？根据图上比例尺，求出学校到电影院的实际距离是多少？【答案】125°，东偏南20°，北偏西40°【解析】（1）用量角器的圆点和角的顶点重合，0刻度线和角的一条边重合，另一条边在量角器上的刻度就是该角的度数．（2）根据图例，量出角度，在生活中一般我们先说与物体所在方向离的较近（夹角较小）方位．（3）量得学校到电影院的图上距离是2厘米，根据图上距离÷实际距离=比例尺，求出实际距离，据此解答．解：（1）量得车站到车站到学校的路线与游乐园到学校的路线的夹角的度数是125°，（2）测量如下图：（3）2÷=50000（厘米）=500米．答：学校到电影院的实际距离是500米．故答案为：125°，东偏南20°，北偏西40°．点评：本题的难点是画图求出电影院在车站和游乐园的方向，以及根据比例尺求实际距离．35.用水彩笔在下图中按要求描一个角．【答案】【解析】通过观察可知，图中把平角进行了四等分，所以每个小角是45°，三个小角就是135°，由此描出即可．解：根据要求描出如下：点评：此题考查了学生的观察能力和动手操作能力．36.（2012•仙游县模拟）如图是一张长方形纸折起来以后的图形，已知∠1=30°，那么∠2=度．【答案】75【解析】如图，把这张长方形纸展开，以∠1的顶点为顶点的角是一个平角，平角=180°，折起来后∠2盖住了一个与它度数相等的角，也就是2∠2与∠1的和是180°，据此解答．解：由分析得：∠2=（180°﹣30°）÷2=150°÷2=75°；故答案为：75．点评：本题是考查简单的图形折叠问题、角的度量．37.如图所示的角是度，以A点为顶点，再在这个角内画一个60度的角．【答案】160【解析】（1）用量角器的圆点和角的顶点A重合，0刻度线和角的一条边重合，另一条边在量角器上的刻度就是该角的度数．（2）用量角器的圆点和角的顶点A重合，0刻度线和角的一边重合，在量角器60°的刻度上点上点（点在角的内部），过角的顶点和刚作的点，画射线即可．解：（1）量得角的度数是160度，（2）画图如下：故答案为：160．点评：本题考查了学生测量角和画角的能力．38.操作题一：（1）量出所需数据算出面积和周长．（2）在右图圆上取一点，C连接AC、CB，量出∠C=°，像这样再画几个角，量一量这些角的度数你发现．【答案】90，它们的度数都等于90°【解析】（1）先测量出AB的长，再根据半圆的面积公式：S=πr2，半圆的周长公式：C=πd+d计算即可；（2）测量角的度数时：第一步：点重合，量角器的中心点与顶点重合．第二步：线重合，量角器的零刻度线与角的一边重合．第三步：读度数，看角的另一边落到量角器的哪个刻度线上，这个刻度数是这个角的度数．根据量出这些角的度数即可发现规律．解：（1）测量可得AB=3.4厘米．面积为：×3.14×（3.4÷2）2，=×3.14×1.72，=4.5373（平方厘米）；周长为：×3.14×3.4+3.4，=5.338+3.4，=8.738（厘米）．答：面积是4.5373平方厘米，周长是8.738厘米．（2）如图所示：测量可得∠C=90°，像这样再画几个角，量一量这些角的度数我发现：它们的度数都等于90°．故答案为：90，它们的度数都等于90°．点评：考查了长度的测量，角的度量，半圆的面积和周长计算，注意直径所对的圆心角等于90°．39.写出下面各角的度数：∠1=；∠2=；∠3=．【答案】43°；60°；30°【解析】（1）因为三角形的第三个角与68°角组成一个平角，所以第三个角=180°﹣68°，又因为三角形三个内角和是180度，即∠1、25°和第三个角的和是180度，即可求出∠1；（2）∠2和直角、30°角组成一个平角，所以∠2=180°﹣90°﹣30°；又因为∠2和∠3组成一个直角，所以∠3=90°﹣∠2，代数计算即可．解：（1）∠1=180°﹣（180°﹣68°）﹣25°=43°；（2）∠2=180°﹣90°﹣30°=60°；∠3=90°﹣∠2=90°﹣60°=30°．故答案为：43°；60°；30°．点评：解决本题的关键是根据图意找出相关角度之间的关系．40.一个60°的角用放大镜看，角变大了．．【答案】错误【解析】角的大小与两边的长短无关，只与角两边张开的大小有关，所以用一个放大镜看一个60度的角，仍然是60度．解：用一个放大镜看一个60°的角，从放大镜中看到的角是60°；所以原题说法错误．故答案为：错误．点评：此题主要考查角的意义，应理解放大镜放大的只是角两边的长短．。

角的比较和运算◆随堂检测1、如图，∠AOC和∠BOD都是直角，如果∠AOB=1400，则∠DOC的度数是（）A、300B、400C、500D、6002、一副三角尺可拼成很多角，如下图是由一副三角尺拼成的2个图形，请你计算：在第一个图中：∠ACD= °，∠ABD= °；在第二个图中：∠BAG= °，∠AGC= °。

图1 图23、将一副直角三角板(如图)叠在一起，使直角顶点重合于点O，则∠AOB+∠DOC= 。

4、计算：102°43′32″+77°16′28″＝____________；87 o2′36″—36o37′24″＝______________。

5、如图，已知∠AOB=50º，OD平分∠BOC，OE平分∠AOC。

求∠EOD的度数。

_1 _ D_ C_ B_ A_ O6.如图，（1）已知∠AOB 是直角，∠BOC=30°，OM 平分∠AOC ，ON 平分∠BOC ，求∠MON 的度数。

（2）如果（1）中∠AOB=α，其他条件不变，求∠MON 的度数。

（3）你从（1）、（2）的结果中能发现什么规律？ 课后检测1、平面内两个角∠AOB=60°，∠AOC=20°，OA 为两角的公共边，则∠BOC 为（ ） A 、40° B、80° C、40°或80° D、无法确定2、下面一些角中，可以只用一副三角尺（不用量角器）画出来的角是（ ） （1）150的角 （2）650的角 （3）750的角 （4）1350的角 （5）1450的角 A 、（1）（3）（4） B 、（1）（3）（5） C 、（1）（2）（4） D 、（2）（4）（5） 3、已知：∠A=50º24’，∠B=50.24º，∠C =50º14’24”，那么下列各式正确的是（ ） A 、∠A>∠B>∠C B 、∠A>∠B=∠C C 、∠B>∠C>∠A D 、∠B=∠C>∠A4.在∠AOB 的内部取一点，作射线OC,则一定存在（ ） A.∠AOB>∠AOC B ∠AOC>∠BOC C ∠BOC>∠AOC D ∠AOC ＝∠BOC5.如图：∠AOB ＝∠COD ＝90°，∠AOC=∠1，则∠BOD 的度数是（ ） A. 90°+∠1 B. 90°+2∠1 C. 180°-∠1 D. 180°-2∠1_ O_ D_ C_ B_ A_ F_ E_ C_ B_ A_ E _ D_ B_ A6. .如图已知∠AOB=90°,∠BOC=60°, OD 是∠AOC 的平分线，求 ∠BOD 的度数。

小学数学四年级角的度量知识点总结梳理汇总附练习题文章目录四年级数学角的度量知识点整理一、本节学习指导本节学习角的相关知识，同学们可以先回忆一下直线、斜线相关知识。

本节中我们要掌握角的表示、量角器的使用。

本节有配套免费学习视频。

二、知识要点1、直线、射线、角直线：向两端无限延伸的线，直线无端点。

射线：能像一个方向延伸的线，射线有一个端点。

线段：不能延伸的线，线段有两个端点。

角：具有公共端点的两条射线组成的图形叫做角。

这个公共端点叫做角的顶点，这两条射线叫做角的两条边。

（1）、直线和射线都可以无限延伸，因此无法量出长短。

（2）、线段可以量出长度。

（3）、线段有两个端点，直线没有端点，射线只有一个端点。

3、角的特征角有一个顶点，两条边，如下图角通常用符号“∠”来表示上图中的两个角表示为：∠1 ，∠2；读作：角 1 ，角24、角的大小比较：角的计量单位是“度”，符号“°”，把半圆平分成180等份，每一份所对的角的大小是l 度。

记做1°。

角大小的测量借助量角器，如下图。

测量方法：量角注意两对齐：量角器的中心和角的顶点对齐；量角器的0刻度线和角的一条边对齐。

做到两对齐后看角的另一条边对着刻度线几，这个角就是几度。

看刻度要分清内外圈。

这里我教大家一个小窍门：分清内外圈，紧跟0刻度；0刻度在外圈就看外圈的刻度。

0刻度在内圈就看内圈的刻度。

牢牢记住不忘记。

注意：角的大小与角的两边画出的长短没关系。

角的大小要看两条边叉开的大小，叉开得越大，角越大。

5、角的分类：锐角＜90°，直角=90°，90°＜钝角＜180°，平角=180°=2个直角，周角=360°=2个平角=4个平角6、画角步骤：以画65°的角为例（1）画一条射线，使量角器的中心和封线的端点重合，0 刻度线和射线重合。

（2）在量角器65°刻度线的地方点一个点。

（3）以画出的射线的端点为端点，通过刚画的点，再画一条射线。

角的度量练习题一、填空1.从一点引出两条( )所组成的图形叫做角，这个点叫做角的( )，这两条射线叫做角的( )。

2.计量角的大小的单位是( )。

3.在一个直角三角形中，有两个相等的角，那么这两个角都是( )。

4.用一副三角尺中( )度和( )度的角可以拼成105度的角。

二、精心挑选1.度量一个角，角的一条边对着量角器上内圈“0”的刻度，另一条边对着内圈刻度“60”，这个角是( )。

A.60度B.180度C.20度2.一个5倍的放大镜看一个15度的角，这个角是( )。

A.15度B.20度C.75度3.度量一个角，角的一条边对着量角器上内圈“180”的刻度，另一条边对着内圈刻度“60”，这个角是( )。

A.60度B.120度C.无法确定三、量一量1.量出下面各角的度数。

( )度( )度( )度( )度( )度( )度2.量出下面各图中角的度数。

三个角的度数和是( ) 三个角的度数和是( )四个角的度数和是( ) 四个角的度数和是( )1．下图中④是直线，①是射线，②是线段．⑦是锐角，⑧是平角，⑨是周角，⑥是钝角．2．从一点引出两条射线，所组成的图形叫作角．这两条射线叫作角的边，角通常用符号∠来表示．．量角时，量角器的中心与重合，零刻度与重合，角的另一条边所对的量角器上的刻度，就是这个角的．重合，零刻度与重合，角的另一条边所对的量角器上的刻度，就是这个角的11．看图计算．12．①如图∠1=50°，求∠2、∠3、∠4的度数．13．14．②已知，图中∠1=30°，∠3=90°，求∠2、∠4、∠5、∠6各是多少度？15．16．③已知图中∠1=30°，∠3=40°，求∠2、∠4、∠5各是多少度？17．18．下图是一个大型花池中小路的平面图，你能否不重复地一次走完所有的小路？进口、出口应分别设在什么地方？19．一、填空题（每空1分，共20分）1、角是从一点引出的两条( )所组成的图形,这一点是角的（）,两条射线是角的( )。

角的度量练习题角的度量练习题练习就是用题进行多角度、多层次的训练，通过多方面的强化，恰当的重复来掌握知识和技巧。

下面小编为大家带来角的度量练习题，希望大家喜欢！角的度量练习题1一、我会填。

(1)直线上两点之间的一段叫( )，它有( )个端点。

把线段的一端无限延长就得到一条( )，如果把线段的两端无限延长就得到一条( )。

射线有( )个端点，它可以向一端无限延长。

直线有( )个端点，它可以向两端无限延长。

(2)在两点之间可以画出很多条线，其中( )最短。

过一点可以画( )条直线。

当两条直线相交成直角时，这两条直线( )，这两条直线的交点叫做( )。

(3)从一点引出两条( )所组成的图形叫做角，这一点叫做角的( )，这两条射线叫做角的( )。

( )的角叫做锐角，直角等于( )°，大于( )°而小于( )°的角叫做钝角。

(4)量角时，角的顶点要与量角器的( )对齐，角的一边要与量角器的( )重合，而角的另一边所对量角器的度数就是这个角的大小。

角的大小要看两边叉开的大小，叉开得( )，( )就越大。

角的大小与画出的边的长短( )。

(5)钟面上的时针和分针2时成( )角，3时成( )角，6时成( )角。

(6)我们学过的角有( )角、( )角、( )角、( )角、( )角。

1平角=( )度=( )直角1周角=( )度=( )平角=( )直角(7)∠1与∠2的和是184°，∠2=54°，那么∠1=( )。

∠1+∠2+∠3=180°，其中∠1=52°，∠2=46°，那么∠3=( )。

∠1是∠2的3倍，∠1=120°，∠2=( )。

二、判断，请在括号里对的画“√”，错的画“×”。

1.线段是直线上两点之间的部分。

( )2.过一点只能画出一条直线。

( )3.一条射线长6厘米。

( )4.手电筒射出的光线可以被看成是线段。

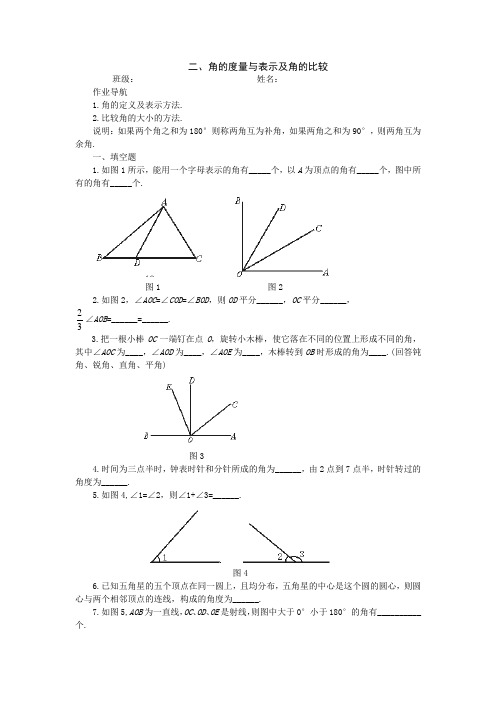
二、角的度量与表示及角的比较班级：___________________________姓名：___________________________ 作业导航1.角的定义及表示方法.2.比较角的大小的方法.说明：如果两个角之和为180°则称两角互为补角，如果两角之和为90°，则两角互为余角.一、填空题1.如图1所示，能用一个字母表示的角有_____个，以A 为顶点的角有_____个，图中所有的角有_____个.图1 图22.如图2，∠AOC =∠COD =∠BOD ，则OD 平分______，OC 平分______，32∠AOB =______=______. 3.把一根小棒OC 一端钉在点O ，旋转小木棒，使它落在不同的位置上形成不同的角，其中∠AOC 为____，∠AOD 为____，∠AOE 为____，木棒转到OB 时形成的角为____.(回答钝角、锐角、直角、平角)图34.时间为三点半时，钟表时针和分针所成的角为______，由2点到7点半，时针转过的角度为______.5.如图4,∠1=∠2，则∠1+∠3=______.图46.已知五角星的五个顶点在同一圆上，且均分布，五角星的中心是这个圆的圆心，则圆心与两个相邻顶点的连线，构成的角度为______.7.如图5,AOB 为一直线，OC 、OD 、OE 是射线，则图中大于0°小于180°的角有__________个.图58.如果一个角的度数为n ，则它的补角为______，余角为______.9.∠α的补角为125°，∠β的余角为37°，则α、β的大小关系为α__________β. 二、选择题10.一个角等于它的补角的5倍，那么这个角的补角的余角是（ ） ° ° ° ° 11.两个锐角的和（ ）A.一定是锐角B.一定是钝角C.一定是直角D.以上三种情况都有可能 12.互为补角的两个角度比是3∶2，这两个角是（ ） °,72° °，85° °，80° °，70° 13.下列各角中是钝角的为（ ）A.41周角 B.65平角 C.32直角D.31直角 14.如果角α和角β互为余角,角α与角γ互为补角,角β和角γ的和等于周角的31，那么此三个角分别为（ ）°,15°,105° °,30°, 120° °, 30°,130° °, 20°, 110° 15.如图6，图形表示的是（ ）A.直线B.射线C.平角D.周角图616.船的航向从正北按顺时针方向转到东南方向，它转了（ ） ° ° ° °17.有两个角，它们的比为7∶3，它们的差为72°，则这两个角的关系是（ ） A.互为余角 B.互为补角C.相等D.以上答案都不对 三、解答题18.四个角的和是180°，其中有三个角相等，且都是第四个角的32，求这四个角. 19.如图7，已知∠AOC =∠BOD =75°，∠BOC =30°，求∠AO D.图7 图820.如图8，已知O是直线AB上的点，OD是∠AOC的平分线，OE是∠COB的平分线，求∠DOE的度数.二、角的度量与表示及角的比较一、1. 2 3 72.∠BOC∠AOD∠AOD∠BOC3.锐角直角钝角平角° 165°°°°－n 90°－n 9.＞二、三、°，40°，40°，60°°°。

初一数学角与角的度量试题1.下列各图中表示角的是（）【答案】D【解析】本题主要考查的是角的定义根据角的定义：有公共端点的两条射线组成的图形叫做角，依次分析各项即可。

根据角的定义：有公共端点的两条射线组成的图形叫做角，可知只有D选项中的图表示角，故选D.思路拓展：有公共端点的两条射线组成的图形叫做角，注意不要忽略“公共端点”．2.钟面上时针1小时转______度，分针每分钟转_______度。

【答案】30，6【解析】本题考查的是钟表表盘与角度相关的特征钟表表盘被分成12大格，每一大格所对角的度数为30°，每一大格又被分为5小格，故表盘共被分成60小格，每一小格所对角的度数为6°，根据时针1小时转一大格，分针每分钟转一小格即可得到结果。

钟面上时针1小时转30度，分针每分钟转6度。

思路拓展：钟表表盘被分成12大格，每一大格又被分为5小格，故表盘共被分成60小格，每一小格所对角的度数为6°．分针转动一圈，时间为60分钟，则时针转1大格，即时针转动30°，逆过来同理．3.14400"等于多少分？等于多少度？【答案】240¹，4º【解析】本题考查的是度、分、秒的转化运算进行度、分、秒的转化运算，注意以60为进制．先将秒的部分除以60化为分，再将分的部分除以60化为度．根据1°=60′，1′=60″得，14400"÷60=240′，240′÷60=4°，所以14400"等于240¹，等于4º.思路拓展：由度化分应乘以60，由分化度应除以60，注意度、分、秒都是60进制的，由小单位化大单位要除以60，由大单位化小单位要乘以60.4.下列语句正确的是（）A．两条直线相交组成的图形叫角；B．一条直线可以看成一个平角；C．一个平角的两边可以看成一条直线；D．周角就是一条射线【答案】C【解析】此题考查了角的定义根据角的组成、平角、周角的定义解答，只要举出一个反例即可证明命题错误．A、有公共端点的两条射线组成的图形叫做角，故本选项错误；B、直线和平角是两个概念，平角是由处在同一直线上方向相反的两条射线构成的角，不能将直线和射线混为一谈，故本选项错误；C、平角等于180 º，故一个平角的两边可以看成一条直线，本选项正确；D、有公共端点的两条射线组成的图形叫做角，周角等于360 º，周角的两边重合，故本选项错误；思路拓展：解答此题，必须明确角的边、顶点、平角与直线的区别与联系，侧重于对基本概念的理解．5.下列四个图形中，能同时用∠1，∠ABC，∠B三种方法表示同一个角的图形是（）【答案】B【解析】本题考查的是角的表示方法根据角的表示方法进行逐一分析，即角可以用一个大写字母表示，也可以用三个大写字母表示．其中顶点字母要写在中间，唯有在顶点处只有一个角的情况，才可用顶点处的一个字母来记这个角，否则分不清这个字母究竟表示哪个角．角还可以用一个希腊字母（如∠α，∠β，∠γ、…）表示，或用阿拉伯数字（∠1，∠2…）表示．A、因为顶点B处有四个角，所以这四个角均不能用∠B表示，故本选项错误；B、因为顶点B处只有一个角，所以这个角能用∠1，∠ABC，∠B表示，故本选项正确；C、因为顶点B处有三个角，所以这三个角均不能用∠B表示，故本选项错误；D、因为顶点B处有三个角，所以这三个角均不能用∠B表示，故本选项错误．故选B．思路拓展：角的表示方法一般有以下几种：①一个大写字母，②一个希腊字母，③一个阿拉伯数字，④三个大写字母且表示顶点的字母写在中间．要注意，当顶点处有多个角时，不能用一个大写字母表示，以免混淆．6.下列关于角的描述正确的是：（）A．角的边是两条线段；B．角是由两条射线组成的图形C．角可以看成一条射线绕着它的端点旋转而成图形；D．角的大小与边的长短有关【答案】C【解析】本题主要考查的是角的定义根据角的定义：有公共端点的两条射线组成的图形叫做角，角的大小与边的长短无关，只与两边张开的程度有关，依次分析各项即可。

角的比较与运算【专项训练】2008年12月制卷人:王家和一、判断题：1、小于平角的角叫做钝角。

( )2、两条射线组成的图形叫做角。

( )3、平分一个角的射线叫做角的平分线。

( )4、因为钝角必然大于直角，所以大于直角的角都是钝角。

( )5、互补的两个角一定有一个是钝角，另一个是锐角。

( )6、如果两个角都是钝角，那么这两个角相等。

( )7、锐角和钝角之和是平角。

( )8、互余的两个角一定都是锐角。

( )9、如果∠1`+∠2=180︒，∠2+∠3=180︒，则∠1=∠3 ( )二、填空题：1、57.32︒= 度分秒，17︒14'24''= 度。

2、如图∠AOC=+∠BOC=∠BOD－∠=∠AOC－∠3、如图，直线AMB，∠AMC=52︒48'，∠BMD=74︒30'，则∠CMD=。

4、一个角的余角为721842︒'''，则这个角的补角为。

5、已知∠AOB是直角，OM平分∠BOC，ON平分∠AOC，那么∠MON=。

6、已知∠1=2∠2，∠1的余角的3倍等于∠2的补角，则∠1= ，∠2= 。

7、已知如图：∠1∶∠2∶∠3∶∠4=1∶2∶3∶4，则∠2+∠3=，∠1与∠4互为角。

8、已知如图：直线AB和CD相交于点O，若∠AOD=5∠AOC，则∠BOC=。

三、选择题：1、在∠AOB的内部任取一点C，作射线OC那么有：( )A．∠AOC=∠BOC B．∠AOC >∠BOCC．∠BOC >∠AOB D．∠AOB >∠AOC2、如图，由A测B，方向是：( )A．南偏东32︒B．南偏东58︒C．北偏西32︒D．北偏西58︒3、如图：OC是∠AOB的平分线，OD是∠BOC的平分线，那么下列各式中正确的是：( )ABCD．．．．∠=∠∠=∠∠=∠∠=∠COD AOCAOD AOBBOD AOBBOC AOB122313324、如图，O是直线AB上一点，∠BOD=90︒，∠COE=90︒，那么下列各式中错误的是：( )A．∠AOC=∠DOEB．∠COD=∠BOEC．∠AOD=∠BODD．∠BOE=∠AOC5、下列各式中，正确的是：( ) A ．8358350.︒=︒'B ． 3712363748︒'''=︒.C ． 2424242444︒'''=︒.D ． 41254115.︒=︒'6、角α的余角的补角是：( ) A ．180︒-αB ．90︒+αC ．90︒-αD ．180︒+α7、两个锐角的和：( ) A ．一定是锐角 B ．一定是直角C ．一定是钝角D ．可能是锐角、直角、钝角8、如图，下列说法中正确的是：( ) A ．OA 的方向是北偏东30︒ B ．OB 的方向是北偏西25︒ C ．OC 的方向是东偏西45︒ D ．OD 的方向是西北方向75︒9、下列说法中正确的是：( ) A ．锐角大于它的余角 B ．锐角小于它的补角C ．锐角不小于它的补角D ．锐角的补角小于锐角的余角10、一个锐角和它的余角之比是5∶4，那么这个锐角的补角的度数是：( ) A ．100︒B ．120︒C ．130︒D ．140︒11、已知锐角α，那么α的补角与α的余角的差是：( ) A ．60︒+αB ．90︒C ．120︒D ．180︒-α四、已知下列条件，求角α的度数。

角的度量试题一、选择题1. 两个角的度数之和是90°，则它们是（）。

A. 直角B. 钝角C. 锐角D. 平角2. 两个角的度数之和是180°，则它们是（）。

A. 平角B. 钝角C. 锐角D. 对顶角3. 三个角的度数之和是180°，则它们是（）。

A. 平角B. 钝角C. 对顶角D. 锐角4. 直角的度数是（）。

A. 90°B. 180°C. 270°D. 360°5. 钝角的度数大于（）。

A. 90°B. 180°C. 270°D. 360°二、判断题判断下列说法是否正确，正确的用“√”表示，错误的用“×”表示。

1. 两个补角的度数之和是180°（）。

2. 两个互补角的度数之和是90°（）。

3. 对顶角的度数相等（）。

4. 钝角的度数始终大于90°（）。

5. 平角的度数是360°（）。

三、计算题1. 一个角的度数是130°，它的补角度数是多少？2. 一个角的度数是75°，它的互补角度数是多少？3. 两个角的度数之和是120°，它们是对顶角还是相邻角？4. 两个角的度数之和是120°，它们的补角分别是多少？5. 三个角的度数依次是x°、2x°和3x°，它们的度数之和是180°，求x的值。

四、解答题1. 画出一个锐角和一个钝角的示意图。

2. 解释对顶角的概念，并举例说明。

3. 解释相邻角的概念，并举例说明。

4. 解释补角的概念，并举例说明。

5. 证明两个互补角的度数之和是90°。

以上是角的度量试题，希望你在作答时能认真思考并且准确回答。

祝你好运！。

角的度量习题一、填空题。

1.从一点引出两条( )所组成的图形叫做角，这个点叫做角的( )，这两条射线叫做角的( )。

2.角的两边在一条直线上，这样的角叫做( )角，它有( )度，它等于( )个直角。

3.计量角的单位是( )。

4.1周角=( )平角=( )直角=( )45°的角5.时钟在5时的时候，它的时针和分针成( )角。

6.∠1与∠2的和是184°，∠2=54°，那么∠1=( )。

7.∠1+∠2+∠3=180°，其中∠1=52°，∠2=46°，那么∠3=( )。

8.∠1是∠2的3倍，∠1=120°，∠2=( )。

二、判断题。

(1)角的两边越短，角的度数越小。

( )(2)线段比射线短，射线比直线短。

( )(3)平角就是一条直线，周角就是一条射线。

( )(4)时钟在9点整时，时针和分针成直角。

( )(5)两个锐角的和一定比直角大。

( )(6)3点30分时，时针和分针成直角。

( )(7)角的两条边越长，这个角越大。

( )(8)大于90°的角叫做钝角。

( )(9)小于90°的角叫做锐角。

( )(10)一个平角等于90°。

( )三、能力素质提高号称“数学游戏界三剑客”之一的英国人利·欧也斯特·杜德尼(1857～1931)曾经设计了一把13厘米长，但仅有4个刻度的直尺(1、4、5、11厘米)。

别看这把尺只有4个刻度，但它能量出1～13厘米的所有整厘米的长度，你一定感到惊奇吧!那么你能试着利用这把尺量出1～13厘米所有整厘米的长度吗?拓展创新1.用一副三角板拼成下面度数的角。

180° 120° 135° 75° 105° 150°2.钟面上分针旋转720°时，时针旋转了多少度?智能趣题欣赏飞飞把长方纸条ABCD粘成一个环，使A与C重合，B与D重合，就是把一端拧转180°，再与另一端粘合。