最新人教版初中七年级上册数学《角的比较与运算》练习题

角的比较与运算（时间：40分钟，满分68分）班级：___________姓名：___________得分：___________一、选择题（每题3分）1.如图，直线AB、CD相交于点O，OA平分∠EOC，∠EOC=70°，则∠BOD的度数等于（）A.40°B.35°C.30°D.20°【答案】B【解析】试题分析：根据角平分线的性质可得∠AOC=35°，根据对顶角的性质可得∠BOD=∠AOC=35°.考点：角平分线的性质.2．将一副直角三角尺如图放置，若∠AOD=20°，则∠BOC的大小为（）A.140° B．160° C．170° D．150°【答案】B.【解析】试题分析：根据题意可知，；又=90°∠=∠-∠=︒-︒=︒BOC AOB CODCOD COD AOD902070∠=∠+∠+70°=160°.考点：直角三角形的性质.3．如图，∠AOB是直角，∠AOC=38°，OD平分∠BOC，则∠AOD的度数为（）A．52° B．38° C．64° D．26°【答案】C【解析】试题分析：先求得∠BOC的度数，然后由角平分线的定义可求得∠BOD的度数，最后根据∠AOD=∠AOB﹣∠BOD求解即可．解：∠BOC=∠AOB﹣∠AOC=90°﹣38°=52°，∵OD平分∠BOC，∴∠BOD=∠BOC=26°．∴∠AOD=∠AOB﹣∠BOD=90°﹣26°=64°．故选：C ．考点：角平分线的定义．4．如图，已知OC 是∠AOB 内部的一条射线，∠AOC=30°，OE 是∠COB 的平分线．当∠BOE=40°时，∠AOB 的度数是A ．70°B ．80°C ．100°D ．110°【答案】D．【解析】试题分析：OE 是的平分线，COB ∠2,BOC BOE ∴∠=∠AOB BOC AOC∠=∠+∠故选C ．24030110.=⨯+= 考点：角的比较大小．5．（2015秋•常州期末）已知∠AOB=80°，OM 是∠AOB 的平分线，∠BOC=20°，ON 是∠BOC 的平分线，则∠MON 的度数为（ ）A ．30°B ．40°C ．50°D ．30°或50°【答案】D【解析】试题分析：由于OA 与∠BOC 的位置关系不能确定，故应分OA 在∠BOC 内和在∠BOC 外两种情况进行讨论．解：当OA 与∠BOC 的位置关系如图1所示时，∵OM 是∠AOB 的平分线，ON 是∠BOC 的平分线，∠AOB=80°，∠COB=20°，∴∠AOM=∠AOB=×80°=40°，∠BON=∠COB=×20°=10°，∴∠MON=∠BON﹣∠AOM=40°﹣10°=30°；当OA 与∠BOC 的位置关系如图2所示时，∵OM 是∠AOB 的平分线，ON 是∠BOC 的平分线，∠AOB=80°，∠COB=20°，∴∠BOM=∠AOB=×80°=40°，∠BON=∠BOC=×20°=10°，∴∠MON=∠BOM+∠BON=10°+40°=50°．故选：D ．考点：角平分线的定义．6．（2010秋•抚州期末）已知∠MON=30°，∠NOP=15°，则∠MOP=（ ）A ．45°B ．15°C ．45°或15°D ．无法确定【答案】C【解析】试题分析：根据题意先画出图形，再利用角的和差关系分别进行计算即可，注意此题要分两种情况．解：分为两种情况：如图1，当射线OP 在∠MON 内部时，∵∠MON=30°，∠NOP=15°，∴MOP=∠MON﹣∠NOP=30°﹣15°=15°；如图2，当射线OP 在∠MON 外部时，∵∠MON=30°，∠NOP=34°，∴∠MOP=∠MON+∠NOP=30°+15°=45°；故选C．考点：角的计算．7．如图，O 是直线AB 上的一点，OD 平分∠AOC，OE 平分∠BOC，则∠DOE 的度数是 （ ）.αO A ．90180α<<B ．090α<<C ．90α=D ．随OC 位置的变化而变化α【答案】C.【解析】试题分析：因为OD 平分∠AOC，OE 平分∠BOC，所以，，因为12COD AOC ∠=∠12COE BOC ∠=∠，所以=90°，即α的度数为90°.180AOC BOC ∠+∠=︒11802DOE COD COD ∠=∠+∠=⨯︒故选：C.考点：1、角平分线的定义；2、角的计算.8．若∠A = 20°18′，∠B = 20°15′30″，∠C = 20.25°，则（ ）A ．∠A＞∠B＞∠CB ．∠B＞∠A＞∠CC ．∠A＞∠C＞∠BD ．∠C＞∠A＞∠B【答案】A【解析】试题分析：因为∠C = 20.25°= 20°15′，∠A = 20°18′，∠B = 20°15′30″，所以∠A＞∠B＞∠C，故选:A.考点：角的度数换算.9．已知∠AOB=60°,其角平分线为OM,∠BOC=20°，其角平分线为ON ，则∠MON 的大小为A ．20°B ．40°C ．20°或40°D ．10°或30°【答案】C【解析】试题分析：本题需要分两种情况进行讨论，当射线OC 在∠AOB 外部时，∠MON=∠BOM+∠BON=30°+10°=40°；当射线OC 在∠AOB 内部时，∠MON=∠BOM－∠BON=30°－10°=20°．考点：角平分线的性质、角度的计算10．如图，小明将自己用的一副三角板摆成如图形状，如果∠AOB=155°，那么∠COD 等于（ ）A ．15°B ．25°C ．35°D ．45°【答案】B．【解析】试题分析：利用直角和角的组成即角的和差关系计算．解：∵三角板的两个直角都等于90°，所以∠BOD+∠AOC=180°，∵∠BOD+∠AOC=∠AOB+∠COD，∵∠AOB=155°，∴∠COD 等于25°．故选B ．考点：角的计算．11．利用一副三角板上已知度数的角，不能画出的角是（ ）A ．15°B ．135°C ．165°D ．100°【答案】D【解析】试题分析：用三角板画出角，无非是用角度加减法．根据选项一一分析，排除错误答案．解：A 、15°的角，45°﹣30°=15°；B 、135°的角，45°+90°=135°；C 、165°的角，90°+45°+30°=165°；D 、100°的角，无法用三角板中角的度数拼出．故选D ．考点：角的计算．二、填空题（每题3分）12.如图，点A 、O 、B 在一条直线上，且∠BOC=120°，OD 平分∠AOC，则图中∠AOD= °．【答案】30°【解析】试题分析：∵∠AOC+∠BOC=180°，∠BOC=120°，∴∠AOC=180°－120°=60° ∵OD 平分∠AOC ∴∠AOD=∠AOC=×60°=30°．1212考点：角平分线的性质．13．（2015秋•双柏县期末）如图，OC 平分∠AOB，若∠AOC=27°32′，则∠AOB= ．【答案】55°4′．【解析】试题分析：直接利用角平分线的性质得出∠AOC=∠BOC，进而得出答案．解：∵OC 平分∠AOB，∴∠AOC=∠BOC，∵∠AOC=27°32′，∴∠AOB=27°32′×2=54°64′=55°4′．故答案为：55°4′．考点：角平分线的定义；度分秒的换算．14．在同一平面内，已知，，、分别是和的平分线，80AOB ∠=︒20BOC ∠=︒OM ON AOB ∠BOC ∠则的度数是 ．MON ∠【答案】或．50︒30︒【解析】试题分析：分两种情况：射线OC 在∠AOB 的内部和外部，当在内部时，∠MON=∠MOB-∠BON=∠AOB-12∠BOC=（80-20）=30º，当在外部时，∠MON=∠MOB+∠BON=∠AOB+∠BOC=（80+20）=50º，故1212121212∠MON 的度数是50º或30º．考点：角平分线的运用．15．如图，OE 平分∠AOC，OF 平分∠BOC，∠AOE=25°，∠COF=40°，∠AOB＝【答案】130°【解析】试题分析：根据角平分线的性质可得：∠AOC=2∠AOE=50°，∠BOC=2∠COF=80°，则∠AOB=∠AOC+∠BOC=130°.考点：角平分线的性质.16．OC 是∠AOB 内部的一条射线，若∠AOC=21 ，则OC 平分∠AOB；若OC 是∠AOB 的角平分线，则 =2∠AOC．【答案】∠AOB， ∠AOB．【解析】试题分析：∵角平分线定义是：从一个角的顶点出发的一条射线，如果把这个角分成两个相等的角，这条射线就叫这个角的平分线，∴满足OC 平分∠AOB 的条件是：∠AOC=21∠AOB，同理：若OC 是∠AOB 的角平分线，则∠AOB=2∠AOC，故答案为：∠AOB、∠AOB．考点：角平分线的定义．17.如图，∠AOD=80°，∠AOB=30°，OB 是∠AOC 的平分线，则∠AOC 的度数为 度，∠COD 的度数为 度．【答案】60、20．【解析】试题分析：根据角平分线的定义求得∠AOC 的度数，再利用差的关系求∠COD 的度数．解：∵∠AOB=30°，OB 是∠AOC 的平分线，∴∠AOC=2∠AOB=60°，∴∠COD=∠AOD﹣∠AOC=80°﹣60°=20°．故答案为：60、20．考点：角平分线的定义．三解答题18．（8分）如图，已知∠AOC=∠BOD=900，若∠BOC=550，求∠AOB 与∠COD 的度数，并比较这两个角的大小.【答案】∠AOB=∠COD=350【解析】解：∵∠AOC=∠BOD=900∵∠AOC=∠BOC+∠AOB∵∠BOC=550∴∠AOB=350同解：∠BOD=∠BOC+∠COD∴∠COD=350∴∠AOB=∠COD=35019.（9分）如图，O 为直线AB 上一点，，OD 平分，。

新人教七年级数学上册角的比较与运算同步练习一•选择题（共10小题，满分50分，每小题5分）1. （5分）1。

等于（）A. 10'B. 12'C. 60'D. 100'2. （5分）下列关系式正确的是（）A . 35.5°=35°5' B. 35.5 =35°50' C. 35.5°< 35°5' D . 35.5°> 35°5'3. （5分）如果从甲船看乙船，乙船在甲船的北偏东30方向，那么从乙船看甲船，甲船在乙船的（）A .南偏西30°方向B .南偏西60°方向C.南偏东30方向 D .南偏东60°方向4.（5分）已知/ AOB=70。

，以O为端点作射线OC,使/ AOC=42。

，则/ BOC的度数为（）A. 28°B. 112°C. 28 或112°D. 68°5. （5分）如图所示的是一个长方形纸片A BCD沿其上一条线EF折叠后的图形，已知/BEF=105 ° 则/ B'EA 等于（）C__________BD AA. 15°B. 30°C. 45°D. 606. ( 5 分)如图，OB 平分/ AOD , OC 平分/ BOD，/ AOC=45 ° 则/ BOC=(7. （5 分）如图，/ AOB= COE的度数为（）D. 20°/ COD=90 ° OE 平分/ BOD，若/ AOD :/ BOC=5 :1,则/oD. 60°M、N、P、Q四点的位置如图所示，下列结论中，正确的是（o& （5分）已知C .Z PON 比/ MOQ 大D . Z MOQ 与/ MOP 互补10. （ 5 分）若Z a +Z 0=90°, Z 3=Z 9,则Z a 与Z B 的关系是（） A . Z a 与Z B 互余 B . Z a 与Z B 互补 C .Z a 与Z B 相等 D . Z a 大于Z 3二.填空题（共10小题）11. _____________________ 计算 33°52'+21°54'= .12. ____________________________________________ 上午& 30钟表的时针和分针构成角的度数是 ______________________________________________ .13. 如图，OC, OD 是Z AOB 的两条射线，OM 平分Z AOC , ON 平分Z DOB , Z AOB=120 ° Z MON=80 ° 则 Z COD= ____ .15. _____________ 如图，点 O 是直线 AB 上一点，OD 平分Z AOC , OE 平分Z BOC ，若Z COE 等于64° 则Z AOD 等于 度.OE 平分Z AOB ,OF 平分Z BOC .则 Z EOF= ____A ./ NOQ=42 °B .Z NOP=132 9. （ 5分）将一副三角板按如图所示位置摆放，其中Z）16. 如图，0C是/ AOB的角平分线, / COD , / BOD=20 ° 则 / AOD 等于17. 如图，一副直角三角板摆放在一起，射线O M平分/ BOC、ON平分/ AOC，/ MON的度数为18. ____________________________________________________ 已知/ A与/ B互余，若/A=20 °5',则/ B的度数为 ____________________________________ .19. 已知/ a=55°4',则/ a的余角等于 _______ .20. _____________________________________________________________ 一个角的补角的2倍与它的余角的和为240°则这个角的度数为______________________________ 度.三•解答题（共7小题）21. 若一个角的余角的3倍与这个角的补角的和为250 °试求这个角的度数.22•某电视台录制的奔跑吧兄弟第四季”将在周五21: 10播出，此时时钟上的分针与时针所成的角是多少度？在如图中大致标出此时的角（用短箭头、长箭头分别表示时针和分针）并用至少两种方式写出这个角？（可在表盘上标注相应的字母或数字）圍1 图223.如图，是小明家（图中点O）和学校所在地的简单地图，已知OA=2cm , OB=2.5cm , OP=4cm , C为OP的中点.①请用距离和方位角表示图中商场、学校、公园、停车场分别相对小明家的位置；②若学校距离小明家400m，那么商场和停车场分别距离小明家多少米？(1) ________________填空/ BOC=(2) 女口 OD 平分/ BOC , OE 平分/ AOC ，直接写出/ DOE 的度数为 ______ °(3) 试问在(2)的条件下，如果将题目中/ AOC=60。

角的比较与运算一、能力提升1.如图,OC是∠AOB的平分线,OD是∠BOC的平分线,则下列各式正确的是()∠AOCA.∠COD=12∠AOBB.∠AOD=23C.∠BOD=1∠AOB3∠AOBD.∠BOC=322.如图,把长方形ABCD沿EF对折后使两部分重合.若∠1=50°,则∠BFE=()A.70°B.65°C.60°D.50°3.用一副三角尺不可能画出的角度是()A.15°B.75°C.165°D.145°4.已知∠AOB=30°,∠BOC=45°,则∠AOC=()A.15°B.75°C.15°或75°D.不能确定5.如图,将一副三角尺折叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB=.6.如图,已知直线AB,CD相交于点O,OE平分∠COB.若∠EOB=55°,则∠BOD的度数是.7.如图,∠AOC=40°,∠BOD=50°,OM,ON分别是∠AOC,∠BOD的平分线,则∠MON=.8.计算:(1)153°19'42″+26°40'28″;(2)90°3″-57°21'44″;(3)33°15'16″×5.★9.如图,已知OC是∠AOB的平分线.(1)当∠AOB=60°时,求∠AOC的度数;(2)在(1)的条件下,∠EOC=90°,请在图中补全图形,并求∠AOE的度数;(3)当∠AOB=α时,∠EOC=90°,直接写出∠AOE的度数.(用含α的式子表示)★10.如图,∠1∶∠2∶∠3∶∠4=1∶1∶3∶4,求∠1,∠2,∠3,∠4的度数.二、创新应用11.如图1,OM是∠BOC的平分线,ON是∠AOC的平分线,且∠AOB=76°.(1)求∠MON的度数;(2)当OC在∠AOB内另一个位置时,∠MON的值是否发生变化?若不变化,请你在图2中画图加以说明;(3)由(1),(2)你发现了什么规律?当OC在∠AOB外的某一个位置时,你发现的规律还成立吗?请你在图3中画图加以说明.答案一、能力提升1.A 由角平分线的定义可知,∠BOC=∠AOC=12∠AOB ,∠BOD=∠COD=12∠BOC ,所以选项A 中,∠COD=12∠BOC=12∠AOC 正确.2.B 根据折叠后的两个角相等,可知∠BFE=(180°-∠1)÷2=65°.3.D 用三角尺只能画出度数是15的整数倍的角,因为145不是15的整数倍,所以用三角尺不能画出145°的角.4.C 本题没有给出图形,所以∠AOB 和∠BOC 的位置不确定,有两种情况.5.180° 由题图可知,∠AOC+∠DOB=∠AOB+∠COD=90°+90°=180°.6.70° 由OE 平分∠COB ,得∠BOC=2∠EOB=2×55°=110°,所以∠BOD=180°-∠BOC=180°-110°=70°. 7.135° 由角平分线的定义,得∠COM=12∠AOC=12×40°=20°,∠DON=12∠BOD=12×50°=25°, 所以∠MON=180°-∠COM-∠DON=180°-20°-25°=135°. 8.解 (1)153°19'42″+26°40'28″=179°59'70″ =179°60'10″=180°10″.(2)90°3″-57°21'44″=89°59'63″-57°21'44″ =32°38'19″.(3)33°15'16″×5=165°75'80″ =165°76'20″=166°16'20″.9.解 (1)因为OC 是∠AOB 的平分线, 所以∠AOC=12∠AOB.因为∠AOB=60°, 所以∠AOC=30°.(2)如图①,∠AOE=∠EOC+∠AOC=90°+30°=120°;如图②,∠AOE=∠EOC-∠AOC=90°-30°=60°. (3)90°+α2或90°-α2.10.分析 ∠1,∠2,∠3,∠4构成一个周角为360°,再根据题目中∠1∶∠2∶∠3∶∠4=1∶1∶3∶4,因此可以用代数方法解决本题. 解 设∠1=x °,则∠2=x°,∠3=3x°,∠4=4x°.依题意,得x°+x°+3x°+4x°=360°,解得x°=40°.故∠1=40°,∠2=40°,∠3=120°,∠4=160°.二、创新应用11.解(1)∵OM是∠BOC的平分线,ON是∠AOC的平分线,又∠AOB=76°,∴2∠COM+2∠CON=76°,∴∠MON=38°.(2)不发生变化,仍满足2∠COM+2∠CON=76°,∠MON的值不发生变化.(图略)(3)由(1),(2)发现了OC在∠AOB内任一位置时,∠MON的值不发生变化,当OC在∠AOB 外时规律不成立.。

角的比拟与运算一. 填空题1.如图，ZAOB______ ZAOC, ZAOB _______ ZBOC (±1>,=, <)；用量角器度量ZBOC= _____________ , ZAOC____ , ZAOC ______ ZBOC.2.如图，ZAOC= _____________ + _________ ZBOC= ___________3.如图，。

是直线AB上一点，ZBOD=90° , ZCOE=90° ,那么以下各式中错误的选项是（A.ZAOC=ZDOEB. ZCOD=ZBOEC. 2AOD=CBODD. ZBOE= ZAOC4._________________________________________________ 将一副常规三角板拼成如下图的图形，那么______________________________________________________ 度.5.如图，将一副直角三角板叠在一起，使直角顶点重合于点0,贝^iZAOB+ZDOC=度.OC 是从ZAOB 的顶点。

引出的一条射线，假设ZAOB=90° , ZAOB=2ZBOC,求ZAO C 的度数.7.如图.ZAOB=ZCOD,贝lj ( )9. _____________________________________________________________________________ 如图，将一副三角板叠放在一起，使直角的顶点重合于点O,贝IJZAOD+ZCOB 的度数为 _____________ 度.10. 如下图，把一张长方形纸片ABCD 沿EF 折叠，点C 、O 分别落在CD 的位置±, EC 交人。

于点G, 己知/FEC=48° ，那么ZBEG= __________11. 钟面上8： 30这一时刻，钟面上时针与分针所形成的角度是 12.ZAOB=\20° , ZBOC=30° ,那么ZAOC=13. _________________________________________________________ 用三角板画15°角，如下图，使30°角的顶点与45°角的顶点 _______________________________________ , 30°角的相邻直角边与45° 6. A. Z1>Z2 C. Z1<Z2 B. Z1 = Z2 D. N1与匕2的大小无法比拟8.如图，ZAOB=ZAOC f ZBOC= 110° , ZAOB= ____________________D CO B角的相邻斜边重合，用铅笔沿曲，EQ画线，移开三角板，延长DE与AB交于点A, ZDAB= _________ .C二. 选择题14.以下说法正确的选项是（）A.不大于90的角是锐角B.一个钝角减去比它小的钝角，差是锐角C・钝角与锐角的差小于直角D.两个锐角的和是钝角15.以下说法错误的选项是（）A.角的大小与角的边画出局部的长短没有关系B.角的大小与它们的度数大小是一致的C.角的和差倍分的度数等于它们的度数的和差倍分D.假设ZA+ZB>ZC,那么ZA—定大于/C16.用一副三角板不能画出（）A.75°角B. 135°角C. 160°角D. 105°角17.如果Z1 - Z2=Z3,且Z4+Z2=Z1,那么N3和匕4间的关系是（）A.Z3>Z4B. Z3 = Z4C. Z3<Z4D.不确定18.在ZAOB的内部任取一点C,作射线OC,那么有（）A. ZAOC=ZBOCB. ZAOOZBOCC. ZBOC> ZAOBD. ZAOB> ZAOC三. 解答题19.如图，把ZAOB绕着。

角的比较与运算同步练习练习1、如图所示：（1）∠COD=-，或-。

（2）如果∠AOB=∠COD，则∠AOC与∠BOD的大小关系如何？2、如图所示：∠1：∠2：∠3：∠4=1：2：3：4，求∠1、∠2、∠3、∠4的度数？3、已知一条直线OA，若从点O再引两条射线OB和OC，使角AOB为60度，角BOC为20度，求角AOC 的度数。

4、如图，已知：∠BOC=2∠AOB，OD平分∠AOC，∠BOD=140求：∠AOB的度数。

C D BO A5.如图，OB是∠AOC的平分线，OD是∠COE的平分线。

(1)若∠AOC=800 ，求∠BOC的度数；(2)若∠AOC=800 ，∠COE=500，求∠BOD的度数。

E D C BOA∠AOB=390，∠BOC=210，则∠AOC的度数是多少？为什么？1.互补的两个角可以都是（）2.如图，OC是平角∠AOB的平分线，OD、OE分别是∠AOC和∠BOC的平分线，图中和∠COD互余的角有（）个。

A.1B.2 CD C EA O B3.如图，∠AOC=∠BOD=900，∠AOB=620，求∠COD的度数。

D C BO A4.6点30分，时针和分针的夹角为。

∠A与∠B都是锐角，∠A的补角是∠A的余角的3倍，∠B的补角比∠A的余角的3倍大240，求∠A、∠B 的度数.课堂练习请使用量角器、刻度尺画出下列点的位置。

（1）点A在点O的北偏东300的方向上，离点O的距离为3cm。

（2）点B在点O的南偏西600的方向上，离点O的距离为4cm。

（3）点C在点O的西北方向上，同时在点B的正北方向上。

( 4 ) 如图，若已知∠1+∠2=900，∠2+∠3=900，问∠1和∠3是什么关系？为什么？若∠2和∠4相等，则∠1和∠4要满足什么关系？为什么？（5）如图，O 是直线AB 上一点，∠AOB=∠FOD=900，OB 平分∠COD,图中与∠DOE 互余的角有哪些？与∠DOE 互补的角有哪些？ A 1 2 3 4 B C C A BDEF O。

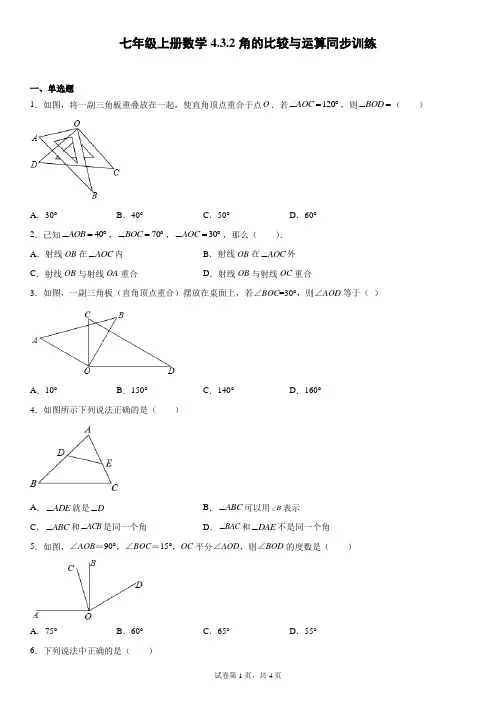
七年级上册数学4.3.2角的比较与运算同步训练一、单选题1．如图，将一副三角板重叠放在一起，使直角顶点重合于点O ．若120AOC ∠=︒，则BOD ∠=（ ）A ．30°B ．40°C ．50°D ．60°2．已知40AOB ∠=︒，70BOC ∠=︒，30AOC ∠=︒，那么（ ）．A ．射线OB 在AOC ∠内B ．射线OB 在AOC ∠外 C ．射线OB 与射线OA 重合D ．射线OB 与射线OC 重合3．如图，一副三角板（直角顶点重合）摆放在桌面上，若∠BOC =30°，则∠AOD 等于（ ）A ．10°B ．150°C ．140°D ．160°4．如图所示下列说法正确的是（ ）A ．ADE ∠就是D ∠B ．ABC ∠可以用B 表示 C ．ABC ∠和ACB ∠是同一个角D ．BAC ∠和DAE ∠不是同一个角5．如图，∠AOB ＝90°，∠BOC ＝15°，OC 平分∠AOD ，则∠BOD 的度数是（ ）A ．75°B ．60°C ．65°D ．55°6．下列说法中正确的是（ ）①两条射线组成的图形叫做角；②角的大小与边的长短无关；③若线段AC BC =，则点C 是线段AB 的中点；④将一根细木条固定在墙上，至少需要两根钉子，是因为两点确定一条直线．A ．1个B ．2个C ．3个D ．4个7．下列图形中，表示南偏西60︒的射线是（ ）．A ．B ．C ．D ．8．如图：∠AOB ：∠BOC ：∠COD ＝2：3：4，射线OM 、ON ，分别平分∠AOB 与∠COD ，又∠MON ＝84°，则∠AOB 为（ ）A ．28°B ．30°C ．32°D ．38°二、填空题9．计算： （1）33.21︒=_________︒_________'_________''；（2）57.32︒=_________︒_________'_________''；（3）3430'︒=_________︒；（4）5618'︒=_________︒．10．将一副直角三角尺如图放置，若155BOC ∠=︒，则AOD ∠=________︒．11．如图，在灯塔O 处观测到轮船A 位于北偏西50°的方向，同时轮船B 在南偏东15°的方向，那么AOB ∠=________．12．计算：35°45′＋72°19′＝___________．13．下面各个图形中，分别有多少个小于平角的角，请用适当的方法表示这些角．（1）图（1）中共有_______个小于平角的角，这些角分别是________；（2）图（2）中共有_______个小于平角的角，这些角分别是________；（3）图（3）中共有_______个小于平角的角，这些角分别是________．14．如图1:2:31:3:4∠∠∠=，440∠=︒，则1∠=________︒，2∠=________︒，3∠=________︒．15．如图，B 处在A 处的南偏西42°方向，C 处在A 处的南偏东30°方向，C 处在B 处的北偏东72°方向，则∠ACB 的度数是______．16．从点O 出发的三条射线OA 、OB 、OC ，使得2AOB AOC ∠=∠，且50AOB ∠=︒，则BOC ∠的度数为________．三、解答题17．观察常用时钟，回答下列问题：（1）下午2时整，时针和分针构成多少度的角？（2）时针多长时间转一圈？它转动的速度是每小时多少度？（3）从7:00到7:40，分针转动了多少度？18．如图，货轮与灯塔相距40n mile ，如何用方向和距离描述灯塔相对于货轮的位置？反过来，如何用方向和距离描述货轮相对于灯塔的位置？19．已知：如图①所示，OC 是AOB ∠内部一条射线，且OD 平分AOC ∠，OE 平分BOC ∠．（1）若80AOC ∠=︒，50BOC ∠=︒，则EOD ∠的度数是______．（2）若AOC α∠=，BOC β∠=，求EOD ∠的度数，并根据计算结果直接写出EOD ∠与AOB ∠之间的数量关系．（写出计算过程）（3）如图③所示，射线OC 在AOB ∠的外部，且OD 平分AOC ∠，OE 平分BOC ∠．试着探究EOD ∠与AOB ∠之间的数量关系．（写出详细推理过程）。

4.4 角的比较和运算5分钟训练 (预习类训练，可用于课前)1.若∠1与∠2互补，则∠1+∠2=_______，若∠1与∠2互余，则∠1+∠2=______.30°角的余角为______，补角为_____，70°39′角的余角为_____，补角为______.若一个角的度数为x(x ＜90°),则它的余角是______,若一个角的度数为x(x ＜180°),则它的补角是______.思路解析：利用两角互余即两角相加等于90°，两角互补即两角相加等于180°求解. 答案:180° 90° 60° 150° 19°21′ 109° 21′ 90°-x 180°-x2.如图4-4-1：O 是直线AB 上的一点，OC 是∠AOB 的平分线，①∠AOD 的补角是______；②∠AOD 的余角是______；③∠DOB 的补角是______.思路解析：由图可知∠AOB=180°，∠AOC=∠COB =90°，根据补角、余角的概念可求解. 答案:①∠DOB ②∠DOC ③∠AOD3.如图4-4-2：（1）∠AOC=∠（ ）+∠（ ）；（2）∠AOB=∠（ ）-（ ）=∠（ ）-∠（ ）；（3）若∠AOB=∠COD ，则∠AOC=（ ）.图4-4-1 图4-4-2思路解析：仔细观察图中各个角的关系是解决本题的关键.答案:（1）AOB BOC （2）AOC BOC AOD BOD （3）BOD10分钟训练(强化类训练，可用于课中)1.如图4-4-3：如果OC ，OD 把∠AOB 三等份，那么∠COD=（ ）∠AOB ，∠AOD=（ ）∠AOB ，∠AOB=（ ）∠AOD.图4-4-3思路解析：由条件知∠AOC=∠COD=∠BOD.答案: 13 23 322.填空:(1)77°42′+34°45′=______;(2)108°18′—56°23′=_______;(3)180°—(34°54′+21°33′)=______.思路解析：度、分、秒之间的进率为60，按照小学竖式计算(单位对齐).答案:（1）112°27′ （2）51°55′ （3）123°33′3.在∠AOB 内部任取一点C ，作射线OC ，那么一定有( )A.∠AOB＞∠ＡＯＣＢ.∠ＡＯＣ＞∠ＢＯＣＣ.∠ＢＯＣ＝∠ＡＯＢＤ.∠ＡＯＣ＝∠ＢＯＣ思路解析：作出图形，通过观察即可得出答案.答案:A4.判断：(1)一个角的余角一定是锐角;( )(2)一个角的补角一定是钝角;( )(3)一个角的补角不能是直角;( )(4)∠1+∠2+∠3=90°，那么∠1、∠2、∠3互为余角.( )思路解析：因为两角相加等于90°，那么这两个角互余，所以互余的两个角必都是锐角，所以(1)对，(4)错;而两个角互补是指两角相加等于180°，所以锐角、直角、钝角都有补角，所以(2)，(3)都错.答案:（1）√（2）×（3）×（4）×5.如图4-4-4，射线OC为∠AOB的平分线，∠AOC=35°，则∠AOB是多少？图4-4-4解：因为OC为∠AOB的平分线，所以∠AOC=∠BOC=35°.∴∠AOB=70°.6.如图4-4-5,如果∠1=65°15′,∠2=78°30′,∠3是多少度?图4-4-5思路解析：充分利用三角和为一个平角来解决问题.解：因为∠1，∠2，∠3组成一个平角，所以∠3=180°-∠1-∠2=36°15′.快乐时光水果摊一位挑剔的顾客来到一个小食品店，看到新送来的一批新鲜水果，他对售货员说：“给我两公斤橙子，并用纸把每个橙子分别包起来。

新人教版七年级数学上册《角的比较与运算》测试题学习要求会比较两个角的大小，能进行角的运算(和、差、倍、分)．理解角的平分线以及直角、锐角、钝角的概念．课堂学习检测一、填空题1．要比较∠α 和∠β 的大小，可先让∠α 的顶点与∠β 的顶点______，∠α 的始边与∠β 的始边也______，并且∠α 的终边与∠β 的终边都在它们的始边的同一侧． 若∠α 的终边落在∠β 的内部，则称∠α ______∠β ； 若∠α 的终边落在∠β 的外部，则称∠α ______∠β ； 若∠α 的终边恰与∠β 的终边重合，则称∠α ______∠β ．(如图所示，∠AOB ＝α ；∠AOC ＝β )2．如图，若OC 是∠AOB 的平分线，则______＝______；或______＝______21=______； 或______＝2______＝2______．3．如图，OM 是∠AOB 的平分线且∠AOM ＝30°，则∠BOM ＝______；∠AOB ＝______．4．如图，在横线上填上适当的角：(1)∠AOC ＝______＋______； (2)∠AOD －∠BOD ＝______； (3)∠BOC ＝______－∠COD ；(4)∠BOC ＝∠AOC ＋______－______． 5．按图填空：(1)∠ABC 是∠ABD 与∠DBC 的______； (2)∠BDC 是∠ADC 与∠ADB 的_______． 6．如图，(1)若∠AOB ＝∠COD ，则∠AOC ＝∠______． (2)若∠AOC ＝∠BOD ， 则∠______＝∠______．二、选择题7．在小于平角的∠AOB 的内部取一点C ，并作射线OC ，则一定存在( )． (A)∠AOC ＞∠BOC (B)∠AOC ＝∠BOC (C)∠AOB ＞∠AOC (D)∠BOC ＞∠AOC 8．如图，∠AOB ＝∠COD ，则( )．(A)∠1＞∠2 (B)∠1＝∠2 (C)∠1＜∠2(D)∠1与∠2的大小无法比较 9．射线OC 在∠AOB 的内部，下列四个式子中不能判定OC 是∠AOB 的平分线的是( )． (A)∠AOB ＝2∠AOC (B)∠BOC ＝∠AOC(C)∠AOC 21∠AOB (D)∠AOC ＋∠BOC ＝∠AOB 10．不能用一副三角板拼出的角是( )．(A)120° (B)105° (C)100° (D)75°11．如图，OC 是∠AOB 的平分线，OD 平分∠AOC ，且∠COD ＝25°，则∠AOB ＝( )．(A)100° (B)75°(C)50° (D)20°12．如果∠AOB ＝34°，∠BOC ＝18°，那么∠AOC 的度数是( )．(A)52° (B)16° (C)52°或16° (D)52°或18° 13．如图，射线OD 是平角∠AOB 的平分线，∠COE ＝90°，那么下列式子中错误的是( )．(A)∠AOC ＝∠DOE (B)∠COD ＝∠BOE (C)∠AOD ＝∠BOD (D)∠BOE ＝∠AOC 14．已知α 、β 是两个钝角，计算)(61β+a 的值，四位同学算出了四种不同的答案，分别为24°，48°，76°，86°，其中只有一个答案是正确的，那么你认为正确的是( ) (A)24° (B)48° (C)76° (D)86° 三、解答题15．下面是小马虎解的一道题．题目：在同一平面上，若∠BOA ＝70°，∠BOC ＝15°，求∠AOC 的度数． 解：根据题意可画出下图．∵∠AOC ＝∠BOA －∠BOC＝70°－15° ＝55°，∴∠AOC ＝55°．若你是老师，会给小马虎满分吗?若会，说明理由．若不会，请将小马虎的错误指出，并给出你认为正确的解法．综合、运用、诊断16．如图，OT 平分∠AOB ，也平分∠COD ，那么∠AOT ＝∠______，∠AOC ＝∠______， ∠AOD ＝∠______17．如图，OA ⊥OB ，OC ⊥OD ，∠AOD ＝146°，则∠BOC ＝______．18．读语句画图并填空：画平角∠AOC ，用量角器画∠AOC 的平分线OB ，因为OB 平分∠AOC ，所以∠AOB =∠=AOC 21_______，再用量角器画∠BOC 的平分线OD ，图中∠AOD ＝∠______＋∠______＝______°．19．作图．(1)用一副三角板可以画出多少个小于平角的角?请用一副三角板画出15°，75°角．(2)作∠MPQ 的平分线PR ，则∠______＝∠______21=∠______．(3)利用圆规和直尺画一个角．已知：∠AOB ，求作：∠A ′O ′B ′，使得∠A ′O ′B ′＝∠AOB ．20．如图，OD 、O E 分别是∠AOC 和∠BOC 的平分线，∠AOD ＝40°，∠BOE ＝25°，求∠AOB 的度数．解：∵OD 平分∠AOC ，OE 平分∠BOC ，∴∠AOC ＝2∠AOD ，∠BOC ＝2∠______．∵∠AOD ＝40°，∠BOE ＝25°， ∴∠BOC ＝______， ∠AOC ＝______． ∴∠AOB ＝____．21．已知：如图，∠ABC ＝∠ADC ，DE 是∠ADC 的平分线，BF 是∠ABC 的平分线．求证：∠2＝∠3．证明：∵DE 是∠ADC 的平分线，∴∠2＝______．∵BF 是∠ABC 的平分线， ∴∠3＝______．又∵∠ABC ＝∠ADC ， ∴∠2＝∠3．拓展、探究、思考22．已知：∠AOB ＝31.5°，∠BOC ＝24.3°，求∠AOC 的度数．23．如图，从O 点引四条射线OA 、OB 、OC 、OD ，若∠AOB ，∠BOC ，∠COD ，∠DOA度数之比为1∶2∶3∶4．(1)求∠BOC 的度数．(2)若OE 平分∠BOC ，OF 、OG 三等分∠COD ，求∠EOG ．24．如图，∠AOB 的平分线为OM ，ON 为∠MOA 内的一条射线，OG 为∠AOB 外的一条射线，某同学经过认真的分析，得出一个关系式是∠MON ＝21(∠BON －∠AON )，你认为这个同学得出的关系式是正确的吗?若正确，请把得出这个结论的过程写出来。

人教版七年级数学上册《4.3.2 角的比较与运算》课时练1．在∠AOB的内部取一点C，作射线OC，则一定存在（）A．∠AOB＞∠AOC B．∠AOC＞∠BOCC．∠BOC＞∠AOC D．∠AOC＝∠BOC2．如图所示，若∠AOB＝∠COD，则（）第2题图A．∠1>∠2 B．∠1＝∠2C．∠1<∠2 D．∠1与∠2的大小关系不能确定3．如图，OC为∠AOB内的一条射线，下列条件中不能确定OC平分∠AOB的是（）A．∠AOC＝∠BOCB．∠AOB＝2∠AOCC．∠AOC＋∠COB＝∠AOBD．∠BOC＝12∠AOB 第3题图4．如图，已知O是直线AB上一点，∠1＝40°，OD平分∠BOC，则∠2的度数是（）A．20°B．25°C．30°D．70°第4题图5．借助一副三角尺，你能画出下面哪个度数的角？（）A．65°B．75°C．85°D．95°6．已知∠AOB＝30°，∠BOC＝45°，则∠AOC等于（）A．15°B．75°C．15°或75°D．不能确定7．如图所示，（1）∠BAC＝____________＋____________；（2）∠ABE＝____________＋____________；（3）∠2＝________－________－________；（4）∠ADB＝____________－____________．第7题图8．如图所示，已知∠AOD＝120°，∠AOC＝2∠AOB＝60°，那么∠BOD=_______度．第8题图9．计算下列各题．（1）98°45′36″＋71°22′34″＝____________；（2）52°37′－31°45′12″＝____________；（3）13°24′15″×5＝____________；（4）58°34′16″÷4＝____________．10．如图，∠BOA＝90°，OC平分∠BOA，OA平分∠COD，求∠BOD的大小．第10题图11．如图所示，已知∠AOC＝∠BOD＝100°，且∠AOB∶∠AOD＝2∶7，求∠BOC和∠COD的度数．第11题图12．如图，OC，OD是∠AOB内的两条射线，OM平分∠AOC，ON平分∠DOB，∠AOB＝120°，∠MON＝80°，则∠COD＝__________．第12题图13．如图，O为直线AB上一点，OD平分∠AOC，∠DOE＝90°.（1）请你数一数，图中有________个小于平角的角；（2）若∠AOC＝50°，则∠COE的度数为________，∠BOE的度数为________；（3）猜想：OE是否平分∠BOC？请通过计算说明你猜想的结论的正确性．第13题图14．一题多变：（1）如图1，已知∠AOB＝80°，OC是∠AOB的平分线，OD平分∠BOC，OE平分∠AOC，求∠DOE的度数；（2）如图2，在（1）中，把“OC是∠AOB的平分线”改为“OC为∠AOB 内任意一条射线”，其他条件不变，试求∠DOE的度数；（3）如图3，在（1）中，把“OC是∠AOB的平分线”改为“OC是∠AOB 外的一条射线（点A与点C在直线OB同侧）”，其他条件不变，能否求出∠DOE的度数，说明理由；（4）在（3）中，若把“∠AOB＝80°”改为“∠AOB＝α”，其他条件不变，求此时∠DOE的度数，从中你得出什么规律？第14题图参考答案1—5．ABCDB6．C7．（1）∠1∠2（2）∠ABD∠DBE（3）∠BAD∠1∠3（4）∠ADC∠BDC8．1509．（1）170°8′10″（2）20°51′48″（3）67°1′15″（4）14°38′34″10．因为OC平分∠BOA，所以∠AOC＝12∠ABO.因为∠AOB＝90°，所以∠AOC＝12×90°＝45°.因为OA平分∠COD，所以∠AOD＝∠AOC＝45°.所以∠BOD＝∠AOB＋∠AOD＝90°＋45°＝135°.11．设∠AOB和∠AOD分别为2x°、7x°，由题意，得2x＋100＝7x，解得x＝20.则∠AOB＝40°，∠AOD＝140°.所以∠BOC＝∠AOC－∠AOB＝60°，∠COD＝∠BOD－∠BOC＝40°.12．40°13．（1）9（2）65°65°（3）结论：OE平分∠BOC.设∠AOC＝2α.因为OD平分∠AOC，∠AOC＝2α，所以∠AOD＝∠COD＝12∠AOC＝α.因为∠DOE＝90°，所以∠COE＝∠DOE－∠COD＝90°－α.因为∠BOE＝180°－∠DOE－∠AOD＝180°－90°－α＝90°－α，所以∠COE＝∠BOE，即OE平分∠BOC.14．（1）因为OD平分∠BOC，OE平分∠AOC，所以∠DOC＝12∠BOC，∠COE＝12∠AOC，又因为∠DOE＝∠DOC＋∠COE，所以∠DOE＝12（∠BOC＋∠AOC）＝12∠AOB＝40°；（2）同（1）的求法可知，∠DOE＝40°；（3）可以．理由如下：因为OE平分∠AOC，OD平分∠BOC，所以∠AOE＝12∠AOC，∠COD＝12∠BOC，所以∠DOE＝∠COD－∠COE＝12（∠BOC－∠AOC）＝12∠AOB＝40°；（4）∠DOE＝12α.规律：不管射线OC在∠AOB的内部还是外部，都有∠DOE＝12α.。

4.3.2角的比较与运算1.如图,在∠AOB内部任取一点C,连接OC,则下列结论一定成立的是()A.∠AOC>∠BOCB.∠BOC<∠AOBC.∠AOC<∠BOCD.∠BOC>∠AOB2.如图,若∠AOC=∠BOD,那么∠AOD与∠BOC的关系是()A.∠AOD>∠BOCB.∠AOD<∠BOCC.∠AOD=∠BOCD.无法确定3.∠α和∠β的顶点和一边都重合,另一边都在公共边的同侧,且∠α>∠β,那么∠α的另一边落在∠β的 ()A.另一边上B.内部C.外部D.内部或另一边上4.小明同学用一副三角尺画出了许多不同度数的角,但下列哪个度数的角画不出来()A.135°B.120°C.75°D.25°5.已知∠AOB=70°,以O为端点作射线OC,使∠AOC=42°,则∠BOC的度数为()A.28°B.112°C.28°或112°D.68°6.已知∠AOB=60°,∠AOC=∠AOB,射线OD平分∠BOC,则∠COD的度数为()A.20°B.40°C.20°或30°D.20°或40°7.角α,β都是钝角,甲、乙、丙、丁四人计算(α+β)的结果依次为12°,44°,66°,88°,其中只有一人计算正确,那么算出正确答案的是()A.甲B.乙C.丙D.丁8.如图,∠AOC为直角,OC是∠BOD的平分线,且∠AOB=34°,则∠AOD的度数为()A.124°B.136°C.146°D.158°8.已知三条不同的射线OA,OB,OC,有下列条件,其中能确定OC平分∠AOB的有()①∠AOC=∠BOC;②∠AOB=2∠AOC;③∠AOC+∠BOC=∠AOB;④∠BOC=∠AOB.A.1个B.2个C.3个D.4个10.如图点B,O,D在同一条直线上,若∠1=15°,∠2=105°,则∠AOC=°.11.如图,O是直线AB上的一点,OC,OD,OE是从点O引出的三条射线,且∠1∶∠2∶∠3∶∠4=1∶2∶3∶4,则∠5=°.12.比较两个角的大小,有以下两种方法:①用量角器量度两个角的大小,用度数表示,则度数大的角大;②构造图形,若一个角能包含(或覆盖)另一个角,则这个角大.对于如图4-3-11所示给定的∠ABC与∠DEF,用以上两种方法分别比较它们的大小.图4-3-1113.如图,∠ABC是平角,过点B作一条射线BD将∠ABC分成∠DBA和∠DBC,当∠DBA是什么角时,满足下列要求:(1)∠DBA<∠DBC;(2)∠DBA>∠DBC;(3)∠DBA=∠DBC.14.计算:(1)48°39'+67°31'; (2)78°-47°34'56″;(3)22°16'×5; (4)42°15'÷5.15.计算:(1)40°26'+30°30'30″÷6;(2)13°53'×3-32°5'31″.16.如图已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠AOC和∠BOC的度数.17.如图∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE,求∠COE的度数.18.如图,∠AOB=90°,∠AOC=30°,且OM平分∠BOC,ON平分∠AOC.(1)求∠MON的度数;(2)若∠AOB=α,其他条件不变,求∠MON的度数;(3)若∠AOC=β(β为锐角),其他条件不变,求∠MON的度数;(4)从上面的结果中,你得出了什么结论?答案1.B2.C3.C4.D5.C6.D7.B8.C9.A10.9011.6012.解:①用量角器量度∠ABC=50°,∠DEF=70°,所以∠DEF>∠ABC.②如图:把∠ABC的边BC和∠DEF的边EF重合,使点B和点E重合,BA和DE在EF的同侧, 从图形上可以看出∠DEF能包含∠ABC,即∠DEF>∠ABC.13.解:(1)当∠DBA是锐角时,∠DBC是钝角,满足∠DBA<∠DBC.(2)当∠DBA是钝角时,∠DBC是锐角,满足∠DBA>∠DBC.(3)当∠DBA是直角时,∠DBA=∠DBC=90°,满足∠DBA=∠DBC.14.解:(1)48°39'+67°31'=116°10'.(2)78°-47°34'56″=30°25'4″.(3)22°16'×5=111°20'.(4)42°15'÷5=8°27'.15.解:(1)40°26'+30°30'30″÷6=40°26'+5°5'5″=45°31'5″.(2)13°53'×3-32°5'31″=41°39'-32°5'31″=9°33'29″.16.解:因为OE平分∠AOB,OF平分∠BOC,所以∠BOE=∠AOB=×90°=45°,∠COF=∠BOF=∠BOC.因为∠BOF=∠EOF-∠BOE=60°-45°=15°,所以∠BOC=2∠BOF=30°.所以∠AOC=∠BOC+∠AOB=30°+90°=120°.17.解:因为∠AOB=90°,OC平分∠AOB,所以∠BOC=∠AOB=45°.因为∠BOD=∠COD-∠BOC=90°-45°=45°,∠BOD=3∠DOE,所以∠DOE=15°.所以∠COE=∠COD-∠DOE=90°-15°=75°. 18.解:(1)因为∠AOB=90°,∠AOC=30°, 所以∠BOC=120°.因为OM 平分∠BOC ,ON 平分∠AOC , 所以∠COM=60°,∠CON=15°. 所以∠MON=∠COM-∠CON=45°. (2)因为∠AOB=α,∠AOC=30°, 所以∠BOC=α+30°.因为OM 平分∠BOC ,ON 平分∠AOC , 所以∠COM=+15°,∠CON=15°. 所以∠MON=∠COM-∠CON=. (3)因为∠AOB=90°,∠AOC=β, 所以∠BOC=90°+β.因为OM 平分∠BOC ,ON 平分∠AOC , 所以∠COM=45°+,∠CON=. 所以∠MON=∠COM-∠CON=45°.(4)从上面的结果中,得出以下结论:∠MON 的度数始终等于∠AOB 的度数的一半,而与∠AOC 的度数无关.1、在最软入的时候，你会想起谁。

人教版七年级数学上册《6.3.2角的比较与运算》同步测试题带答案一、单选题1．把2.36︒用度、分、秒表示，正确的是（ ）A ．221'36"︒B ．218'36''︒C ．230'60"︒D ．23'6"︒2．若383A '∠=︒，38.3B ∠=︒则（ ）A ．AB ∠<∠ B ．A B ∠>∠C ．A B ∠=∠D ．无法确定3．用一副三角尺的两个角不能拼成（ ）度的角．A ．15B ．105C ．110D ．1204．若1290∠+∠=︒，15825'∠=︒那么∠2的度数是（ ）A ．3175'︒B ． 3135'︒C ．4175'︒D ．4125︒'5．如图，已知:2:3AOB BOC ∠∠=，30AOB ∠=︒那么AOC ∠=（ ）A ．45︒B ．50︒C ．60︒D ．75︒6．如下图2BOC AOB ∠=∠，OP 平分AOB ∠，已知12AOP ∠=︒，则POC ∠=（ ）A ．60︒B ．72︒C ．78︒D ．84︒7．入射光线和平面镜的夹角为40°，转动平面镜，使入射角减小20°，反射光线与入射光线的夹角和原来相比较将（ ）A ．减小40°B ．增大40°C ．减小20°D ．不变8．如图，设锐角AOB ∠的度数为α，若一条射线平分AOB ∠，则图中所有锐角的和为2α．若四条射线五等分AOB ∠，则图中所有锐角的和为( )A ．7αB ．6αC ．5αD ．4a二、填空题9．若130.45︒∠=，23028︒'∠=则1∠ 2∠（用“＞”“=”“＜”填空）．10．将一副直角三角尺如图放置，若22AOD ∠=︒，则BOC ∠的大小为 ．11．如图，已知()585AOB BOC x ∠=︒∠=+︒，， ()27AOC x ∠=-︒那么AOC ∠= 度．12．小明从O 点出发向北偏西40︒走了500米到达A 点，小丽从O 点出发向南偏东40︒走了300米到达B 点，这时A 、B 两点之间的距离是 米．13．如图，已知点O 是直线AB 上一点，OC OD OM ON 、、、为从点O 引出的四条射线，若30BOD ∠=︒87COD AOC ∠=∠ 90MON ∠=︒ 则AON ∠与COM ∠之间的数量关系是 ；三、解答题14．计算：(1)89352020''︒+︒（结果用度、分、秒表示）．(2)123246036''︒-︒（结果用度表示）．15．如图，直线CD ，EF 交于点O ，OA ，OB 分别平分COE ∠和DOE ∠，且3OGB ∠=∠．(1)求证：1290∠+∠=︒；(2)若332∠=∠，求1∠的度数．16．已知直线AB 与CD 相交于点O ，且OM 平分AOC ∠．(1)如图1，若ON 平分BOC ∠，求MON ∠的大小；(2)如图2，若MON α∠=，13CON BON ∠=∠求BON ∠的大小．（用含α的式子表示） 参考答案 题号1 2 3 4 5 6 7 8 答案 A A C B DA A A1．【答案】A【分析】根据大单位化小单位除以进率，可得答案．【详解】解：2.36°＝2°＋0.36×60′＝2°21′＋0.6×60″＝2°21′36″故选：A ．【点睛】此题主要考查度、分、秒的转化运算，进行度、分、秒的转化运算，注意以60为进制． 2．【答案】A【分析】将∠A 或∠B 的大小统一成用度或用度分秒表示的形式，即可得出结论．【详解】解：∠∠A =38°3′，∠B =38.3°=38°18′故选：A ．【点睛】本题主要考查了角的大小比较，统一角的大小单位是解决问题的关键．3．【答案】C【分析】本题考查了角的计算．用三角板拼特殊角其实质是角的和差运算，理解题意是关键．用三角板画出角，无非是用角度加减法．根据选项一一分析，排除错误答案．【详解】解：A ．15︒的角453015︒-︒=︒；故本选项不符合题意；B ．105︒的角4560105︒+︒=︒；故本选项不符合题意；C ．110︒的角，无法用三角板中角的度数拼出；故本选项符合题意；D ．120︒的角9030120︒+︒=︒；故本选项不符合题意．故选C ．4．【答案】B【分析】本题考查角度的加减计算．根据角度的加减法计算即可，注意进率为60．【详解】解：根据题意2901896058253135'''∠=︒-∠=︒-︒=︒．故选：B ．5．【答案】D【分析】本题考查角的有关计算，按比例分配求出45BOC ∠=︒是解答的关键．根据:2:3AOB BOC ∠∠=求出45BOC ∠=︒，然后利用AOC AOB BOC ∠=∠+∠求解即可．【详解】解：∠:2:3AOB BOC ∠∠= 30AOB ∠=︒∠45BOC ∠=︒∠75AOCAOB BOC ．故选：D ．6．【答案】A【分析】本题主要考查了几何图形中角度的计算，角平分线的定义，先由角平分线的定义得到12224BOP AOP AOB AOP =∠=︒==︒∠，∠∠，再由已知条件得到248BOC AOB ∠=∠=︒，则60POC BOC BOP =+=︒∠∠∠． 【详解】解：∠OP 平分AOB ∠ 12AOP ∠=︒∠12224BOP AOP AOB AOP =∠=︒==︒∠，∠∠∠248BOC AOB ∠=∠=︒∠60POC BOC BOP =+=︒∠∠∠7．【答案】A【分析】分别求出平面镜转动前后反射光线与入射光线的夹角，再对两者进行比较即可得到解答．【详解】解：入射光线与平面镜的夹角是40°，所以入射角为90°−40°=50°．根据光的反射定律，反射角等于入射角，反射角也为50°所以入射光线与反射光线的夹角是100° ．入射角减小20°，变为50°−20°=30°，所以反射角也变为30°此时入射光线与反射光线的夹角为60°．则反射光线与入射光线间的夹角和原来比较将减小40°．故选：A ．【点睛】本题考查角度与光反射的综合应用，熟练掌握光的反射规律及角度的计算方法是解题关键． 8．【答案】A 【分析】本题考查了角度的计算，角的数量问题，根据题意可得每一个小角的度数为15α，进而将所有角的度数相加即可求解．【详解】∠四条射线五等分AOB ∠∠每个小角的度数为15α．如图图中所有锐角的和为()()AOC COD DOE EOF BOF AOD COE DOF BOE ∠+∠+∠+∠+∠+∠+∠+∠+∠+()()AOE COF BOD AOF BOC AOB ∠+∠+∠+∠+∠+∠=123454325555ααααα⨯+⨯+⨯+⨯+ 7α=故选：A ．9．【答案】＜【分析】将∠1进行换算，再和∠2比较即可判断大小．【详解】解：∠0.45°=27′∠∠1=30.45°=30°+0.45°=30°27′∠∠2=30°28′∠∠1＜∠2．故答案为：＜．【点睛】本题主要考查度分秒的换算，换成形式一样的即可比较大小．10．【答案】158︒【分析】根据角的和差关系求解即可；【详解】由题意得：90COD ∠=︒ 90AOB ∠=︒∠22AOD ∠=︒∠902268AOC COD AOD ∠=∠-∠=︒-︒=︒∠6890158BOC AOC AOB ∠=∠+∠=︒+︒=︒故答案为：158︒【点睛】本题主要考查角的和差关系，熟练掌握角的和差关系是解此类题的关键．11．【答案】133【分析】本题考查了几何图形中角度计算问题，结合图形得出AOC AOB BOC ∠=∠+∠，代数进行计算，得出x 的值，然后把x 的值代入()27AOC x ∠=-︒进行计算，即可作答．【详解】解：∠()585AOB BOC x ∠=︒∠=+︒， ()27AOC x ∠=-︒ 且AOC AOB BOC ∠=∠+∠∠()()27585x x -︒=︒++︒∠70x =则把70x =代入()27AOC x ∠=-︒∠133AOC ︒∠=故答案为：133．12．【答案】800【分析】本题考查了方位角，线段的和差，角的和差，由方位角的定义得40AOD BOC ∠=∠=︒，由角的和差得 180AOD DOE BOE ∠+∠+∠=︒，可得A 、O 、B 三点在同一条直线上，由线段的和差即可求解；理解方位角，会判断三点共线时是解题的关键．【详解】解：如图由题意得：40AOD BOC ∠=∠=︒90DOE ∠=︒500OA =300OB =9040BOE ∴∠=︒-︒50=︒AOD DOE BOE ∴∠+∠+∠409050=︒+︒+︒180=︒∴A 、O 、B 三点在同一条直线上AB OA OB ∴=+500300=+800=(米)故答案：800．13．【答案】20AON COM ∠+︒=∠ 【分析】本意考查了角的计算，根据87COD AOC ∠=∠，设78AOC x COD x ∠=∠=，，由180AOC COD BOD ∠︒+∠+∠=可求出x 的值，再由AON MON AOC COM ∠+∠=∠+∠即可得出答案．【详解】解：设78AOC x COD x ∠=∠=，由180AOC COD BOD ∠︒+∠+∠=7830180x x ∴++︒=︒10x ∴=︒即7080AOC COD ∠=︒∠=︒，AON MON AOC COM ∠+∠=∠+∠9070AON COM ∴∠+︒=︒+∠即20AON COM ∠+︒=∠故答案为：20AON COM ∠+︒=∠．14．【答案】(1)10955'︒(2)62.8︒【分析】本题考查了度分秒的换算，熟练掌握度分秒的进制是解题的关键．（1）根据度分秒的进制进行计算，即可解答；（2）根据度分秒的进制进行计算，即可解答．【详解】（1）89352020''︒+︒10955'=︒；（2）123246036''︒-︒123.460.6=︒-︒62.8=︒．15．【答案】(1)1290∠+∠=︒(2)54︒【分析】本题主要考查了角平分线的有关计算，平行线的判定以及性质，平角的定义，掌握这些定义以及性质是解题的关键．（1）由角平分线的定义得出11,22AOC COE BOD DOE ∠=∠∠=∠，由平角的定义得出180COE DOE ∠+∠=°，进而得出90AOC BOD ∠+∠=︒，再证明AB CD ∥，由平行线的性质可得出12AOC BOD ∠=∠∠=∠，，等量代换可得出1290∠+∠=︒．（2）由角平分线的定义和平行线的性质得出122BOD BOG DOG ∠=∠=∠=∠，设2x ∠=，则3323x ∠=∠=．根据平角的定义得出3180DOG ∠+∠=︒，代入计算得出2∠的度数，再根据（1）可求出1∠的度数．【详解】（1）证明OA ，OB 分别平分COE ∠和DOE ∠11,22AOC COE BOD DOE ∴∠=∠∠=∠． 180COE DOE ∠+∠=︒．()1111180902222AOC BOD COE DOE COE DOE ∴∠+∠=∠+∠=∠+∠=⨯︒=︒． 3OGB ∠=∠AB CD ∴∥．12AOC BOD ∴∠=∠∠=∠，．2190∴∠+∠=︒（2）OB 平分DOE ∠ AB CD ∥122BOD BOG DOG ∴∠=∠=∠=∠． 设2x ∠=，则3323x ∠=∠=．3180DOG ∠+∠=︒即32180x x +=︒解得36x =︒236∴∠=︒．1903654∴∠=︒-︒=︒16．【答案】(1)90︒ (2)2703BON α∠=-【分析】本题主要考查了角平分线的相关计算和角的和差倍分、解一元一次方程； （1）根据平角的定义，角的平分线的意义计算即可；（2）设设BON x ∠=︒，则13COM x α∠=-︒，由OM 平分AOC ∠得到1223AOC MOC x α⎛⎫∠=∠=-︒ ⎪⎝⎭，根据180AOC BON CON ∠+∠+∠=︒列方程解方程即可得到答案．【详解】（1）解：∠OM 平分AOC ∠，ON 平分BOC ∠ ∠12MOC AOC ∠=∠ 12CON BOC ∠=∠ ∠1()2MOC CON AOC BOC ∠+∠=∠+∠ ∠111809022MON AOB ∠=∠=⨯︒=︒． （2）设BON x ∠=︒ ∠1133CON BON x ∠=∠=︒ MON α∠= ∠13COM x α∠=-︒ ∠OM 平分AOC ∠ ∠1223AOC MOC x α⎛⎫∠=∠=-︒ ⎪⎝⎭ ∠180AOC BON CON ∠+∠+∠=︒ ∠11218033x x x α⎛⎫-++= ⎪⎝⎭ ∠2703x α=-∠2703BON α∠=-．。

人教版七年级上册4.3.2 角的比较与运算(270) 1.如图，点B，O，D在同一直线上，若∠1=15∘，∠2=105∘，则∠AOC=．2.如图，A，O，B是同一直线上的三点，OC，OD，OE是从点O引出的三条射线，且∠1∶∠2∶∠3∶∠4=1∶2∶3∶4，则∠5=度．3.计算：(1)48∘39′+67∘31′；(2)78∘−47∘34′56″；(3)22∘16′×5；(4)42∘15′÷5.4.计算：(1)40∘26′+30∘30′30″÷6；(2)13∘53′×3−32∘5′31″．5.计算：(13.9∘+5∘4′3″)×2−(6∘5′+2∘8′23″)．(结果用度、分、秒表示)6.如图，已知∠AOB=90∘，∠EOF=60∘，OE平分∠AOB，OF平分∠BOC，求∠AOC和∠BOC 的度数．7.如图，∠AOB=∠COD=90∘，OC平分∠AOB，∠BOD=3∠DOE,求∠COE的度数．8.如图，∠AOB=90∘，∠AOC=30∘，且OM平分∠BOC，ON平分∠AOC．(1)求∠MON的度数；(2)若∠AOB=α，其他条件不变，求∠MON的度数；(3)若∠AOC=β(β为锐角)，其他条件不变，求∠MON的度数；(4)从上面的结果中，你得出了什么结论？9.如图，在∠AOB内部任取一点C,则下列结论一定成立的是（）A.∠AOC>∠BOCB.∠BOC<∠AOBC.∠AOC<∠BOCD.∠BOC>∠AOB10.如图，OC是∠AOB的平分线，若∠AOC=75∘，则∠AOB的度数为（）A.145∘B.150∘C.155∘D.160∘11.计算：(1)179∘−72∘18′54″；(2)360∘÷7(精确到秒)．12.下列角度中，比20∘小的是（）A.19∘38′B.20∘50′C.36.2∘D.56∘13.∠α和∠β的顶点和一边都重合，另一边都在公共边的同侧，且∠α>∠β，那么∠α的另一边落在∠β的（）A.另一边上B.内部C.外部D.内部或另一边上14.比较两个角的大小，有以下两种方法(规则)：①用量角器量两个角的大小，用度数表示，角度大的角大；②构造图形，若一个角包含(或覆盖)另一个角，则这个角大．对于如图，给定的∠ABC与∠DEF，用以上两种方法分别比较它们的大小．注：构造图形时，作示意图(草图)即可．15.如图，∠ABC是平角，过点B作一条射线BD将∠ABC分成∠DBA和∠DBC，当∠DBA是什么角时，满足下列要求：(1)∠DBA<∠DBC；(2)∠DBA>∠DBC；(3)∠DBA=∠DBC．16.把两块三角板按如图所示那样拼在一起，则∠ABC等于（）A.90∘B.100∘C.105∘D.120∘17.小明同学用一副三角尺画出了许多不同度数的角，但下列哪个度数的角画不出来（）A.135∘B.120∘C.75∘D.25∘18.如图是一副特制的三角尺，用它们可以画出一些特殊角．在54∘，60∘，63∘，72∘，99∘，120∘，144∘，150∘，153∘，171∘的角中，能画出的角有（）A.7个B.8个C.9个D.10个19.已知∠AOB=70∘，以O为端点作射线OC，使∠AOC=42∘，则∠BOC的度数为（）A.28∘B.112∘C.28∘或112∘D.68∘20.角α，β都是钝角，甲、乙、丙、丁四人计算1(α+β)的结果依次为12∘，44∘，666∘，88∘，其中只有一人计算正确，那么算出正确答案的是（）A.甲B.乙C.丙D.丁参考答案1.【答案】:90∘【解析】:∵∠2=105∘，∴∠BOC=180∘−∠2=75∘，∴∠AOC=∠1+∠BOC=15∘+75∘=90∘2.【答案】:60【解析】:因为A，O，B是同一直线上的三点，即∠AOB=180∘，∠1∶∠2∶∠3=1∶2∶3，所以∠1=30∘，∠2=60∘，∠3=90∘.又因为∠1∶∠2∶∠3∶∠4=1∶2∶3∶4，所以∠4=120∘，∠5=180∘−120∘=60∘3(1)【答案】解：48∘39′+67∘31′=116∘10′(2)【答案】解：78∘−47∘34′56″=30∘25′4″(3)【答案】解：22∘16′×5=111∘20′(4)【答案】解：42∘15′÷5=8∘27′4(1)【答案】解：40∘26′+30∘30′30″÷6=40∘26′+5∘5′5″=45∘31′5″(2)【答案】解：13∘53′×3−32∘5′31″=41∘39′−32∘5′31″=9∘33′29″5.【答案】:解：(13.9∘+5∘4′3″)×2−(6∘5′+2∘8′23″)=18∘58′3″×2−8∘13′23″=37∘56′6″−8∘13′23″=29∘42′43″6.【答案】:解：∵OE平分∠AOB，OF平分∠BOC，∴∠BOE=12∠AOB=12×90∘=45∘，∠COF=∠BOF=12∠BOC．∵∠BOF=∠EOF−∠BOE=60∘−45∘=15∘，∴∠BOC=2∠BOF=30∘，∴∠AOC=∠BOC+∠AOB=30∘+90∘=120∘7.【答案】:解：∵∠AOB=90∘，OC平分∠AOB，∴∠BOC=12∠AOB=45∘.∵∠BOD=∠COD−∠BOC=90∘−45∘=45∘，∠BOD=3∠DOE，∴∠DOE=15∘，∴∠COE=∠COD−∠DOE=90∘−15∘=75∘8(1)【答案】解：∵∠AOB=90∘，∠AOC=30∘，∴∠BOC=120∘.∵OM平分∠BOC，ON平分∠AOC，∴∠COM=60∘，∠CON=15∘，∴∠MON=∠COM−∠CON=45∘(2)【答案】解：∵∠AOB=α，∠AOC=30∘，∴∠BOC=α+30∘.∵OM平分∠BOC，ON平分∠AOC，∴∠COM=α2+15∘，∠CON=15∘，∴∠MON=∠COM−∠CON=α2(3)【答案】解：∵∠AOB=90∘，∠AOC=β，∴∠BOC=90∘+β.∵OM平分∠BOC，ON平分∠AOC，∴∠COM=45∘+β2，∠CON=β2，∴∠MON=∠COM−∠CON=45∘(4)【答案】解：从上面的结果中，得出以下结论：∠MON的度数只与∠AOB的度数有关，而与∠AOC的度数无关9.【答案】:B10.【答案】:B【解析】:因为OC是∠AOB的平分线，∠AOC=75∘，所以∠AOB=2∠AOC=150∘. 故选B11(1)【答案】解：原式=178∘59′60″−72∘18′54″=106∘41′6″【解析】:解：原式=178∘59′60″−72∘18′54″=106∘41′6″(2)【答案】解：原式≈51∘25′43″12.【答案】:A【解析】:在四个选项中，只有19∘38′<20∘13.【答案】:C【解析】:若∠α>∠β，则∠α的另一边落在∠β的外部.故选 C.14.【答案】:解：①用量角器度量∠ABC=50∘，∠DEF=70∘，即∠DEF>∠ABC；②如图：把∠ABC放在∠DEF上，使点B和点E重合，边EF和BC重合，DE和BA在EF的同侧，从图形可以看出∠DEF能包含∠ABC，即∠DEF>∠ABC15(1)【答案】解：当∠DBA是锐角时，∠DBC是钝角，满足∠DBA<∠DBC(2)【答案】解：当∠DBA是钝角时，∠DBC是锐角，满足∠DBA>∠DBC(3)【答案】解：当∠DBA是直角时，∠DBA=∠DBC=90∘，满足∠DBA=∠DBC16.【答案】:D【解析】:∠ABC=30∘+90∘=120∘. 故选D17.【答案】:D【解析】:因为135∘=90∘+45∘，120∘=90∘+30∘，75∘=30∘+45∘，所以选项A，B，C的角均可画出，而25∘不能写成90∘，60∘，45∘，30∘的和或差，故画不出18.【答案】:A【解析】:利用36∘，45∘，72∘，90∘的和或差能得到：90∘−36∘=54∘，63∘=90∘−72∘+45∘，99∘=90∘+45∘−36∘，144∘=72∘+72∘，153∘=72∘+72∘+45∘−36∘，171∘=90∘+36∘+45∘，72∘角可以直接用含72∘角的三角板画出，一共能画出的角有7个19.【答案】:C20.【答案】:B【解析】:角α，β都是钝角，α，β都大于90∘且小于180∘，所以α+β的结果大于180∘且小于360∘，所以1(α+β)的结果大于30∘且小于60∘.显然只有选项B符合题意6。