福建省厦门一中09高三质检数学文

2009年福建省普通高中毕业班质量检查文科数学本试卷分第I 卷（选择题）和第Ⅱ卷（非选择题）， 本试卷共5页，满分150分，考试时间120分钟。

注意事项：1．答题前，考生先将自己的姓名、准考证号填写在答题卡上。

2．考生作答时，将答案答在答题卡上，请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效，在草稿纸、试题卷上答题无效。

3．选择题答案使用2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案标号；非选择题答案使用0.5毫米的黑色中性（签）笔或碳素笔书写，字体工整、笔记清楚。

4．做选考题时，考生按照题目要求作答，并用2B 铅笔在答题卡上把所选题目对应的题号涂黑。

5．保持答题卡卡面清洁，不折叠、不破损，考试结束后，将本试卷和答题卡一并交回。

参考公式：样本数据12,x x ，…，n x 的标准差 锥体体积公式s = 13V Sh =其中x -为样本平均数 其中S 为底面面积，h 为高 柱体体积公式 球的表面积、体积公式V Sh = 2344,3S R V R ππ==其中S 为底面面积，h 为高 其中R 为球的半径第I 卷（选择题 共60分）一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1.复数()()122i i -+等于( )A 43i -B 3i -C 34i -D 3i 2.已知全集{}1,2,3,4,U =，集合{}{}2,3,4,1,2P Q ==，则( ) A P Q Q = B ()U P Q Q =ð C PQ U = D ()U P Q P =ð 3．为了测算如图阴影部分的面积，作一个变长为6的正方形将其包含在内，并向正方形内随机投掷800个点，已知恰有200个点落在阴影部分内，据此，可估计阴影部分的面积是( )A 12B 9C 8D 6 4.函数()1f x Inx x=-的零点所在的区间是( ) A ()0,1 B ()1,e C (),3e D ()3,+∞5.如图所示，一个空间几何体的正视图和侧视图都是变长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的侧面积．．．为( )A 32πB 54πC πD 4π6 “1k =”是“直线0x y k -+=与圆221x y +=相交”的( ) A 充分而不必要条件 B 必要而不充分条件C 充分必要条件D 既不充分也不必要条件7.设向量a 与b 的夹角为θ，()()2,1,24,5a a b =+=则cos θ等于( )AB C 35 D 458.设,αβ为不重合的平面，,m n 为不重合的直线，则下列命题正确的是( ) A 若,,//,//m n m n αβαβ⊂⊂则 B 若,,,n n m m αββα⊂⊥⊥⊥则 C 若//,//,,m n m n αβαβ⊥⊥则 D 若,,,n m n m αββα⊥⊥⊥⊥则9.双曲线2221x y a-=过点()P ，则双曲线的焦点坐标是( )A )(),B )(),C ((,0,D ((,0,10已知0a，直线220a x y ++=与直线()2110bx a y -+-=互相垂直，则ab 的最小值( )A 4B 3C 3D 111.已知()f x '是函数()y f x =的导函数，且()y f x '=的图像如图所示，则()y f x =函数的图像可能是( )12.设M 是由平面内一些向量组成的集合，若对任意正实数和向量，都有，则称M 为锥，现有下列平面向量的集合：①(){}2,x y x y ≤ ②()20,30x y x y x y ⎧⎫-⎧⎪⎪⎨⎨⎬-⎩⎪⎪⎩⎭③(){}22,20x y xy - ④(){}22,340x y x y x+-上述为锥的集合的个数是( )A 1B 2C 3D 4第Ⅱ卷（非选择题 共100分）二、填空题：本大题共4小题，每小题4分，共16分，把答案填在答题卡相应位置。

福建省厦门一中2009届高三年质量检测数学（文科）一：选择题（12小题，每小题5分，共60分）1．在等差数列{}n a 中， 284a a +=,则 其前9项的和S9等于 A ．18 B 27 C 36 D 92函数()()sin cos sin f x x x x =-的最小正周期为 A4π B 2πC πD 2π 3．已知命题p: {}4A x x a=-,命题q :()(){}230B x x x =--,且⌝p 是⌝q 的充分条件，则实数 a 的取值范围是： A (-1,6) B[-1,6] C (,1)(6,)-∞-⋃+∞ D (,1][6,)-∞-⋃+∞4．用系统抽样法从160名学生中抽取容量为20的样本，将160名学生从1~160编号，按编号顺序平均分成20组（1~8号，9~16号，。

，153~160号）。

若第16组应抽出的号码为126，则第一组中用抽签方法确定的号码是 A 4 B 5 C 6 D 75．已知一个球与一个正三棱柱的三个侧面和两个底面相切，若这个球的体积是323π，则这个三棱柱的体积是A B6．在右图的程序框图中，改程序框图输出的结果是28，则序号①应填入的条件是A K>2B K>3C K>4D K>57．已知直线l 与圆C ： 221x y +=相切于第二象限，并且标轴所围城的三角形的面积为Ａ23 Ｂ12Ｃ１或３ Ｄ1322或８．设a β、是两个平面，l 、ｍ是两条直线，下列命题中，可以判断||a β的是 Ａ．,,||||l a m a l m ββ⊂⊂且， Ｂ．,,||l a m m ββ⊂⊂且 Ｃ．||a ||l m β，且l||m Ｄ．,,||l a m l m β⊥⊥且 ．９．若定义在Ｒ上的函数()f x 图像关于点（－34，０）成中心对称，对任意的实数x 都有3()()2f x f x =-+，且()11f -=，()02f =-，则 ）()()()()1232008f f f f +++⋅⋅⋅的值为A.-2B. -1C. 0D. 1 １０．函数 ()()log 310,1n y x a a =+-≠的图像恒过定点Ａ，若Ａ在直线ｍｘ＋ｎｙ＋１＝０上，其中ｍ、ｎ均为正数，则12m n+的最小值为 Ａ ２ Ｂ ４ Ｃ ６ Ｄ ８2|a|=2|b|0,x x ||0a x a b b ≠++⋅=已知且关于的方程有实根，则a 与的夹角的取值范围是Ａ[0,]6πＢ ［3π，π］ Ｃ 2[,]33ππ Ｄ[,]6ππ １２若函数()2,f x =对任意的1212,,23x x x x 且，那么有Ａ ()()1221x f x x f x Ｂ()()1221x f x x f x = Ｃ()()1221x f x x f x Ｄ()()1122x f x x f x =二．填空题（每小题４分，共１６分）１３ 在复平面内，复数１＋ｉ与－１＋３ｉ分别对应向量OA OB 和其中Ｏ为坐标原点，则｜AB ｜＝１４ 设等比例{}n a 的前ｎ项和为12161,,4n S SS S S =48且则＝ １５ 在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c，若)cos cos ,c A a C -=则 cosA=已知F1 F2是双曲线22221x y a b-=（a>0,b>0）的两个焦点，以线段F1 F2为边作正△M F1 F2，若边MF1的中点在双曲线上，则双曲线的离心率e=三．解答题（6大题，共74分）17.（12分）若函数()sin sin cos (0)f x x x x ωωωω=->的图像的任意两条对称轴之间的距离的最小值为2π，（1）当[0,]4x π∈时，求f(x)的减区间；（2）若将函数f(x)的图像向右平移φ（0<φ<2π）个单位后所得函数为g(x),若g(x)为偶函数，求φ18．（12分）设函数 ()3f x ax bx c =++是定义在R 上的奇函数，且函数()f x 的图像在x=1处的切线方程y=3x+2.（1）求函数()f x 的表达式；（2）若对任意x (0,1]∈都有 ()f x <mx成立，求实数m 的取值范围。

2009年福建省厦门市高三质量检查测试三数学(理科)试题本试卷分第I卷(选择题)和第n卷(非选择题)两部分.满分为150分，考试时间120分钟.注意事项:1.考生将自己的姓名、准考证号及所有答案均填写在答题卡上;2.答题要求，见答题卡上的填涂样例”和注意事项”.参考公式：如果事件A、B互斥，那么P (A+B) =P (A) +P ( B)如果事件A、B相互独立，那么P (AB) =P (A) P (B)如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k 次的概率P n(k)=C n k P k(1 -P)n-k2球的表面积公式：S=4nR,其中R表示球的半径.4 3球的体积公式：V=—nR其中R表示球的半径•3第I卷(选择题共60分)一、选择题：本大题共12个小题，每小题5分，在每小题给出的四个选项中，只有的•1.设集合A 二{y|y =x2,x R}, B 二{ y | y = 2x, x R},则A B 等于()项是符合题目要求A.{y|y 0}B. {2,4}C.{(2,4),(4,16)}D. {4,16}2下列函数中，值域是0,儿 3 ［的是( )w.w.w.k.s.5.u.c.o.mA. y =2x 1 (x 0)B. y = lg(x21)C. y=2D. y = . x2-2x-1x3.用反证法证明命题：“，b€ N,5整除"时，假设的内容应为( A.a, b都能被5整除C. a, b不都能被5整除4 .下列函数既是奇函数，又在区间A f (x)二sin x B. f (x) = - x 1 ab可被5整除，那么a, b中至少有一个能被 )B. a, b都不能被5整除D. a不能被5整除I "1,1上单调递减的是( )1』x 丄=i 2 —xC. f (x) a aD. f (x)二ln2 2 +x两个锐角，则下列不等式关系中正确的是A . f (sin _：J f (cos :)C. f (COS ： ) f(cos :)D. f (sin 二)：：f (cos :)一竺 生，若 |f(xJ-f(X 2)卜|f(：)-fC)|，则()1 ■A . ■ 0B . ' =0C. 0 ：：：'：：： 1D .— 111.某初级中学有学生 270人，其中一年级108人，二、三年级各 81人，现要利用抽样方法抽取10人参加某项调查，考虑选用简单随机抽样、分层抽样和系统抽样三种方案，使用简单随机抽样和分层抽样 时，将学生按一、二、三年级依次统一编号为 1, 2，…，270;使用系统抽样时，将学生统一随机编 号1 , 2,…，270,并将整个编号依次分为10段。

福建省厦门第一中学2024-2025学年度第一学期入学考高三年数学试卷满分：150分考试时间：120分钟一、单选题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.设集合{}{}2|e 1,|log (2)x P y y M x y x ==+==-，则集合M 与集合P 的关系是（）A.M P =B.P M∈ C.M P⊆ D.P M⊆2.设等差数列{}n a 的前n 项和为n S ，且公差不为0，若4a ，5a ，7a ，成等比数列，1166S =，则8a =（）A.7B.8C.10D.1233.已知偶函数2()1f x ax bx ++＝的定义域[a ﹣1，2]，则函数()f x 的值域为（）A.（﹣∞，1） B.（﹣∞，1]C.[﹣3，1]D.[1，+∞）4.已知3cos 5α=，3,22αππ⎛⎫∈ ⎪⎝⎭，则sin 2α=（）A.55 B.55-C.45D.2555.设函数()23a xf x -=在区间()1,2上单调递减，则a 的取值范围是（）A.(],2-∞ B.(],4∞- C.[)2,+∞ D.[)4,+∞6.四棱台的上底面是边长为2的正方形，下底面是边长为4的正方形，四条侧棱的长均为，则该四棱台的体积为（）A. B. C.2863D.7.已知函数()()()sin 0f x A x ωϕω=+>是偶函数，将()y f x =的图象向左平移π6个单位长度，再将图象上各点的横坐标变为原来的2倍（纵坐标不变），得到()y g x =的图象．若曲线()y g x =的两个相邻对称中心之间的距离为2π，则（）A.2ω=B.()g x 的图象关于直线π3x =对称C.()g x 的图象关于点2π,03⎛⎫⎪⎝⎭对称D.若()π2f =-，则()g x 在区间[]0,π8.已知函数()f x 、()g x 的定义域均为R ，函数()f x 的图象关于点()1,1--对称，函数+1的图象关于y 轴对称，()()211f x g x +++=-，()40f -=，则()()20302017f g -=（）A.4- B.3- C.3D.4二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的四个选项中，有多个选项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分．9.某社团开展“建党100周年主题活动——学党史知识竞赛”，甲、乙两人能得满分的概率分别为34，23，两人能否获得满分相互独立，则（）A.两人均获得满分的概率12B.两人至少一人获得满分的概率712C.两人恰好只有甲获得满分的概率14D.两人至多一人获得满分的概率1210.已知函数() cos sin f x x x x =-，则（）A.函数()f x 在2x π=时，取得极小值1-B.对于()0,x π∀∈，()0f x <恒成立C.若120x x π<<<，则1122sin sin x x x x <D.若sin x ab x<<，对于0,2x π⎛⎫∀∈ ⎪⎝⎭恒成立，则a 的最大值为2π，b 的最小值为111.已知曲线C 是平面内到定点()0,1F 和定直线l ：1y =-的距离之和等于4的点的轨迹，若()00,P x y 在曲线C 上，则（）A .曲线C 关于x 轴对称B.曲线CC.曲线C 及其内部共包含了19个整点（即横、纵坐标均为整数的点）D.点()00,P x y 到点31,2Q ⎛⎫- ⎪⎝⎭和点()0,1F 的距离之和最小为92三、填空题：本题共3小题，每小题5分，共15分．12.612x x ⎛⎫+- ⎪⎝⎭展开式中3x 的系数为__________.13.已知抛物线C ：y 2＝4x 的焦点为F ，A 为C 上一点，且|AF |＝5，O 为坐标原点，则OAF △的面积为___________.14.已知函数()()()sin 0f x x ωϕω=+>在ππ,36⎡⎤-⎢⎥⎣⎦上单调，π4ππ633f f f ⎛⎫⎛⎫⎛⎫==-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则ω的可能取值为______.四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15.在ABC V 中，内角A ，B ，C 的对边分别为a ，b ，c ，且22cos a c b C +=．（1）求B ；（2）若AC =，点D 是线段AC 上的一点，且ABD CBD ∠=∠，4BD =．求ABC V 的周长．16.如图，在四棱锥P ABCD -中，//BC AD ，1AB BC ==，3AD =,点E 在AD 上，且PE AD ⊥，2PE DE ==．（1）若F 为线段PE 中点，求证：//BF 平面PCD ．（2）若AB ⊥平面PAD ，求平面PAB 与平面PCD 夹角的余弦值．17.已知偶函数()f x 和奇函数()g x 均为幂函数，()ln h x kx =，且()()()()2332f g f g >.（1）若()()()u x f x g x =+，证明：102u ⎛⎫-> ⎪⎝⎭；（2）若()()()u x f x h x =-，()24f =，且()0u x ≥，求k 的取值范围；（3）若()()()u x g x h x =，()21f =，()ln e k g =，证明：()u x 在区间1,e⎛⎫+∞ ⎪⎝⎭单调递增.18.已知椭圆E ：()222210+=>>x y a b a b的离心率为22，A ，B 分别是E 的左、右顶点，P 是E 上异于A ，B 的点，APB △的面积的最大值为（1）求E 的方程；（2）设O 为原点，点N 在直线2x =上，N ，P 分别在x 轴的两侧，且APB △与NBP △的面积相等.（i ）求证：直线ON 与直线AP 的斜率之积为定值；（ⅱ）是否存在点P 使得APB NBP ≌△△，若存在，求出点P 的坐标，若不存在，说明理由.19.甲和乙两个箱子中各装有N 个大小、质地均相同的小球，并且各箱中35是红球，25是白球.（1）当5N =时，分别从甲、乙两箱中各依次随机地摸出3个球作为样本，设从甲箱中采用不放回摸球得到的样本中红球的个数为X ，从乙箱中采用有放回摸球得到的样本中红球的个数为Y ，求()E X ，()E Y ，()D X ，()D Y ；（2）当10N =时，采用不放回摸球从甲箱中随机地摸出5个球作为样本，设()12345k A k =，，，，表示“第k 次取出的是红球”，比较()1234P A A A A 与()()()()1234P A P A P A P A 的大小；（3）由概率学知识可知，当总量N 足够多而抽出的个体足够少时，超几何分布近似为二项分布.现从甲箱中不放回地取3个小球，恰有2个红球的概率记作1P ；从乙箱中有放回地取3个小球，恰有2个红球的概率记作2P .那么当N 至少为多少时，我们可以在误差不超过0.003（即120.003P P -≤)的前提下认为超几何分布近似为二项分布？（参考数据：17.03≈)福建省厦门第一中学2024-2025学年度第一学期入学考高三年数学试卷满分：150分考试时间：120分钟一、单选题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.设集合{}{}2|e 1,|log (2)x P y y M x y x ==+==-，则集合M 与集合P 的关系是（）A.M P =B.P M∈ C.M P⊆ D.P M⊆【答案】C 【解析】【分析】求出集合P 中函数的值域，集合Q 中函数的定义域，得到这两个集合，可判断集合间的关系.【详解】函数e 1x y =+值域为()1,+∞，函数2log (2)y x =-定义域为()2,+∞，即()1,=+∞P ，()2,M =+∞，所以有M P ⊆.故选：C.2.设等差数列{}n a 的前n 项和为n S ，且公差不为0，若4a ，5a ，7a ，成等比数列，1166S =，则8a =（）A.7B.8C.10D.123【答案】C 【解析】【分析】设公差为d ，由题意可得1,a d 的方程组，解方程组求出n a 可得答案.【详解】设公差为d ，由题意可得5547111101111662a a a a S a d ⨯=⨯⎧⎪⎨⨯=+=⎪⎩，即()()()21111436115566a d a d a d a d ⎧+=+⨯+⎪⎨+=⎪⎩，解得106d a =⎧⎨=⎩舍去，或124d a =⎧⎨=-⎩，所以()42126n a n n =-+-=-，可得816610=-=a .故选：C.3.已知偶函数2()1f x ax bx ++＝的定义域[a ﹣1，2]，则函数()f x 的值域为（）A.（﹣∞，1） B.（﹣∞，1]C.[﹣3，1]D.[1，+∞）【答案】C 【解析】【分析】根据偶函数的定义域特征，求出a 的值，再由偶函数的定义求出b ，结合二次函数图像，即可求解.【详解】已知偶函数2()1f x ax bx ++＝的定义域[]21a -，，所以12,1a a -=-∴=-，()(),f x f x x R -=∈恒成立，即2211,20,x bx x bx bx x R --+=-++=∈恒成立，20,()1,[2,2]b f x x x ∴=∴=-+∈-，函数()f x 的值域为[3,1]-.故选:C.【点睛】本题考查偶函数的性质，以及二次函数的性质，函数的奇偶性要注意定义域满足的条件，属于基础题.4.已知3cos 5α=，3,22αππ⎛⎫∈ ⎪⎝⎭，则sin 2α=（）A.55 B.55-C.45D.255【答案】A 【解析】【分析】由已知可求得3,24αππ⎛⎫∈ ⎪⎝⎭，进而sin 02α>，再根据余弦的二倍角公式进行计算即可得解.【详解】 3cos 5α=，3,22αππ⎛⎫∈ ⎪⎝⎭，∴3,24αππ⎛⎫∈ ⎪⎝⎭，则sin 02α>，23cos 12sin 25αα=-= ，可得21sin 25α=，5sin25α∴=．故选：A ．【点睛】易错点睛：本题容易忽略2α的取值范围，进而忽略sin 2α的范围，将结果求错.5.设函数()23a xf x -=在区间()1,2上单调递减，则a 的取值范围是（）A.(],2-∞ B.(],4∞- C.[)2,+∞ D.[)4,+∞【答案】D 【解析】【分析】根据题意，由复合函数的单调性，列出不等式，代入计算，即可得到结果.【详解】函数3x y =在R 上单调递增，而函数()23a xf x -=在区间()1,2上单调递减，所以2y x a =-在区间()1,2单调递减，所以22a≥，解得4a ≥．故选：D ．6.四棱台的上底面是边长为2的正方形，下底面是边长为4的正方形，四条侧棱的长均为，则该四棱台的体积为（）A. B. C.2863D.【答案】C 【解析】【分析】根据四棱台的性质，结合四棱台的体积公式进行求解即可.【详解】过1A E AC ⊥，由正四棱台的性质可知：1A E 是该正四棱台的高，因为四边形11ACC A 是等腰梯形，所以()111122AE A C AC =-==，由勾股定理可知：1A E ===所以该四棱台的体积为(2212864233⨯+=，故选：C7.已知函数()()()sin 0f x A x ωϕω=+>是偶函数，将()y f x =的图象向左平移π6个单位长度，再将图象上各点的横坐标变为原来的2倍（纵坐标不变），得到()y g x =的图象．若曲线()y g x =的两个相邻对称中心之间的距离为2π，则（）A.2ω=B.()g x 的图象关于直线π3x =对称C.()g x 的图象关于点2π,03⎛⎫⎪⎝⎭对称D.若()π2f =-，则()g x 在区间[]0,π【答案】C 【解析】【分析】首先利用三角函数的性质求出()f x 和()g x 的关系，根据对称点距离和周期关系即可判断A ；求出正弦型函数的对称轴和对称中心即可判断BC ；利用整体法即可求出()g x 的最值.【详解】由于函数()()()sin 0f x A x ωϕω=+>是偶函数，所以ππ+2k ϕ=()k ∈Z ，由于将()y f x =的图象向左平移π6个单位长度，再将图象上各点的横坐标变为原来的2倍（纵坐标不变），得到()y g x =的图象，则()1πsin 26g x A x ωωϕ⎛⎫=++⎪⎝⎭，对于A ，因为曲线()y g x =的两个相邻对称中心之间的距离为2π，故2π4π12T ω==，解得1ω=，故A 不正确；所以函数()πsin π2f x A x k ⎛⎫=++ ⎪⎝⎭，则()cos f x A x =或()cos f x A x =-，()1ππsin π262g x A x k ⎛⎫=+++ ⎪⎝⎭，则()1πcos 26g x A x ⎛⎫=+ ⎪⎝⎭或()1πcos 26g x A x ⎛⎫=-+ ⎪⎝⎭，对于B ，令1ππ26x k +=()k ∈Z ，解得π2π3x k =-，Z k ∈，令ππ2π33k -=，解得1Z 3k =∉，则()g x 的图象不关于直线π3x =对称，故B 错误；对于C,令1πππ+262x k +=()k ∈Z ，解得2π2π+3x k =，Z k ∈，所以当0k =时，所以()g x 的图象关于点2π,03⎛⎫⎪⎝⎭对称，故C 正确；对于D ，当()π2f =-时，2A =-或2A =，所以()1πcos 26g x A x ⎛⎫=+ ⎪⎝⎭或()1πcos 26g x A x ⎛⎫=-+ ⎪⎝⎭，当()1π2cos 26g x x ⎛⎫=-+⎪⎝⎭时，当[]0,πx ∈时，1ππ2π,2663x ⎡⎤+∈⎢⎥⎣⎦，所以()g x 在[]0,π上单调递增，故函数的最大值为(π)1g =；当()1π2cos 26g x x ⎛⎫=+⎪⎝⎭时，当[]0,πx ∈时，1ππ2π,2663x ⎡⎤+∈⎢⎥⎣⎦，所以()g x 在[]0,π上单调递减，故函数的最大值为(0)g =，故D 错误；故选：C.8.已知函数()f x 、()g x 的定义域均为R ，函数()f x 的图象关于点()1,1--对称，函数+1的图象关于y 轴对称，()()211f x g x +++=-，()40f -=，则()()20302017f g -=（）A.4-B.3- C.3D.4【答案】B 【解析】【分析】根据函数的对称性及奇偶性可得()(2)2f x f x +--=-，(1)(1)g x g x -+=+，再由已知条件可得()g x 的周期，将所求转化为关于()g x 的函数值后，利用周期及(1)1g =即可求解.【详解】由函数()f x 的图象关于点()1,1--对称，所以()(2)2f x f x +--=-，令4x =-，可得(4)(2)2f f -+=-，即(2)2f =-，由函数+1的图象关于y 轴对称，可知函数+1为偶函数，所以(1)(1)g x g x -+=+，由()()211f x g x +++=-，令0x =，可得(1)1(2)1g f =--=，由()()211f x g x +++=-，可得()(1)1f x g x +-=-，(2)(3)1f x g x --+--=-，两式相加可得2(1)(3)2g x g x -+-+--=-，即(1)(3)0g x g x -+--=，可得(5)(1)0g x g x -+-+=，由(1)(1)g x g x -+=+可得(5)(1)0g x g x -++=，即()(6)0g x g x ++=，故(6)()g x g x +=-，所以(12)(6)()g x g x g x +=-+=，即函数()g x 的周期12T =，由()(1)1f x g x +-=-可知(2030)1(2029)f g =--，所以()()203020171(2029)(2017)1(1)(1)12(1)3f g g g g g g -=---=---=--=-.故选：B【点睛】关键点点睛：根据中心对称及偶函数得出一般关系()(2)2f x f x +--=-，(1)(1)g x g x -+=+，再由()()211f x g x +++=-，利用消元思想，转化为关于()g x 的关系式是解题的第一关键，其次利用()g x 的关系式求出()g x 的周期是第二个关键点，求出周期后利用赋值求特殊函数值即可得解.二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的四个选项中，有多个选项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分．9.某社团开展“建党100周年主题活动——学党史知识竞赛”，甲、乙两人能得满分的概率分别为34，23，两人能否获得满分相互独立，则（）A.两人均获得满分的概率12B.两人至少一人获得满分的概率712C.两人恰好只有甲获得满分的概率14D.两人至多一人获得满分的概率12【答案】ACD【解析】【分析】利用独立事件的概率乘法公式和对立事件的概率公式逐一求解即得.【详解】设A =“甲获得满分”，B =“乙获得满分”，则32(),()43P A P B ==,对于A ，“两人均获得满分”可表示为A B ⋂,因两人能否获得满分相互独立，故321()()()432P A B P A P B ⋂===,即A 正确；对于B ，因“两人至少一人获得满分”的对立事件为A B ⋂=“两人都没获得满分”,则“两人至少一人获得满分”的概率为：11111()1()()14312P A B P A P B -⋂=-=-⨯=，故B 错误；对于C ，“两人恰好只有甲获得满分”可表示为A B ⋂，其概率为：311()()()434P A B P A P B ⋂==⨯=，故C 正确；对于D ，因“两人至多一人获得满分”的对立事件为A B = “两人都获得满分”，则“两人至多一人获得满分”为：3211()1()()1432P A B P A P B -⋂=-=-⨯=,故D 正确.故选：ACD .10.已知函数() cos sin f x x x x =-，则（）A.函数()f x 在2x π=时，取得极小值1-B.对于()0,x π∀∈，()0f x <恒成立C.若120x x π<<<，则1122sin sin x x x x <D.若sin x ab x<<，对于0,2x π⎛⎫∀∈ ⎪⎝⎭恒成立，则a 的最大值为2π，b 的最小值为1【答案】BCD 【解析】【分析】利用导数研究()f x 在(0,)π上单调性及最值即可判断A 、B 的正误；构造sin ()xg x x=，应用导数研究单调性即知C 的正误；构造()sin h x x mx =-，应用导数并结合分类讨论的方法研究0,2x π⎛⎫∈ ⎪⎝⎭上()0h x >、()0h x <恒成立时m 的取值范围，即可判断正误.【详解】对AB ，()sin f x x x '=-，∴(0,)π上()0f x '<，即(0,)π上()f x 单调递减，则()(0)0f x f <=，∴A 错误，B 正确；对C ，令sin ()xg x x=，则在(0,)π上2cos sin ()0x x x g x x -'=≤，即()g x 单调递减，∴120x x π<<<时，有1212sin sin x x x x >，即1122sin sin x x x x <，C 正确；对D ，0x >，则sin x a x<等价于sin 0x ax ->，sin xb x <等价于sin 0x bx -<，令()sin h x x mx =-，则()cos h x x m '=-，0,2x π⎛⎫∈ ⎪⎝⎭，∴当0m ≤时，()0h x '>，则()h x 单调递增，故()(0)0h x h >=；当1m ≥时，()0h x '<，则()h x 单调递减，故()(0)0h x h <=；当01m <<时，存在00,2x π⎛⎫∈ ⎪⎝⎭使00()cos 0h x x m '=-=，∴此时，0(0,)x 上()0h x '>，则()h x 单调递增，()(0)0h x h >=；0(,)2x π上()0h x '<，则()h x 单调递减，∴要使()sin 0h x x mx =->在0(,2x π上恒成立，则(1022m h ππ=-≥，得20m π<≤.综上，2m π≤时，0,2x π⎛⎫∈ ⎪⎝⎭上()0h x >恒成立，1m ≥时0,2x π⎛⎫∈ ⎪⎝⎭上()0h x <恒成立，∴若sin x ab x<<，对于0,2x π⎛⎫∀∈ ⎪⎝⎭恒成立，则a 的最大值为2π，b 的最小值为1，正确.故选：BCD【点睛】关键点点睛：选项D ，由题设不等式构造()sin h x x mx =-，综合应用分类讨论、导数研究恒成立对应的参数范围，进而判断不等式中参数的最值.11.已知曲线C 是平面内到定点()0,1F 和定直线l ：1y =-的距离之和等于4的点的轨迹，若()00,P x y 在曲线C 上，则（）A.曲线C 关于x 轴对称B.曲线CC.曲线C 及其内部共包含了19个整点（即横、纵坐标均为整数的点）D.点()00,P x y 到点31,2Q ⎛⎫- ⎪⎝⎭和点()0,1F 的距离之和最小为92【答案】BC 【解析】【分析】由题意得到曲线C 的解析式，画出图象，由图直观判断即可.【详解】设(,)M x y 是曲线C 上任意一点，由于(,)M x y 到定点0,1和定直线:1l y =-的距离之和等于4.14y ++=，当1y ≥-3y =-，即222(1)69x y y y +-=-+，化简得：212(12)4y x y =--≤≤，当1y <-5y =+，化简得：212(21)12y x y =--≤≤-.画出曲线C 的图象：如图，对于A ，显然图象不关于x 轴对称，故A 错误；对于B ，212(12)4y x y =--≤≤，当1y =-时，解得1)-A ，点A =，故B 正确；对于C ，由A 可得[]2,2y ∈-，当2y =时，0x =，此时直线2y =在曲线上或内部有1个整点；当1y =时，2x =±，此时直线1y =在曲线上或内部有5个整点；当0y =时，x =±0y =在曲线上或内部有5个整点；当1y =-时，x =±1y =-在曲线上或内部有7个整点；当2y =-时，0x =，此时直线2y =-在曲线上或内部有1个整点；故曲线C 及其内部共包含了19个整点，故C 正确；对于D ，如图：点G 到0,1与到直线:1l y =-的距离之和为4，点00(,)P x y 到点31,2Q ⎛⎫- ⎪⎝⎭和点0,1的距离之和最小值为：44QG -<，故D 错误.故选：BC.【点睛】关键点点睛：本题解决的关键在于，根据题意，利用两点距离公式与点线距离公式得到曲线C 的解析式，从而作图即可得解.三、填空题：本题共3小题，每小题5分，共15分．12.612x x ⎛⎫+- ⎪⎝⎭展开式中3x 的系数为__________.【答案】220-【解析】【分析】将61(2)x x+-看作6个1(2)x x +-相乘，结合组合的知识即可直接求得答案.【详解】由题可得含3x 的项为()()13133344113636211C C 2C C C 2220x x x x ⎛⎫-+-=- ⎪⎝⎭，故答案为：220-.13.已知抛物线C ：y 2＝4x 的焦点为F ，A 为C 上一点，且|AF |＝5，O 为坐标原点，则OAF △的面积为___________.【答案】2【解析】【分析】根据抛物线的标准方程求出交点，再利用焦半径公式求出点A 的纵坐标，利用三角形的面积公式即可求解.【详解】根据题意，抛物线C ：24y x =的焦点为()10F ,，设(),A m n ，则+1=5AF m =，∴4m =，∴4n =±，∴11422AOF S =⨯⨯= .故答案为：214.已知函数()()()sin 0f x x ωϕω=+>在ππ,36⎡⎤-⎢⎥⎣⎦上单调，π4ππ633f f f ⎛⎫⎛⎫⎛⎫==-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则ω的可能取值为______.【答案】1239,,755【解析】【分析】根据函数的单调区间确定02ω<≤，再根据π4ππ633f f f ⎛⎫⎛⎫⎛⎫==-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭确定关于周期的相应等式，结合其范围，即可求得答案.【详解】设()()()sin 0f x x ωϕω=+>的周期为T ，函数()f x 在ππ,36⎡⎤-⎢⎥⎣⎦上单调，故2πππ2()π,0263T ωω⎡⎤=≥--=∴<≤⎢⎥⎣⎦；由ππ63f f ⎛⎫⎛⎫=-- ⎪ ⎪⎝⎭⎝⎭以及函数()f x 在ππ,36⎡⎤-⎢⎥⎣⎦上单调，得πππ630212f f ⎡⎤⎛⎫+- ⎪⎢⎥⎛⎫⎝⎭⎢⎥=-= ⎪⎝⎭⎢⎥⎢⎥⎣⎦，由π4π63f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，4ππ7π,π366T -=≥，得7π6T =或π4ππ632124T +=-+或π4ππ3632124T +=-+，若7π6T =，则7π2π12,67ωω=∴=；若π4ππ632124T +=-+，则3πππ,412253ωω=-+∴=；若π4ππ3632124T +=-+，则3ππ3π9,41225ωω=-+∴=；故ω的可能取值为1259,,735，故答案为：1239,,755四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15.在ABC V 中，内角A ，B ，C 的对边分别为a ，b ，c ，且22cos a c b C +=．（1）求B ；（2）若AC =，点D 是线段AC 上的一点，且ABD CBD ∠=∠，4BD =．求ABC V 的周长．【答案】（1）2π3（2）18+【解析】【分析】（1）利用正弦定理与和角公式，由题设得到1cos 2B =-，结合内角范围即得；（2）由等面积和余弦定理联立,求出18a c +=即得三角形的周长.【小问1详解】由22cos a c b C +=和正弦定理，2sin sin 2sin cos A C B C +=(*)，因sin sin()sin cos cos sin A B C B C B C =+=+,代入(*)化简得，2cos sin sin 0B C C +=,即sin (2cos 1)0C B +=，因sin 0C >，故得1cos 2B =-，因0πB <<,则2π3B =.【小问2详解】由题意知，BD 是ABC ∠的平分线.由ABC ABD BCD S S S =+△△△可得，2π1π()4sin 3231sin2a c ac =+⨯，化简得，4()c c a a =+①又由余弦定理，2222π2cos 3a c ac +-=，即2()252a c ac +-=②，将①代入②可得，2()4()2520a c a c +-+-=，解得18a c +=，（14a c +=-舍去），故ABC V 的周长为18+.16.如图，在四棱锥P ABCD -中，//BC AD ，1AB BC ==，3AD =,点E 在AD 上，且PE AD ⊥，2PE DE ==．（1）若F 为线段PE 中点，求证：//BF 平面PCD ．（2）若AB ⊥平面PAD ，求平面PAB 与平面PCD 夹角的余弦值．【答案】（1）证明见解析（2）3030【解析】【分析】（1）取PD 的中点为S ，接,SF SC ，可证四边形SFBC 为平行四边形，由线面平行的判定定理可得//BF 平面PCD .（2）建立如图所示的空间直角坐标系，求出平面APB 和平面PCD 的法向量后可求夹角的余弦值.【小问1详解】取PD 的中点为S ，接,SF SC ，则1//,12SF ED SF ED ==，而//,2ED BC ED BC =，故//,SF BC SF BC =，故四边形SFBC 为平行四边形，故//BF SC ，而BF ⊄平面PCD ，SC ⊂平面PCD ，所以//BF 平面PCD .【小问2详解】因为2ED =，故1AE =，故//,=AE BC AE BC ，故四边形AECB 为平行四边形，故//CE AB ，所以CE ⊥平面PAD ，而,PE ED ⊂平面PAD ，故,CE PE CE ED ⊥⊥，而PE ED ⊥，故建立如图所示的空间直角坐标系，则()()()()()0,1,0,1,1,0,1,0,0,0,2,0,0,0,2A B C D P --，则()()()()0,1,2,1,1,2,1,0,2,0,2,2,PA PB PC PD =--=--=-=-设平面PAB 的法向量为(),,m x y z =，则由0m PA m PB ⎧⋅=⎪⎨⋅=⎪⎩可得2020y z x y z --=⎧⎨--=⎩，取()0,2,1m =- ，设平面PCD 的法向量为(),,n a b c =，则由0n PC n PD ⎧⋅=⎪⎨⋅=⎪⎩可得20220a b b c -=⎧⎨-=⎩，取()2,1,1n = ，故30cos ,30m n ==-，故平面PAB 与平面PCD夹角的余弦值为3017.已知偶函数()f x 和奇函数()g x 均为幂函数，()ln h x kx =，且()()()()2332f g f g >.（1）若()()()u x f x g x =+，证明：102u ⎛⎫-> ⎪⎝⎭；（2）若()()()u x f x h x =-，()24f =，且()0u x ≥，求k 的取值范围；（3）若()()()u x g x h x =，()21f =，()ln e k g =，证明：()u x 在区间1,e⎛⎫+∞ ⎪⎝⎭单调递增.【答案】（1）证明见解析（2）)(k ⎡∈⎣ （3）证明见解析【解析】【分析】（1）根据幂函数解析式及性质可设函数解析式，再根据指数函数的单调性可证明不等式；（2）分情况讨论当0k >和0k <时函数的单调性与最值情况，进而可得解；（3）由已知可得0b a >=，求导，可转化为证明ln ln 10b b b x ++>在1,e⎛⎫+∞ ⎪⎝⎭恒成立，结合函数()ln 1F b b b b =-+的单调性与正负情况可得证.【小问1详解】由已知偶函数()f x 和奇函数()g x 均为幂函数，可设()af x x =和()bg x x =，且()()f x f x -=，()()g x g x -=-，又()()()()2332f g f g >，即2332a b a b ⋅>⋅，即2233a b⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭，又函数23xy ⎛⎫= ⎪⎝⎭单调递减，所以a b <，所以11111112222222a bu f g f g ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-=-+-=-=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，又函数12xy ⎛⎫= ⎪⎝⎭单调递减，所以1122ab⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭，即1110222abu ⎛⎫⎛⎫⎛⎫-=-> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭；【小问2详解】由已知()224a f ==，得2a =，即()2f x x =，所以()()()2ln u x f x h x x kx =-=-，当0k >时，()2ln u x x kx =-的定义域为()0,∞+，()21212x u x x x x -'=-=，令()0u x '=，解得2x =或22x =-（舍），所以当20,2x ⎛⎫∈ ⎪ ⎪⎝⎭时，()0u x '<，()u x 单调递减，当2,2x ⎛⎫∈+∞ ⎪ ⎪⎝⎭时，()0u x '>，()u x 单调递增，所以()212ln 0222u x u k ⎛⎫≥=-≥ ⎪ ⎪⎝⎭，解得k ≤(k ∈；当0k <时，()2ln u x x kx =-的定义域为(),0-∞，()21212x u x x x x -'=-=，令()0u x '=，解得2x =（舍）或22x =-，所以当2,02x ⎛⎫∈- ⎪⎝⎭时，()0u x '>，()u x 单调递增，当,2x ⎛⎫∈-∞ ⎪ ⎪⎝⎭时，()0u x '<，()u x 单调递减，所以()1ln 0222u x u k ⎛⎫⎛⎫≥-=--≥ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭，解得k ≥)k ⎡∈⎣；综上所述)(k ⎡∈⎣ 【小问3详解】由()ln e ln e bk g b ===，又已知()221af ==，所以0a =，由（1）得a b <，即0b >，所以函数()()()ln bu x g x h x x bx ==的定义域为()0,∞+，所以()()11ln ln 1b b b bu x bxbx x x b bx bx--'=+⋅=+，又10b x ->恒成立，且当1,ex ⎛⎫∈+∞ ⎪⎝⎭，所以ln 1x >-，ln 1ln ln 1ln 1b bx b b b x b b b +=++>-+，设()ln 1F b b b b =-+，则()ln 11ln F b b b '=+-=，令()0F b '=，则1b =，所以当()0,1b ∈时，()0F b '<，()F b 单调递减，当()1,b ∈+∞时，()0F b '>，()F b 单调递增，所以()()10F b F ≥=，所以ln 10b bx +>，即当1,ex ⎛⎫∈+∞ ⎪⎝⎭，()()1ln 10b u x xb bx -'=+>，所以函数()u x 在1,e⎛⎫+∞ ⎪⎝⎭上单调递增.【点睛】导数是研究函数的单调性、极值(最值)最有效的工具，而函数是高中数学中重要的知识点，对导数的应用的考查主要从以下几个角度进行：(1)考查导数的几何意义，往往与解析几何、微积分相联系．(2)利用导数求函数的单调区间，判断单调性；已知单调性，求参数．(3)利用导数求函数的最值(极值)，解决生活中的优化问题．(4)考查数形结合思想的应用．18.已知椭圆E ：()222210+=>>x y a b a b的离心率为22，A ，B 分别是E 的左、右顶点，P 是E 上异于A ，B 的点，APB △的面积的最大值为（1）求E 的方程；（2）设O 为原点，点N 在直线2x =上，N ，P 分别在x 轴的两侧，且APB △与NBP △的面积相等.（i ）求证：直线ON 与直线AP 的斜率之积为定值；（ⅱ）是否存在点P 使得APB NBP ≌△△，若存在，求出点P 的坐标，若不存在，说明理由.【答案】（1）22142x y +=（2）（ⅰ）证明见解析；（ⅱ）不存在点P 【解析】【分析】（1）利用待定系数法，列方程组，即可求解；（2）（ⅰ）首先利用坐标表示APB S 和NBP S ，利用面积相等，以及点P 在椭圆上的条件，即可化简斜率乘积的公式，即可证明；（ⅱ）由条件APB NBP ≌△△，确定边长和角度的关系，再结合数形结合，即可判断是否存在点P 满足条件.【小问1详解】当点P 是短轴端点时，APB △的面积最大，面积的最大值为122a b ⋅⋅=，则2222c a ab c a b ⎧=⎪⎪⎪=⎨⎪=-⎪⎪⎩，得222b c ==，24a =，所以椭圆E 的方程为22142x y +=；【小问2详解】（ⅰ）设0,0，()2,N t ，00ty <00122APB S AB y y =⨯⨯= ，()0122NPB S t x =⨯- ，由题意可知，()001222y t x =⨯-，0042y t x =-，即0042y t x -=-，所以20020021224AP ONy y t k k x x -=⨯==-+-；（ⅱ）假设存在点P ，使得APB NBP ≅ ，因为AB AP >，NP NB >，BP BP =，所以AP NB =，APB NBP ∠=∠，ABP NPB ∠=∠，则90APN NBA ∠=∠= ，由（ⅰ）可知，AP ON ⊥，又AP NP ⊥，所以,,O N P 三点共线，如图，则OPB OBP ∠=∠，所以2OP OB ==，则点P 与点A 重合，这与已知矛盾，所以不存在点P ，使APB NBP ≌△△.19.甲和乙两个箱子中各装有N 个大小、质地均相同的小球，并且各箱中35是红球，25是白球.（1）当5N =时，分别从甲、乙两箱中各依次随机地摸出3个球作为样本，设从甲箱中采用不放回摸球得到的样本中红球的个数为X ，从乙箱中采用有放回摸球得到的样本中红球的个数为Y ，求()E X ，()E Y ，()D X ，()D Y ；（2）当10N =时，采用不放回摸球从甲箱中随机地摸出5个球作为样本，设()12345k A k =，，，，表示“第k 次取出的是红球”，比较()1234P A A A A 与()()()()1234P A P A P A P A 的大小；（3）由概率学知识可知，当总量N 足够多而抽出的个体足够少时，超几何分布近似为二项分布.现从甲箱中不放回地取3个小球，恰有2个红球的概率记作1P ；从乙箱中有放回地取3个小球，恰有2个红球的概率记作2P .那么当N 至少为多少时，我们可以在误差不超过0.003（即120.003P P -≤)的前提下认为超几何分布近似为二项分布？（参考数据：17.03≈)【答案】（1）()E X =95，9()25D X =，918()()525E Y D Y ==（2）()()()()()12341234P A A A A P A P A P A P A <（3）195【解析】【分析】（1）由题意可得3~(3,)5Y B ，利用二项分布的期望公式和方差公式求解，X 服从超几何分布，X 的可能取值为1，2，3，求出相应的概率，从而可求出()E X 和()D X ；（2）利用独立事件概率公式和古典概率公式求出()1234P A A A A ，()()()()1234P A P A P A P A ，进行比较即可；（3）根据题意表示出12,P P ，由120.003P P -≤化简得21952900N N -+≥，解法1：转化为290195N N+≥，构造函数()()2900f x x x x=+>，利用函数的单调性求解；解法2：直接解一元二次不等式即可.【小问1详解】对于有放回摸球，每次摸到红球的概率为0.6，且每次试验之间的结果是独立的，则3393218~(3,),()3,()35555525Y B E Y D Y =⨯==⨯=X 服从超几何分布，X 的可能取值为1，2，3，则2112323233333555C C 3C C 3C 1(1)(2),(3)C 10C 5C 10P X P X P X =========3319()123105105E X ∴=⨯+⨯+⨯=，2229393919()1235105551025D X ⎛⎫⎛⎫⎛⎫=-⨯+-⨯+-⨯=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，或222233199()12310510525D X ⎛⎫=⨯+⨯+⨯-=⎪⎝⎭；【小问2详解】495106A 3()A 5k P A ⨯==Q ，即采用不放回摸球，每次取到红球的概率都为()35k P A =：41234381()()()()5625P A P A P A P A ⎛⎫∴==⎪⎝⎭又()14661234510A C 65436181A 10987635625P A A A A ⨯⨯⨯⨯===<⨯⨯⨯⨯，则()()()()()12341234P A A A A P A P A P A P A <.【小问3详解】因为()22233254C 0.43255125P =⨯=⎪=⎛⎫ ⎝⎭，()()213235133313255C C 11852512C 25(1)(2)6NNNN N N N N P N N N N N ⎛⎫- ⎪⎛⎫⎝⎭-⋅ ⎪⎝⎭===⨯----，120.003P P -≤Q ，即311850.4320.00325(1)(2)N N N N ⎛⎫- ⎪⎝⎭⨯-≤--，即311850.43525(1)(2)N N N N ⎛⎫- ⎪⎝⎭⨯≤--，即31295(1)(2)48N N N N ⎛⎫- ⎪⎝⎭≤--，由题意知()()120N N -->，从而()()348129125N N N N ⎛⎫-≤ ⎪⎝⎭--，化简得21952900N N -+≥，解法1：又0N >，290195N N ∴+≥，令()()2900f x x x x=+>，则()2222902901x f x x x-'=-=，所以当0x <<()0f x '<，当x >时()0f x '>，所以()f x 在(上单调递减，在)+∞上单调递增，(此处证单调性另解：()()2900f x x x x=+>为对勾函数，()29034.06f x xx=+≥≈，（当且仅当x =时取等）.所以()f x 在(上单调递减，在)+∞上单调递增)，所以()f x 在17.03x =≈处取得最小值，从而290y N N=+在18N ≥时单调递增，当20N ≤时，290147N N+<，又290193194.50195193+≈<，290194195.49195194+≈>，∴当194N ≥时，符合题意考虑到25N ，35N 都是整数，则N 一定是5的正整数倍，所以N 至少为195时，在误差不超过0.003（即120.003P P -≤）的前提下认为超几何分布近似为二项分布.解法2：化简得21952900N N -+≥，1952N <或1952+，N 为整数，1N ∴≤或194N ≥25N Q，35N 都是整数，则N 一定是5的正整数倍，所以N 至少为195时，在误差不超过0.003（即120.003P P -≤）的前提下认为超几何分布近似为二项分布.【点睛】关键点点睛：此题解题的关键是根据题意正确区分二项分布和超几何分布，利用二项分布和超几何分布的概率公式求解，从而得解.。

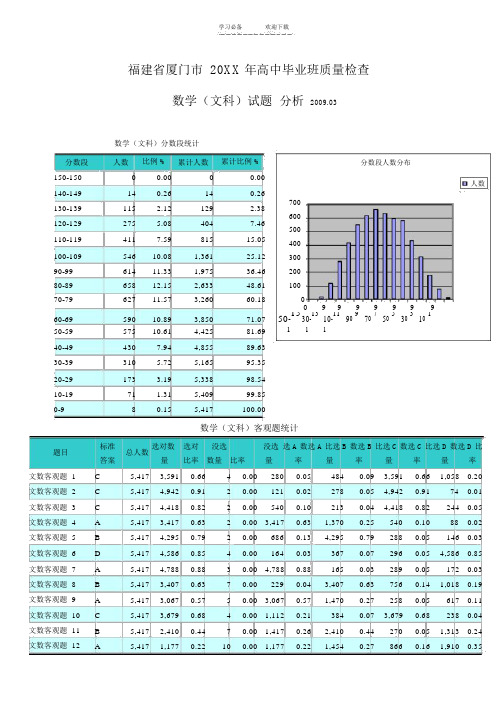
学习必备 欢迎下载福建省厦门市 20XX 年高中毕业班质量检查数学（文科）试题 分析 2009.03数学（文科）分数段统计分数段人数比例 %累计人数累计比例 %分数段人数分布150-150 0 0.00 0 0.00人数140-149 14 0.26 14 0.26700 130-139 115 2.12 129 2.38600120-129 275 5.08 404 7.46500110-1194117.5981515.05400100-109 546 10.08 1,361 25.12 300 90-99 614 11.33 1,975 36.46 200 80-89 658 12.15 2,633 48.61 10070-7962711.573,26060.18 00 9 99999960-69 590 10.89 3,850 71.07 50-1530-1310-1190-970-750-530-310-150-59 575 10.61 4,425 81.6911 140-49 430 7.94 4,855 89.63 30-39 310 5.72 5,165 95.35 20-29 173 3.19 5,338 98.54 10-19 71 1.31 5,409 99.85 0-980.155,417100.00数学（文科）客观题统计题目标准 总人数 选对数 选对没选 没选 选A 数选A 比选B 数选 B 比选C 数选C 比选D 数选D 比答案 量 比率 数量 比率 量 率 量 率 量 率 量 率文数客观题 1 C 5,417 3,591 0.66 4 0.00 280 0.05 484 0.09 3,591 0.66 1,058 0.20文数客观题 2 C 5,417 4,942 0.91 2 0.00 121 0.02 278 0.05 4,942 0.91 74 0.01文数客观题 3 C 5,417 4,418 0.82 2 0.005400.10 213 0.04 4,418 0.82 244 0.05文数客观题 4 A 5,417 3,417 0.63 2 0.00 3,417 0.63 1,370 0.25 540 0.10 88 0.02文数客观题 5 B 5,417 4,295 0.79 2 0.00 686 0.13 4,295 0.79 288 0.05 146 0.03文数客观题 6 D 5,417 4,586 0.85 4 0.001640.03 367 0.07 296 0.05 4,586 0.85文数客观题 7 A 5,417 4,788 0.88 3 0.00 4,788 0.88 165 0.03 289 0.05 172 0.03文数客观题 8 B 5,417 3,407 0.63 7 0.002290.04 3,407 0.63 756 0.14 1,018 0.19文数客观题 9 A 5,417 3,067 0.57 5 0.00 3,067 0.57 1,470 0.27 258 0.05 617 0.11文数客观题 10 C 5,417 3,679 0.68 4 0.00 1,112 0.21 384 0.07 3,679 0.68 238 0.04文数客观题 11 B 5,417 2,410 0.44 7 0.00 1,417 0.26 2,410 0.44 270 0.05 1,313 0.24文数客观题 12A5,4171,1770.22100.00 1,1770.221,4540.278660.161,910 0.35数学（文科）分题质量统计题目满分总人数及格人及格率优秀人优秀平均分最高分标准差难度区分度数数率文数客观题 1 5.005,4173,5910.663,5910.66 3.31 5.00 2.360.660.31文数客观题 2 5.005,4174,9420.914,9420.91 4.56 5.00 1.410.910.39文数客观题 3 5.005,4174,4180.824,4180.82 4.08 5.00 1.940.820.45文数客观题 4 5.005,4173,4170.633,4170.63 3.15 5.00 2.410.630.51文数客观题 5 5.005,4174,2950.794,2950.79 3.96 5.00 2.030.790.45文数客观题 6 5.005,4174,5860.854,5860.85 4.23 5.00 1.800.850.45文数客观题 7 5.005,4174,7880.884,7880.88 4.42 5.00 1.600.880.41文数客观题 8 5.005,4173,4070.633,4070.63 3.14 5.00 2.420.630.50文数客观题 9 5.005,4173,0670.573,0670.57 2.83 5.00 2.480.570.38文数客观题 10 5.005,4173,6790.683,6790.68 3.40 5.00 2.330.680.31文数客观题 11 5.005,4172,4100.442,4100.44 2.22 5.00 2.490.440.40文数客观题 12 5.005,4171,1770.221,1770.22 1.09 5.00 2.060.220.11文数第 13题 4.005,4174,5500.844,5500.84 3.36 4.00 1.470.840.33文数第 14题 4.005,4172,7860.512,7860.51 2.06 4.00 2.000.510.60文数第 15题 4.005,4171,0800.201,0800.200.80 4.00 1.600.200.51文数第 16题 4.005,4171,1320.211,1320.210.84 4.00 1.630.210.45文数第 17(1)题 6.005,4173,0430.562,9840.55 3.55 6.00 2.780.590.71文数第 17(2)题 6.005,4172,1780.401,7490.32 2.44 6.00 2.640.410.73文数第 18(1)题 4.005,4175,1730.955,0810.94 3.80 4.000.780.950.28文数第 18(2)题8.005,4173,3150.613,1150.58 4.928.00 3.420.610.53文数第 19(1)题 5.005,4174,1120.763,9800.73 3.71 5.00 1.930.740.61文数第 19(2)题7.005,4172,2190.411,8230.34 3.407.00 2.840.490.74文数第 20(1)题 6.005,4171,9430.369390.17 2.11 6.00 2.180.350.66文数第 20(2)题 6.005,4179370.178220.15 1.17 6.00 2.170.190.62文数第 21(1)题 4.005,4173,4590.643,3950.63 2.70 4.00 1.730.680.67文数第 21(2)题8.005,4171650.03880.020.648.00 1.370.080.58文数第 22(1)题 3.005,4172,4860.462,4150.45 1.58 3.00 1.330.530.71文数第 22(2)题 5.005,4172360.041620.030.36 5.000.970.070.46文数第 22(3)题 6.005,41750.0010.000.04 5.500.290.010.2560.005,4173,4490.641,6350.3040.4160.0011.430.670.0090.005,4171,2630.232070.0437.4885.0019.510.420.00150.005,4171,9750.364040.0777.89145.0028.560.520.00填空题：（题组长：厦门六中杜幼兰）第 13 题考查：会读懂程序框图，会执行框图所表示的算法步骤，推测算法的执行结果。

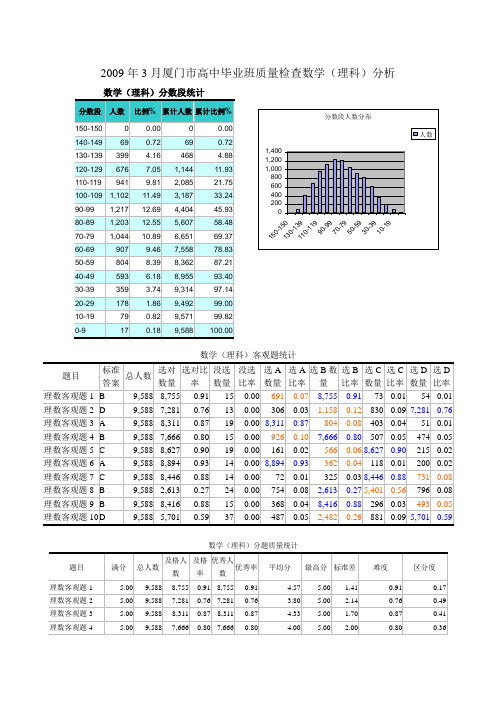
2009年3月厦门市高中毕业班质量检查数学（理科）分析数学（理科）客观题统计数学（理科）分题质量统计数学（理科）分数段统计填空题：（题组长：禾山中学 周卓）1. 11题不容易出情况，得分率应该是最高的。

2. 本小题是要写出渐近线方程，标准答案是03=±y x 。

学生出现了x y 3±=，y x 33±=，0322=±y x 这几种正确形式，还有x y 212±=等没化简的。

最多出现漏写x 的情况（3±=y ），以及漏写正负号的情况（x y 3=）；还有3±=xy；写成平方式的：012422=+y x 、012422=-y x ；还有1322=±yx 的这几种错误。

3. 13题很多0.32，0.64的答案。

4. 14题标准答案是64，有学生写成62，也正确。

但是有写成n2，没有求出n 来。

5. 15题有学生没省清题意直接写2。

需要的是比分2：0。

第16题：（题组长：湖滨中学 李明 科技中学 钟旗法）本题主要考查函数零点的概念，三角函数性质、三角恒等变换等基本知识，考查推理和运算能力.其他解法：（许多同学书写的不够完整）由())1f x x π=--,列表如下：∴max ()1.8f x x ==时， 另有学生通过作图由图像获得答案。

存在的主要问题： 1． 求得())4f x x π=-，漏掉-1, 也有不少同学漏掉了2；2．由()2sin cos cos 21f x x x x =--直接得T π=，缺乏理由； 3． 值域中只求了当38x π=1，忘了求值域；4． 没求22,()2cos 2)5a f x x x T aπ=+=直接得. 5． 解题格式不够规范，甚至出现只有答案，没有过程的现象；6． 审题不认真，有部分学生用求导的方法求得a ，把“零点”看做或理解为“极值点”； 7． 公式sin cos )a x b x x ϕ+=+有一部分同学运用不够熟练，出现符号错误，丢失大量的分值；8． 解题过程中的组织能力不强，许多同学出现漏答的情况，即最后没有“点题”。

勒罗的眼泪是演员进入角色后的 真实感情的流露。

课文中勒罗说他是在演戏，并且说“没有感情演不成戏”。

演员也常常说这么一名话“不进入角色，出不来”在送行过程中，勒罗已经把自己当成美国小姐的父亲或她的亲朋好友来表演，由于“他是优秀演员”，他进入美国小姐父亲的角色，他想到女儿即将离自己，非常担忧女儿在外的日子，于是反复叮， 提出旅途中的最好的忠告，并且恋恋不舍，于是不由自主地流下了惜别的泪水当然，这不是现实中勒罗的惜别之泪，而是表演“月台父女送别”这一出戏中的父亲这个角色对戏中女儿的惜别之泪，可以把这种泪水叫做：戏中父亲的角色之泪。

作者作为漫画家，从看似幽默滑稽的语言中体味到对生活深刻思考和哲理。

这正是这篇幽默散文所具有的喜剧效果。

分角色表演第六自然段，感受作者“不动声色”的幽默手法把尴尬写的惟妙惟肖，这也是文章产生了喜剧效果。

真正送行者反而尴尬，扮演送行者却动真情。

可见真的东西不一定有价值，假的东西不一定没有价值。

（联系我们的生活经历和感受谈一谈你对这句话的理解。

） 学习一篇课文，不仅要领会课文的内容，而且要掌握积累所学课文中词句，为今后的读写打基础，下面请同学们再读课文，划出文中的关键词语，然后全班交流。

注意词不离句，句不离文。

捕捉文章对罗勒的细节描写概括分析罗勒是一个什么样的人？ 例： 他注视着列车驶去，直到看不见时才转过身来，我发现他确实泪水盈眶。

不过他看到我，还是挺高兴。

他问我这些年来躲到哪儿去了，同时把半克朗钱还给我，好像它是昨天刚借去似的。

他挽住我的胳臂，顺月台慢慢走着，一面告诉我，每星期六他是何等欣喜地读我写的戏剧评论。

（真诚，诚信，友爱，善解人意。

） 对美国小姐：真诚慈爱，充满感情。

见到我之后：有教养，穿着得体， 极有风度。

还钱、翻本：诚实认真，聪明敬业。

* * * * * * * * * * * * * * * * * * * * * * * * 想一想我们学过的送别诗有那些？ 《送杜少府之任蜀州 》 王勃 《送孟浩然之广陵 》李白 《白雪歌送武判官归京》 岑参 城阙辅三秦，风烟望五津。

2009年厦门市高三质量检查测试九数学（理科）试题本试卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分．满分为150分，考试时间120分钟．注意事项：1． 考生将自己的姓名、准考证号及所有答案均填写在答题卡上； 2． 答题要求，见答题卡上的“填涂样例”和“注意事项”. 参考公式：如果事件A 、B 互斥，那么P （A+B ）=P （A ）+P （B ） 如果事件A 、B 相互独立，那么P （A·B ）=P （A ）·P （B ）如果事件A 在一次试验中发生的概率是P ，那么n 次独立重复试验中恰好发生k 次的概率P n (k)=C n k P k (1－P)n-k球的表面积公式：S=4πR 2，其中R 表示球的半径. 球的体积公式：V=34πR 3，其中R 表示球的半径. 第I 卷（选择题 共60分）一、选择题：本大题共12个小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的. 1．已知复数2121,1,21z z z i z i z ⋅=-=+=则在复平在上对应的点位于 （ ） A ．第一象限 B ．第二象限C ．第三象限D ．第四象限2．等差数列{a n }中，已知===+9375,4,16a a a a 则（ ） A ．8 B ．12 C ．24 D ．253．某市组织一次高三调研考试，考试后统计的数学成绩服从正态分布，其密度函数 )),((1021)(200)80(2+∞-∞∈⋅=-x ex f x π，则下列命题不正确的是（ ）A ．该市这次考试的数学平均成绩为80分B ．分数在120分以上的人数与分数在60分以下的人数相同C ．分数在110分以上的人数与分数在50分以下的人数相同D ．该市这次考试的数学标准差为104．设α、β、γ为互不相同的三个平面，l 、m 、n 为不重合的三条直线，则l ⊥β的一个充分不必要条件是 （ ） A ．l =⊥⊥γαγβγα ,, B ．m l m ⊥=⊥,,βαβα C ．αβα⊥⊥⊥l m m ,, D ．αγβγα⊥⊥⊥l ,, 5．已知在平面直角坐标系中，).3,2(),1,0(),21,1(),0,0(Q N M O 若动点),(y x P 满足不等式 OQ OP ON OP OM OP ⋅≤⋅≤≤⋅≤则,10,10的最大值为 （ ）A ．2B ．32C ．4D ．86．双曲线)0,0(12222>>=-b a by a x 的一条准线与两条渐近线交于A 、B 两点，相应的焦点为F ，若以AB 为直径的圆恰过F 点，则双曲线的离心率为 （ ）A ．2B ．332 C ．3D ．27．点)1,2(--P 到直线l ：λλλ52)21()31(+=+++y x 的距离为d ，则d 的取值范围是（ ）A ．130<≤dB ．0≥dC ．13>dD ．13≥d8．方程|3sin 2|22x x =-的实根的个数是 （ ）A ．4B ．6C ．8D ．129．已知函数)(x f y =的定义域为),3()3,(+∞--∞ ，且满足条件：369422=-y x ，其中)(.0x f y xy =<若的反函数)(x g y =的图象上任意一点的切线的斜率为k ，则k 的取值范围是（ ）A ．),3()3,(+∞--∞B ．)23,(--∞C ．),23(+∞-D ．)0,23(-10．若对任意长方体M ，都存在一个与M 等高的长方体N ，使得N 与M 的侧面积之比和体积之比都等于t ，则t 的取值范围是 （ ） A ．10≤<t B ．1≥t C ．21≤≤t D ．2≥t 11．若)(x f 是奇函数，且在（0，+∞）上是增函数，且0)2(=-f ，则0)(<⋅x f x 的解是 A ．（－2，0）∪（2，+∞） B ．（－∞，－2）∪（0，2） C ．（－∞，－2）∪（2，+∞） D ．（－2，0）∪（0，2）12．某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是( )(A)计算机行业好于化工行业. (B) 建筑行业好于物流行业.(C) 机械行业最紧张. (D) 营销行业比贸易行业紧张.第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4小题，每小题4分，共16分．在答题卡上的相应题目的答题区域内作答．13．已知向量x q p x q x p 若由且.),3,(),1,2(⊥-=-=的值构成的集合A 满足}2|{=⊇ax x A ,则a 的取值的集合是 .14．已知=-+=-+--++∞→→n n n n n x ba b a b x x ax x 11233lim ,33lim 则 . 15．正方体ABCD —A 1B 1C 1D 1的棱长为2，若球O 与正方体ABCD —A 1B 1C 1D 1有共同的中心，正方体在球内部的表面积为6π，则球O 的半径为 . 16．已知nn a )31(=，把数列{a n }的各项排成如右图所示三角形形状，记),(n m A 表示第m 行、第n 列的项，则=)8,10(A ，a 120在图中的位置为 .三、解答题：本大题共6小题，共74分，解答题应写出文字说明，证明过程或演算步骤，在答题卡上相应题目的答题区域内作答. 17．（12分）已知R m ∈，设命题P ：1x 和2x 是方程220x ax --=的两个实根，不等式||3521x x m -≥+对任意实数a ]1,1[-∈恒成立；:Q 函数++=23)(mx x x f+m (6)34+x 在区间(－∞,+∞)上有极值.求使P 正确且Q 也正确的m 的取值范围。

福建省2009年普通高中毕业班质量检查数学 (文科)试题本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)，共8页，全卷满分150分，考试时间120分钟． 参考公式：如果事件A 、B 互斥，那么P(A+B)=P(A)+P(B)． 如果事件A 、B 相互独立，那么P(A·B)=P(A)·P(B)．如果事件A 在一次试验中发生的概率是p ，那么n 次独立重复试验中恰好发生k 次的概率P n (k )=k n kk n )p (p C --1．球的表面积公式 S =4πR 2，其中R 表示球的半径． 球的体积公式 V =34πR 3，其中R 表示球的半径．第I 卷(选择题 共60分)一、选择题：本大题共12小题。

每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的。

请把正确答案填在题目后面的括号内．1．已知集合A={x |-2，-1，0,1，2}，B={2，3}，则A ∪B 为( )A ．{2}B ．{2，3}C ．{-2，-1，0,1，2}D ．{-2，-1，0,1，2，3} 2．不等式032>+-x x 的解集是( ) A ．(-3,2) B ．(2，+∞)C ．(-∞，-3)∪(2，+∞)D ． (-∞，-2)∪(3, +∞) 3．双曲线4x 2-y 2=1的渐近线方程是( )A ．4x ±y =0B ．x ±4y =0C ．x ±2y =0D ．2x ±y =0 4．已知函数),x (),x (x )x (f x0203>≤+=则f ( f (-2))的值为( )A ．-1B ．41C ．2D ．4 5．已知A 、B 为球面上的两点，O 为球心，且AB =3，∠AOB =120°，则球的体积为( ) A ．29π B ． π34 C ．36π D ． π3326．已知二次函数y=x 2-2ax+1在区间(2，3)内是单调函数，则实数a 的取值范围是( ) A ．a ≤2或a ≥3 B ．2≤a ≤3 C ． a ≤-3或a ≥-2 D ．-3≤a ≤-2 7．已知条件p : k =3，条件q ：直线y=kx +2与圆x 2+y 2=1相切，则p 是q 的( ) A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件8．已知数列{}n a 的前n 项和为S n ，且S n 是a n 与1的等差中项，则a n 等于( ) A ．1 B ．-1 C ．(-1)n D ．(-1)n-19．若m 、n 为两条不同的直线，α、β为两个不同的平面，则以下命题正确的是( ) A ．若m ∥α，m ⊂β，α∩β=n ，则m ∥n B ．若m ∥α，n ⊂α，则m ∥n C ．若m ∥α，n ∥α，则m ∥n D ．若α∩β =m ，m ⊥n ，则n ⊥α10．函数y=A sin(ωx+φ)图象的一部分如图所示，则此函数的解析式可以写成( ) A ．y =sin(x +8π)B ．y =sin(2x +8π)C ．y =sin(2x +4π)D ．y =sin(2x -4π)11．某小组有12名学生，其中男生8名，女生4名，从中随机抽取3名学生组成一兴趣小组，则这3 名学生恰好是按性别分层抽样得到的概率为 ( ) A ．3122418C C C B ．3121428C C C C ．3121428A A A D ．3121428A A A12．若函数f (x )为奇函数，且在(0，+∞)内是增函数，又f (2)=0，则x)x (f )x (f --＜0的解集为( )A ．(-2,0)∪(0,2)B ．(-∞，-2)∪(0,2)C ．(-∞，-2)∪(2，+∞)D ．(-2,0)∪(2，+∞)第Ⅱ卷(非选择题 共90分)二、填空题：本大题共4小题，每小题4分。

福建省厦门第一中学2009年高三春季质量检查数学（文科）试题选择题（12小题，每小题5分，共60分）1. 在等差数列仏｝中,勺+冬二匸则其前9项的和S9等于A. 18B. 27C. 36D. 92. 函数“）"nHcos — sinx ）的最小正周期为71 71A. 4B. 2C. 71D. “A = lx x-a Y 4] B兀一2）（3— 兀）ao| 3. 已知命题p: l'，命题q: I I 丿，且「p 是「q 的充分条件，则实数Q 的収值范围是： A. （-1,6）B.卜 1,6]C （-<x ）,-l ）u （6,+oo ）D . （一°°,一1]3[6,+8）4. 用系统抽样法从160名学牛中抽取容量为20的样木，将160名学牛从1-160编号，按编号顺序平均分成20组（[〜8号,9〜16号，…，153〜160号）。

若第16组应抽出的号码 为126,则第一组中用抽签方法确定的号码是 A. 4B. 5C. 6D. 732--- 715.已知一个球与一个正三棱柱的三个侧面和两个底面相切，若这个球的体积是3I = 0上，其中m 、n 均为正数，则加兀的最小值为7.已知直线1与圆C ：2 J 1 r+ r =1jl 沏于笫二象限,并H 直线1在两朋标轴上的截距之和,则这个三棱柱的体积是A. 96A/3B. 16馆C. 24迟D. 48馆6.在右图的程序框图屮，改程序框图输出的结果是28,则序号①应填入的条件是A. K>2 B・ K>3C. K>4D. K>5等于侖，贝悄线1与两坐标轴所围城的三角形的血'积为8.设°、0是两个平而，/、m 是两条直线，下列命题中，可以判断的是门1） + /（2）+ /（3）+…『（2008）的值为10.函数+ T （aA°"l ）的图像恒过定点A,若A 在直线mx + ny +1 2—I — 1若隊I 数/（人）=J1 -（x-2）2 + 2,对任意的西,勺，且2 Y 兀］Y 兀2 Y 3 ,那么有D. X lfM = X 2.f(X 2)天空题（每小题4分，共1 6分）在复平面内,复数1 + i 与一 1+3 i 分别对应向量OA^\OB 其中o 为坐标原点，贝ij咲] A. 6 71 B.［亍，兀］71 2龙 71 C. [TT ]D.訂 2A. 31 B. 2C- 1 或3丄或色 D. 2 2A I u u a,且Z||/?, m || 0 B.I (Z a.m cz 0,且加 || 0 C.側，阳|0且1|D.I 丄 ajn 丄 0，且/1| m 9.若定义在R 上的函数，（兀）图像关于点（一匸）成屮心对称，对任意的实数*都有且 /（T ）i/(0)= -2A. -2B. -1C.D. 1A. 2B. 4C. 6D. 8A 兀］/（兀2）»兀2/（兀1）B 兀】/（兀2）=勺/（兀】） 12.13.cosA= ________~—:_r = 116. 知F1F2是双曲线/ b2（a>0,b>0）的两个焦点，以线段Fl F2为边作正Z\MF1 F2,若边MF1的屮点在双III ］线上，则双|111线的离心率e 二 __________ 三.解答题（6大题，共74分）17. （12分）若函数/（兀）= sine 兀-sinorcos 亦（Q >0）的图像的任意两条对称轴之间的 （1）当XE ［0,4］时，求f （x ）的减区间；（2）若将函数f （x ）的图像向右71平移0 （0<°<2 ）个单位后所得函数为g （x ）,若g （x ）为偶函数，求©18. （12分）设函数/（兀）=处'+加+ °是定义在R 上的奇函数，且函数‘⑴的图像在 x=l 处的切线方程y=3x+2・（1）求断数/（兀）的表达式；（2）若对任意x*（°，l ］都有m14. 设等比例£ 1 V勺｝的前n 项和为几吒蔦‘牡15.在AABC 中，角 A 、 B 、C 所対的边分别为a 、b 、c,尹(yjib - c) cos A = a cos C,71距离的最小值为厅成立，求实数m的収值范围。