当前位置：文档之家 › 第二讲 双变量回归模型及其估计问题

第二讲 双变量回归模型及其估计问题

  • 格式：ppt
  • 大小：1.09 MB
  • 文档页数：45

下载文档原格式

  / 45

合集下载

第二章 双变量线性回归模型(计量经济学,南京审计学院)

第二章 双变量线性回归模型(计量经济学,南京审计学院)

2 2 t
n ,„ ,2
x

1 )0 x ( 2 2 ) tx
2 2 i 2 t
2 t
X
2 t
x
X 2 tx
2
三. 高斯--马尔柯夫定理
（Gauss--Markov Theorem）
对于满足统计假设条件(1)--(4)的线性回 归模型 Yt = + Xt + ut , ，普通最小二 乘估计量 ( OLS估计量) 是最佳线性无偏 估计量（BLUE, The Best Linear Unbiased Estimator）。
2 ˆ et (Yt Yt ) 2
最小二乘法
最小二乘法就是选择一条直线，使其残差平方和达 到最小值的方法。即选择 ˆ ，使得 ˆ和
2 ˆ S et (Yt Yt ) 2 2 ˆ ˆ (Yt X t )
达到最小值。
运用微积分知识，使上式达到最小值的必要条件 为：
第二章 双变量线性回归模型
（简单线性回归模型）
（Simple Linear Regression Model）
第一节 双变量线性回归模型的估计
一. 双变量线性回归模型的概念
设 Y = 消费, X = 收入, 我们根据数据画出散点图
Y * 这意味着 Y = + X (1) 我们写出计量经济模型 Y = + X + u (2) 其中 u = 扰动项或 误差项 Y为因变量或被解释变量 X为自变量或解释变量 和 为未知参数
双变量线性回归模型的统计假设
(1). E(ut) = 0, t= 1, 2, ...,n 即各期扰动项的均值(期望值)为0. (2). E(uiuj) = 0 i j 即各期扰动项互不相关. (3). E(ut2 ) = 2 , t= 1, 2, ...,n 即各期扰动项方差是一常数. (4). 解释变量Xt 为非随机量 即Xt的取值是确定的, 而不是随机的. (5). ut ~ N( 0, 2 ) , t= 1, 2, ...,n 即各期扰动项服从正态分布。
计量经济学双变量回归模型估计问题

计量经济学双变量回归模型估计问题

第三章
双变量回归分析：
估计问题
基本内容
普通最小二乘法（OLS） 经典线性回归模型：OLS的基本假定 OLS估计的性质 判定系数r2：“拟合优度”的一个度量
2
普通最小二乘法
（Ordinary Least Squares ，OLS）
最小二乘准则
ui2 (Yi Yi )2最小化
3
最小二乘准则
27
r2与r
r2
r
就模型而言
就两个变量而言
说明解释变量对因变量 的解释程度 度量不对称的因果关系
取值：[0,1]
度量两个变量线性依存 程度。
度量不含因果关系的对 称相关关系
取值：[－1,1]
28
运用r2时应注意
● 判定系数只是说明列入模型的所有解释变量对 因变量的联合的影响程度，不说明模型中每个 解释变量的影响程度（在多元中）
X
2 i
(
Xi )2
5
用离差表现的OLS估计式
为表达得更简洁，或者用离差形式OLS估计式：
__
__(Yi
__
Y
)
(Xi X )2
xi yi xi2
^
1
__
Y
ˆ2 X
注意其中： xi X i X
yi Yi Y
6
OLS估计量的良好性质
容易计算（由可观测的样本表达） 是点估计量 容易画出SRF，且SRF： （1）通过样本均值点
● 回归的主要目的如果是经济结构分析，不能只 追求高的判定系数，而是要得到总体回归系数 可信的估计量，判定系数高并不表示每个回归 系数都可信任。
29
Cov(Yi ,Yj ) 0(i j)
13
OLS估计的标准误（精度）
第2章 双变量回归模型(2)

第2章 双变量回归模型(2)

④单击确定，出现如下结果：
SUMMARY OUTPUT 回归统计 Multiple R0.940341 R Square 0.884241 Adjusted R0.878979 Square 标准误差 4.146637 观测值 24 方差分析 df 回归分析 残差 总计 SS MS 1 2889.552 2889.552 22 378.2811 17.1946 23 3267.833 F Significance F 168.05 8.9E-12
2 n i 1 i 1 2 i
2
问题转化为:在给定的样本观测值下，b1=?,b2=? 时，Q最小？
推导：
Q b 2 (Yi b1 b2 X i ) (1) 0 1 Q 2 (Y b b X ) ( X ) 0 i 1 2 i i b2
-973 1314090 1822500 947508 -929 975870 1102500 863784 -445 334050 562500 198381 -412 185580 202500 170074 -159 23910 22500 25408 28 4140 22500 762 402 180720 202500 161283 511 382950 562500 260712 1018 1068480 1102500 1035510 963 1299510 1822500 926599 5769300 7425000 4590020
3500 每 月 消 费 支 出 (元) 3000 2500 2000 1500 1000 500 0 0 500 1000 1500 2000 2500 3000 3500 4000 每月可支配收入(元) 每月家庭消费支出Y 条件均值Y* 样本1 预测 样本 样本2 预测 样本2
第二讲双变量回归模型及其估计问题

第二讲双变量回归模型及其估计问题

第二讲 双变量回归模型及其估计问题双变量回归分析基本概念四、 正态性假定：经典正态线性回归模型 五、 双变量回归的区间估计七、 回归分析的应用：预测问题 八、 双变量线性回归模型的延伸回归分析的基本性质三、 双变量回归分析估计问题六、 双变量回归的假设检验 4、第一节回归分析的性质•、回归释义回归分析是关于研究一个叫应变量的变量对另一个或几个中解释变量的变量的依赖关系，其目的在于通过后者的已知值或设定值去估计和预测前者的数值。

二、统计关系与确定关系统计关系处理的是随机变量，而确定关系处理的是确定性的变量。

三、回归与因果关系回归分析研究的是一个变量对另一个或几个称为解释变量的依赖关系，却不一定是因果关系。

四、回归与相关相关分析的主要目的在于研究变量之间统计线性关联的程度，将变量均视为随机变量。

回归分析的主要目的在于研究变量之间统计关联的形式，目的在于揭示被解释变量如何依赖解释变量的变化而变化的规律，将解释变量视为确定性的，而将被解释变量视为随机变量。

第二节双变量回归分析的基本概念(1)•、一个人为的例子例：假定一个总体由60户家庭组成。

为了研 究每周家庭消费支出Y 与每周税后可支配收入 X 的关系，将他们划分为10组。

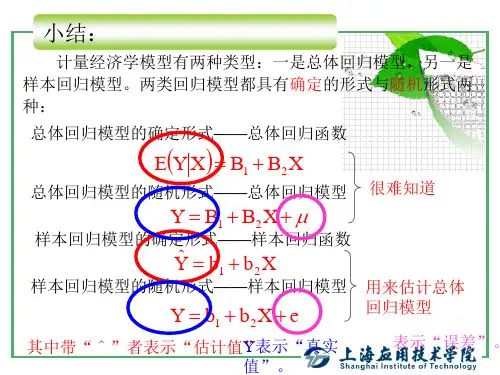
第二节二、总体回归函数(PRF)E(Y\X)=f(X)E(Y\X) = + 卩?X三、线性的含义对变量为线性E(Y\X) = fij + fi2X对参数为线性E(Y\X) = /3j + /32lnX1、总体回归函数的随机设定u = y-E(KIX)Y=E(Y\X)+ u系统变化部分非系统变化部分四、随机干扰项的意义干扰项“是从模型中省略下来的而又集体地影响着F的全部变量的替代物。

1.理论的含糊性 5.糟糕的替代变量2.数据的欠缺 6.节省原则3.核心变量与周边变量7.错误的函数形式4.人为行为的内在随机性五、样本回归函数(SRF)E(YIX)二Q + QX/V /v /VY =氏+卩字Y 仝 +£I =B\+B/+狂i i残差第三节双变量回归模型的估计问题•、普通最小二乘法通过样本数据按照残差平方和最小的原则来估计总体回归模型中的参数的方法叫普通最小二乘法，又称最小平方法。

chapter02线性回归模型双变量线性回归模型

chapter02线性回归模型双变量线性回归模型

每 960 月 家 庭 消 费 支 出 Y
E(Y Xi ) 900
1500 962 1024 1121 1210 1259 1324
1150
2000 1108 1201 1264 1310 1340 1400 1448 1489 1538 1600 1702
1400
每月家庭可支配收入X
2500 1329
◆是什么决定性的因素能使中国旅游业总收入到2020年达到 3000亿美元？
◆旅游业的发展与这种决定性因素的数量关系究竟是什么？
◆怎样具体测定旅游业发展与这种决定性因素的数量关系?
一、回归与相关
（对统计学的回顾）
1. 经济变量间的相互关系
◆确定性的函数关系 Y f (X )
◆不确定性的统计关系—相关关系
计量经济学关心：变量间的因果关系及隐藏在随 机性后面的统计规律性，这有赖于回归分析方法
4. 回归分析
回归的古典意义： 高尔顿遗传学的回归概念 ( 父母身高与子女身高的关系)
回归的现代意义： 一个应变量对若干解释变量 依存关系 的研究
回归的目的（实质）： 由固定的解释变量去 估计应变量的平均值
注意几个概念
2900 3150
例:100个家庭构成的总体 (单位:元)
1000 820 888 932
每 960 月 家 庭 消 费 支 出 Y
E(Y Xi ) 900
1500 962 1024 1121 1210 1259 1324
1150
2000 1108 1201 1264 1310 1340 1400 1448 1489 1538 1600 1702
1150
2000 1108 1201 1264 1310 1340 1400 1448 1489 1538 1600 1702
双变量回归

双变量回归

第三章
双变量回归模型：估计问题
简单的线性回归模型
Yi = 1 + 2 X i + ui
Yi = 每周家庭支出 X i = 每周家庭收入
对于给定的 xi的水平, 预期的食物支 出将是: E(Yi|X i) = 1 + 2 X i
参数
1和 2是未知常数.
^ ^ ) 的公 产生样本估计量 b1 (或 1)和 b2(或 2 式就是 1 和 2的估计。
b1 和b2的预期值
简单线性回归下的估计量的公式:
b2 =
nXiYi - XiYi nX2 -(Xi)2 i
xiyi = xi2
b1 = Y - b2X
这里
Y = Yi / n 和 X = Xi / n
将 Yi = 1 + 2xi + 替代到 b2 公式中并得:
ui
nxi ui - xi ui b2 = 2 + 2 2 nxi -(xi)

)2
=
yi
i
2
=
^

xi2 yi2
Sx2 Sy2
xiyi)2 xiyi 2 xi2 = = 2 2 xi2yi2 xi yi
Y
当R2 = 0 SRF
哪个是SRF ?Leabharlann X Y当 R2 = 1
SRF
SRF 通过所有点
X
高斯马尔可夫定理
在经典的线性回归模型条件下, 最小二乘 (OLS) 估计量 b1 和 b2 是1和 2 的最优线 性无偏估计量 (BLUE). 这意味着 b1和 b2 在1 和2所有线性无偏估计量中拥有 最小 方差.
错误的模型设定 先前的无偏结果假定使用了正确 的设定形式
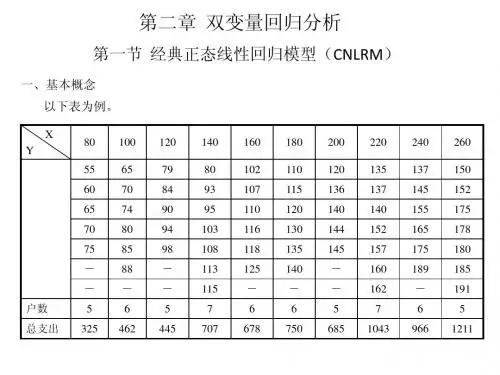
第二章 双变量回归分析(计量经济学,南开大学)

第二章 双变量回归分析(计量经济学,南开大学)


ˆ 和 ˆ 1 2

i
为Yi的线性函数
i 2 i
ˆ
2
xY x

(
xi )Yi 2 x i
k Y
i
i
其中k i
xi xi2 1 xi2
ki k i2
x

2
i
0
2 xi

1 xi2 1 xi2

i
1 xi2
6、样本回归函数（SRF） 由于在大多数情况下，我们只知道变量值得一个样本，要用样本信息的基础 上估计PRF。(表） 样本1
X（收入） Y（支出） 80 55 100 65 120 79 140 80 160 102 180 110 200 120 220 135 240 137 260 150
样本2
ˆ ) VAR( 2

x
2 i
2
2 i
x
ˆ： 对于 1
ˆ Y ˆ X 1 ˆ X Yi 1 2 2 n 1 ˆ X ( 1 2 X i ui ) 2 n u 1 i X k i ui n ˆ ) E[( ui X 方差：VAR( k i ui ) 2 ] 1 n
ˆ ) E( ki E (ui ) 2 2 2 ˆ Y ˆ X 1 2 ( 1 2 X i ui ) ( 1 k i u i ) X 1 u i X k i u i ˆ ) E( 1 1
1 1 2 21
估计量（Estimator）：一个估计量又称统计量(statistic)，是指一个规则、公式 或方法，以用来根据已知的样本所提供的信息去估计总体参数。在应用中，由估 计量算出的数值称为估计（值）（estimate)。 样本回归函数SRF的随机形式为：
第3章：双变量回归模型：估计问题

第3章：双变量回归模型：估计问题


（记Xi
X

xi,Yi Y

y
）
i
ˆ2

n n
X iYi
X
2 i

(
X i Yi X i)2

(X
i (X
X )(Yi i X )2
Y
)

xi yi
x
2 i
ˆ1
X
2 i
n
Y i
X
2 i

(
X i X iYi X i)2
Y
回归分析的目的：是运用样本数据估计SRL， 使SRL能最大限度逼近于PRL。
由此而提出的问题是，在什么假定下，运用何 种方法形成SRL，使SRL尽可能逼近PRL。
暨南大学经济学院统计系 陈文静
3
由
于
u
是
i
样
本
点
对
总
体
回
归
直
线
的
偏
差
，
自
然
地
希
望
基
于
u
i
来
实
现
这
一
目
的
。
由
于
u
的
i
估
计
uˆi
度
( uˆi2) / ˆ2 ( (Yi ˆ1 ˆ2Xi )2) / ˆ2 2 (Yi ˆ1 ˆ2Xi )Xi 2 uˆi Xi 0
暨南大学经济学院统计系 陈文静
9
进一步可以得出：
2 (Y i ˆ1 ˆ 2 X i ) 2 uˆ i 0
X i)2 n
第3章：双变量回归模型：估计问题

第3章：双变量回归模型：估计问题


最小二乘估计
1. 德国科学家Karl Gauss(1777—1855)提出用 德国科学家Karl Gauss(1777—1855)提出用 最小化图中垂直方向的误差平方和来估计参数
2. 使因变量的观察值与估计值之间的离差平方 ˆ ˆ 和达到最小来求得β 0 和 β1的方法。即
ˆ ˆ ˆ ˆ ˆ ˆ min ∑ (ui ) 2 = ∑ (Yi − Yi ) 2 = ∑ (Yi − β1 − β 2 X i ) 2 = f ( β1 , β 2 )
回归分析的目的：是运用样本数据估计SRL， 回归分析的目的：是运用样本数据估计SRL，使 SRL SRL能最大限度逼近于PRL。 能最大限度逼近于PRL SRL能最大限度逼近于PRL。 由此而提出的问题是，在什么假定下，运用何种 由此而提出的问题是，在什么假定下， 方法形成SRL SRL， SRL尽可能逼近PRL？ 尽可能逼近PRL 方法形成SRL，使SRL尽可能逼近PRL 注意：总体回归函数或直线是：固定的、唯一的 且是未知的。而我们每抽取一个样本，就可以得 出一条样本回归直线，所以样本回归直线不是固 定的，会随着样本的不同而不同，且是已知的， 估计思路就是用已知的或者可以获得的信息来估 计未知的总体信息。
i i i 2 i 2
∑ X ∑Y ∑XY −
i i i
i
1 （均值X = ∑ X i） n
2
∑ X Y − X ∑ Y （ (∑ X ) = n ∑ X − nX ∑Y ( X − X ) = ∑ X − nX ∑ ( X − X )(Y − Y ) = ∑(X − X )
i i i 2 i i 2 i 2 i
i i i 2 i 2 i
i
X i2 ∑ Y i − ∑ X i ∑ X iYi ∑ n∑ X i2 − (∑ X i ) 2
第2章_线性回归的基本思想：双变量模型 (2)

第2章_线性回归的基本思想：双变量模型 (2)


200 35 31 30 28 26 22 20
225 36 34 31 29 27 26 23
250 38 36 33 30 28 25 23
275 40 37 32 30 29 27 25
300 42 39 34 31 30 29 26
325 43 35 31 30 29 33 32
350 375 45 39 33 30 27 30 28 46 40 34 31 28 32 30
2019/2/21
R 2 0.99
2
回归分析可以用来：
1、找到被解释变量(Y)与解释变 量(X)运动的相互关系，并检验 某些假设 如：固定其它条件不变，施肥 量每增加一单位, 收成变化多 少？是增收还是减产？ 2、在已知解释变量(X)的基础上， 估计或预测被解释变量(Y)的均 值 如：估计身高170的父亲，其 儿子的平均身高 3、综合分析、指导决策
随机干扰项的性质和意义 Yi B1 B2 X i ui
它是从模型中省略下来，但又集体地影
响着Y的全部变量的替代物。
博 彩 支 出
系统成分/定性：可支配收入（X） 其它变量的影响 如性格、年龄、 性别
B1＋B2 X i
非系统/随机成分:
ui
另外一些说不清的随机事件： 如某几天心情好，多买点
slope
Regression coefficients
12
2019/2/21
度量了X每变动一单位，Y（条件） 均值的变化率
2、总体回归函数（PRF）
（Population Regression Function）
条件回归分析
E（Y Xi ）＝B1＋B2 X i
E（ Y ）
B1
第3章 双变量回归模型：估计问题.ppt

第3章 双变量回归模型：估计问题.ppt


() 式乘以 Xi ，() 式乘以n，得
请大家自己推导一次
贵州财经大学经济研究所 白万平 教授


Xi
Yi ˆ1n
X i ˆ2
2
Xi
(1)

n X i Yi ˆ1n X i ˆ2n X i 2 (2)
（2）－（1）得 :
n X iYi X i Yi ˆ2[n X i 2 X i 2 ]
贵州财经大学经济研究所 白万平 教授
假定5：各个干扰之间无自相关
给定任意两个X值，Xi和Xj，ui和uj之间的相关为零
注：
xi yi (Xi X )(Yi Y ) XiYi X Yi Y Xi nXY
其中 Xi nX Yi nY
上式 XiYi 2nXY nXY

n X iYi nXY
X iYi X i n
Yi
xi2 (Xi X )2 Xi2 2X Xi nX 2
Xi nX
上式
Xi2 2nX 2 nX 2
n Xi 2 nX 2
Xi2 n
2
Xi
贵州财经大学经济研究所 白万平 教授
返回
OLS估计量的数值性质：
Ⅰ．OLS估计量是纯粹可以用可观测的样本量（指X和Y）表达的， 因此，这些量是比较容易计算的
可以表达为离差形式（deviation form）:
yi ˆ2 xi uˆi
证明： 我们已知有：
Y ˆ1 ˆ2 X
（2.6.2）式减去（3.1.12）式得：
(Yi Y ) ˆ2 (Xi X ) uˆi

【精品】第二章：双变量线性回归分析

第三部分初计量经济(13周）经典单方程计量经济模型:一元线形回归模型经典单方程计量经济模型：多元线形回归模型经典单方程计量经济模型:放宽基本假定模型第一章一元线性回归（双变量）(1）回归分析的基本概念（2)前提建设（3）参数估计：OLS的参数估计ML的参数估计（4）统计检验（5）预测(6）时间案例与操作(7）思考与作业§1经典正态线性回归模型(CNLRM）1、一个例子注x 表示收入，y 表示支出。

5010015020050100150200250300XYY vs. X5010015020050100150200250300XY 1Y1 vs. X条件分布：以X 取定值为条件的Y 的条件分布 条件概率：给定X 的Y 的概率，记为P （Y ｜X)。

例如，P （Y=55|X=80)=1/5；P （Y=150|X=260）=1/7。

条件期望（conditionalExpectation ）:给定X 的Y 的期望值，记为E(Y|X ）。

例如,E （Y ｜X=80）=55×1/5＋60×1/5＋65×1/5＋70×1/5＋75×1/5＝65总体回归曲线(Popular RegressionCurve ）（总体回归曲线的几何意义）：当解释变量给定值时因变量的条件期望值的轨迹。

总结总体：总体函数:总体方程：样本：样本函数：样本方程：2、3、总体回归函数（PRF）E（Y｜X i)=f(X i）当PRF的函数形式为线性函数,则有，E(Y|X i）=β1+β2X i其中β1和β2为未知而固定的参数，称为回归系数。

β1和β2也分别称为截距和斜率系数。

上述方程也称为线性总体回归函数.4、P RF的随机设定将个别的Y I围绕其期望值的离差（Deviation)表述如下:u i=Y i-E(Y|X i）或Y i=E(Y|X i）+u i5、其中u i是一个不可观测的可正可负的随机变量，称为随机扰动项或随机误差项.6、“线性”的含义“线性”可作两种解释：对变量为线性，对参数为线性。

双变量回归模型估计问题 (2)


xy x y
i i 2 i
2 2 i
r2的快捷 计算公式
ESS r 2 TSS=r 2 yi2 RSS=(1 r 2 ) yi2
T S S =E S S +R S S
y
2 i
=r y (1 r ) y
2 2 i 2
2 i
一个与判定系数r2 紧密相关但是概念上却 不同的统计量是样本相关系数r
Y
Yi Y
ˆi u
ˆ ˆX ˆ SRF : Y i 1 2 i
ˆ Y Y i
X
Xi
X
TSS=ESS+RSS
ESS RSS 1= + TSS TSS
i
ˆ Y Y ˆ u + Y Y Y Y
2 2 i 2 i i
2
定义： r Y Y
ˆ Y i
ˆj u
Xi
Xj
Xk
X
ˆ 合理吗？ ˆi Yi Y min u i
ˆ ˆ u Y Y i i
2 i i


min
ˆ ˆ X Y
2 1 2 i
2
最小 平方 least squares
最小二乘法
最小化
ˆ , ˆ ˆ u f 1 2



2

2
ˆ yy ˆ y y
i i 2 i
2 2
i
X X Y Y X X xy x
i i i 2 i
ˆ
1
X Y X X Y n X X

计量经济学ch2 双变量模型：系数估计


拍卖方式有英格兰式拍卖、荷兰式拍卖、 英格兰式与荷兰式相结合的拍卖方式。
英格兰拍卖也称“增价拍卖”或“低估价 拍卖”。是指在拍卖过程中，拍卖人宣布 拍卖标的的起叫价及最低增幅，竞买人以 起叫价为起点，由低至高竞相应价，最后 以最高竞价者以三次报价无人应价后，响 槌成交。但成交价不得低于保留价。
效率工资理论。效率工资理论认为工人 工作的效率与工人的工资有很大的相关性。 效率工资理论认为，高工资使工人效率更 高。目前，主要存在四种效率工资理论的 解释：
第一种解释适用于穷国的效率工资理论认 为，工资影响营养。多给工人点工资，工 人才吃得起营养更丰富的食物，而健康的 工人生产效率更高；
第二种适用于发达国家的效率工资认为， 高工资减少了劳动的流动性。工人由于许 多原因离职--接受其他企业更好的职位，改 变职业，或者迁移到其他地方。企业向工 人支付的工资越高，留在企业的激励越大。 企业通过支付高工资减少了离职的频率， 从而减少了雇佣和培训新工人的时间和费 用。
OLS估计原理
对方程
min ei2
Yi b1 b2 Xi 2
求导，并令其为零，得到方程组：
Yi nb1 b2 X i
Yi X i b1
X i b2
X
2 i
其中 n 为样本容量。
四、参数估计原理
求解，得到斜率的估计量
b2
xi yi xi2
X i X Yi Y
2
Xi X
xi X i X ; yi Yi Y 为离差。
经济计量过程
理论和假说 变量选择 数据6-14 散点图 估计和结果 结论的经济意义
五、案例5：工资和生产率关系
理论分析 数据表7-3 散点图 估计和结果 结论的经济意义

第二章双变量线性回归分析

[计量经济学] 第二章：双变量线性回归分析§1 经典正态线性回归模型（CNLRM）一、一些基本概念1、一个例子条件分布：以X取定值为条件的Y的条件分布条件概率：给定X的Y的概率，记为P(Y|X)。

例如，P(Y=55|X=80)=1/5；P（Y=150|X=260）=1/7。

条件期望（conditional Expectation）：给定X的Y的期望值，记为E(Y|X)。

例如，E(Y|X=80)=55×1/5＋60×1/5＋65×1/5＋70×1/5＋75×1/5＝65总体回归曲线（Popular Regression Curve）（总体回归曲线的几何意义）：当解释变量给定值时因变量的条件期望值的轨迹。

2、总体回归函数（PRF）E(Y|X i)=f(X i)当PRF的函数形式为线性函数，则有，E(Y|X i)=β1+β2X i其中β1和β2为未知而固定的参数，称为回归系数。

β1和β2也分别称为截距和斜率系数。

上述方程也称为线性总体回归函数。

3、PRF的随机设定将个别的Y I围绕其期望值的离差(Deviation)表述如下：u i=Y i-E(Y|X i)或Y i=E(Y|X i)+u i其中u i是一个不可观测的可正可负的随机变量，称为随机扰动项或随机误差项。

4、“线性”的含义“线性”可作两种解释：对变量为线性，对参数为线性。

本课“线性”回归一词总是指对参数β为线性的一种回归（即参数只以它的1次方出现）。

模型对参数为线性？模型对变量为线性？是不是是LRM LRM不是NLRM NLRM注：LRM＝线性回归模型；NLRM＝非线性回归模型。

5、随机干扰项的意义随机扰动项是从模型中省略下来的而又集体地影响着Y 的全部变量的替代物。

显然的问题是：为什么不把这些变量明显地引进到模型中来？换句话说，为什么不构造一个含有尽可能多个变量的复回归模型呢？理由是多方面的： （1）理论的含糊性 （2）数据的欠缺（3）核心变量与周边变量 （4）内在随机性 （5）替代变量 （6）省略原则（7）错误的函数形式6、样本回归函数（SRF ） （1）样本回归函数iY ˆ=1ˆβ+2ˆβi X 其中Y ˆ＝E(Y|X i )的估计量；1ˆβ＝1β的估计量；2ˆβ＝2β的估计量。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
东北财经大学数学与数量经济学院
第三节
双变量回归模型的估计问题（3）
ˆ2 u ˆ b ˆ X) 0 2 (Y b 1 2 ˆ b1 ˆ +b ˆ X Y nb 1 2 ˆ2 u ˆ b ˆ X )( X ) 0 2 (Y b 1 2 ˆ b 2
240 260 137 150 145 152 155 175 165 178 175 180 189 185 191
Y
70 75
东北财经大学数学与数量经济学院
250
200
150
100
50
0 0 50 100 150 200 250 300
东北财经大学数学与数量经济学院
第二节
双变量回归分析的基本概念（2）
ˆ X +b ˆ X2 XY b 1 2
东北财经大学数学与数量经济学院
第三节
双变量回归模型的估计问题（4）
n XY X Y ˆ b2 2 2 n X ( X )
( X X )(Y Y ) xy 2 2 ( X X ) x
X Y X XY ˆ b1 2 2 n X ( X )
一、普通最小二乘法
东北财经大学数学与数量经济学院
第三节
双变量回归模型的估计问题（2）
2 2 ˆ ˆ u (Y Y )
ˆ b ˆ X )2 (Y b 1 2
ˆ2 u ˆ b ˆ X) 0 2 (Y b 1 2 ˆ b1
min
ˆ2 u ˆ b ˆ X )( X ) 0 2 (Y b 1 2 ˆ b 2
二、总体回归函数(PRF)
E (Y | X ) = f ( X )
E ( Y | X ) = b1 + b2 X
三、线性的含义
对变量为线性 E (Y | X ) = b1 + b2 X 对参数为线性 E (Y | X ) = b1 + b2 lnX
东北财经大学数学与数量经济学院
第二节
双变量回归分析的基本概念（3）
120 79 84 90 94 98
140 80 93 95 103 108 113 115
160 102 107 110 116 118 125
180 110 115 120 130 135 140
200 120 136 140 144 145
220 135 137 140 152 157 160 162
东北财经大学数学与数量经济学院
第一节
回归分析的性质（3）
四、回归与相关
相关分析的主要目的在于研究变量之间统 计线性关联的程度，将变量均视为随机变量。 回归分析的主要目的在于研究变量之间统 计关联的形式，目的在于揭示被解释变量如何 依赖解释变量的变化而变化的规律，将解释变 量视为确定性的，而将被解释变量视为随机变 量。
东北财经大学数学与数量经济学院
第三节
双变量回归模型的估计问题（6）
样本回归线的性质
1.它通过Y和X的样本均值； 2.估计的均值等于实测均值，即 3.பைடு நூலகம்差的均值等于0，即
ˆ Y Y
ˆ 0 u
ˆy ˆ 4.残差和预测值不相关，即 u
三、总体回归函数的随机设定
u = Y - E (Y | X ) Y = E (Y | X ) + u
系统变 化部分 非系统变化部分
东北财经大学数学与数量经济学院
第二节
双变量回归分析的基本概念（4）
四、随机干扰项的意义
干扰项 u 是从模型中省略下来的而又集 体地影响着Y 的全部变量的替代物。
1.理论的含糊性
残差
东北财经大学数学与数量经济学院
第三节
双变量回归模型的估计问题（1）
第三节
60 50 40 30 20 10 0 0 2 4 6
双变量回归模型的估计问题
通过样本数据 按照残差平方和最 小的原则来估计总 体回归模型中的参 数的方法叫普通最 小二乘法，又称最 小平方法。
8 10 12 14 16 18
第二讲
双变量回归模型及其估计问题
一、回归分析的基本性质 二、双变量回归分析基本概念 三、双变量回归分析估计问题
四、正态性假定：经典正态线性回归模型 五、双变量回归的区间估计 六、双变量回归的假设检验 七、回归分析的应用：预测问题 八、双变量线性回归模型的延伸
东北财经大学数学与数量经济学院
第一节
回归分析的性质（1）
2.数据的欠缺 3.核心变量与周边变量
5.糟糕的替代变量 6.节省原则 7.错误的函数形式
4.人为行为的内在随机性
东北财经大学数学与数量经济学院
第二节
双变量回归分析的基本概念（5）
五、样本回归函数(SRF)
E ( Y | X ) = b1 + b2 X
ˆ +b ˆ X ˆb Y 1 2 ˆ +b ˆ X +u ˆ +u ˆb ˆ Y Y 1 2
第一节
一、回归释义
回归分析的性质
回归分析是关于研究一个叫应变量的变 量对另一个或几个中解释变量的变量的依赖 关系，其目的在于通过后者的已知值或设定 值去估计和预测前者的数值。
东北财经大学数学与数量经济学院
第一节
回归分析的性质（2）
二、统计关系与确定关系 统计关系处理的是随机变量，而确 定关系处理的是确定性的变量。 三、回归与因果关系 回归分析研究的是一个变量对另一 个或几个称为解释变量的依赖关系，却 不一定是因果关系。
2
ˆ Y b ˆ X b 1 2
东北财经大学数学与数量经济学院
第三节
数值性质
双变量回归模型的估计问题（5）
是指由于运用最小二乘法而得以成立的那 些性质而不管数据是如何产生的。
统计性质
是指仅在数据产生的方式满足一定的假设 下才得以成立的那些性质。
数 值 性 质
1.OLS估计量是纯粹由可观测的量表达式，是容易计算的； 2.OLS估计量是点估计量； 3.一旦从样本数据得到OLS估计值，便可画出样本回归线。
东北财经大学数学与数量经济学院
第二节
双变量回归分析的基本概念（1）
第二节
双变量回归分析的基本概念
一、一个人为的例子
例： 假定一个总体由60户家庭组成。为了研 究每周家庭消费支出Y与每周税后可支配收入 X的关系，将他们划分为10组。
东北财经大学数学与数量经济学院
x
80 100 55 60 65 65 70 74 80 85 88