当前位置：文档之家 › 双变量回归模型基本概念

双变量回归模型基本概念

  • 格式：pptx
  • 大小：703.27 KB
  • 文档页数：39

下载文档原格式

  / 39

合集下载

第二章 双变量模型

第二章 双变量模型

概念： 概念：
在给定解释变量Xi条件下被解释变量Yi的期 望轨迹称为总体回归线 总体回归线（population 总体回归线 regression line），或更一般地称为总体回 总体回 归曲线（population regression curve）。 归曲线 相应的函数： E (Y | X i ) = f ( X i ) 称为（双变量）总体回归函数（population 总体回归函数（ 总体回归函数 regression function, PRF）。 ）
变量间的关系
经济变量之间的关系，大体可分为两类： （1）确定性关系 函数关系：研究的是确定 确定性关系或函数关系 确定性关系 函数关系： 现象非随机变量间的关系。
相关关系： （2）统计依赖 相关关系： 研究的是非确定现 ）统计依赖或相关关系 象随机变量间的关系。
回归与相关
相关分析的主要目的在于研究变量之间统计 线性关联的程度，将变量均视为随机变量。 回归分析的主要目的在于研究变量之间统计 关联的形式，目的在于揭示被解释变量如何依赖 解释变量的变化而变化的规律，将解释变量视为 确定性的，而将被解释变量视为随机变量。
二、回归分析的基本概念
回归分析(regression analysis)是研究一个变量关 回归分析 是研究一个变量关 于另一个（ 于另一个（些）变量的具体依赖关系的计算方法 和理论。 和理论 其用意：在于通过后者的已知或设定值， 其用意：在于通过后者的已知或设定值，去估计和 预测前者的（总体）均值。 （或）预测前者的（总体）均值 这里：前一个变量被称为被解释变量（Explained 被解释变量（ 被解释变量 Variable）或应变量（Dependent Variable）， 应变量（ ） 应变量 ）， 后一个（些）变量被称为解释变量 解释变量 （Explanatory Variable）或自变量 ） 自变量 （Independent Variable）。 ）

第2章：线性回归的基本思想：双变量模型

第2章：线性回归的基本思想：双变量模型
如： P(Y=460|X=5000）=1/5。
因此，给定收入X的值Xi，可得分数Y的条件均值 （ conditional mean ） 或 条 件 期 望 （ conditional
expectation）：
2-17
E(Y|X=Xi)
2.2 总体归函数（PRF）：假想一例
描出散点图发现：随着收入的增加，成绩“平均 地说”也在增加，且Y的条件均值均落在一根正斜 率的直线上。这条直线称为总体回归线。
皮尔逊收集过一些家庭群体的1千多名成员的身 高记录。他发现，对于一个父亲高的群体，儿 辈的平均身高低于他们父辈的身高，而对于一 个父亲矮的群体，儿辈的平均身高则高于其父 辈的身高。这样就把高的和矮的儿辈一同“回 归”到所有男子的平均身高。用加尔顿的话说， 这是“回归到中等”。
2-2
2.1 回归的含义
对变量间统计依赖关系的考察主要是通过相关分析 (correlation analysis) 和 回 归 分 析 (regression analysis)来完成的：
正相关
线性相关 不相关 相关系数：
统计依赖关系
2-4
负相关 1 XY 1
正相关 非线性相关 不相关
负相关
有因果关系 无因果关系
回归分析 相关分析
经济变量之间的关系，大体可分为两类： （1）确定性关系或函数关系：研究的是
确定现象非随机变量间的关系。
（2）统计依赖或相关关系：研究的是非确 定现象随机变量间的关系。
2-3
2.1 回归的含义
例如：
函数关系： 圆面积 f ,半径 半径2
统计依赖关系/统计相关关系：
农作物产量 f 气温, 降雨量, 阳光, 施肥量
2-23
2.3 总体回归函数的统计或随机设定

第三章 双变量线性回归模型

第三章 双变量线性回归模型
（2）两变量之间的关系可能不是严格线性的，u反 映了与直线的偏差。
（3）经济行为是随机的，我们能够用 Y=α+βX 解释“典型”的行为，而用u来表示个体偏差。 （4）总会出现测量误差， 使得任何精确的关系不 可能存在。
二. 普通最小二乘法(OLS法, Ordinary Least squares)
（2）E(uiuj) = 0, i≠j 即各期扰动项互不相关。也就是假定它们之间无
自相关或无序列相关。
实际上该假设等同于：
cov( uI, uj) = 0, i≠j 这是因为：cov(uI, uj) = E{[ui - E(ui)][uj - E(uj)]}
= E(uiuj) ——根据假设（1）
（3）E(ut2)= 2, t=1,2,…,n 即各期扰动项的方差是一常数，也就是假定各
（5）ut ~ N( 0, 2 ) , t= 1, 2, ...,n 即扰动项服从正态分布。
满足条件（1）—（4）的线性回归模型称为古典线 性回归模型（CLR模型）。
2.最小二乘原理
我们的任务是， 在给定X和Y的一组观测值 (X1, Y1), (X2, Y2) , ..., (Xn, Yn) 的情况下,
Yt = + Xt + ut
序号 1
2
3
4
5
Yt 14 18 23 25 30
Xt 10 20 30 40 50
解：我们采用列表法计算。计算过程如下：
Yt
1
14
2
18
3
23
4
25
5
30
Σ
110
Xt
yt Yt Y xt Xt X
xt yt
xt 2
10

第二章 双变量回归分析(计量经济学,南开大学)

第二章 双变量回归分析(计量经济学,南开大学)

ˆ 和 ˆ 1 2

i
为Yi的线性函数
i 2 i
ˆ
2
xY x

(
xi )Yi 2 x i
k Y
i
i
其中k i
xi xi2 1 xi2
ki k i2
x

2
i
0
2 xi

1 xi2 1 xi2

i
1 xi2
6、样本回归函数（SRF） 由于在大多数情况下，我们只知道变量值得一个样本，要用样本信息的基础 上估计PRF。(表） 样本1
X（收入） Y（支出） 80 55 100 65 120 79 140 80 160 102 180 110 200 120 220 135 240 137 260 150
样本2
ˆ ) VAR( 2

x
2 i
2
2 i
x
ˆ： 对于 1
ˆ Y ˆ X 1 ˆ X Yi 1 2 2 n 1 ˆ X ( 1 2 X i ui ) 2 n u 1 i X k i ui n ˆ ) E[( ui X 方差：VAR( k i ui ) 2 ] 1 n
ˆ ) E( ki E (ui ) 2 2 2 ˆ Y ˆ X 1 2 ( 1 2 X i ui ) ( 1 k i u i ) X 1 u i X k i u i ˆ ) E( 1 1
1 1 2 21
估计量（Estimator）：一个估计量又称统计量(statistic)，是指一个规则、公式 或方法，以用来根据已知的样本所提供的信息去估计总体参数。在应用中，由估 计量算出的数值称为估计（值）（estimate)。 样本回归函数SRF的随机形式为：

双变量回归模型(一元线性回归模型)

双变量回归模型(一元线性回归模型)

* * * * * * * * * *
* * * * * * * * * *
* * ** * * *
* * * * * * * * * *
总体回归曲线
E (Y X i ) f ( X i )
E (Y X i ) 1 2 X i
150 175 200 225 250 275 300 325 350 375 每周个人可支配收入（ X）
每周个人可支配收入（ X）
总体回归模型的随机形式
Yi 1 2 X i ui
随机总体回归函数
Yi可表示成两部分之和 系统成分（确定性成分）：1 2 X i 非系统成分（随机成分）：ui
引入随机干扰项的意义
1、理论的不完全性
与因变量相关的因素很多，随机干扰项替代了 未纳入模型的全部变量。

X
Xi
总体回归函数
E (Y X i ) 1 2 X i
1、 2为“未知但固定”的参数, 称为“回归系数” 。 1称为截距( Intercept ), 2 称为斜率( Slope)
斜率度量了解释变量X每变动一个单位， 因变量Y的条件均值变化多少个单位。 截距项度量了解释变量为零时因变量 的条件均值。一般来说，不解释其经 济意义。 该形式的总体回归函数称为
双变量回归模型
（一元线性回归模型）
双变量回归模型
（最简单的回归模型）
模型特点 因变量（Y）仅依赖于唯一的一个解释变量(X)。 回归分析的内容与目的 1、通过样本数据去估计出因变量与解释变量的统 计依赖关系式（总体回归函数）； 2、给定解释变量的取值，去估计因变量的均值； 3、假设检验； 4、根据样本外解释变量的取值，预测因变量的均 值。

bivariate logistic models双变量逻辑模型 -回复

bivariate logistic models双变量逻辑模型 -回复

bivariate logistic models双变量逻辑模型-回复什么是双变量逻辑模型?双变量逻辑模型是一种用于探索两个变量间关系的统计分析方法。

它的主要目的是通过研究两个二元变量的关系来推断一个变量对另一个变量的影响程度。

在实际应用中，双变量逻辑模型常常被用于解决因果关系和关联关系的问题。

本文将一步一步回答关于双变量逻辑模型的各种问题。

第一步：理解双变量逻辑模型的基本概念双变量逻辑模型是通过一种称为逻辑回归的方法来建模的。

逻辑回归是统计学中常用的一种回归分析技术，用于预测某个二元变量的概率。

通常情况下，双变量逻辑模型包括两个主要的变量：自变量和因变量。

自变量是用于预测因变量的变量，而因变量则是我们希望了解的结果或者感兴趣的现象。

第二步：确定研究问题和收集数据在使用双变量逻辑模型之前，我们需要确定一个明确的研究问题，并收集相应的数据来回答这个问题。

数据的收集可以通过实地调查、问卷调查或者其他适当的方法进行。

例如，我们想要研究自己的学术成绩是否受到每天的睡眠时间的影响。

在这种情况下，我们可以将学术成绩作为因变量，睡眠时间作为自变量，收集一定数量的样本数据来进行研究。

第三步：进行统计分析在得到数据之后，我们可以使用逻辑回归方法来进行统计分析。

逻辑回归主要用于估算自变量对因变量的影响程度，并得出相关的统计结论。

逻辑回归模型的核心是逻辑函数，也称为sigmoid函数。

这个函数的输出范围在0到1之间，表示某一事件发生的概率。

逻辑回归通过最大似然估计的方法来确定模型的参数，从而得出自变量对因变量的影响。

第四步：解读统计结果在进行统计分析之后，我们需要解读得到的结果。

逻辑回归模型通常会给出自变量与因变量之间的系数，这些系数可以用来衡量自变量对因变量的影响程度。

系数的正负决定了自变量对因变量概率的相对影响。

如果系数为正，表示自变量的增加会增加因变量发生的概率；如果系数为负，表示自变量的增加会减少因变量发生的概率。

3.1双变量线性回归分析的基本概念



随机误差项的意义（引入原因） （1）理论的含糊性； （2）数据的欠缺； （3）众多细小因素对因变量的综合影响； （4）变量的观测误差的影响； （5）模型设定误差的影响； （6）变量内在随机性的影响； （7） 省略原则。
回归模型存在两个特点：
建立在某些假定条件不变前提下抽象出来 的回归函数不能百分之百地再现所研究的 经济过程。 也正是由于这些假定与抽象，才使我们能 够透过复杂的经济现象，深刻认识到该经 济过程的本质。
由上图发现：随着收入的增加，消费支出Y“平 均地说”也在增加，且Y的条件均值均落在一根 正斜率的直线上。这条直线称为总体回归直线。
概念（二）
当解释变量Xi取给定值时因变量Yi的条件期望 值或条件均值的轨迹称为总体回归曲线 （population regression curve）。 总体回归直线（Population regression line, PRL ）
二、线性的含义
线性回归模型有两种解释： （1）对变量为线性 （2）对参数为线性

三、 PRF的随机设定以及随机误差项的性质 和意义
PRF说明了在给定的收入水平下，该社区家庭的 平均消费支出随收入变化的规律。 但对某一个别的家庭，其消费支出可能与该平均 水平有偏差。 ui Yi E(Y | X i )
总体回归函数PRF的随机设定形式 含义：它表明因变量除了受解释变量的系统 性影响外，还受其他因素的随机性影响。 由于函数中引入了随机项，成为计量经济学 模型，因此也称为总体回归模型。
随机误差项的性质

随机误差项是所有可能影响因变量，但又 未能包括到回归模型中来的被忽略变量的 替代(surrogate)或代理(proxy)变量。 E(ui| Xi)＝0

线性回归分析——双变量模型

线性回归分析——双变量模型在进行线性回归分析之前，我们首先需要明确我们要解决的问题，确定自变量和因变量。

比如，我们可以研究体重和身高之间的关系，其中体重是因变量，身高是自变量。

收集到数据后，我们可以进行描述性统计分析来对数据进行初步的了解。

我们可以计算出体重和身高的平均值、方差、最大值和最小值等统计指标。

此外，我们还可以绘制散点图来观察变量之间的关系。

在进行线性回归分析之前，我们需要满足一些假设条件。

首先，我们假设自变量和因变量之间存在线性关系。

其次，我们假设观测误差服从正态分布。

最后，我们假设观测误差的方差是常数。

接下来，我们可以通过最小二乘法来估计线性回归模型的参数。

最小二乘法的目标是最小化观测值与预测值之间的残差的平方和。

我们可以使用统计软件或者编程语言来进行计算。

线性回归模型可以表示为：Y=β0+β1X+ε其中，Y表示因变量，X表示自变量，β0表示截距，β1表示斜率，ε表示观测误差。

在进行参数估计后，我们可以对模型进行拟合优度的评估。

拟合优度指标可以帮助我们判断模型的拟合程度。

常见的拟合优度指标有R方值、调整R方值和残差分析。

R方值表示因变量的变异程度可以由自变量解释的比例。

R方值的取值范围是0到1，越接近1表示模型的拟合效果越好。

调整R方值是在R方值的基础上考虑模型中自变量的个数进行修正。

残差分析可以用来评估模型中未解释的部分。

在进行结果解释时，我们需要注意解释截距和斜率的意义。

截距表示当自变量为0时，因变量的值。

斜率表示自变量的单位变化对因变量的影响。

最后，我们还可以对模型的统计显著性进行检验。

常见的方法有t检验和F检验。

t检验可以用来判断截距和斜率的显著性，F检验可以用来判断模型整体的显著性。

总结：线性回归分析是一种常用的数据分析方法，可以用于研究两个变量之间的线性关系。

通过收集数据，建立模型，估计参数和进行拟合优度评估，我们可以获得对变量之间关系的深入认识。

同时，我们还可以通过检验模型的显著性来判断模型的可靠性。

经济计量学第二讲 双变量回归模型及其估计问题


东北财经大学数量经济系
第四节 两个说明性例子
第四节 两个说明性例子
例一：1970-1980年间美国的咖啡消费 例二：利用1980-1991年数据建立的美国
凯恩斯消费函数
东北财经大学数量经济系
东北财经大学数量经济系
第三节
双变量回归模型的估计问题（2）
2 ˆ 2 ˆ (Y Y ) u
2 ˆ ˆ (Y b 1 b 2 X )
min
ˆ2 u ˆ b 1 ˆ2 u ˆ b 2
ˆ ˆ 2 (Y b 1 b 2 X ) 0
ˆ ˆ 2 ( Y b 1 b 2 X )( X ) 0
密 度 true
ˆ b2 d
东北财经大学数量经济系
b2
ˆ b2 + d
ˆ b2
第三节
双变量回归模型的估计问题（11）
五、判定系数r2:“拟合优度”的度量
（一）判定系数的意义 1.判定系数R2的含义 2.文图或巴伦坦图
东北财经大学数量经济系
第三节
双变量回归模型的估计问题（12）
（二）判定系数R2的计算 1.总平方和（TSS）的计算及分解 2.判定系数R2的计算公式 3.判定系数R2与相关系数的关系 4.相关系数r 的性质
ˆ ˆ b1 Y b 2 X
东北财经大学数量经济系
第三节
数值性质
双变量回归模型的估计问题（5）
是指由于运用最小二乘法而得以成立的那 些性质而不管数据是如何产生的。
统计性质
是指仅在数据产生的方式满足一定的假设 下才得以成立的那些性质。
数 值 性 质
1.OLS估计量是纯粹由可观测的量表达式，是容易计算的； 2.OLS估计量是点估计量； 3.一旦从样本数据得到OLS估计值，便可画出样本回归线。

计量经济学ch2 双变量回归分析

Ch2 双变量回归分析: 基本概念总体：研究对象的全体，总体的基本单位称为个体。

同一对象的度量数据集合，也成为总体。

样本：总体中若干个体的集合。

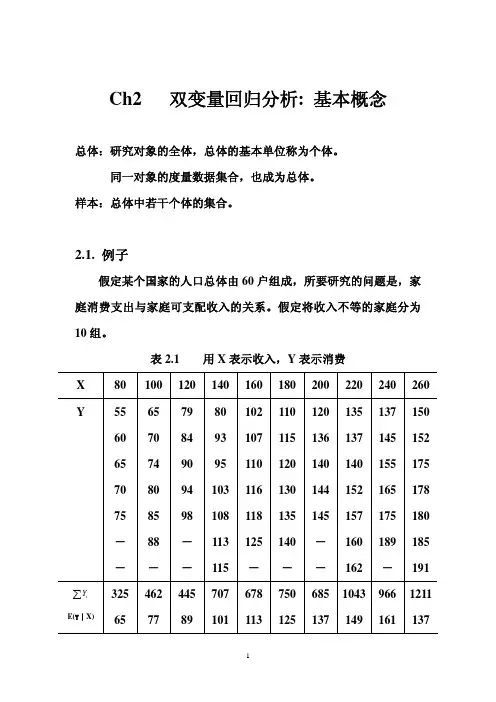
2.1. 例子假定某个国家的人口总体由60户组成，所要研究的问题是，家庭消费支出与家庭可支配收入的关系。

假定将收入不等的家庭分为10组。

表2.1 用X 表示收入，Y 表示消费X80 100 120 140 160 180 200 220 240 260Y 55 65 79 80 102 110 120 135 137 150 60 70 84 93 107 115 136 137 145 152 65 74 90 95 110 120 140 140 155 175 70 80 94 103 116 130 144 152 165 178 75 85 98 108 118 135 145 157 175 180 － 88 － 113 125 140 － 160 189 185－－ － 115 － － －162－191iY ∑E(Y︱X)325 65462 77445 89707 101678 113750 125685 1371043 149966 1611211137条件概率与条件期望。

p(Y=60/X=80)=1/5p(Y=65/X=80)=1/5，p(Y=70/X=80)=1/5 p(Y=75/X=80)=1/5进而根据条件概率，我们可计算条件期望（均值），即1()55(1/5)60(1/5)65(1/5)70(1/5)75(1/5)65E Y X X ==++++=图2.1 总体回归直线对应X 的不同水平，Y 的条件期望（均值）的变化，由于Y 的条件均值是对于给定X 的值而对于相应的所有Y 的值求条件均值，因此称为总体回归直线（PRL ）。

2.2. PRL 函数Y 的条件均值为函数，因此将Y 的条件均值表述为i X )()(i i X f X Y E = （2.1）称（2.1）为双变量总体回归函数。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
mediocrity
• The height of the children of unusually tall or unusually short parents tends to move toward the average height of the population.
3
• 回归的现代含义：
13
再次强调数据的质量
• Because of all these and many other problems, the researcher should always keep in mind that the results of research are only as good as the quality of the data.
6
几个例子
• 1. Reconsider Galton’s law of universal regression.
• In the modern view our concern is finding out how the average height of sons changes given the fathers’ height.
问题：能从一次抽样中获得总体的近似的 信息吗？如果可以，如何从抽样中获得总 体的近似信息？
30
31
32
画两条样本回归线尽可能拟合这些散点
33

• 图中直线（曲线）称为样本回归线 • 在总体回归函数（总固体回归线）不知情的情况
下，无法判断哪一条样本线能代表真实的总体线 • 姑且他们都能代表总体回归线 • 但因抽样波动，他们最多只是真实总体线的一个
• 不满意的结论，并不一定是模型不够优美 ，有时是数据质量问题。
14
二、回归分析的基本概念
• 总体回归函数（PRF） • 随机干扰项 • 样本回归函数（SRF）
15
总体回归函数
• 包含60个家庭的例子，分成10个子总体
16
• 子总体的均值，称为“条件均值”，E(Y | X)
17
• 每个子总体内，呈现一个分布 • 子总体的均值，随着收入增加而增加
4
深入理解
变量间的关系：
• 经济变量之间的关系，大体可分为两类：
• 确定性关系或函数关系：研究的是确定现象非随
机变量之间的关系。 • 例：圆面积＝ f ( , r)＝ r2
• 统计依赖关系：研究的是非确定现象随机变量间
的关系。
• 例：农作物产量＝f（气温，降雨量，阳光，施肥量等）
• 对变量间统计依赖关系的考察主要是通过相关分析 或回归分析来完成的
• 正是来自于理论上（或者假设）的因果关 系，才假设因变量依赖于自变量。而不是 相反。
11
几个术语：
12
• simple, or two-variable, regression analysis.
• 简单回归分析或者双变量回归分析，或单 元回归分析
• multiple regression analysis. • 多元回归分析
2）变量观测值的观测误差的影响；
3）模型关系的设定误差的影响；
4）其它随机因素的影响。
产生并设计随机误差项的主要原因：
1）理论的模糊性；
2）数据的欠缺；
3）核心变量和周边变量；
4）人类行为的内在随机性；
5）糟糕的替代变量；
6）节省原则；
7）错误的函数形式。
29
样本回归函数
总体的信息往往无法掌握，现实的情况只 能是在一次观测中得到总体的一个样本。
• 相关分析指线性相关分析。 • 不线性相关并不意味着不相关 • 相关分析对称地对待任何（两个）变量，两个变
量都被看作是随机的。 • 回归分析对变量的处理方法存在不对称性，即区
分因变量和解释变量：前者是随机变量，后者 不 是。
10
概念辨析：回归与因果关系
• 回归分析/相关分析研究一个变量对另一个 （些）变量的统计依赖关系，但它们并不意 味着一定有因果关系
21
• 含义：
回归函数（PRF）说明被解释变量Y的平均状态 （总体条件期望）随解释变量X变化的规律。
• 函数形式：
可以是线性或非线性的。 引例中，将消费支出看成是其可支配收入的线 性函数时：
22
“线性”的两种含义
• 对变量为线性：
Y的条件均值是Xi的线性函数
• 对参数为线性
Y的条件均值是 的线性函数
• In other words, our concern is with predicting the average height of sons knowing the height of their fathers.
7
年龄与身高
8
Phillips curve
9
概念辨析：回归分析与相关分析
计量经济学 Econometrics
孙坚强 Ph.D. in Finance jqsunmath@
1
双变量回归模型：基本概念
• 一、回归的含义 • 二、回归分析的基本概念
2
1、回归的含义
• “回归”的由来 Francis Galton, Karl Person：regression to
18
• 收入与消费支出的关系；收入与子总体均值的关系： • 图中的黑点表示不同X值下Y的条件均值 • 条件均值的连线称为总体回归线（总体回归曲线）
19
20
概念
• 在给定解释变量Xi条件下，被解释变量Yi的 期望轨迹称为总体回归线(PRL)，或更一般 地称为总体回归曲线。
• 相应的函数：
称为(双变量)总体回归函数(PRF)。
5
深入理解
• 回归分析是研究因变量对另一(些)解释变量的依赖关 系的计算方法和理论。
• 其用意：在于通过后者的已知或设定值，去估计和（ 或）预测前者的（总体）均值。
• 回归分析构成计量经济学的方法论基础，其主要内容 包括：
（1）根据样本观察值对经济计量模型参数进行估计，求 得回归方程；
（2）对回归方程、参数估计值进行显著性检验； （3）利用回归方程进行分析、评价及预测。
计量经济学中的线性回归模型（LRM）是指 参数为线性的情况，对解释变量可以是或者不 是线性的。
23
24
随机干扰项
25
例1.1中，个别家庭的消费支出为：
26
27
• 对总体回归函数的随机形式（随机设定形 式、单值形式）取条件期望：
28
随机误差项主要包括下列因素的影响：
1）在解释变量中被忽略的因素的影响；