当前位置：文档之家 › 第三章周期信号的傅里叶级数表

第三章周期信号的傅里叶级数表

  • 格式：ppt
  • 大小：7.43 MB
  • 文档页数：117

下载文档原格式

  / 117

合集下载

3.2 周期信号的傅里叶级数分析

3.2 周期信号的傅里叶级数分析

f (t )
n
F e
n

jn1t
E T1
n1 jn1t Sa( 2 )e n

20
E f (t ) T1
n1 jn1t Sa( 2 )e n

E n1 Fn Sa( ) T1 2
2 E n1 cn Sa( ) T1 2 E c0 T1 n0
E cos(n t )dt
2 1 2

2E 2E n1 2 sin(n1t ) sin( ) T1n1 n 2 2

E1

n1 2 E n1 Sa( ) Sa( ) 2 T1 2
E 2 E f (t ) T1 T1
n1 Sa( 2 ) cos(n1t ) n 1
f1 t
f1 (t ) 1 f (t )
1
f (t)
练习P 3 7 171
2
－T

T T 0
2
T 2
T
2T
t
T 2
0 －1
T 2
T
2T
t
注意：不可左右移动，否则改变了 原信号的对称性。
11
四、傅里叶有限级数与最小方均误差
f (t ) a0 (an cos n1t bn sin n1t )
32
1 1 2 2 2 2 2 P a0 (an bn ) c0 cn 2 n 1 2 n 1 1 2 2 2 c0 (2 Fn 2 F n ) 2 n 1 c0 Fn F n
2 2 2 n 1 n 1 n
2 b2 T1

T1 2 T 1 2

《信号与系统》奥本海姆第三章

《信号与系统》奥本海姆第三章

周期性方波序列的频谱
N1 2 N 10
N1 2 N 20
k
k
N1 1 N 10
k
Generated by Foxit PDF Creator © Foxit Software For evaluation only.

x ( r )e
j
2 kr N
1 ak m
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
4. Paseval定理
DFS x(n) ak
成谐波关系的复指数信号集:
k (n) {e
j (k 2 )n N
}, k 0, 1, 2,...
公共周期为N，集合中只有 N 个信号是彼此独立。 一个周期为N的序列有：
x[ n ] ak e
k j(k 2 )n N

k N

ak e
j (k
2 )n N
,其中 k 为N个相连的整数
2 rn N
N ar
1 N
即
1 ar N
2 rn N

n N
n N

x ( n ) e jr 0 n , 0
2 N
一个周期为N的序列有：
x(n)
ak 1 N
k N

ak e
j
2 kn N
DFS
j 2 kn N
n N
Wang Zhengyong
Generated by Foxit PDF Creator © Foxit Software For evaluation only.

3-1周期信号的傅里叶级数

3-1周期信号的傅里叶级数

iii) bn
f (t ),sin n1t sin n1t ,sin n1t

t0 T1
t0
f (t ) sin n1tdt T1 2
哈尔滨工业大学自动化测试与控制系
信号与系统—signals and systems
2．对于周期函数 f (t ) ，由于 a0 , a n , bn积分值与积 分区间起始点无关(只要积分区间大小为T1)，故在 t , f (t ) 均可以展成傅立叶级数
E T1
n

01
2
4



0
2
4



2 谱线间隔 1 ( ) T1 2 零值点频率
哈尔滨工业大学自动化测试与控制系
信号与系统—signals and systems
指数形式：f t
n


Fn e jn1t
n1 jn1t Sa( 2 )e n
常用完备正交函数集： i)三角函数集： 2 sin 0t ,sin 20t ,,1, cos 0t , cos 20t , (t0 , t0 ) 0 ii)复指数函数集：1, e j0t , e j0t , e j 20t , e j 20t ,
f(t)=C1 sin w1t+C3 sin w3 t+C6 sin w6 t
c2k 1 cos[(2k 1)1t 2k 1 ]
vii)偶次谐波分量：2 f1 , 4 f1 , 6 f1 , ... 对应的
c2 k cos(2k1t 2 k )
viii)直流分量：c0
哈尔滨工业大学自动化测试与控制系
信号与系统—signals and systems

信号与系统第6讲第3章周期信号的傅里叶级数表示

信号与系统第6讲第3章周期信号的傅里叶级数表示

sin(2 k(1/ 4)) k
sin(k k
/ 2)
根据Example3.5的结果，用性质计算傅里叶级数的系数
分析：原函数为x(t),本函数为g(t)
g (t )
x(t
1)
1 2
,周期方波的参数T
4,T1
1,
如果原函数的系数为ak，x(t 1)的系数为bk
bk
a e jk (2 / 4)1 k
在不连续点上，傅里叶级数的收敛趋势-吉伯斯现象
不连续点上收敛于不连续点的平均值 不连续点附近呈现起伏现象，起伏的峰值不随N增加而降低 峰值为不连续点差值的9%
吉伯斯现象的实际意义
不连续信号的傅里叶级数截断近似在接近不连续点有高频起伏 选择足够大的N，可以保证这些起伏的总能量可以忽略
2024/6/10
2024/6/10
信号与系统－第6讲
19
§3.5 连续时间傅里叶级数性质
（4）Example3.8 计算周期冲激串的傅里叶级数系数 根据性质计算周期方波的系数
周期冲激串可表示为x(t) (t kT ) k
ak
1 T
T / 2 (t)e jk 2t /T dt 1
T / 2
T
周期方波为g (t ),它的导数为q(t )
c0为直流分量， c0 2T1 / T
对照前面 例题验证
结果
20
§3.5 连续时间傅里叶级数性质
（5）Example3.9
1.x(t)是实信号
2.x(t)是周期信号，T 4，傅里叶级数系数ak
3.ak 0，k 1
4.傅里叶系数为bk
e
j
k
/
2
a
的信号是奇信号

周期信号的傅里叶级数表

周期信号的傅里叶级数表
17
分量e j0t 可表示为
1
0
cos 0t
1 2
(e
j0t
e
j0tபைடு நூலகம்
)
表示为
1
1
2
2
0 0 0
因此，当把周期信号 x(t)表示为傅里叶级数
x(t) ake jk0t时，就可以将 x(t) 表示为 k
a1a0 a1
a3a2
a2 a3
0 0
这样绘出的图
称为频谱图
18
频谱图其实就是将 a随k 频率的分布表示出来，
14
有 x(t) ake jk0t , k 0, 1, 2
k
显然 x(也t)是以
为2周 期的。该级数就是傅里叶级
0
数， 称为a傅k 立叶级数的系数。
这表明用傅里叶级数可以表示连续时间周期信号，
即: 连续时间周期信号可以分解成无数多个复指数谐 波分量。
例1：
x(t)
cos 0t
1 e j0t 2
6
3.1历史的回顾 （A Historical Perspective）
任何科学理论, 科学方法的建立都是经过许多人 不懈的努力而得来的, 其中有争论, 还有人为之献 出了生命。历史的经验告诉我们, 要想在科学的 领域有所建树，必须倾心尽力为之奋斗。今天我 们将要学习的傅立叶分析法，也经历了曲折漫长 的发展过程，刚刚发布这一理论时，有人反对， 也有人认为不可思议。但在今天，这一分析方法 在许多领域已发挥了巨大的作用。
即： x(t) akeskt
k
同理： x(n)
ak
Z
n k
k
y(t) ak H (sk )eskt
k

第3章傅里叶级数

第3章傅里叶级数

同频率
cos(t )
LTI
A cos(t )
LTI系统对正弦信号的响应仍然是同频正弦信号
本书由天疯上传于世界工厂网-下载中心
复指数信号激励LTI系统的情况。
e
st
LTI
?
s ( t )
y(t ) h(t ) * e h( )e
st
d
e
st



x(t )
a0 1
k 3
a e
k
3
jk 2t
a1 a1 1 / 4
a3 a3 1 / 3
a2 a2 1 / 2
本书由天疯上传于世界工厂网-下载中心
解：
1 j 2t j 2t x(t ) 1 (e e ) 4 1 j 4t 1 j 6t j 4t j 6t (e e ) (e e ) 2 3
sincossincossincos322傅里叶级数系数的确定正交函数集t的周期函数正交函数集的概念一个以t为周期的周期函数在一段长度为t的区间上的积分与起始位置无关jkdtsincostdttdt正弦波的上波瓣和下波瓣的面积相等对于高次谐波而言无非是在一个周期之内上对于高次谐波而言无非是在一个周期之内上波瓣和下波瓣多了一些但是上波瓣的总面积和波瓣和下波瓣多了一些但是上波瓣的总面积和下波瓣的总面积还是相等的下波瓣的总面积还是相等的sincosjkdt构成了一个正交函数集
周期函数的一个基本性质。
x(t ) x(t T )

T a
a
x(t )dt x(t )dt
a
T
T a
T
x(t )dt

奥本海姆《信号与系统》配套题库【课后习题】(周期信号的傅里叶级数表示)

第3章周期信号的傅里叶级数表示基本题3.1 有一实值连续时间周期信号x（t），其基波周期了T＝8，x（t）的非零傅里叶级数系数为a1＝a－1＝2，a3＝a－3＝4j。

试将x（t）表示成：解：3.2 有一实值离散时间周期信号x[n]，其基波周期N＝5，x[n]的非零傅里叶级数系数为，试将x[n]表示成：解：3.3 对下面连续时间周期信号求基波频率ω0和傅里叶级数系数a k，以表示成解：即非零的傅里叶级数系数为3.4 利用傅里叶级数分析式计算下连续时间周期信号（基波频率ω0＝π）的系数a k：解：因ω0＝π，故3.5 设x1（t）是一连续时间周期信号，其基波频率为叫ω1，傅里叶系数为a k，已知x2（t）＝x1（1－t）十x1（t－1），问x2（t）的基波频率ω2与ω1是什么关系？求x2（t）的傅里叶级数系数b k与系数a k之间的关系。

解：x1（1－t）和x1（t－1）的基波频率都是ω1，则它们的基波周期都是T1＝2π/π。

因为x2（t）是x1（1－t）和x1（t－1）的线性组合，所以x2（t）的基波周期，即ω2＝ω1。

又故即3.6 有三个连续时间周期信号，其傅里叶级数表示如下：利用傅里叶级数性质回答下列问题：（a）三个信号中哪些是实值的？（b）哪些又是偶函数？解：（a）与式对照可知，对于x1（t），有由共轭对称性可知，若x1（t）为实信号，则有显然故x1（t）不是实信号。

同理，对于x2（t），对于x3（t），由于故可知x2（t）和x3（t）都是实信号。

（b）由于偶函数的傅里叶级数是偶函数，由上可知，只有x2（t）的a k是偶函数，故只有x2（t）是偶信号。

3.7 假定周期信号x（t）有基波周期为T，傅里叶系数为，的傅里叶级数系数为b k。

已知，试利用傅里叶级数的性质求a k用b k和T表达的表达式。

解：当k＝0时，故3.8 现对一信号给出如下信息：（1）x（t）是实的且为奇函数；（2）x（t）是周期的，周期T＝2，傅里叶级数为a k；（3）对|k|>1，a k＝0；（4）试确定两个不同的信号都满足这些条件。

周期信号的傅里叶级数表


傅里叶级数与复变函数的关系
傅里叶级数可以看作是复数域中的三角函数，即复数域中的正弦和余弦。在复数域中，正弦和余弦函数表现为复指数函数的 形式。
复数的使用使得傅里叶级数的系数可以表示为实数，从而简化了计算。此外，复数的共轭也提供了相位信息，这在信号处理 中非常重要。
傅里叶级数与小波分析的关系
小波分析是傅里叶分析的进一步发展，它提供了更灵活的时频分析工具。小波变 换可以看作是傅里叶变换的一种扩展，它允许我们在不同的频率段使用不同的基 本函数。
三角函数形式
傅里叶级数的另一种表示形式，利用三角函数来表示周期信号。
傅里叶级数的三角函数形式
01
02
03
正弦形式
余弦形式
系数
傅里叶级数的正弦函数形式，用 于表示只包含正弦波的周期信号。
傅里叶级数的余弦函数形式，用 于表示只包含余弦波的周期信号。
在傅里叶级数中，每个正弦或余 弦函数都对应一个系数，表示该 函数在周期信号中的贡献程度。
03
傅里叶级数的性质
傅里叶级数的收敛性
傅里叶级数在数学上具有收敛性，意味着它可以将一个 周期函数表示为无穷级数，每个项都是正弦或余弦函数。
收敛的速度取决于函数的特性，例如，对于具有快速衰 减的周期函数，傅里叶级数收敛得更快。
傅里叶级数的对称性
傅里叶级数的对称性质是指，对于一个周期函数，其傅里叶级数的正弦和余弦项具有对称性。 这意味着，对于一个给定的周期函数，其傅里叶级数的正弦和余弦项的系数是相同的。
周期信号的傅里叶级 数表
目录
• 傅里叶级数简介 • 周期信号的傅里叶级数表示 • 傅里叶级数的性质 • 傅里叶级数的应用实例 • 傅里叶级数与其他数学工具的关系
01

信号与系统 第三章 周期信号的傅里叶级数展开

1 T
2 n 2

T1
f (t ) dt

F ( n1 )
左边是周期信号f(t)在一个周期里的平均功率（即单位时间内的能量）
2 2 1 1 2 jnt F ( n ) e dt F ( n ) dt F ( n ) 而同时有 T 1 1 1 T1 1 T1 T1
n 1
——余弦形式
x(t ) d 0 d n sin( n1t n )
n 1
——正弦形式
(1). f (t ) a0 an cosnt bn sin nt
n1

三角函数形式
(2). f (t ) A0 An cos(nt n )
而无物理意义。将来可以看出，指数函数形式比正弦函数形式在数 学上处理起来要方便的多。
§3.2 周期矩形脉冲的谱线特点
x(t )
E

T1

t
2 2
T1
脉冲为 ，脉冲高度为E，周期为T1
1 21 1 E 1 jn1t jn1t 2 X (n1 ) T1 x(t )e dt E e dt e jn1t T1 2 T1 2 T1 jn1 jn jn 1 2E 1 1 2 2 e sin(n1 ) e jn1T1 2 n1T1 sin(n1 ) E E 2 Sa (n1 ) T1 n T1 2 1 2
电子信息与电气工程学院
本章内容
连续时间周期信号的傅立叶级数表示 周期矩形脉冲的谱线特点
§3.1 连续时间周期信号的傅立叶级数表示
{1, cos n1t ,sin n1t} n=1,2, , 是一个完备的正交函数集

典型周期信号的傅里叶级数


三周期三角脉冲信号的傅里叶级数求解
周期三角脉冲信号，是偶函数。 f (t ) 解： 它是偶函数 E
bn 0
T1 2 T1 2
0
t
可求出傅里叶级数的系数a0,an, 留给同学们做。
其傅里叶级数表达式为： E 4E 1 1 f (t ) 2 cos( w1t ) cos(3w1t ) cos(5w1t ) 2 9 25 E 4E 1 n 2 2 sin 2 ( ) cos( nw1t ) 2 n 1 n 2 此信号的频谱只包含直流、基波及奇次谐波分量，谐波的幅度 以1/n2的规律收敛。
五、周期全波余弦信号的傅里叶级数求解
周期全波余弦信号，是偶函数。 解：令余弦信号为 f (t )
E
2 f1 (t ) E cos( w0t ) w0 T0 则，全波余弦信号为：
T 10 T1 2
T1 2
T1
t
f (t ) f1 (t ) E cos( w0t )
其傅里叶级数表达式为： 2E 4E 1 1 1 f (t ) cos( 2w1t ) cos( 4w1t ) cos(6w1t ) 3 15 35 2E 4E 1 (1) n 1 2 cos( 2nw0t ) n 1 4n 1 此信号的频谱只包含直流、基波及偶次谐波分量，谐波的幅度 以1/n2的规律收敛。

cos(n1t )
（2）周期矩形脉冲信号的幅度、相位谱
1 周期矩形脉冲信号的幅度频谱中收敛规律为 , n为其频带宽度B B , Bf
E T1
Cn
n

2

4

nw1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
周期信号都可用正弦 函数级数表示” • 1829年狄里赫利第 一个给出收敛条件 • 拉格朗日反对发表 • 1822年首次发表 “热的分析理论”
4
傅里叶的两个最主要的贡献——
• “周期信号都可表示为成谐波关系的 正弦信号的加权和”——傅里叶的第 一个主要论点
• “非周期信号都可用正弦信号的加权 积分表示” ——傅里叶的第二个主要论点
5
§3.2 LTI系统对复指数信号的响应 The Response of LTI Systems to
Complex Exponentials
一个LTI系统对复指数信号的响应也是 同样一个复指数信号，不同的只是在幅度 上的变化，即：
连续时间信号：est H sest 离散时间信号：zn H zzn
第三章 周期信号的傅里叶级数表示
FOURIER SERIES REPRESENTATION OF
PERIODIC SIGNALS
主要内容： Ⅰ.周期信号的频域分析 Ⅱ.傅里叶级数的性质 Ⅲ.LTI系统的频域分析
1
§3.0 引言 Introduction
时域分析方法的基础 ： 1) 信号在时域的分解 2) LTI系统满足线性、时不变性
x t
ak e jk0t
a e jk (2 /T )t k
k
k
2 它也是以 ? 0 为周期
该级数就是傅里叶级数，这表明用傅里叶级数 可以表示连续时间周期信号。即: 连续时间周 期信号可以分解成无数多个谐波分量。
16
图形见下页
17
18
二 频谱的概念
2
2
2
2
cos4t 3 cos7t 3
11
12

同理： x n ak zk n k 则： yn ak H zk zk n k
13
• 综上：对于连续时间和离散时间来说，如
果一个LTI系统的输入能够表示成复指数的
线性组合，那么系统的输出也能够表示成
2
ak

1 4
Sa k
4

ak

1 8
Sa k
8

3）谱线随参数变化的结论：
ak

2T1 T0
Sak0T1
2T1 T0
Sa k
2
T0
T1

T1 不变 T0
T1 T0

谱线间隔
0

2
T0
变小
幅度下降 2T1
T0
频谱包络形状不变，0点频率不变
0t
2
5 limSa t 0 t
sin t dt t
1. 矩形脉冲频谱分析
ak

2T1 T0
Sak0T1
2T1 T0
Sa k
2
T0
T1


谱线为离散的（谐波性），在


k0

k
2
T0
时取值，
脉冲周期越大，谱线间隔 0 越小，越密；
8
复指数函数 est 、z n 是一切LTI系统的
特征函数。同时:

H s htestdt t

H z hnzn n
分别是LTI系统与复指数信号相对应的特征 值。只有复指数函数才能成为一切LTI系统 的特征函数。
例题3.1
9
例3.1 已知系统的输入输出关系为 yt xt 3，求：
T
。这种频谱常称为离散频谱。
该系统的特征函数，且特征值为1。
解：
h(t) (t T ) ， x(t) x(t T ) 。
如果 x(t) 是系统的特征函数，且特征值为 1，则应有：
y(t) x(t)*h(t) x(t T ) x(t) 1

满足这一要求的冲激序列为 x(t) (t kT ) 。 k
2 T0
T1

1）设矩形脉冲的高度不变，脉冲宽度 2T1 不变，周期 T0 增
大时，具体看频谱如何变化？
T1 1 , T0 4
ak

2T1 T0
Sa k
2
T0
T1


1 2
Sa k

2

k k 2 为第一个零点，对应
2

k0
2 T0
T1


1 8
Sa k
8

k k 8 为第一个零点，对应 8
k0 80 ,0 2 T0
ak

2T1 T0
Sak0T1
2T1 T0
Sa k
2 T0
T1

ak

1 2
Sa k

2

ak
22
2
2
2
2
1 e j7t 1 H j7 e j7t 1 e e j21 j7t , 1 e j7t 1 H j7 e j7t 1 e ej21 j7t
22
2
2
2
2
由叠加原理

y2 t
1 e e j12 j4t 1 e e j12 j4t 1 e e j 21 j7t 1 e e j 21 j7t

20 ,0

2
T0
T1 1 , T0 8
ak

2T1 T0
Sa k
2
T0
T1


1 4
Sa k

4

k k 4 为第一个零点，对应4Βιβλιοθήκη k040 ,0

2
T0
T1 1 , T0 16
ak

2T1 T0
Sa k
21
~
22
23
24
——傅里叶级数的另一种三角函数形式
25
四 连续时间傅里叶级数的系数确定
26
在确定上述积分时，只要积分区间是一个周期即可， 对积分区间的起止并无特别要求，因此可表示为：
27


x(t)
a k e jk0t
a e jk(2 T )t k
k
k
① x1t e j2t时，系统的输出 y1t ; ② x2 t cos4t 3 cos7t 3！时，系统的输出 y2 t 。
分析：复指数输入为LTI系统的特征函数，根据 yt H sest
只需求出系统的特征值 H s,即可求出①的输出。
解：① x1t e j2t s j2
Sa K

2
T0
T1


Sa

K0T1


sin K0T K0T
为抽样函数
抽样函数
抽样函数的性质:
1 Sa t Sa t
2 lim Sa t 1 t 0
3 Sa t 0,
t n ,
n 1, 2, 3
4
sin t dt ,
在傅里叶级数中，各个信号分量（谐波 分量） 间的区别也仅仅是幅度（可以是复数） 和频率不同。因此，可以用一根线段来表示 某个分量的幅度，线段的位置表示相应的频 率。
即：
代表
一根线段
某个分量的幅度
线段的位置 代表 相应的频率
19
20
因此，当把周期信号表示成傅里叶级数时，
x t ake jk0t k
k0 40 , 0 2 T0
T1 1 T0 16
ak

2T1 T0
Sa k
2
T0
T1


1 8
Sa k

8

k k 8 为第一个零点，对应 8
k0 80 ,0 2 T0
ak

1 2
Sa k
ak

1 T
x(t)e jk0tdt 1
T
T
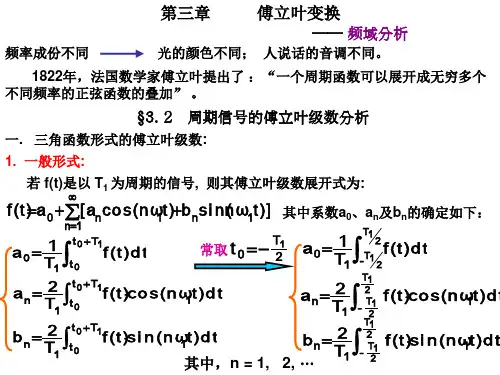
x(t)e jk(2 T )tdt
T
28
29
解：方法一：直接利用公式进行求解
ak

1 T
x(t)e jk0t dt 1
T
T
x(t)e jk(2 T )t dt
T
方法二：


x(t)
a k e jk0t
T0 不变 T1
T1 T0
主瓣内包含的谐波分量数增加
谱线间隔不变 幅度下降 2T1
T0
0

2
T0
频谱的包络改变，0点频率变化
主瓣内包含的谐波数量也增加
周期性矩形脉冲信号的频谱特征： 1. 离散性 2. 谐波性 3. 收敛性
(1)离散性——谱线是离散的而不是连续的，谱线之间
的间隔为
0

2
7
补充例题：
例:对单位冲激响应 h(t) (t) 的LTI系统，其特征函数，
相应的特征值是什么?
解： h(t) (t) 的 LTI 系统是恒等系统，所以任何函 数都是它的特征函数，其特征值为 1。
例:如果一个LTI系统的单位冲激响应为，h(t) (t T)
找出一个信号，该信号不具有 est 的形式，但却是
2
T0
T1


1 2
Sa k

2

k k 2 为第一个零点，对应 2
k0 20 ,0 2 T0
T1