当前位置：文档之家 › 傅里叶变换(周期和非周期信号)

傅里叶变换(周期和非周期信号)

  • 格式：ppt
  • 大小：1.24 MB
  • 文档页数：70

下载文档原格式

  / 70

合集下载

4种傅里叶变换

4种傅里叶变换

copyright©赵越 ise_zhaoy1@
4种傅里叶变换
DFT的变换 的变换
x(nT)=x(n)
Tp = 1 F
Tp = NT
x(e jkΩ0T ) x(k)
0 T 2T 1 2
Ωs = 2 π T 1 fs = T
NT
N
Ω0 =
2 π =2 F π Tp
t n
Ωs = N 0 Ω
( )
--Ω
copyright©赵越 ise_zhaoy1@
4种傅里叶变换
4.离散傅里叶变换 离散傅里叶变换(DFT) 离散傅里叶变换
周期性离散时间信号从上可以推断： 周期性离散时间信号从上可以推断： 从上可以推断 周期性时间信号可以产生频谱是离散的 离散时间信号可以产生频谱是周期性的。 离散时间信号可以产生频谱是周期性的。 得出其频谱为周期性离散的 得出其频谱为周期性离散的。 周期性离散
copyright©赵越 ise_zhaoy1@
4种傅里叶变换
四种傅里叶变换形式的归纳
copyright©赵越 ise_zhaoy1@
Ω
正: X(e jω ) =
1 反 : x(n) = 2π
n=−∞
x(n)e − jnω ∑
∞
∫π
−
π
X(e jπ )e jnω dω
copyright©赵越 ise_zhaoy1@
4种傅里叶变换
对称性
时域信号 离散的 非周期的 频域信号 周期的 连续的
时域：非周期、离散（取样间隔为T 时域：非周期、离散（取样间隔为T） 频域：连续、周期（ 频域：连续、周期（周期为 Ω = 2π ） s
copyright©赵越 ise_zhaoy1@

2.5信号的频域分析(非周期信号)2.6傅立叶变换的性质

2.5信号的频域分析(非周期信号)2.6傅立叶变换的性质

能 量 谱
由此最后得
E = ∫ x2 (t )dt =
−∞ ∞
1 ∞ 2 X(ω) dω 2π ∫−∞
(16)
式（15）亦称巴塞伐尔方程或 能量等式。它表示，一个非周 期信号x(t)在时域中的能量可由 它在频域中连续频谱的能量来 表示。 式（15）亦可写成
E= 1 ∞ 2 X(ω) dω 2π ∫−∞ 1 ∞ 2 = ∫ X(ω) dω = ∫ S(ω)dω
证明： 由欧拉公式
X (ω) = ∫ x(t)e
−∞
∞ −∞
∞
− jωt
dt
∞ −∞
X (ω) = ∫ x(t) cosωtdt − j∫ x(t) sin ωtdt
= Re X (ω) + j Im X (ω)
若x(t)为实函数
Re X (ω) = Re X (−ω) Im X (ω) = − Im X (−ω)
x(t) = Arect
(t − t0 )
T
图2.30 具有时移t0的矩形脉冲
X( f ) = AT sin c(πfT) sin c(πfT) > 0 − 2πt0 f , ϕ( f ) = − 2πt0 f ±π , sin c(πfT) < 0
测试技术
2.6傅里叶变换的性质 2.6傅里叶变换的性质
∫
∞
−∞
x(t) dt < ∞
但上述条件并非必要条件 必要条件。因为当引入广义函数概 必要条件 念之后，许多原本不满足绝对可积条件的函数也能进行傅 里叶变换。 若将上述变换公式中的角频率ω用频率f来替代，则由 于ω=2πf，式（5）和（6）分别变为
X( f ) = ∫ x(t)e− j 2πft dt

第3章 连续信号的频谱——傅里叶变换

第3章 连续信号的频谱——傅里叶变换

• 直到19世纪末，制造出电容器。20世纪初，谐振电路、滤波
器、正弦振荡器等一系列问题的解决为正弦函数与傅里叶分 析的在通信系统中的应用开辟了广阔的前景。 • 从此，在通信与控制系统的理论研究和实际应用之中，采用 频率域（频域）的分析方法比经典的时间域（时域）方法有 许多突出的优点。 • 当今，傅里叶分析方法已成为信号分析与系统设计不可缺少 的重要工具。 • 20世纪70年代，出现的各种二值正交函数（沃尔什函数）， 它对通信、数字信号处理等技术领域的研究提供了多种途径 和手段。使人们认识到傅里叶分析不是信息科学与技术领域 中唯一的变换域方法。
nw1 nw1

0
w
nw1
w1 0 w1
nw1
w
正、负频率相应项成对合并，才是实际频谱函数。
4.周期信号的功率特性
—时域和频域能量守恒定理
周期信号的平均功率P：在一个周期内求平方再求积分。
1 t0 T1 2 f (t )dt P f (t ) t T1 0 1 1 2 2 2 2 2 a0 ( an bn ) c0 cn 2 n 1 2 n 1
其傅里叶级数三角展开式中 仅含基波和奇次谐波
例子
例如：奇谐函数
f (t )
E 2
T1 2
f (t )
E 2
T 1 2
0
E 2
T1 2
t
0
E 2
T1 2
t
sin( w1t )
E 2
f (t )
E 2
T1 2 T 1 2 T1 2
f (t )
0
E 2
t

0
E 2
T1 2

第七3章 非周期信号的傅里叶变换

第七3章 非周期信号的傅里叶变换

则
G( ) g (t )e jt dt 2 Ee jt dt
2

13
7-5典型信号的傅立叶变换
E sin 2 E Sa ( ) 2 2

表明单个门函数的傅立叶变换是一个抽样函数。 n ( n 1, 2, ) Sa ( )0 。 当 时， 2 2 2 n 1 G ( ) 取 ， 的第一个零点的频率为 c ， 定义 0 ~ c （或者 0 ~ fc ）之间的频率范围称为信号宽度。
这是傅立叶变换存在的充分条件，而不是必要条件， 因为有些不满足绝对可积条件的信号，但当引入了冲激函 数 ( ) 之后，就可以大大地扩展傅立叶变换的范围。
12
7-5典型信号的傅立叶变换
1 单个门函数 g (t )
g(t)
E


2
0

2
t
单个门函数
其幅度为E，宽度为

， F[ g (t )] G( )，
• 原来的离散量 n1 演变成连续量 。
• 离散求和 运算 变成连续积分
运算
，即
（ 1）
（2 ）
F ( )
1 f (t ) 2


f (t )e jt dt
F ( )e jt d



式（1）（2）是一对傅立叶变换对，式（2）称为非周 期信号 f (t ) 的傅立叶正变换或称为频谱密度函数.
2 ，用指数形式傅立 T 为周期，脉宽为 ，基频为 1 T 叶级数展开可得
1 T Fn 2T fT (t )e jn1t dt T 2
1 2 E jn1t Ee dt T 2 T

傅里叶变换公式

傅里叶变换公式

连续时间周期信号傅里叶级数：⎰=T dt t x Ta )(1⎰⎰--==T tTjkT tjk k dt et x Tdt et x Ta πω2)(1)(1离散时间周期信号傅里叶级数：[][]()∑∑=-=-==Nn nN jk Nn njkwk e n x Ne n x Na /2110π连续时间非周期信号的傅里叶变换：()⎰∞∞--=dt e t x jw Xjwt )(连续时间非周期信号的傅里叶反变换：()dw e jw X t x jwt ⎰∞∞-=π21)(连续时间周期信号傅里叶变换：∑+∞-∞=⎪⎪⎭⎫⎝⎛-=k k kw a jw X T 22)(πδπ连续时间周期信号傅里叶反变换：()dw e w w t x jwt ⎰∞∞--=0221)(πδπ离散时间非周期信号傅里叶变换：∑∞-∞=-=nnj e n x eX ωωj ][)(离散时间非周期信号傅里叶反变换：⎰=π2d e )(e π21][ωωωn j j X n x离散时间周期信号傅里叶变换：∑+∞-∞=-=kk k a X )(π2)e (0j ωωδω离散时间周期信号傅里叶反变换：[]ωωωδωd e n n j ⎰--=π20πl)2(π2π21][x拉普拉斯变换：()dt e t s Xst -∞∞-⎰=)(x拉普拉斯反变换：()()s j21t x j j d e s X st ⎰∞+∞-=σσπZ 变换：∑∞-∞=-=nnz n x X ][)z (Z 反变换： ⎰⎰-==z z z X r z X n x n nd )(πj21d )e ()(π21][1j π2ωω。

信号与系统第3章傅里叶变换

信号与系统第3章傅里叶变换

sin( k n) x k n
0(k , n 1,2,3,..., k n)
2．级数形式
周期f信 t,周 号期 T1,基 为波
在满足狄氏条件时，可展成
角 1频 2 T 1 率
为
f(t)a 0 a nco n s 1 tb nsin n 1 t 1 n 1
称为三角形式的傅里叶级数，其系数
3.1 引言
频域分析
从本章开始由时域转入变换域分析，首先讨论傅里叶变换。 傅里叶变换是在傅里叶级数正交函数展开的基础上发展而产生 的，这方面的问题也称为傅里叶分析（频域分析）。将信号进 行正交分解，即分解为三角函数或复指数函数的组合。
频域分析将时间变量变换成频率变量，揭示了信号内在的 频率特性以及信号时间特性与其频率特性之间的密切关系，从 而导出了信号的频谱、带宽以及滤波、调制和频分复用等重要 概念。
以上等式都可以通过计 算定积分来验证。
证明：
利用三角学中积化和差 的公式
cos kx cos nx＝1 cos(k n) x cos(k n) x
2 当k n时，有
cos kx cos nxdx 1 cos(k n) x cos(k n) xdx
2
1 2
sin( k n) x k n
cos nxdx 0(n 1,2,3,...)
sin nxdx 0(n 1,2,3,...)
sin kx cos nxdx 0(k , n 1,2,3,...)
cos kx cos nxdx 0(k , n 1,2,3,..., k n )
sin kx sin nxdx 0(k , n 1,2,3,..., k n )
条件2：在一周期内，极大值和极小值的数目应是有限个。

sa函数的傅里叶变换推导过程

sa函数的傅里叶变换推导过程

sa函数的傅里叶变换推导过程傅里叶变换是一种将时域信号转换为频域信号的数学工具，它在信号处理、图像处理等领域有广泛的应用。

傅里叶变换将一个连续信号分解成一系列的正弦和余弦函数的和，可以描述信号的频率和幅度信息。

其中，傅里叶变换的核心是计算信号的频谱，而信号的频谱可以由信号的自相关函数或互相关函数得到。

在推导傅里叶变换的过程中，我们首先需要熟悉复指数函数以及它的性质。

复指数函数的定义如下：e^(jωt) = cos(ωt) + jsin(ωt)其中，j是虚数单位，ω表示频率，t表示时间。

傅里叶变换的推导包括两个部分：傅里叶级数和傅里叶变换。

傅里叶级数适用于周期信号，而傅里叶变换适用于非周期信号。

在这里，我们以非周期信号的情况来推导傅里叶变换。

假设我们有一个连续时间域信号x(t)，它的傅里叶变换为X(ω)。

那么，傅里叶变换的定义可以表示为：X(ω) = ∫[x(t) * e^(-jωt)] dt其中，∫表示积分运算，x(t)*e^(-jωt)表示信号x(t)与复指数函数的乘积。

根据欧拉公式，复指数函数可以表示为：e^(-jωt) = cos(-ωt) + jsin(-ωt) = cos(ωt) - jsin(ωt)将其代入傅里叶变换的定义中，得到：X(ω) = ∫[x(t) * (cos(ωt) - jsin(ωt))] dt进一步展开，可以得到：X(ω) = ∫[x(t)cos(ωt)] dt –j∫[x(t)sin(ωt)] dt这样，我们可以将信号x(t)表示为正弦和余弦函数的和的形式：x(t) = (1/2π) ∫[X(ω)cos(ωt)] dω + (1/2π)∫[X(ω)sin(ωt)] dω这就是傅里叶级数的表达式，它将信号x(t)表示为一系列的正弦和余弦函数的和，其中X(ω)是信号的频谱。

接下来，我们将推导傅里叶变换的表达式。

首先，我们考虑连续时间的傅里叶级数表达式。

我们可以将频率ω看作连续变量，将级数变为积分，得到如下表达式：X(ω) = ∫[x(t)cos(ωt)] dt –j∫[x(t)sin(ωt)] dt然后，我们将上式中的正弦和余弦函数用正弦函数的复指数形式来替代，得到：X(ω) = ∫[x(t) * e^(-jωt)] dt这就是傅里叶变换的表达式。

信号与系统-3章_傅里叶变换

信号与系统-3章_傅里叶变换
t2t1
t2 t1
f(t)cos(n1t)dt,
t2 f(t)dt, n0
t1
n0
数
bnt1 t2t1 tf2s(tin )s2i(n n(n1t)1td)tdtt22 t1
t2 t1
f(t)sin(n1t)dt
或 f(t)a 2 0n 1(a nc o sn1 t b nsinn1 t)
-T0 O T0 2T0 t
f( t) n f1 ( t n T 0 ) n [A T A 0 ( t n T 0 ) ] [ u ( t n T 0 ) u ( t ( n 1 ) T 0 ) ]
将 f ( t ) 去除直流分量，则仅剩交流分量 f A C ( t )
t2
t1
cos(n1t)cos(m1t)dt 0

sin(n1t)sin(m1t)dt
0

,
mn
（2）“单位”常数性，即当 n 0 时，有
t1 t2 c o s 2 (n1 t)d tt1 t2 s in 2 (n1 t)d t T 2 t2 2 t1
f (t)
1

T

2
o
2
谱线间隔不变 2 π
TLeabharlann 1 Fn16示意图

T
t
幅值再减小一倍
o
2π


第一个过零点再增加一倍
结论
• 由大变小，Fn 第一过零点频率增大，即 2π/
所以 f 1/ 称为信号的带宽， 确定了带宽。 • 由大变小，频谱的幅度变小。 • 由于 T 不变，谱线间隔不变，即 2π/T不变。

非周期信号的傅里叶变换

非周期信号的傅里叶变换

0
a j a j a2 2
ℱ[sgn(t)]
2 j 2
2
j
哈尔滨工业大学自动化测试与控制系
信号与系统—signals and systems
4．阶跃函数
u(t) 1 1 sgn(t) 22
ℱ[u(t)] 1 2 1 2 1
2
2 j
j
F()
0
• u(t)含有直流分量，频谱中 含有冲激函数 • u(t)不是纯直流信号，频谱 中还出现其它频率分量
✓奇异信号的傅立叶变换 冲激信号、阶跃信号……
作业: 3-16(b)(c)，3-19
哈尔滨工业大学自动化测试与控制系
E
2 [cos(
)t cos(
)t]dt
0
0
sin( ) sin( )
E
2 E
2
cos
E[
2
cos
2
2 cos
]
E
(
)2
2
2
2E
cos
1
2
(
)
2
哈尔滨工业大学自动化测试与控制系
信号与系统—signals and systems
[例2]：求下列Bf
频谱第一个零点对应的频率
1
te jt
2
(
1
)2 e jt
2
2
e jt
j
0 j
0 j
1 j
1 j
Sa
2
(
)e
j
2
2
ii) B 2 , Bf 1
平移不会改变信号的频带宽度
哈尔滨工业大学自动化测试与控制系
信号与系统—signals and systems

傅里叶变换及反变换

傅里叶变换及反变换

物理意义：时域平移，对应频域相移，而幅频特性不变。
例： 求 (t - t 0 ) 的频谱。 (t t0 ) e jt0
(t-t0)
(1)
0 t0 t
|F(j)
1
0
φ()
0
7 时移特性： f (t t0 ) F ( j ) e j t0
时域平移，对应频域相移，幅频特性不变。
8 频移特性：
7 时移特性： f (t) F ( j ) 平移 f (t t0 ) F ( j ) e j t0
f (t) F ( j ) F ( j ) e j ( )
f (t t0 ) F ( j ) e jt0 F ( j ) e j ( )e jt0 F ( j ) e j ( )t0
F ( j ) Re[F ( j )] j Im[F ( j )] F *( j ) Re[F ( j )] j Im[F ( j )] 或者说，频谱的实部为偶函数，虚部为奇函数； 或者说，|F(j)|为偶函数，()为奇函数。
4 共轭特性
f (t) F ( j )，则 f * (t) F * ( j )
关于t
关于
证：若f (t)为偶函数，则 f (t) f (t)
F ( j ) f (t )e jtdt
F ( j ) f (t)e jtdt 令t
f ( )e j d f ( )e j d F ( j )
4 共轭特性
f (t) F ( j )，则 f * (t) F * ( j )
②：发生在一切频率上，是连续变化的；
③：各频率分量的系数 1 F ( j )d ，本身是无穷小量，
2
但F(jw)描述了各频率分量的相对关系，即描述了f(t)的频率特性；

周期信号的傅立叶变换

周期信号的傅立叶变换

− 2ω 1 − ω 1 o
ω 1 2ω 1
ω
− 2ω1 − ω1
o
ω1 2ω1
ω
δT (t ) 的频谱密度函数仍是冲激序列,强度和间隔都是 1。 ω
X
§3.6 连续时间系统的频域分析
一、频域的系统函数及频域分析
(对于LTI系统除了可以用第二章讲过的时域分析法外还可以用频域 分析法进行分析。它的基本原理是：将信号分解为无穷多项不同频 率的虚指数信号之和通过系统，最后进行响应的合成得到待求的响 应。时域分析与频域分析的关系如图)
1 、理想低通滤波器的系统函数 具有如图所示幅频、 具有如图所示幅频、相 频特性的系统称为理想 低通滤波器。 称为截 低通滤波器。ωc称为截 止角频率。 止角频率。
−ωc
1 H (ω )
0
ϕ (ω ) ωc
ωc
ω
−ωc
0
ω
H ( jω) = H (ω)e
e − jωt0 = 0
jϕ (ω )
§3.5周期信号的傅立叶变换
引言
周期信号： 周期信号：
f ( t ) ↔傅里叶级数F n
•
离散谱
非周期信号： 非周期信号：
f ( t ) ↔ 傅里叶变换F ( jω ) 连续谱
周期信号的傅里叶变换如何求？ 周期信号的傅里叶变换如何求？ 与傅里叶级数的关系？ 与傅里叶级数的关系？
X
一．一般周期信号的傅里叶变换 2π 设信号周期:T = ω1 由傅里叶级数的指数形式出发： 由傅里叶级数的指数形式出发： 其傅氏变换(用定义 其傅氏变换 用定义) 用定义
如
f (t) ↔ F( jω)
− jωt0
无失真传输时，Y ( jω) = KF( jω)e

傅里叶变换(周期和非周期信号)

傅里叶变换(周期和非周期信号)

例1的频谱图
周期信号的傅里叶变换——傅里叶级数
2、指数形式的傅里叶级数
式中，
f (t) Fne jn0t n
1
Fn T
T
2 T
f (t )e jn0tdt
2
证明
- n
傅里叶复系数
周期信号的傅里叶变换——傅里叶级数
2、指数形式的傅里叶级数
式中，
f (t) Fne jn0t n
1
Fn T
A
T1
2 A sin n1
n1 n
2
cos n1t
A
T1
2A sin
1
2
cos1t
A
sin
1
cos 21t
2A sin
3
31
2
cos 31t
......
2. 指数形式的傅里叶级数
周期矩形脉冲
f (t) Fne jn1t n
Fn
1 T1 A T1
T1
2 T1
f (t )e jn1tdt
2. T不变，τ减小，则频谱的幅度也将减小，谱线密度 保持不变，但包络过零点的间隔将增大。
A
F0 T
Back
非周期信号的傅立里叶变换
两个重要公式：
f ( t ) F( ) : F( ) f ( t )e jtdt
F( ) f (t ):
F -1F( ) f ( t ) 1 F( )e jtd
1、 三角函数式傅里叶级数
若周期函数 f (t) 满足狄里赫利（ Dirichlet）条件:
(1)在任意周期内存在有限个第一类间断点； (2)在任意周期内存在有限个的极值点； (3)在任意周期上是绝对可积的，即

信号分析基础(非周期信号频域分析)

信号分析基础(非周期信号频域分析)
1 jwt x x ( t) ( t) e dt ejwt dw 2

频谱函数（相当于原来的Cn）为：
x (t ) 1 X ( ) e j t d 2 x ( t ) e j t dt X ( )
非周期信号的频谱 5.傅立叶变换的主要性质
(1).奇偶虚实性
X( jf) x(t)ej2ftdt

x(t)cos 2 f tdt j x(t)sin 2 f tdt



R e X( jf) jI mX( jf)
a.若x(t)是实函数，则X(jƒ)是复函数； b.若x(t)为实偶函数，则ImX(jƒ)=0，而X(jƒ)是实偶函数，即 X(jƒ)= ReX(jƒ)； c.若x(t)为实奇函数，则ReX(jƒ)=0，而X(jƒ)是虚奇函数，即 X(jƒ)＝-j ImX(jƒ)； d.若x(t)为虚偶函数，则ImX(jƒ)=0，而X(jƒ)是虚偶函数； e.若x(t)为虚奇函数，则ReX(jƒ)=0，而X(jƒ)是实奇函数。
1 j n t 0 C x ( t ) e dt n T 2
频谱图： Cn
2 π 2 π
T 2 T 2
0
N为偶数
N为奇数
n
2 7π
-7ω 0
2 5π
-5ω 0
2 3π
2 3π
2 5π
2 7π
-3ω 0
-ω 0
0ω
0
3ω 0
5ω 0
7ω 0
ω
非周期信号的频谱
矩形脉冲函数的频谱
S (t)
单 位 面 积 ＝ 1
lim S t) ( t) (

傅里叶变换的基本性质

傅里叶变换的基本性质

傅里叶变换的基本性质（一）傅里叶变换建立了时间函数和频谱函数之间转换关系。

在实际信号分析中，经常需要对信号的时域和频域之间的对应关系及转换规律有一个清楚而深入的理解。

因此有必要讨论傅里叶变换的基本性质，并说明其应用。

一、线性傅里叶变换是一种线性运算。

若则其中a和b均为常数，它的证明只需根据傅里叶变换的定义即可得出。

例3-6利用傅里叶变换的线性性质求单位阶跃信号的频谱函数。

解因由式(3-55)得二、对称性若则证明因为有将上式中变量换为x，积分结果不变，即再将t用代之，上述关系依然成立，即最后再将x用t代替，则得所以证毕若是一个偶函数，即，相应有，则式(3-56)成为可见，傅里叶变换之间存在着对称关系，即信号波形与信号频谱函数的波形有着互相置换的关系，其幅度之比为常数。

式中的表示频谱函数坐标轴必须正负对调。

例如：例3-7若信号的傅里叶变换为试求。

解将中的换成t，并考虑为的实函数，有该信号的傅里叶变换由式(3-54)可知为根据对称性故再将中的换成t，则得为抽样函数，其波形和频谱如图3-20所示。

三、折叠性若则四、尺度变换性若则证明因a＞0，由令，则，代入前式，可得函数表示沿时间轴压缩(或时间尺度扩展)a倍，而则表示沿频率轴扩展(或频率尺度压缩)a倍。

该性质反映了信号的持续时间与其占有频带成反比，信号持续时间压缩的倍数恰好等于占有频带的展宽倍数，反之亦然。

例3-8已知,求频谱函数。

解前面已讨论了的频谱函数，且根据尺度变换性，信号比的时间尺度扩展一倍，即波形压缩了一半，因此其频谱函数两种信号的波形及频谱函数如图3-21所示。

五、时移性若则此性质可根据傅里叶变换定义不难得到证明。

它表明若在时域平移时间，则其频谱函数的振幅并不改变，但其相位却将改变。

例3-9求的频谱函数。

解:根据前面所讨论的矩形脉冲信号和傅里叶变换的时移性，有六、频移性若则证明证毕频移性说明若信号乘以，相当于信号所分解的每一指数分量都乘以，这就使频谱中的每条谱线都必须平移，亦即整个频谱相应地搬移了位置。

傅里叶变换

傅里叶变换

1 2
F1
ω 2
e j3ω
F1ω Ff1t
Ff1 t F1ω
对t时移6, 得
Ff16 t F1ωe j6ω
对t压缩2倍
F f1 6
2t
1 2
F1
ω 2
e j 3ω
方法三 利用傅里叶变换的性质
Ff at t0
1 a
F
ω
e
t j
0
a
a
上上 a -2, t0 6上上上上上上
F f1 6
方法二：利用傅里叶变换的积分性质
f t 1 f1(t)
f1(t)为f2 (t)的积分
O
1
1 2
t
f
A
t
1
O1
t
f t
2 1
F2
ω
Sa
ω 2
e
jω
上上
F1 ω
πω
1
jω
Sa
ω 2
ejω
Sa ω ejω
πω 2
jω
Sa ω ejω
F ω F1 F1ω 3 π δω
2 jω
O1
t
jbn )
Fn
F n
1 2
cn
1 2
dn
1 2
an2 bn2
Fn Fn cn
Fn Fn an
bn j(Fn Fn )
Fn 是 n1 的偶函数。
(3)函数的时域对称性与傅里叶系数的关系 ①实偶函数的傅里叶级数中不包含正弦项，只可能包含直流项和余弦项。 ②实奇数的傅里叶级数中不包含余弦项和直流项，只可能包含正弦项。 ③实奇谐函数的傅里叶级数中只可能包含基波和几次谐波的正弦、余弦项，而不包含偶次 谐波项。 2.傅里叶变换 傅里叶变换定义为

信号处理过程中的几种常见傅里叶相关的变换

信号处理过程中的几种常见傅里叶相关的变换

信号处理过程中的⼏种常见傅⾥叶相关的变换学习了信号与系统及数字信号处理之后，什么感觉呢？这尼玛讲的什么玩意啊？数字数字信号处理考了62分哦。

这两天，⼜看了看，因为可能要⽤到的唉。

好像是这么回事：我的理解吧，是这样的，对于各种变换⽆⾮就是通过数学公式把⼀个函数从⼀个域变到另⼀个域。

变来变去发现它有点物理意义了呢，也或着奔着它的物理意义去的。

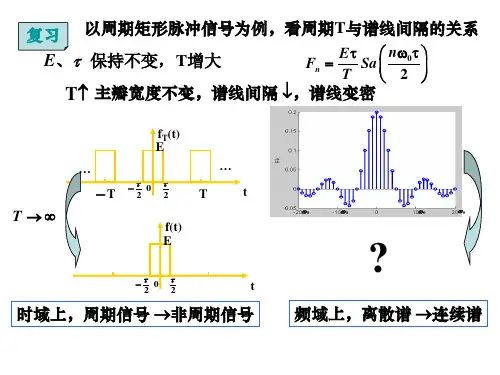
对于模拟信号：1. 分解为傅⾥叶级数的情况：信号是⼜时间 t 变化，并且为周期性的哦，这时，就可以把这个信号分解为⼀系列的正弦或余弦相叠加⽽成。

（此时的频域上为离散的哦，因为这⼀系列正弦波的頻率为基頻的整数倍）。

（可以看出：时域为周期的，频域⽽为离散的）说明了：对于时间上为周期的，它的频域为离散的。

还想说明⼀点，当我们⽤指数形式表⽰傅⾥叶级数时，它的系数F n与 F-n ⼀定是共轭的哦，如果不是共轭，它就展不成三⾓函数的形式了，（对于这点，由于看了⼀本书上的⼀个例⼦的写错了，我纠结了不⼩⼀会，后来可以通过举例⼦得到）变换公式：要知道，复幅度 Fn 的模即为幅度谱、⽽ Fn 的辐⾓主值（-pi， pi）即为相位谱啊；⽽后⾯的 e jnwt 这个不⽤管，它的作⽤是与 Fn 相乘以后得到 f(t)的；欧拉也太⽜逼了吧，这么抽象的三⾓函数的欧拉公式他是怎么搞出来的2. 分解为傅⾥叶变换的形式：对于⾮周期信号，则分解为傅⾥叶变换的样⼦啦。

因为吧，这时相当于周期为⽆穷⼤的周期信号，然后呢，它的基频相当于⽆穷⼩，所以就⽤连续的频域来进⾏变换，所以就有了傅⾥叶变换啦。

它就相当于把信号分解为了分布在全部頻域上的⼀系列正弦信号相叠加。

对于周期信号，如果你⾮要进⾏傅⾥中变换，也可以，但是要引⽤冲激函数，那么它的傅⾥叶变换由以前的⼀个个的散值变为了⼀个个离散的冲激函数。

（看看下图就知道什么意思啦）对于周期函数的⼀个周期内作傅⾥叶变换会怎么样呢？？因为它不是周期的嘛，它的图像想想的话⼀定是连续的，因为它不是周期的嘛，它的样⼦就是（如果按如图上⾯的例⼦来的话）上图中的包络。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(1)在任意周期内存在有限个第一类间断点； (2)在任意周期内存在有限个的极值点； (3)在任意周期上是绝对可积的，即
t0T f(t)dt
t0
a
3
可以展开为三角形20 ts b 1si0 n t b 2si2n 0 t
a 0 (a nco n0 ts b nsinn 0 t)
n 1
式中,
1
a0 T
T
2 -T
2
f (t) dt
an
2 T
T
2 T
2
f(t)cons0td
t
bn
2 T
T
2 T
2
f(t)sinn0td
t
式中，ω0=2π/T
a
4
利用三角函数的边角关系， 还可以将一般
三角形式化为标准的三角形式
c0 a0
n1
cn an2 bn2
a
a0
1 T
T
2 -T
f (t) dt
2
an
2 T
T
2 T
2
f(t)cons0td
t
bn
2 T
T
2 T
f(t)sinn0tdt
2
2
周期信号的傅里叶变换——傅里叶级数
1、 三角函数式傅里叶级数
若周期函数 f (t) 满足狄里赫利（ Dirichlet）条件:
2、指数形式的傅里叶级数
f (t) Fnejn0t n
式中，
F nT 1 T 2 T 2f(t)ej n 0td t
证明
- n
傅里叶复系数
Ne xt
a
11
Fn还可以表示成模和幅角的形式
式中，
Fn Fnejn Fn ejn
a b Fn
1 2
2 2
n
n
n
arctan
bn an
n
Fn 12（an - jbn）
cn 2
1
11
2
π n
4
0
0
0
0
－π4
0 0 0 0
－π
2
(a) 振幅频谱图
(b) 相位频谱图
例1的频谱图
a
9
周期信号的傅里叶变换——傅里叶级数
2、指数形式的傅里叶级数
f (t) Fnejn0t n
式中，
F nT 1 T 2 T 2f(t)ej n 0td t
证明
- n
傅里叶复系数
a
10
周期信号的傅里叶变换——傅里叶级数
f(t)12co0 st (4)co2 s0t(54 )1 2co3 s0t(2) 12co0 st (4)co2 s0t(4)1 2co3 s0t(2)
振幅谱与相位谱如下图所示。
1
f( t) 1 2 co 0 t 4 s ) c ( 2 o 0 t s 4 ) (2 c3 o 0 t s 2 )(
式中，
c0
a0
1 T
T
2 -T
2
f (t)dt
cn an2bn2,narctaban nn
a
6
周期信号的傅里叶变换——傅里叶级数
1、 三角函数式傅里叶级数
任何满足狄里赫利条件的周期为T的函数f(t),
可以展开成如下两种形式的三角级数：
f(t)a0 (anco0tsbnsin 0t)正、余弦级数形式 n 1
F0 Fnej n0t
*
Fnej
n0t
n1
n1
*
F0 a0 是实数 Fn与 ， Fn是一对共轭复数
Fn1 2（ an-jn b ）F *， n1 2（ anjn b ）
a
18
F n1 2 （ an-jn b ）F *， n1 2 （ anjn b ）
由三角形式的傅里叶系数定义式
an
2 T
傅里叶（Fourier）变换
周期信号的傅里叶变换——傅里叶级数 非周期信号的傅里叶变换 傅里叶变换性质
a
1
周期信号的傅里叶变换——傅里叶级数
1、 三角函数式傅里叶级数
或2f、(t)指a 数0 形n 式 1的(a 傅nc里o 叶0t级s 数b nsi n 0t)
f(t)c0 cncon s0t(n)
a
12
三角形式与指数形式系数之间的关系
f(t)a0 (anco 0tsbnsi n 0t)
或
n 1
f(t)c0 cncon s0t(n)
n1
f (t) Fnejn0t n
Fn
1 T
T
2 T
2
f(t)ejn0tdt
F0
a0
c0
1 T
T
2 -T
2
f(t)dt
F nF nejn1 2a njn b1 2cnejn
三角函数 形式的频 谱图
cn 2
1
11
2
0 0 0 0
(a) 振幅频谱
a
π n
4
0
0
0
0
－π4
－π2
(b) 相位频谱
Next
14
a
15
傅里叶级数指数形式 推导
a
16
利用欧拉公式 ej n0co n0 sjsinn0
cos
n0
1 2
(e
jn 0
e jn 0
)
sin n0
1 2j
(e jn0
T
2 T
2
f(t)cons0tdt
bn
2 T
T
2 T
2
f(t)sinn0td
t
可知：
an是 n 0 的偶函数，bn是 n 0 的奇函数
当n换为-n时，有a-n= an, b-n=- bn，从而
12（a-n-jb-n） 12（anjbn）
e jn 0 )
可以将正、余弦形式的傅里叶级数进一步写成
a
17
f(t)a0 (anco 0tsbnsi n 0t)
f (t) Fnejn0t n
a a 00 n n n 1 1 1 ((a a n n-2 ejj n n b 0te 2 je n 0tj n0ta n b 2 njen jb e n0 t2 j n je 0t )j n0t)
a b Fn 1 2
2
n
n 21 2cn
1 例 的指数形式频谱图如下图所示。
1 12 4
Fn
c1
1
2 c2
2 c3
2
π
n
2
π
π
4
4
－0
0
0
－0 －0 0
0
－0 －0 －0 0 0 0 0
－π4
－π4
－π2
双边频(谱a) （幅度D频o谱uble Side Band)
(b) 相位频谱
单边频谱（Single Side Band)
f (t) a0 (an cos0t bn sin0t)
n1
a0
n1
an2 bn2
an an2 bn2
cos0t
bn an2 bn2
sin0t
a0 cn(cosn cosn0t sinn sinn0t)
n1
c0 cn cos(n0t n)
n1
a
5
f(t) c0 cncon s0t(n) n1
或
f(t) c0 cncon s0t(n) n1
谐波形式
ω0是基谐波角频率,简称基波频率。
a
7
1 例 已知周期信号f(t)如下， 画出其频谱图。
5
1
f( t) 1 2 c0 o t c s2 o 0 t s 4 ) (2 si 0 t n 2 s3 i0 tn
解 ： 将f(t)整理为标准形式