拉氏变换表(包含计算公式)

附录A拉普拉斯变换及反变换3． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

设)(s F 是s 的有理真分式1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- （m n >）式中系数n n a a a a ,,...,,110-，m m b b b b ,,,110- 都是实常数；n m ,是正整数。

按代数定理可将)(s F 展开为部分分式。

分以下两种情况讨论。

① 0)(=s A 无重根这时，F(s)可展开为n 个简单的部分分式之和的形式。

∑=-=-++-++-+-=ni ii n n i i s s c s s c s s c s s c s s c s F 12211)( （F-1）式中，n s s s ,,,21 是特征方程A(s)＝0的根。

i c 为待定常数，称为F(s)在i s 处的留数，可按下式计算：)()(l i m s F s s c i s s i i-=→ （F-2）或iss i s A s B c ='=)()( （F-3）式中，)(s A '为)(s A 对s 的一阶导数。

根据拉氏变换的性质，从式（F-1）可求得原函数[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 111)()(＝ts ni i i ec -=∑1(F-4)②0)(=s A 有重根设0)(=s A 有r 重根1s ，F(s)可写为())()()()(11n r rs s s s s s s B s F ---=+ =nn i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++-- 11111111)()()(式中，1s 为F(s)的r 重根，1+r s ，…, n s 为F(s)的n-r 个单根；其中，1+r c ，…, n c 仍按式(F-2)或(F-3)计算，r c ，1-r c ，…, 1c 则按下式计算：)()(lim 11s F s s c r s s r -=→)]()([lim111s F s s dsdc r s s r -=→- )()(lim !11)()(1s F s s dsd j c r j j s s jr -=→- (F-5))()(lim )!1(11)1()1(11s F s s dsd r c r r r s s --=--→原函数)(t f 为[])()(1s F L t f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L 111111111)()()( t s nr i i t s r r r r ie c e c t c t r c t r c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=1122111)!2()!1( （F-6）。

常用的拉氏变换表在工程技术和科学研究中，拉氏变换是一种非常重要的数学工具。

它能够将时域中的函数转换为复频域中的函数，从而使得许多问题的分析和求解变得更加简便。

而要熟练运用拉氏变换，掌握常用的拉氏变换表是必不可少的。

拉氏变换的定义为：对于一个定义在0, ＋∞）上的实值函数 f(t)，其拉氏变换 F(s)定义为：＼F(s) ＝＼int_{0}＾｛＼infty} f(t) e^｛st} dt\其中，s ＝σ ＋jω 是一个复变量。

下面我们来介绍一些常用的函数的拉氏变换：1、单位阶跃函数 u(t)单位阶跃函数在 t ＜ 0 时，函数值为 0；在t ≥ 0 时，函数值为 1。

其拉氏变换为：＼Lu(t) ＝＼frac{1}｛s}＼2、单位脉冲函数δ(t)单位脉冲函数在 t ＝ 0 时，函数值为无穷大，且在整个时间轴上的积分值为 1。

其拉氏变换为：＼Lδ(t) ＝ 1\3、指数函数 e^（at) （a 为常数）其拉氏变换为：＼Le^｛at} ＝＼frac{1}｛s ＋ a}＼4、正弦函数sin(ωt)其拉氏变换为：＼Lsin(ωt) ＝＼frac{＼omega}｛s^2 ＋＼omega^2}＼5、余弦函数cos(ωt)其拉氏变换为：＼Lcos(ωt) ＝＼frac{s}｛s^2 ＋＼omega^2}＼6、 t 的幂函数 t^n （n 为正整数）其拉氏变换为：＼Lt^n ＝＼frac{n!｝｛s^｛n ＋ 1}｝＼7、斜坡函数 t其拉氏变换为：＼Lt ＝＼frac{1}｛s^2}＼8、二次斜坡函数 t^2其拉氏变换为：＼Lt^2 ＝＼frac{2!｝｛s^3} ＝＼frac{2}｛s^3}＼掌握这些常用函数的拉氏变换，可以帮助我们在解决各种问题时快速进行变换和求解。

例如，在电路分析中，通过拉氏变换可以将时域中的电路方程转换为复频域中的方程，从而更方便地求解电路的响应。

在控制系统中，拉氏变换也有着广泛的应用。

通过对系统的输入和输出进行拉氏变换，可以得到系统的传递函数，从而对系统的性能进行分析和设计。

代入初始条件，得：
X ( s) = 1 s +8 s−2 (s + 2 ) X ( s ) + 2Y ( s ) = s − 2 解得： Y ( s ) = 3 − 2 X ( s ) + ( s + 1)Y ( s ) = 3s + 1 s−2 s−2 作反变换，得：x(t ) = e 2t , y (t ) = 3 ⋅ e 2t
其中 k i = F ( s ) ⋅ ( s − pi ) | s = p i ，则：f (t ) = k1 e p1t + k 2 e p 2t + .... + k n e p nt 2，当解出s等于一对共轭复根，即 s = p1,2 = σ ± jw ，则： 1 1 1 F (s) = = = ( s − p1)( s − p 2) s 2 − ( p1 + p 2) s + p1 p 2 s 2 − 2σs + (σ 2 + w2)
拉氏变换公式表
f (t ) = −u (t ) + t + e−t = −1 + t + e−t , (t ≥ 0 )
若F(s)不是有理真分式，则化为 多项式与真分式之和。
例2：已知 F (s ) =
as + b c 解：令F (s ) = 2 + (s + 2s + 3) s + 2
(s2 + 2s + 3)(s + 2) ，求其反变换。
1 f (t )满足divichlet条件。 ） 2）若f (t )是指数阶函数，则必须存在M > 0，使当t > t 0 时， (t ) ≤ M ⋅ ect f

t 0
s
lim f (t) lim sF (s)
t
s0
L
d dt
f
(t)
SF(s)
f
(0)
L
d
2f dt
(t
2
)
S 2F(s)
Sf (0)
f
(0)
f (0 ) lim f (t) lim sF (s)
t 0
s
lim f (t) lim sF (s)
t
s0
Lf (t)g(t)= F sGs
18
1
t n 1-2
e -nt sinn 1-2
1 e -nt sin(n 1-2 t-
) 1-2
19
=
arctan
1-2
1
s2+2ns+n2
s
s2+2ns+n2
典型时间函数的拉普拉斯变换
序号
原函数 f(t) (t >0)
1- 1 e -nt sin(n 1-2 t +
) 1-2
20
1-2
= arctan
典型常见函数 拉氏变换表
典型常见函数拉氏变换表
序号 1
原函数 f(t) (t >0)
1 (单位阶跃函数)
象函数 F(s)=L[f(t)]
1 s
2
(t) (单位脉冲函数)
1
3
K (常数)
K s
4
t (单位斜坡函数)
1 s2
典型常见时间函数拉氏变换表
序号 5 6 7 8
原函数 f(t) (t >0)
t n (n=1, 2, …) e -at

附录A 拉普拉斯变换及反变换4194204213． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

设)(s F 是s 的有理真分式1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==----ΛΛ （m n >） 式中系数n n a a a a ,,...,,110-，m m b b b b ,,,110-Λ都是实常数；n m ,是正整数。

按代数定理可将)(s F 展开为部分分式。

分以下两种情况讨论。

① 0)(=s A 无重根这时，F(s)可展开为n 个简单的部分分式之和的形式。

∑=-=-++-++-+-=ni ii n n i i s s c s s c s s c s s c s s c s F 12211)(ΛΛ （F-1）式中，n s s s ,,,21Λ是特征方程A(s)＝0的根。

i c 为待定常数，称为F(s)在i s 处的留数，可按下式计算：)()(lim s F s s c i s s i i-=→ （F-2）或iss i s A s B c ='=)()( （F-3）式中，)(s A '为)(s A 对s 的一阶导数。

根据拉氏变换的性质，从式（F-1）可求得原函数[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 111)()(＝ts n i i ie c -=∑1(F-4)②0)(=s A 有重根设0)(=s A 有r 重根1s ，F(s)可写为())()()()(11n r rs s s s s s s B s F ---=+Λ =nn i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++--ΛΛΛ11111111)()()( 式中，1s 为F(s)的r 重根，1+r s ，…, n s 为F(s)的n-r 个单根；422其中，1+r c ，…, n c 仍按式(F-2)或(F-3)计算，r c ，1-r c ，…, 1c 则按下式计算：)()(lim 11s F s s c r s s r -=→)]()([lim111s F s s dsdc r s s r -=→- M)()(lim !11)()(1s F s s dsd j c r j j s s jr -=→- (F-5) M)()(lim )!1(11)1()1(11s F s s dsd r c r r r s s --=--→原函数)(t f 为 [])()(1s F Lt f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L ΛΛΛ111111111)()()( t s nr i i t s r r r r ie c e c t c t r c t r c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=1122111)!2()!1(Λ （F-6）。

式中， s1 为 F(s)的 r 重根， sr 1 ，…, s n 为 F(s)的 n-r 个单根； 其中， c r 1 ，…, cn 仍按式(F-2)或(F-3)计算， cr ， cr 1 ，…, c1 则按下式计算：
c r lim ( s s1 ) r F ( s )
s s1
c r 1 lim
z 2 ze aT cos T z 2 ze aT cos T e 2 aT
2
sa (s a) 2 2
1 s (1 / T ) ln a
z za
3． 用查表法进行拉氏反变换 用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行 反变换。设 F ( s ) 是 s 的有理真分式
1 s2
1 s3
t
t2 2
Tz ( z 1) 2
T 2 z ( z 1) 2( z 1)3
lim (1) n n z ( ) n a 0 n! a z e aT
z z e aT
1 s n 1
1 sa
tn n!
e at te
at
1 (s a) 2
a s(s a) ba ( s a )( s b)
F (s)
B ( s ) bm s m bm 1 s m 1 b1 s b0 A( s ) a n s n a n 1 s n 1 中系数 a 0 , a1 ,..., a n 1 , a n ， b0 , b1 , bm 1 , bm 都是实常数； m , n 是正整数。按代数定理可 将 F ( s ) 展开为部分分式。分以下两种情况讨论。 ①
表a2常用函数的拉氏变换和z变换表拉氏变换es时间函数et42112用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开然后逐项查表进行反变换

（完整）Laplace拉氏变换公式表编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（完整）Laplace拉氏变换公式表）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（完整）Laplace拉氏变换公式表的全部内容。

附录A 拉普拉斯变换及反变换1。

表A—1 拉氏变换的基本性质2．表A-2 常用函数的拉氏变换和z变换表3． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

设)(s F 是s 的有理真分式1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- （m n >） 式中系数n n a a a a ,,...,,110-，m m b b b b ,,,110- 都是实常数；n m ,是正整数。

按代数定理可将)(s F 展开为部分分式。

分以下两种情况讨论。

① 0)(=s A 无重根这时,F （s ）可展开为n 个简单的部分分式之和的形式。

∑=-=-++-++-+-=ni ii n n i i s s c s s c s s c s s c s s c s F 12211)( （F-1）式中，n s s s ,,,21 是特征方程A （s ）＝0的根。

i c 为待定常数,称为F （s ）在i s 处的留数,可按下式计算：)()(lim s F s s c i s s i i-=→ （F-2) 或iss i s A s B c ='=)()( (F-3）式中，)(s A '为)(s A 对s 的一阶导数。

拉氏变换定义计算公式及常用拉氏变换反变换拉氏变换定义计算公式及常用拉氏变换反变换拉氏变换定义.计算.公式及常用拉氏变换反变换****拉普拉斯转换及反华转换****定义：如果定义：就是一个关于的函数，使当就是一个为丛藓科扭口藓变量；是一个运算符号，它代表对其对象进行拉普拉斯积分的拉普拉斯变换结果。

则的拉普拉斯转换由以下式子得出：2．表a-2常用函数的拉氏变换和z变换表3．用换算法展开拉氏反华转换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

设f(s)是s的有理真分式b(s)bmsm bm1sm1b1s b0f(s)（n m）a(s)ansn an1sn1a1s a0式中系数a0,a1,...,an1,an，b0,b1,bm1,bm都是实常数；m,n是正整数。

按代数定理可将f(s)展开为部分分式。

分以下两种情况讨论。

①a(s)0无重根这时，f(s)可以进行为n个直观的部分分式之和的形式。

cicncc1c2f(s)i（f-1）s s1s s2s sis sni1s si式中，s1,s2,,sn就是特征方程a(s)＝0的木。

ci为未定常数，称作f(s)在si处的留数，可以按下式排序：或ci lim(s si)f(s)（f-2）a(s)s s式中，a(s)为a(s)对s的一阶导数。

根据拉氏变换的性质，从式（f-1）可求得原函数n nci stf(t)l f(s)l＝(f-4)ce ii1s si i1a(s)0有重根设a(s)0存有r重根s1，f(s)展毛为(s s1)(s sr1)(s sn)cicncrcr1c1cr1rr1(s s1)(s s1)(s s1)s sr1s sis sn式中，s1为f(s)的r重根，sr1，…,sn为f(s)的n-r个单根；其中，cr1，…,cn仍按式(f-2)或(f-3)排序，cr，cr1，…,c1则按下式排序：cr lim(s s1)rf(s)cr1lim[(s s1)rf(s)]dslim(j)(s s1)rf(s)(f-5)j!s s1ds1d(r1)c1lim(r1)(s s1)rf(s)(r1)!s s1ds原函数f(t)为f(t)lcrcicn cr1c1cr1l1rr1(s s1)s sr1s sis sn(s s1)(s s1)crtr1cr1tr2c s1(r1)!r2)!2t c1 e i ciest(r1。

Laplace拉氏变换公式表1. 常数变换：对于常数C，其拉普拉斯变换为C/s，其中s是复数频率。

2. 幂函数变换：对于幂函数t^n，其中n为实数，其拉普拉斯变换为n!/s^(n+1)。

3. 指数函数变换：对于指数函数e^(at)，其中a为实数，其拉普拉斯变换为1/(sa)。

4. 正弦函数变换：对于正弦函数sin(at)，其中a为实数，其拉普拉斯变换为a/(s^2+a^2)。

5. 余弦函数变换：对于余弦函数cos(at)，其中a为实数，其拉普拉斯变换为s/(s^2+a^2)。

6. 双曲正弦函数变换：对于双曲正弦函数sinh(at)，其中a为实数，其拉普拉斯变换为a/(s^2a^2)。

7. 双曲余弦函数变换：对于双曲余弦函数cosh(at)，其中a为实数，其拉普拉斯变换为s/(s^2a^2)。

8. 指数衰减正弦函数变换：对于指数衰减正弦函数e^(at)sin(bt)，其中a和b为实数，其拉普拉斯变换为b/(s+a)^2+b^2。

9. 指数衰减余弦函数变换：对于指数衰减余弦函数e^(at)cos(bt)，其中a和b为实数，其拉普拉斯变换为s+a)/(s+a)^2+b^2。

10. 指数增长正弦函数变换：对于指数增长正弦函数e^(at)sin(bt)，其中a和b为实数，其拉普拉斯变换为b/(sa)^2+b^2。

Laplace拉氏变换公式表11. 幂函数与指数函数的乘积变换：对于函数t^n e^(at)，其中n为实数，a为实数，其拉普拉斯变换为n!/(sa)^(n+1)。

12. 幂函数与正弦函数的乘积变换：对于函数t^n sin(at)，其中n为实数，a为实数，其拉普拉斯变换可以通过分部积分法得到。

13. 幂函数与余弦函数的乘积变换：对于函数t^n cos(at)，其中n为实数，a为实数，其拉普拉斯变换可以通过分部积分法得到。

14. 指数函数与正弦函数的乘积变换：对于函数e^(at) sin(bt)，其中a和b为实数，其拉普拉斯变换为b/(sa)^2+b^2。

****拉普拉斯变换及反变换****定义：如果定义：• 是一个关于的函数，使得当时候，；•是一个复变量；• 是一个运算符号，它代表对其对象进行拉普拉斯积分；是的拉普拉斯变换结果。

则的拉普拉斯变换由下列式子给出：1线性定理齐次性)()]([s aF t af L =叠加性)()()]()([2121s F s F t f t f L ±=±2微分定理一般形式=-=][- -=-=----=-∑11)1()1(1222)()()0()()(0)0(')(])([)0()(])([k k k k nk k n nnn dt t f d t f f s s F s dt t f d L f sf s F s dt t f d L f s sF dt t df L ）（ 初始条件为0时)(])([s F s dtt f d L n nn =2．表A-2 常用函数的拉氏变换和z变换表3． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

设)(s F 是s 的有理真分式1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- （m n >） 式中系数n n a a a a ,,...,,110-，m m b b b b ,,,110- 都是实常数；n m ,是正整数。

按代数定理可将)(s F 展开为部分分式。

分以下两种情况讨论。

① 0)(=s A 无重根这时，F(s)可展开为n 个简单的部分分式之和的形式。

∑=-=-++-++-+-=ni ii n n i i s s c s s c s s c s s c s s c s F 12211)( （F-1）式中，n s s s ,,,21 是特征方程A(s)＝0的根。

n
F ( s)
L[ f (t )dt ]
一般形式 3 积分定理
L[ f (t )(dt ) 2 ]
共n个
2 F ( s ) [ f (t )dt ]t 0 [ f (t )(dt ) ]t 0 s2 s2 s
共n个 F ( s) n 1 n L[ f (t )(dt ) ] n n k 1 [ f (t )(dt ) n ]t 0 s k 1 s
B( s ) b s b s b s b F (s ) A(s ) a s a s a s a
m m 1 m m 1 1 n n 1 n n 1 1 0
0
（n m）
式中系数 a
0
, a ,..., a , a ， b , b ,b , b 都是实常数； m, n 是正整数。按
1(t )
z z 1
1 s2
1 s3
t
t2 2
Tz ( z 1) 2
T 2 z ( z 1) 2( z 1) 3
1 s n 1
1 sa
tn n!
lim
( 1) n n z ( ) n a 0 n! a z e aT
z z e aT
e at te
at
拉普拉斯变换及其反变换表表a1拉氏变换的基本性质1线性定理齐次性叠加性2微分定理一般形式初始条件为0时3积分定理一般形式初始条件为0时4延迟定理或称域平移定理5衰减定理或称域平移定理6终值定理7初值定理8卷积定理2
拉普拉斯变换及其反变换表
1.表 A-1 拉氏变换的基本性质
1 线性定理 齐次性 叠加性
c c t t c t c e c e (r 2)! (r 1)!

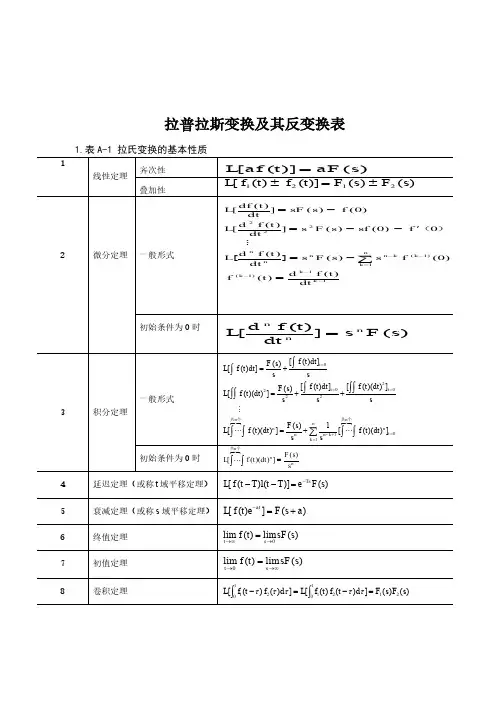
1拉氏变换及反变换公式1. 拉氏变换的基本性质 1线性定理齐次性)()]([s aF t af L =叠加性)()()]()([2121s F s F t f t f L ±=±2微分定理一般形式=-=][ '- -=-=----=-∑11)1()1(1222)()()0()()(0)0()(])([)0()(])([k k k k nk k n n nn dt t f d t f f s s F s dt t f d L f sf s F s dt t f d L f s sF dt t df L ）（ 初始条件为0时)(])([s F s dtt f d L n nn = 3积分定理一般形式∑⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰==+-===+=++=+=nk t n n k n n nn t t t dt t f s s s F dt t f L sdt t f s dt t f s s F dt t f L sdt t f s s F dt t f L 101022022]))(([1)(])()([]))(([])([)(]))(([])([)(])([个共个共初始条件为0时n n n ss F dt t f L )(]))(([=⎰⎰个共4 延迟定理（或称t 域平移定理） )()](1)([s F e T t T t f L Ts -=--5 衰减定理（或称s 域平移定理） )(])([a s F e t f L at +=-6 终值定理 )(lim )(lim 0s sF t f s t →∞→=7 初值定理 )(lim )(lim 0s sF t f s t ∞→→=8 卷积定理)()(])()([])()([21021021s F s F d t f t f L d f t f L tt =-=-⎰⎰τττττ22． 常用函数的拉氏变换和z 变换表 序号 拉氏变换E(s)时间函数e(t) Z 变换E(z)1 1δ(t) 12 Tse --11∑∞=-=0)()(n T nT t t δδ1-z z 3 s1 )(1t1-z z 4 21s t2)1(-z Tz5 31s 22t32)1(2)1(-+z z z T6 11+n s!n t n)(!)1(lim 0aT n n n a ez z a n -→-∂∂- 7 as +1 at e - aTe z z-- 8 2)(1a s +atte- 2)(aT aT e z Tze ---9 )(a s s a+ ate--1))(1()1(aT aT e z z z e ----- 10 ))((b s a s ab ++-bt at e e --- bTaT e z ze z z ----- 11 22ωω+s t ωsin1cos 2sin 2+-T z z Tz ωω 12 22ω+s st ωcos1cos 2)cos (2+--T z z T z z ωω13 22)(ωω++a s t e atωsin - aTaT aT eT ze z Tze 22cos 2sin ---+-ωω 14 22)(ω+++a s a st eatωcos -aTaT aT e T ze z T ze z 222cos 2cos ---+--ωω15aT s ln )/1(1- T t a /az z -33． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

拉普拉斯变换及反变换1. 表 A-1 拉氏变换的基本性质1齐次性线性定理叠加性2微分定一般形式理L[af ( t)] aF (s)L[ f1 (t ) f 2 ( t )] F1 ( s) F2 ( s) L[ df (t ) ] sF (s) f (0)dtL[d 2 f (t) 2f（）dt 2 ] s F (s) sf (0) 0n nd f (t ) n n k ( k 1 )L dt n s F (s) k 1 s f (0) f ( k 1) (t ) d k 1 f (t )dt k 1初始条件为 0 时一般形式3积分定理初始条件为 0 时4延迟定理（或称 t 域平移定理）5衰减定理（或称 s 域平移定理）6终值定理7初值定理8卷积定理L[d n f (t) ndt n ] s F (s)L[ f (t)dt]F (s) [ f (t)dt] t 0s sL[ f (t)(dt)2 ] F (s)[ f (t )dt]t 0[ f (t)( dt) 2 ] t 0s2 ss2共 n个n共 n个nF (s) 1 nL[ f (t )(dt) ] 1 [ f (t)( dt) ] t 0nk 1 sn ks共 n个F (s)L[ f (t )( dt) n ]s nL[ f (t T )] e Ts F ( s)L[ f ( t)e at ] F (s a)lim f (t ) lim sF (s)t s0lim f (t ) lim sF ( s)t 0 st 1 ( ) 2 ( ) ] [ t 1 ( ) 2 ( ) ] 1() 2()[ f d L f f t dL f t t F s F s0 012．表 A-2 常用函数的拉氏变换和z 变换表拉氏变换E(s)111 e Ts1s12s13s1s n 11s a1( s a) 2as( s a)b a( s a)(s b)s2 2ss2 2( s a) 2 2s a( s a)2 21s (1 / T ) ln a 时间函数 e(t)δ(t)T (t )(t nT )n01(t )tt 22ntn!e atte at1 e ate at e btsin tcos te at sin te at cos ta t / T23．用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

2． 常用函数的拉氏变换和 z 变换表
序 号 拉氏变换 E(s)
时间函数 e(t)
1
1
δ(t)
2
1
1 nT) n0
1(t )
4
1
t
s2
5
1
t2
s3
2
6
1
tn
s n1
n!
7
1
sa
eat
8
1 (s a)2
te at
9
a
s(s a)
s si
式中， A(s) 为 A(s) 对 s 的一阶导数。根据拉氏变换的性质，从式（F-1）可求得原函数
f (t) L1
F(s)

L1

n
i1
s
ci si

＝
n i 1
ci e sit
② A(s) 0 有重根
设 A(s) 0 有 r 重根 s1 ，F(s)可写为
z za
2
3． 用查表法进行拉氏反变换
用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。
设 F (s) 是 s 的有理真分式
F (s)

B(s) A(s)

bm s m an s n
bm1s m1 b1s b0 an1s n1 a1s a0
Fs
B(s)
(s s1 )r (s sr1 )(s sn )
=
(s
cr s1
)
r

cr 1 (s s1 )r1

c1 (s s1)

cr 1 s sr1

附录A 拉普拉斯变换及反变换表A-1 拉氏变换的基本性质齐次性)()]([s aF t af L =1线性定理叠加性)()()]()([2121s F s F t f t f L ±=±一般形式=-=][ '- -=-=----=-∑11)1()1(1222)()()0()()(0)0()(])([)0()(])([k k k k nk k n n nn dt t f d t f f s s F s dt t f d L f sf s F s dt t f d L f s sF dt t df L）（2微分定理初始条件为0时)(])([s F s dtt f d L n nn =一般形式∑⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰==+-===+=++=+=n k t n n k n n nn t t t dt t f s s s F dt t f L sdt t f s dt t f s s F dt t f L sdt t f s s F dt t f L 101022022]))(([1)(])()([]))(([])([)(]))(([])([)(])([个共个共3积分定理初始条件为0时nn n ss F dt t f L )(]))(([=⎰⎰个共 4延迟定理（或称域平移定理）t )()](1)([s F e T t T t f L Ts -=--5衰减定理（或称域平移定理）s )(])([a s F e t f L at +=-6终值定理)(lim )(lim 0s sF t f s t →∞→=7初值定理)(lim )(lim 0s sF t f s t ∞→→=8卷积定理)()(])()([])()([21021021s F s F d t f t f L d f t f L tt=-=-⎰⎰τττττ表A-2 常用函数的拉氏变换和z 变换表序号拉氏变换E(s)时间函数e(t)Z 变换E(z)11δ(t)12Tse --11∑∞=-=0)()(n T nT t t δδ1-z z 3s1)(1t 1-z z 421s t2)1(-z Tz 531s 22t 32)1(2)1(-+z z z T611+n s !n t n )(!)1(lim 0aTn n n a e z z a n -→-∂∂-7as +1ate-aTe z z--82)(1a s +atte -2)(aT aT e z Tze ---9)(a s s a +ate --1))(1()1(aT aT e z z z e -----10))((b s a s a b ++-btatee ---bT aT e z ze z z -----1122ωω+s tωsin 1cos 2sin 2+-T z z Tz ωω1222ω+s s tωcos 1cos 2)cos (2+--T z z T z z ωω1322)(ωω++a s t e at ωsin -aTaT aT e T ze z Tze 22cos 2sin ---+-ωω1422)(ω+++a s a s teatωcos -aTaT aT e T ze z T ze z 222cos 2cos ---+--ωω15aT s ln )/1(1-Tt a /az z -用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

附录A拉普拉斯变换及反变换1.表A-1拉氏变换的基本性质1线性定理齐次性£[形⑷2微分定理般形式]=vF ( f ]-ifJiOV f(硏-訂- r初始条件为时3积分定理般形式始条件为叠加性4延迟定理（或称•'域' 平移定理）5衰减定理（或称"域平移定理）6终值定理7初值定理8卷积定理2.表A-2常用函数的拉氏变换和z变换表，号拉氏变换E（s时间函数e（t Z变换E（z 1 1s (t11 2«.『一疗）1 一r t■fa •lim 00 = lim sF( s)3 inn1 J st7> IF] FJ 葺1 illIr?.- c? *T_ AT□rteU-■U!~ ■1 - L-(£- 1K *f- v',J )b- az z (& + *r)(b)-aT_ -f»r z- ez- lfffizsin 皿 TJ . 1 J ； 4 fJ!>lll tulz 2 - 2zcos w T + 1同COE 期门• ■-M.XI- 2 jctis *} f + Izc '1 Sin™ r1 —z ! - Ize " CDS (t )T v e456789101112133. 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项 查表进行反变换。

设是1的有理真分式()式中系数， 都是实常数； 是正整数。

按代数定理可将 展开为部分分式。

分 以下两种情况讨论。

①无重根 这时，F(s 可展开为n 个简单的部分分式之和的形式。

c CCC * I?尸($)=―+— + …+—+ …十一=22—i —-'一(F -1 )式中，―…*是特征方程A(s 二0的根。

为待定常数，称为F(s 在 处的留数，可按下式计算：c = lirn (耳一s)'(F-2)或(F-3)14C COS tyij? -ti )T + r15y- (1/ Tj-ln V式中，为|对、的一阶导数。