泰勒公式(泰勒中值定理)

泰勒公式展开泰勒公式也称为泰勒中值定理，是高等数学中的一个重要定理，也是考研数学中的一个重要考点，常用于函数极限的计算、中值问题和不等式的证明以及函数的无穷级数展开式中，因此大家应该理解并熟练掌握其应用。

f(x)=f(x0)+f′(x0)1!⋅(x−x0)+f′′(x0)2!⋅(x−x0)2+...+f(n)(x0)n!⋅(x−x0)n+Rn(x)f(x)=f(x0)+f′(x0)1!⋅(x−x0)+f″(x0)2!⋅(x−x0)2+...+f(n)(x0)n!⋅(x−x0)n+Rn(x) 即：f(x)=f(x0)+∑i=1nf(i)(x0)i!⋅(x−x0)i+Rn(x)即：f(x)=f(x0)+∑i=1nf(i)(x0)i!⋅(x−x0)i+Rn(x)其中Rn(x)Rn(x)表示泰勒公式的余项，可以估算近似的误差，相当于无穷小将其中的x0x0带入00就可以得到麦克劳林展开，即f(x)=f(0)+f′(0)1!⋅x+f′′(0)2!⋅x2+...+fn(0)n!⋅xnf(x)=f(0)+f′(0)1!⋅x+f″(0)2!⋅x2+...+fn(0)n!⋅xn 然后虽然我们知道了这两个公式,还是不会用诶(当然大佬可能都是知道怎么用的..然而我确是一脸懵233)..下面说两个实例展开y=sin(x)y=sin⁡(x)和y=cos(x)y=cos⁡(x)用y=sin(x)y=sin⁡(x)来说:前置知识:fn(x)=sin(x+nπ2)fn(x)=sin(x+nπ2)(推一下x=1、2、3...x=1、2、3...即可找到公式)然后我们需要求出f(0)f(0)的nn阶导,推一下发现f1(0)f3(0)f5(0)f7(0)=1=−1=1=−1f2(0)=0f4(0)=0f6(0)=0f8(0)=0f1(0)=1f2(0)=0f3(0)=−1f4(0)=0f5(0)=1f6(0)=0f7(0)=−1f8(0)=0也就是f2n−1(0)=(−1)n−1f2n−1(0)=(−1)n−1,f2n(0)=0f2n(0)=0 通过麦克劳林展开可以得到sin(x)=x1!−x33!+x55!−...+(−1)n−1x2n−1(2n−1)!sin(x)=x1!−x33!+x55!−...+(−1)n−1x2n−1(2n−1)!同理可以得到cos(x)=1−x22!+x44!−...+(−1)nx2n(2n)!cos(x)=1−x22!+x44!−...+(−1)nx2n(2n)!计算近似值前置知识:e=limx→0(1+x)1xe=limx→0(1+x)1x即e=limx→∞(1+1x)xe=limx→∞(1+1x)x因此令f(x)=exf(x)=ex通过麦克劳林展开可以得到ex=f(x)=e0+e01!⋅x+e02!⋅x2+...+e0n!⋅xn+Rn=1+x1!+x22!+x33!+...+xnn!+Rnex=f(x)=e0+e01!⋅x+e02!⋅x2+...+e0n!⋅xn+Rn=1+x1!+x22!+x33!+...+xnn!+Rn忽略余项得到ex≈1+x1!+x22!+x33!+...+xnn!+Rnex≈1+x1!+x22!+x33!+...+xnn! +Rn带入x=1x=1,e≈1+11!+12!+13!+...+1n!。

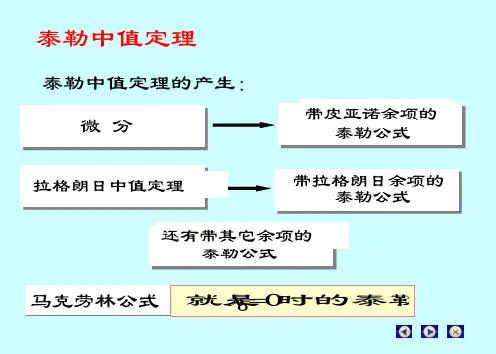
泰勒中值定理一、泰勒中值定理若)(x f 在含有0x 的某个区间I 内具有直到1n +阶导数，则当x I ∈时，有()20000000()()()()'()()()()()2!!n n n f x f x f x f x f x x x x x x x R x n ''=+-+-++-+ ，其中拉格朗日型余项(1)0()()(),(1)!n n n f R x x x n ξξ+=-+位于0x 与x 之间．当0n =时，泰勒中值定理就是拉格朗日中值定理．取00x =，()(1)2(0)(0)()()(0)'(0),2!!(1)!n n n nf f f f x f f x x x x x n n ξξθ+''=+++++=+ 位于0与x 之间，(0,1)θ∈，其为n 阶麦克劳林公式．二、基本函数的高阶导数公式⎪⎩⎪⎨⎧<=>=-mn x A m n n m n x n m n mn m !0)()( 1)()(!)1(1+±-=⎪⎭⎫ ⎝⎛±n n m a x n a x ， nn n a x n a x )()!1()1()][ln(1)(±--=±-，a a a nx n x ln )()(=， )2sin()(sin )(πn ax a ax n n +=，)2cos()(cos )(πn ax a ax n n +=；()()()()()()12120[()()]()(),[()()][()][()]nn n n n kn k k n k k u x k v x k u x k v x u x v x C u x v x -=+=+=⋅∑； 三、基本函数的麦克劳林展开式(1)2(1)(1)(1)(1)12!!mnm m m m m n x mx x x n ---++=+++++ ,1x < (2) ++-++-+-=++1)1(432)1ln(1432n x x x x x x n n )11(≤<-x (3) ++++++=!!3!2!1132n x x x x e n x)(+∞<<-∞x (4) +--+-+-=--)!12()1(!5!3sin 12153n x x x x x n n )(+∞<<-∞x (5) +-+-+-=)!2()1(!4!21cos 242n x x x x n n )(+∞<<-∞x 当0x →时，有233(1)(1)(2)(1)1()2!3!mm m m m m x mx x x o x ---+=++++12332111(1)1()2816x x x x o x +=+-++,233ln(1)()23x x x x o x +=-++2331()1!2!3!x x x x e o x =++++,23233ln ln ln 1()1!2!3!xa a a a x x x o x =++++355sin ()3!5!x x x x o x =-++,244cos 1()2!4!x x x o x =-++,3552tan ()315x x x x o x =+++3553arcsin ()640x x x x o x =+++,355arctan ()35x x x x o x =-++例1、求下列高阶导数)()(x yn（1）设502)54(+=x y ，则!100450)100(⋅=y ．（2）设232+-=x x x y ，求)(n y ． 解： ])2(2)1(1[!)1()21(2)11(11)()()(++-++⋅-=-++=n n n n n n x x n x x y． （3）设x y x y=-，则1(2,1)1!(1),2!()n n n n n n z n x z n y y x y ++∂∂=-=⋅∂-∂ （3）设x x y 44cos sin +=，则)24cos(4)4(cos 41)43()1()()()(πn x x y n n n n +=+=-．（4）设n n x x x y )4(cos )2(2π-+=，求)()(x f n ，)1()(n f ．解：()()()0()[(1)][(2)(cos )]4nn k n k nn n k n k x f x C x x π-==-+∑ 21)(2!3|)4(cos)2(!)1(n n x nnnnn n xx n C f=+==π．（5）设函数2()sin f x x x =，求 (2009)(0)f．解：321221sin [(1)]3!(21)!n n x x x x x x n --=-++-+- 52131(1)3!(21)!n n x x x n +-=-++-+- 则(2009)(0)12009!2007!f =，故(2009)(0)20082009f=⨯． 注（1）： 若01()nn f x a a x a x =++++ ，则()(0)()(0)(0)!n n f f x f f x x n '=++++ ，于是()(0)!n n f a n =，故()(0)!n n f n a =． 注（2）：若求(2009)()4fπ，则只能用莱布尼兹公式完成．例2、计算下列极限（1）4301sin sinlim tan x x x x x x →-+；（2）20(1)ln(1)lim 1x x x x x e →-++-；（3）21lim ln(1)x x x x →∞⎡⎤-+⎢⎥⎣⎦； （1）解：原式33303033000tan ~()sin 113!lim lim sin lim 6x x x x x x o x x x x x x x →→→+-=+==． （2）解：原式22222200(1)[()]()122lim lim 2x x x xx x x o x o x x x →→-+-+-+===-． （3）解：原式21222()ln(1)12lim lim 2x t x x t o x t t t t =∞-∞→∞→∞+-+=== 或（泰勒）2221111lim (())22x x x o x x x →∞⎡⎤=--+=⎢⎥⎣⎦．例3、设lim )0x ax b →+∞-=，求b a ,．解：10lim )lim x tx t bt aax b t =→+∞→--=3021001(2)()1()223lim lim 0333a t t t t o t bt o t t b b t t =→→++-⎡⎤==++-=-=⎢⎥⎣⎦∴ 32,1==b a ． 例4、当0→x 时，x x33tan -是关于x 的k 阶无穷小，则3=k ．解：（一）tan tan 00003331(tan )ln 3lim lim lim3limx x x x xk k kx x x x x x x x x -→→→→---== 3330()ln 33ln 3lim 3k k x x x o x x x =→++-==故3=k ． 解：（二）tan 0000333(tan )tan lim ln 3lim ln 3lim lim3x x k k k x x x x x x x x x xξξξ→→→→---== 33300()tan ln 33ln 3lim ln 3lim 3k k k x x xx o x x x x x x =→→++--==，故3=k ． 例5、设函数)(x f 在0=x 的某邻域内具有一阶连续导数,且,0)0(,0)0(≠'≠f f 若)0()2()(f h bf h af -+在0→h 时是比h 高阶的无穷小,试确定b a ,的值．解： 由条件可知),()0()0()(h h f f h f ο+'+=).()0(2)0()2(h h f f h f ο+'+= 所以)0()2()(f h bf h af -+=).()0()2()0()1(h h f b a f b a ο+'++-+从而⎩⎨⎧=+=-+0201b a b a ,可得⎩⎨⎧-==12b a ．注（1）：设函数)(x f 在0=x 的某邻域内具有n 阶导数，则当0x →时，有 ()(0)()(0)(0)()!n n n f f x f f x x x n ο'=++++ ．证明：()0(0)()[(0)(0)]!lim n nn x f f x f f x x n x→'-+++ ()1'10(0)'()(0)''(0)(1)!lim n n L Hn x f f x f f x x n nx --→'-----= ()2'20(0)''()''(0)(2)!lim (1)n n L Hn x f f x f x n n n x--→----=- (1)(1)()'0()(0)(0)lim !n n n L Hx f x f f x n x --→--== (1)(1)()01()(0)[lim (0)]0!n n n x f x f f n x--→-=-=．注（2）：设函数)(x f 在0=x 的某邻域内具有(1)n +阶导数，利用注（1）的结论，则有()(1)10(0)()(0)(0)(0)!lim (1)!n nn n x f f x f f x xf n x n ++→'---=+ ．例6、设()f x 在0x =处具有二阶导数，且有42260()ln(1)2lim 3x x f x x x x →++-=， 求(0),'(0),''(0)f f f ．解：当0x →时，22''(0)()(0)(0)()2!f f x f f x x x ο'=+++46226ln(1)()23x x x x o x +=-++于是，422602()ln(1)lim 3x x f x x x x →++-=4566601''(0)1[(0)](0)[]()22!3lim x f f x f x x x x ο→'-++++= 201[(0)](0)''(0)12lim []2!3x f f xf x →'-+=++故有1(0),2f ='(0)0f =，而''(0)122!33f +=，即2''(0)3f =．例7、设函数)(x f 在(1,1)-内任意阶可导， ()(0)0n f ≠，1,2,n = ，且满足泰勒公式 (1)()1(0)()()(0)'(0),(1)!!n n n nf f x f x f f x x x n n θ--=++++- (0,1)θ∈，求0lim x θ→．解：()()(1)0()(0)lim (0)0n n n x f x f f xθθ+→-=≠(1)()1()()100(0)(0)()(0)'(0)()(0)(1)!!lim !limn n n nn n n x x f f f x f f x x xf x f n n n x x θ--+→→-------= (1)(1)(0)(0)!(1)!1n n f f n n n ++==++则01lim 1x n θ→=+． 例8、设()f x 在(0,)+∞内满足''()1f x ≤，且lim ()x f x →+∞存在，求证：lim '()0x f x →+∞=．解：当(0,)x ∈+∞时，任取0ε>，有2'()()()'(),(,)2f f x f x f x x x ξεεεξε+=++∈+则()()''()()()''()'()22f x f x f f x f x f f x εξεξεεεε+-+-=-≤+ 1()()2f x f x εεε≤+-+ 注意到lim ()x f x →+∞存在，有1lim '()lim[()()]22x x f x f x f x εεεε→+∞→+∞≤+-+=于是00lim '()lim lim '()lim 02x x f x f x εεε++→+∞→+∞→→=≤=故lim '()0x f x →+∞=．练习题1、设xx x f +-=11)(，则nn n x n x f )1(!2)1()()(+⋅⋅-=． 2、设函数)1ln()(2x x x f +=，则当3≥n ，2!)1()0(1)(--=-n n fn n ． 3、设222xy x y=-，则(2,1)n nz y ∂=∂ 1(1)![1]3nn n +-+．4、设函数()(1)sin f x x x x =-，则(2010)(0)f =2010-．5、计算下列极限（1）0x →=14-（2）0x x →=1（3）30arctan lim ln(12)x x x x →-=+16- （4）0tan 22tan lim sin 33sin x x x x x →-=-12-（5）22201cos lim()sin x x x x →-=43（6）30sin(sin )sin[sin(sin )]lim sin x x x x →-=166、若0)(6sin lim 30=⎥⎦⎤⎢⎣⎡+→x x xf x x ，则206()lim x f x x →+=36． 7、设2)()1l n (lim 220=+-+→x bx ax x x ，则------------------------------------------AA 25,1-==b aB 2,0-==b aC 25,0-==b a D 2,1-==b a8、当0,1cos cos 2cos3x x x x →-对于无穷小x 的阶数为2．9、设当)1(,02++-→bx ax e x x 是比2x 高阶的无穷小，则-------------------------AA 1,21==b aB 1,1==b aC 1,21=-=b a D 1,1=-=b a10、当230,(1)1()x x e ax bx cx o x →++=++是比2x 高阶的无穷小，试确定,,a b c ．121,,633a b c ==-=11、当0,()ln(1)1xx f x ax bx→=-++关于无穷小x 的阶数最高，试确定,a b ．11,2a b ==-12、设)(x f 在0=x 的某邻域内具有二阶连续导数，且0)0(≠f ，0)0(≠'f ，(0)0f ''≠， 求证： 存在惟一的一组实数321,,λλλ，使得当0→h 时，)0()3()2()(321f h f h f h f -++λλλ是比2h 高阶的无穷小．。

泰勒公式百科名片泰勒公式在数学中，泰勒公式是一个用函数在某点的信息描述其附近取值的公式。

如果函数足够光滑的话，在已知函数在某一点的各阶导数值的情况之下，泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值。

泰勒公式还给出了这个多项式和实际的函数值之间的偏差。

目录公式定义证明1.麦克劳林展开式2.麦克劳林展开式的应用泰勒展开式1.原理2.余项泰勒简介1.简介公式定义泰勒公式（Taylor's formula）泰勒中值定理：若函数f(x)在开区间（a，b）有直到n+1阶的导数，则当函数在此区间内时，可以展开为一个关于（x-x.)多项式和一个余项的和：f(x)=f(x.)+f'(x.)(x-x.)+f''(x.)/2!*(x-x.)^2,+f'''(x.)/3!*(x-x.)^3+……+f(n)(x.)/n!*(x-x.)^n+Rn其中Rn=f(n+1)(ξ)/(n+1)!*(x-x.)^(n+1),这里ξ在x和x.之间，该余项称为拉格朗日型的余项。

（注：f(n)(x.)是f(x.)的n阶导数，不是f(n)与x.的相乘。

）证明我们知道f(x)=f(x.)+f'(x.)(x-x.)+α（根据拉格朗日中值定理导出的有限增量定理有limΔx→0 f(x.+Δx)-f(x.)=f'(x.)Δx），其中误差α是在limΔx→0 即limx→x.的前提下才趋向于0，所以在近似计算中往往不够精确；于是我们需要一个能够足够精确的且能估计出误差的多项式：P(x)=A0+A1(x-x.)+A2(x-x.)^2+……+An(x-x.)^n来近似地表示函数f(x)且要写出其误差f(x)-P(x)的具体表达式。

设函数P(x)满足P(x.)=f(x.),P'(x.)=f'(x.),P''(x.)=f''(x.),……,P(n)(x.)=f(n)(x.),于是可以依次求出A0、A1、A2、……、An。

泰勒中值定理公式泰勒中值定理公式简介泰勒中值定理是微积分中的一个重要定理，它表明一个光滑函数在某一点附近可以用一个无穷级数展开，并且展开式中的每一项都与函数在该点的导数有关。

泰勒中值定理在数值计算、函数逼近等领域有重要的应用。

泰勒公式泰勒公式可以写作以下形式：f(x)=f(a)+f′(a)(x−a)+f″(a)2!(x−a)2+f‴(a)3!(x−a)3+⋯+f(n)(a)n!(x−a)n+R n(x)其中，f(x)是要展开的函数，a是展开点，f(n)(a)表示函数f(x)在点a处的n阶导数。

R n(x)是一个余项，表示剩余部分。

一阶泰勒展开一阶泰勒展开是泰勒公式的特殊情况，当n=1时，泰勒公式可以简化为：f(x)=f(a)+f′(a)(x−a)+R1(x)这个公式表示了函数f(x)在点a处的一阶近似。

举个例子，考虑函数f(x)=sin(x)在点a=0处展开。

根据一阶泰勒展开公式，我们有：sin(x)=sin(0)+cos(0)(x−0)+R1(x)化简得：sin(x)=x+R1(x)这表示在原点附近，sin(x)可以近似为x。

二阶泰勒展开二阶泰勒展开是泰勒公式的下一个级别，当n=2时，泰勒公式可以简化为：f(x)=f(a)+f′(a)(x−a)+f″(a)2!(x−a)2+R2(x)这个公式表示了函数f(x)在点a处的二阶近似。

举个例子，考虑函数f(x)=cos(x)在点a=0处展开。

根据二阶泰勒展开公式，我们有：cos(x)=cos(0)+sin(0)(x−0)+−cos(0)2!(x−0)2+R2(x)化简得：cos(x)=1−12x2+R2(x)这表示在原点附近，cos(x)可以近似为1−12x2。

高阶泰勒展开泰勒展开还可以一直延伸到更高阶。

当n很大时，泰勒展开可以越精确地近似函数。

但需要注意的是，高阶泰勒展开的计算相对复杂，因此常常只会取前几阶展开项来近似。

总结： - 一阶泰勒展开：f(x)≈f(a)+f′(a)(x−a) - 二阶泰勒展开：f(x)≈f(a)+f′(a)(x−a)+f″(a)2!(x−a)2以上是针对泰勒中值定理公式的简要介绍和示例解释。

泰勒公式与泰勒中值定理的系统理论与使用技巧泰勒公式（Taylor's theorem）和泰勒中值定理（Taylor's theorem with remainder）是微积分中重要的定理，用于用已知函数的其中一点的信息推导出该函数在附近任意点的近似值。

下面将对这两个定理的系统理论和使用技巧进行详细阐述。

1. 泰勒公式（Taylor's theorem）：泰勒公式是一个逼近函数的公式，其形式如下：f(x)=f(a)+f'(a)(x-a)+f''(a)(x-a)^2/2!+f'''(a)(x-a)^3/3!+...其中，f(x)是要逼近的函数，a是近似点，f'(a)、f''(a)、f'''(a)等是函数在点a的各阶导数。

公式可以继续扩展至更高阶导数。

泰勒公式的推导涉及到多项式的展开，通过使用导数的定义进行求解，存在其中一种程度的复杂性。

然而，在实际应用中，我们通常使用该公式的前几项进行近似计算，而不需要考虑无穷多项的求和。

在使用泰勒公式时，需要满足以下条件：-要求函数f(x)在开区间(a,b)上具有至少n+1阶连续导数；-近似点a必须在开区间(a,b)内；-近似点a必须在函数f(x)在(a,b)范围内的一些点，即a∈(a,b)。

2. 泰勒中值定理（Taylor's theorem with remainder）：泰勒中值定理是泰勒公式的一个推广，它包含了一个误差项。

泰勒中值定理的形式如下：f(x)=f(a)+f'(a)(x-a)+f''(a)(x-a)^2/2!+...+f^n(a)(x-a)^n/n!+R_n(x)其中，R_n(x)是余项，它表示在使用泰勒公式展开的前n项进行近似时产生的误差。

余项的具体形式为：R_n(x)=(x-a)^n/(n!)*(f^(n+1)(c))其中，c是a和x之间的一些点。

泰勒公式与导数的应用名称主要内容泰勒中值定理：如果f ( x) 在含有x 0 的某个开区间( a,b) 内具有n1阶的导数，则对任一x (a,b) ，有 f (x) f (x0 ) f / (x0 )( x x0) f //2(!x0 )(xx0)20 2!f (n) (x0) n(x x0) R n( x) ，此公式称为n 阶泰勒公式；n!f (n 1)( )n 1其中R n (x) (x x 0) ( 介于x0 于x 之间)，称为拉格朗日型余或泰(n 1)!R n(x) o[( x x0)n ] ，称为皮亚诺型余项。

勒n 阶麦克劳林公式：f (x) f (0) f/(0)x f //(0) x2 f (n)(0) x nx R n(x)2! n!公其中R n ( x) ( n 1)f ( x) n 1 x(0 1)或R n(x) o(x n ) 。

(n 1)!式常用的初等函数的麦克劳林公式：1)e x12x x n xo(x n) 2! n!35 2n 12) sin x x xx (n x 2n 2 )1) o( x3! 5! (2n 1)!246 2n3) cos x 1 xxx n x2n 1)( 1) n o(x2n2! 4! 6! (2n)!23xx x ( 1)n x n14) ln(1 x) n1o(x n1)23 n 15) 11x 12x x x n o(x n)1xm 6) (1 x)m(m1 mx1) 2 m( m 1) ( m n 1) nn)x n! x o( x2!13x巩固练习★1.按(x 1)的幂展开多项式 f (x) x 4 3x 2 4。

知识点 ：泰勒公式。

思路：直接展开法。

求 f (x) 按(x x 0 )的幂展开的 n 阶泰勒公式，则依次求 f ( x) 直到 n 1 阶的导 数在 xx 0 处的值，然后带代入公式即可f (1) 10 ； f (x) 12x 2 6， f (1) 18；将以上结果代入泰勒公式，得介于 x 与 4之间)知识点 ：麦克劳林公式。

1第三节泰勒(Taylor)公式问题的提出 泰勒中值定理简单应用2一、问题的提出例如 取x 0=0, 当x 很小时, x e x+≈1 , xx ≈+)1ln(（如下图）在微分中我们讲过，当很小时，||x Δ),(x o dy y Δ+=Δ即,)(x x f y Δ′≈Δ令：则,0x x x −=Δ),)((')()(000x x x f x f x f −+≈误差为.|)(|0x x o −上式表明函数f (x )在x 0的附近可用一个线性函数来近似。

且当很小时，误差||0x x −,)()()()(001x x f x f x f x R Δ′−−=也很小。

3xy +=1oxey =oxy =)1ln(x y +=4进一步的问题是：1) 线性近似的误差R 1(x)，如何估计？2)线性近似的理论依据是Δy ≈dy ，几何上意味着在用切线代替曲线，即“以直代曲”，显然精度不够，如何改进能提高局部近似的精度？下面来解决这两个问题。

.0lim ,)]()(21[)(02001=α−α+′′=→x x x x x f x R 由洛必达法则及极限与无穷小的关系，知)])(()([)()(:0001x x x f x f x f x R −′+−=记误差1）),)(()()(000x x x f x f x f −′+≈误差为.|)(|0x x o −5200000))((21))(()()(x x x f x x x f x f x f −′′+−′+≈3020)]()(!31[x x x f −α+′′′=]))((21))(()([)()(2000002x x x f x x x f x f x f x R −′′+−′+−=误差300200000))((!31))((21))(()()(x x x f x x x f x x x f x f x f −′′′+−′′+−′+≈因此]))((!31))((21))(()([)()(3002000003x x x f x x x f x x x f x f x f x R −′′′+−′′+−′+−=误差4030)]()(!41[x x x f −α+′′′=2) 提高多项式的次数来改进精度6由此分析看出，随着多项式函数的阶数的提高，这一特殊类型的多项式与函数f (x )的近似程度越好。