刚体的复合运动

刚体旋转知识点归纳总结1. 刚体旋转的基本概念刚体是指在一定时间内，其内部各点的相对位置不改变的物体。

刚体旋转是指刚体围绕固定点或固定轴发生的旋转运动。

在刚体旋转中，需要引入一些基本概念：1.1 刚体的转动刚体的旋转可以是定点转动，也可以是定轴转动。

在定点转动中，刚体绕固定点旋转，而在定轴转动中，刚体绕固定轴旋转。

定点转动和定轴转动都是刚体旋转运动的两种基本形式。

1.2 刚体的转动角度和角速度刚体的转动角度是刚体在单位时间内所转过的角度，通常用θ表示。

刚体的角速度是指刚体单位时间内转过的角度，通常用ω表示。

在刚体定点转动中，角速度是刚体绕定点旋转的角度速度；在刚体定轴转动中，角速度是刚体绕定轴旋转的角度速度。

1.3 刚体的转动惯量刚体的转动惯量是衡量刚体抵抗旋转的惯性大小，通常用I表示。

刚体转动惯量的大小取决于刚体形状、质量分布以及旋转轴的位置。

对于质点组成的刚体，其转动惯量可以通过对质点的质量进行积分得到。

1.4 刚体的角动量刚体的角动量是刚体旋转运动的物理量，通常用L表示。

角动量的大小和方向分别由角速度和转动惯量决定。

在定点转动中，如果刚体的角速度和转动惯量都不变，那么刚体的角动量也保持不变；在定轴转动中，如果刚体绕固定轴旋转，那么刚体的角动量也保持不变。

2. 刚体的转动力学刚体的转动力学研究刚体在旋转运动中所受的力和力矩，包括转动定律、角动量定理、动能定理等内容。

2.1 刚体的平衡刚体旋转平衡需要满足一定的条件，包括力矩平衡条件和动量平衡条件。

刚体力矩平衡条件是指刚体所受的合外力矩为零；刚体动量平衡条件是指刚体所受的合外力矩关于某一点的力矩为零。

2.2 刚体的角动量定理刚体的角动量定理描述了刚体在受到外力矩作用下，其角动量的变化规律。

根据角动量定理，刚体所受外力矩产生的角动量变化率等于刚体所受外力矩的矢量和。

2.3 刚体的动能定理刚体的动能定理描述了刚体在旋转运动中，其动能的变化规律。

根据动能定理，刚体所受外力矩产生的功率等于刚体动能的变化率。

刚体运动的基本原理刚体运动是物体在空间中做整体性的运动，不发生形变的运动。

刚体运动的基本原理可以通过以下几个方面来解释：一、质点的运动质点可以看作是质量无限大的一个点，它不发生形变，仅产生平移运动。

质点的平移运动可以用牛顿第一定律来描述，即物体在不受外力作用时将保持静止或者匀速直线运动。

这是因为质点不受力的影响，所以它的速度和位置都不会改变。

二、刚体的自由度刚体在空间中的运动由其自由度决定。

自由度是指刚体能够独立运动的最小数量。

对于一个刚体而言，它的自由度取决于它的维度。

在三维空间中，一个刚体有6个自由度，分别为三个平移自由度和三个转动自由度。

三、刚体的平移运动刚体的平移运动是指它在空间中沿着直线运动，整体上保持不变。

刚体的平移运动可以由质点的运动来描述。

当一个刚体受到一个外力时，该外力会作用在刚体的重心上，使得刚体产生平移运动。

刚体的平移加速度与作用在刚体上的合力成正比，与刚体的质量成反比。

四、刚体的转动运动刚体的转动运动是指它在空间中绕轴线旋转，整体上保持不变。

刚体的转动运动可以由刚体的转动惯量来描述。

转动惯量是刚体旋转惯性的量度，与刚体的质量分布以及轴线的位置有关。

当一个刚体受到一个力矩时，该力矩会使刚体产生转动运动。

刚体的转动加速度与作用在刚体上的合力矩成正比，与刚体的转动惯量成反比。

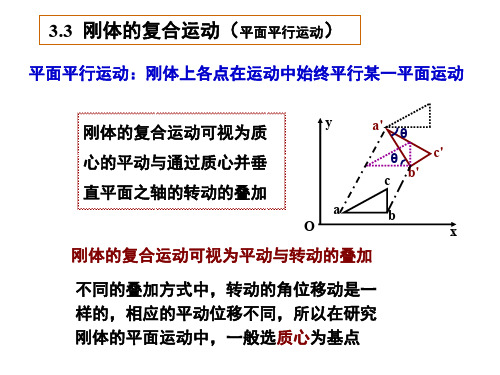
五、刚体的复合运动刚体可以进行平移和转动的复合运动。

当一个刚体受到既有平移又有转动的外力时，刚体既会发生平移运动，也会发生转动运动。

刚体的平移和转动是相互独立的，但它们会同时发生。

六、刚体碰撞的基本原理当两个刚体碰撞时，根据动量守恒定律和动能守恒定律，可以得到碰撞前后刚体的动量和动能之间的关系。

在完全弹性碰撞中，刚体在碰撞过程中既满足动量守恒定律，也满足动能守恒定律。

在非完全弹性碰撞中，刚体在碰撞过程中会发生能量损失，动能不守恒。

总结：刚体运动的基本原理包括质点的运动、刚体的自由度、刚体的平移和转动运动，以及刚体碰撞的原理。

刚体力学的基本性质与运动分析刚体力学是物理学中的一个重要分支，研究物体的运动和力学性质。

它假设物体是刚性的，即不会发生形变。

在刚体力学中，有一些基本性质和运动分析方法，本文将对这些内容进行探讨。

一、刚体的基本性质刚体是指在力的作用下不会发生形变的物体。

它的基本性质有三个：质点性、形状不变性和刚性。

质点性是指刚体可以看作一个质点，即物体的大小和形状对其运动没有影响。

这意味着刚体的运动可以通过描述质心的运动来表示。

形状不变性是指刚体在运动过程中，其形状保持不变。

无论刚体如何运动，其各个部分之间的距离和角度都保持不变。

刚性是指刚体内部各个点之间的相对位置保持不变。

这意味着刚体的任意两点之间的距离和角度在运动过程中保持不变。

二、刚体的运动分析方法在刚体力学中，有几种常用的运动分析方法，包括平动、转动和复合运动。

平动是指刚体的各个部分在同一时间内以相同的速度和方向运动。

在平动中，刚体的质心和各个部分的速度和加速度都相同。

转动是指刚体绕某个轴线旋转。

在转动中，刚体的各个部分围绕轴线旋转，但质心保持静止。

复合运动是指刚体同时进行平动和转动。

在复合运动中，刚体的质心同时进行平动，而各个部分围绕质心旋转。

为了描述刚体的运动，我们可以使用刚体的运动学方程和动力学方程。

运动学方程描述了刚体的位置、速度和加速度之间的关系，而动力学方程描述了刚体的受力和运动之间的关系。

在运动分析中，我们还可以使用刚体的转动惯量和角动量来描述刚体的运动特性。

转动惯量是刚体对转动的惯性度量，它与刚体的质量和形状有关。

角动量是刚体的旋转运动的物理量，它与刚体的转动惯量和角速度有关。

三、刚体力学的应用刚体力学在工程和科学研究中有广泛的应用。

在工程中，刚体力学可以用于分析建筑物和桥梁的结构强度和稳定性。

它还可以用于设计机械装置和运动控制系统。

在科学研究中，刚体力学可以用于研究天体运动和分析地震运动。

它还可以用于研究分子和原子的运动和相互作用。

总之，刚体力学是物理学中的一个重要分支，研究物体的运动和力学性质。

刚性知识点总结一、刚体的基本概念1. 刚体的定义刚体是指在外力作用下不产生形变的物体。

在力学中，理想的刚体是不允许发生形变的，但实际上在受力的作用下，任何物体都会产生微小的形变。

所以，严格地说，真正意义上的刚体是不存在的。

但在研究刚体的运动规律时，可以假设物体是刚体。

2. 刚体的性质a. 刚体的质点性：刚体可以看作由无限多个质点组成的系统，因此刚体也具有质点的性质。

b. 刚体的自由度：刚体的自由度是指刚体固定在空间中的位置所需要的独立坐标的数量。

对于平动刚体（即只进行平移运动的刚体），其自由度为3；对于转动刚体（即只进行转动运动的刚体），其自由度为3；而对于一般的刚体来说，其自由度为6。

3. 刚体的平移运动与旋转运动刚体的运动可以分为平移运动和旋转运动两种。

平移运动是指刚体的中心沿直线运动，而旋转运动是指刚体围绕某一固定轴进行转动。

刚体的平移运动和旋转运动可以同时发生，即平移运动和旋转运动可以叠加在一起。

二、刚体的运动1. 刚体的平动运动刚体的平移运动是指刚体的中心围绕其质心作直线运动。

在平移运动中，刚体上的任何一点都以相同的速度移动。

根据牛顿第二定律，刚体的平移运动与质心处的合外力成正比，与刚体的总质量成反比。

2. 刚体的旋转运动刚体的旋转运动是指刚体的不同部分围绕刚体固定的轴（称为旋转轴）作圆周运动。

在旋转运动中，刚体上的各点围绕旋转轴作圆周运动，速度和加速度不同。

刚体的旋转运动可分为定轴运动和自由转动两种情况。

3. 刚体的复合运动刚体的运动通常是复合的，即同时包括平移运动和旋转运动。

在复合运动中，刚体的平移运动和旋转运动是相互耦合的，即平移运动会影响旋转运动，而旋转运动也会影响平移运动。

三、刚体的力学平衡1. 刚体的平衡条件刚体的力学平衡是指刚体在外力作用下静止或保持匀速直线运动的状态。

在静力学中，刚体的平衡条件包括平衡力的条件和力矩的条件两种。

平衡力的条件是指刚体所受的合外力为零，力的合力矩的条件是指刚体所受的合外力矩为零。

刚体的运动和转动刚体是指物体在运动或转动过程中，各部分之间保持相对位置不变的物体。

在物理学中，刚体是一个重要的概念，它的运动和转动具有一定的规律和性质。

本文将详细探讨刚体的运动和转动，以及相关的基本概念和原理。

一、刚体的运动刚体的运动是指整个物体的平动，即物体作为一个整体的运动。

平动可以是沿直线运动，也可以是曲线运动。

根据牛顿第一定律，当物体所受合外力的矢量和为零时，物体将保持静止或匀速直线运动。

而当物体所受合外力的矢量和不为零时，物体将发生加速度，即产生直线运动。

刚体的平动可以通过理解质点来进行分析。

质点是指物体的质量集中在一个点上，没有形状和大小，无论是刚体还是非刚体，都可以看作是由许多质点组成的。

因此，在分析刚体的平动时，可以把刚体简化为质点。

同时，刚体的平动也满足牛顿第二定律，即合外力等于质量乘以加速度。

二、刚体的转动刚体的转动是指物体绕某个轴进行旋转的运动。

转动的轴可以是任意选择的，但通常选择物体上的某个固定点或固定轴线作为转动的轴。

在刚体的转动中，每一个点都绕轴线进行圆周运动，并且所有点的转动角度相等。

刚体的转动可以由物体的转动惯量和转动力矩来描述。

转动惯量是物体对转动的抵抗程度或者旋转惯性的量度，它与物体的质量分布和形状密切相关。

转动力矩则是引起刚体转动的力和力臂的乘积，它的方向由右手定则给出。

根据角动量守恒定律，当刚体不受外力矩作用时，刚体的角动量守恒。

这意味着刚体的角动量大小和方向在运动过程中保持不变，从而导致刚体产生转动。

三、刚体的动力学方程刚体的运动和转动都可以通过动力学方程来描述。

对于平动的刚体，动力学方程可以表示为：∑F = ma其中，∑F表示物体所受合外力的矢量和，m表示物体的质量，a表示物体的加速度。

而对于转动的刚体，动力学方程可以表示为：∑τ = Iα其中，∑τ表示物体所受合外力矩的矢量和，I表示刚体的转动惯量，α表示刚体的角加速度。

四、刚体的运动和转动的实例刚体的运动和转动在日常生活和工程领域中有着广泛的应用。