二面角和二面角的平面角
- 格式:ppt
- 大小:540.00 KB
- 文档页数:10

二面角平面角的几种求法作者:吕秀娟来源:《中国校外教育·基教(中旬)》2014年第03期介绍了二面角,二面角的平面角的定义和二者的关系,三垂线定理及其逆定理,并重点给出了求二面角平面角的六种方法。
立体几何二面角平面角求法空间图形的位置关系是立体几何的重要内容,在面面关系中,二面角是其中的主要概念之一,它的计算归结为平面角的计算.一般来说,对其平面角的定位是问题解决的先决一步,由于二面角的平面角是由一点和两条射线构成,所以二面角的平面角的定位可化归为“定点”“定线”或“定面”的问题,在做题时只需分别找“点”“垂线”或“垂面”.事实上,只要找到其中一个,另外两个就会接踵而来,掌握这一点对提高解题技能和培养空间想象力非常重要。
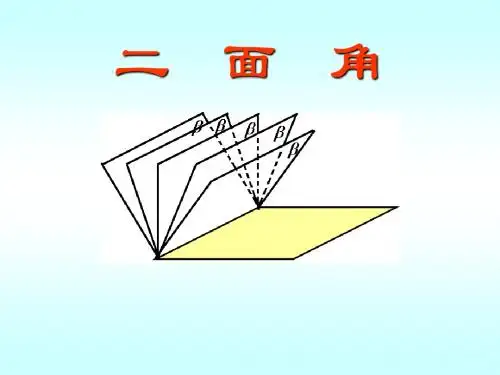
一、预备知识平面内的一条直线把平面分为两部分,其中的每一部分都叫做半平面,从一条直线出发的两个半平面所组成的图形,叫做二面角。
(这条直线叫做二面角的棱,每个半平面叫做二面角的面)。
以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所组成的角叫做二面角的平面角。
二面角的大小就是用它的平面角来度量,二面角的平面角的数值大小就等于二面角的大小。
定理1(三垂线定理):在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
定理2(三垂线定理的逆定理):在平面内的一条直线,如果它和这个平面的一条斜线垂直,那么它也和这条直线在平面内的射影垂直。
二、二面角平面角的大小的求法1.定义法在二面角的棱上找一特殊点,在两个半平面内分别作垂直于棱的垂线,如图1所示。
用定义法求二面角的平面角时,首先需要根据二面角的定义把它转化为平面角,然后把这个平面角置于一个三角形中,通过解三角形求二面角,其基本的解题步骤为“一作,二证,三求”。
2.垂射线法即垂面法过棱上一点作棱的垂直平面,该平面与二面角的两个半平面的交线组成的角即为二面角的平面角,如图2所示,∠AOB为二面角的平面角。


二面角及其平面角[引言]二面角相关问题的求解是必修二立体几何中的难点,也是许多同学较为头疼的问题.本文则主要讲解二面角类问题的常用解法.[概念]由一条直线出发的两个半平面组成的图形(或:一个半平面以其边界为轴旋转而成为图形)叫做二面角.直线叫做二面角的棱,半平面叫做二面角的面.图1 二面角ɑ-l-β由半平面ɑ-直线l-半平面β构成[二面角的度量]以二面角棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.二面角的平面角的三个特征:1、点在棱上2、线在面内3、与棱垂直二面角的平面角的大小范围:0°≤θ≤180°平面角是90°的二面角叫做直二面角[二面角的平面角作法]做出二面角的平面角是运用几何方法求解二面角问题的关键,这里笔者提供找平面角的三种方法供同学们参考1、定义法:此法适用于过棱上一点找平面角.过二面角棱上一点P作平面ɑ内一条直线AP与平面β内一条直线BP分别与棱l垂直,则∠APB即为二面角ɑ-l-β的平面角.2、三垂线(逆)定理法:此法适用于过面上一点找平面角.过平面β上一点P作PA⊥ɑ于A,再过A作AB⊥棱l于B,连接BP.易证平面ABP⊥l,故∠APB即为二面角ɑ-l-β的平面角3、垂面法:此法适用于过二面角内一点找平面角.过二面角内一点P分别作平面ɑ、β的垂线PA、PB,连接B、O、A.易证平面PBOA⊥l,故∠APB即为二面角ɑ-l-β的平面角图2 二面角的平面角的三种作法[例题1]已知锐二面角ɑ-l-β,A为ɑ内一点,A到β的距离为2√3,到l距离为4,求二面角ɑ-l-β的大小此例题较简单,通过这个题我们可以将二面角的求法可以归纳为以下三步:1、找到或作出题目中二面角的平面角2、证明1中的角为所求二面角3、计算出角的大小一“作”二“证”三“计算”下面给出参考解法解:过A作AO⊥ɑ于O,过O作OD⊥l于D,连结AD.(对应1)由三垂线定理得AD⊥l∴∠ADO即为二面角ɑ-l-β的平面角(对应2)∵AO为A到β的距离,AD为A到l的距离∴AO=2√3,AD=4在Rt△ADO中∴sin∠ADO=√3/2∵二面角的范围是[0,π]故∠ADO=60°即二面角ɑ-l-β的大小为60°(对应3)需要注意的是,有时题目中并不直接给出点到平面的距离,此时点到平面的距离通常要用到简单几何体的体积或勾股定理求出.[思考]如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.若PA=1,AD=2,试求二面角B-PC-A的正切值. 点拨:不妨证明BD⊥平面PAC,或利用面积法求出点到平面的距离.[拓展延伸]以下内容供有余力的同学参考面积射影定理:“平面图形射影面积等于被射影图形的面积S乘以该图形所在平面与射影面所夹角的余弦.”S射影面积=S原图形面积×cosθ即cosθ=S射影图/S原图(平面多边形及其射影的面积分别是S原,S射影,它们所在平面所成锐二面角的为θ)证明思路:因为射影就是将原图形的长度(三角形中称高)缩放,所以宽度是不变的,又因为平面多边形的面积比=边长的平方比.所以就是图形的长度(三角形中称高)的比.那么这个比值应该是平面所成角的余弦值.在两平面中作一直角三角形,并使斜边和一直角边垂直于棱(即原多边形图的平面和射影平面的交线),那么三角形的斜边和另一直角边就是其多边形的长度比,即为平面多边形的面积比,而将这个比值放到该平面三角形中去运算,即可.运用这一方法可以解决求无棱二面角的大小问题,关键是从图中找出斜面多边形和它在有关平面上的射影(即找到从一个面内一点向另一面的垂线)通常求两个面内的三角形的面积比较容易.。

《二面角垂直向量角与二面角的平面角相等或互补的关系》一、引言二面角是我们在几何学习中经常接触到的概念,它是一个重要的几何性质。
在这篇文章中,我们将以“二面角垂直向量角与二面角的平面角相等或互补的关系”为主题,深入探讨其性质和关联,以便更好地理解几何学的重要概念。
二、二面角垂直向量角的性质在几何学中,二面角是指由两条射线(或直线段)构成的角。
当这两条射线(或直线段)相交时,它们将平面分为两个部分,并形成一个有向角,我们称之为二面角。
在此基础上,我们引入了二面角的垂直向量角的概念。
二面角的垂直向量角是指与二面角拥有公共边且顶点重合的另一个二面角,这两个二面角的垂直向量角的性质是非常特殊的。
二面角的垂直向量角相等。
这意味着当两个二面角的垂直向量角相等时,它们所构成的二面角也是相等的。
这是一个非常重要的性质,它为我们在几何推导和证明过程中提供了重要的依据。
二面角的垂直向量角互补。
这意味着当两个二面角的垂直向量角之和为直角时,它们所构成的二面角也是互补的。
这个性质在几何学的证明和推导中也有着重要的应用。
三、二面角的平面角的性质除了二面角的垂直向量角,我们还需要了解二面角的平面角。
二面角的平面角是指在同一个平面内,以相同的顶点为端点的两个相邻的二面角的非公共边所成的角。
二面角的平面角也具有一些特殊的性质,与二面角的垂直向量角有着一定的关联。
二面角的平面角相等。
这意味着当两个相邻的二面角的平面角相等时,它们所构成的二面角也是相等的。
二面角的平面角互补。
这意味着当两个相邻的二面角的平面角之和为直角时,它们所构成的二面角也是互补的。
通过这些性质,我们可以更好地理解二面角在平面几何中的特殊作用,以及其在证明和推导中的应用。
四、个人观点和总结回顾通过对二面角垂直向量角和平面角的性质深入探讨,我们能够更好地理解几何学中重要的概念和性质。
二面角的垂直向量角和平面角的相等或互补关系,在几何证明和推导中具有重要的作用,它为我们提供了重要的几何依据和工具。


第6课时二面角(一)●要点·疑点·考点●课前热身●能力·思维·方法●延伸·拓展●误解分析要点·疑点·考点1. 二面角的定义:从一条直线出发的两个半平面所组成的图形,叫二面角,其大小通过二面角的平面角来度量.2.二面角的平面角:(1)定义:以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.(2)范围:[0,π ]2.如图,正方体ABCD —A 1B 1C 1D 1中,二面角B 1-AA 1-C 1的大小为_____,二面角B-AA 1-D 的大小为______,二面角C 1-BD-C 的正切值是_______.245°90°能力·思维·方法1.在三棱锥S—ABC中,SA⊥平面ABC,AB⊥BC,DE 垂直平分SC,且分别交AC、SC于D、E,又SA=AB= a,BC=2a,(1)求证:SC⊥平面BDE;(2)求平面BDE与平面BDC所成的二面角大小.【解题回顾】本题是1990年全国高考题,(1)的证明关系较复杂,需仔细分析。
(2)的平面角就是∠CDE,很多考生没有发现,却去人为作角,导致混乱.2.已知斜三棱柱ABC—A1B1C1中,∠BCA=90°,AC= BC,A1在底面ABC的射影恰为AC的中点M.又知AA1与底面ABC所成的角为60°.(1)求证:BC⊥平面AA1C1C;(2)求二面角B-AA1-C的大小.3.如图,正三棱柱ABC —A 1B 1C 1的底面边长为a ,侧棱长为,若经过对角线AB 1且与对角线BC 1平行的平面交上底面一边A 1C 1于点D.(1)确定点D 的位置,并证明你的结论;(2)求二面角A 1-AB 1-D 的大小.a 22【解题回顾】第(2)题中二面角的放置属于非常规位置的图形(同例(1)的变题),看起来有些费劲,但是一旦将图形的空间位置关系看明白,即可发现解决此种问题的基本方法仍然与常规位置时相同.延伸·拓展4.如图,已知A1B1C1—ABC是正三棱柱,D是AC的中点.(1)证明AB1∥平面DBC1.(2)假设AB1⊥BC1,求以BC1为棱,DBC1与CBC1为面的二面角α的度数.误解分析1.二面角是立体几何的重点、热点、难点,求二面角的大小方法多,技巧性强.但一般先想定义法,再想三垂线定理法,如课前热身4,及能力•思维•方法1中,如果盲目作垂线,则会干扰思维.2.实施解题过程仍要注意“作、证、指、求”四环节,计算一般是放在三角形中,因此,“化归”思想很重要.。

北京四中撰稿:涂小琴编审:涂小琴责编:严春梅二面角[本周重点] 二面角的概念[本周难点]二面角的平面角[本周内容]一、二面角:从一条直线出发的两个半平面所组成的图形叫做二面角。
二面角的平面角:以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
二、二面角的平面角画法:1.定义法:如图1,以棱上一点O为端点在两个面内分别作垂直于棱的两条射线组成平面角;2.垂面法:如图2,经过棱上一点O画垂直于棱的平面与两个面的交线组成平面角;3.垂线法:如图3,设A在二面角α-l-β的半平面α内,作AH⊥平面β,H为垂足,在平面β内作HB⊥l,HB∩l=O,连结AO,则∠AOB是二面角的平面角;4.垂点法:如图4,设P是二面角α-l-β内部一点,作PA⊥面α,PB⊥面β,A、B 是垂足,在面α内,作AD⊥l于D,连结DB,则∠ADB是二面角α-l-β的平面角。
5.如图5,求二面角的大小也可不必作出二面角的平面角,求出β内一个图形的面积S和它在α上射影图形面积S′,由公式,可求二面角余弦值进而求其大小。
三.用向量求二面角的大小方法1:转化为分别是在二面角的两个半平面内且与棱都垂直的两条直线上的两个向量的夹角(注意:要特别关注两个向量的方向).方法2:先求出二面角一个面内一点到另一个面的距离及到棱的距离,然后通过解直角三角形求角.方法3:(法向量法)、分别是平面和平面的法向量,那么<,>(或者其补角)与二面角-l-的大小相等。
方法4:公式S′=Scos.如果平面多边形所在平面与平面所成角为,这个平面多边形及其在平面内的射影的面积分别为S、S′,那么S′=Scos.典型题目例1.在正方体ABCD-A1B1C1D1中,E、F分别是AB、C1D1的中点,求平面EB1FD与ADD1A1所成的二面角的余弦值。
解:如图所示,以D为坐标原点建立空间直角坐标系D-xyz,设正方体边长为2则D(0,0,0),E(2,1,0),F(0,1,2),从而=(2,1,0),=(0,1,2),且=(0,1,0)是平面ADD1A1的法向量设平面EB1FD的法向量是=(x,y,z),则⊥,⊥,因此•=0,•=0,即,令z=1得:x=1,y=-2,所以=(1,-2,1),因此cos<,>==,因此<,>=arccos(),∵平面EB1FD与ADD1A1所成的二面角是一个锐角,所以平面EB1FD与ADD1A1所成的二面角的余弦值为.点评:本题利用组成二面角的两面的法向量所成的角(或其补角)求解二面角问题.例2.如图,在四面体ABCD中,AB⊥平面BCD,BC=CD,∠BCD=90°,∠ADB=30°.E、F分别是AC,AD的中点.(1)求证:平面BEF⊥平面ABC;(2)求平面BEF和平面BCD所成的角.分析:证明两个平面互相垂直,就是要证明一个平面过另一个平面的一条垂线,这样就需证明一直线与平面上两相交直线垂直,而证明两直线互相垂直,证明向量的数量积为0就可以了.解:(1)建立如图所示的空间直角坐标系,取A(0,0,a). 由∠ADB=30°可得:B(0,0,0),. ∴∵∴EF⊥AB, EF⊥BC.∴EF⊥平面ABC,又EF平面BEF∴平面BEF⊥平面ABC.(2)作EE′⊥BC于E′,,作FF′⊥BD于F′,,,显然,∴BE⊥EF∴,,∴∴∴,即平面BEF和平面BCD所成的角为.点评:利用判定定理结合向量运算证面面垂直是本例的特点之一.这种方法十分重要,应予掌握. 例3.在正四面体ABCD中,AD=1(1)求AD与平面BCD所成的角;(2)求相邻两个面所成的二面角.解:(1)如图,因为四面体ABCD是正四面体,所以A在底面BCD的射影是底面三角形BCD的中心O,延长DO交BC于E,E是BC的中点,∴∠ADE就为AD与平面BCD所成的角q∴,又,∴∴.∴AD与平面BCD所成的角;(2)在ΔAED中,因为E是BC的中点,所以AE⊥BC,DE⊥BC,所以∠AED就是二面角A-BC-D的平面角a.又.∴,∴.∴相邻两个面所成的二面角是.点评:本例系常规题型,要掌握这类题目的解法.例4.如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(1)求MN的长;(2)求a为何值时,MN的长最小;(3)当MN长最小时,求面MNA与面MNB所成的二面角的大小。

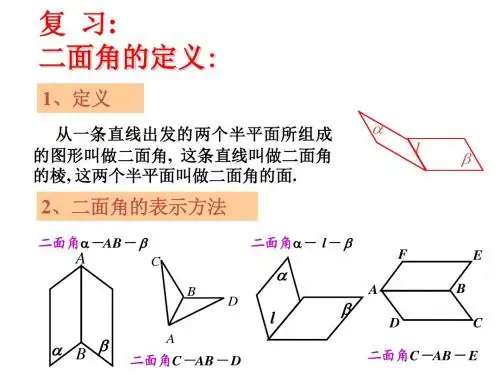
二面角的平面角及求法1、半平面的定义:一条直线把平面分成两个部分,每一部分都叫做半平面.2、二面角的定义:从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面。
3、二面角的平面角的概念:以二面角的棱上任意一点为顶点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫二面角的平面角。
一个平面角的大小可用它的平面的大小来衡量,二面角的平面角是多少度,就说这个二面角是多少度。
二面角大小的取值范围是[0,180°]。
4、直二面角:平面角是直角的二面角叫直二面角。
两相交平面如果所组成的二面角是直二面角,那么这两个平面垂直;反过来,如果两个平面垂直,那么所成的二面角为直二面角。
5、二面角的平面角具有下列性质:a.二面角的棱垂直于它的平面角所在的平面,即l⊥平面AOB.b.从二面角的平面角的一边上任意一点(异于角的顶点)作另一面的垂线,垂足必在平面角的另一边(或其反向延长线)上.c.二面角的平面角所在的平面与二面角的两个面都垂直,即平面AOB⊥α,平面AOB⊥α.6、求二面角的平面角的方法:(1)定义法:通过二面角的平面角来求;找出或作出二面角的平面角;证明其符合定义;通过解三角形,计算出二面角的平面角.上述过程可概括为一作(找)、二证、三计算”.(2)三垂线法:已知二面角其中一个面内一点到另一个面的垂线,用三垂线定理或其逆定理作出平面角.(3)垂面法:已知二面角内一点到两个面的垂线时,过两垂线作平面与两个半平面的交线所成的角即为平面角,由此可知,二面角的平面角所在的平面与棱垂直.(4)射影法:利用面积射影定理求二面角的大小;其中S为二面角一个面内平面图形的面积,S′是这个平面图形在另一个面上的射影图形的面积,α为二面角的大小.(5)向量法:设二面角的平面角为θ.①如果那么②设向量m、n分别为平面α和平面β的法向量是相等还是互补,根据具体图形判断。
二面角和两平面角的范围
1.二面角的范围:
二面角是指两个不共面的平面的交角。
它的范围是0度到
180度(开区间)。
具体来说,当两个平面相互平行时,二面
角为0度;当两个平面相互垂直时,二面角为90度;当两个
平面夹入一个锐角时,二面角为锐角的度数(大于0小于90度);当两个平面夹入一个钝角时,二面角为钝角的补角的度
数(大于90度小于180度)。
2.两平面角的范围:
两平面角是指由两个平面相交而形成的角。
它的范围是0度
到360度(开区间)。
具体来说,当两个平面完全平行时,两
平面角为0度;当两个平面相互垂直时,两平面角为90度或270度(与顺逆时针方向有关);当两个平面夹入一个锐角时,两平面角的度数为锐角的补角的度数(相当于两个二面角的和);当两个平面夹入一个钝角时,两平面角的度数为钝角的
度数加上180度(相当于两个二面角的差)。
需要注意的是,二面角和两平面角的度数虽然有限制范围,
但可以通过具体的几何情况来确定其具体大小。
这些角度范围
的理解有助于我们在几何推导和计算中正确地应用它们。
立体几何中二面角的平面角的定位【摘要】立体几何中的二面角是一个重要的概念,而平面角的定位在二面角中有着特殊的作用。
本文首先介绍了二面角和平面角的基本概念,然后探讨了二面角的特性和分类。
接着重点讨论了二面角的平面角的定位问题,并探讨了平面角与二面角之间的关系。
我们详细阐述了平面角的测量方法。
通过深入理解平面角的定位,我们可以更好地解决立体几何中的问题,提高解题效率。
掌握平面角的定位对于学习立体几何具有重要意义,可以帮助我们更好地理解立体几何中的概念和定理,解决相关问题。
【关键词】二面角、平面角、定位、立体几何、特性、分类、关系、测量方法、重要意义、解决问题、提高效率。
1. 引言1.1 二面角的概念二面角是立体几何中一个重要的概念,指的是由两个相邻平面夹角所确定的角。
在几何中,我们通常将两个相邻平面的交线称为边线,而边线延伸至无穷远处,形成一个平面角。
这个平面角就是二面角。
二面角可以用来描述空间中两个平面的夹角大小和方向,是立体几何中的基本概念之一。
二面角的大小可以通过其所包含的两个平面的夹角来确定,通常用度数来表示。
二面角的方向则取决于两个相邻平面的相对位置。
在立体几何中,我们经常需要根据二面角的平面角来确定点、线、面等的位置关系,从而推导出更复杂的结论。
掌握二面角的概念和特性对于解决立体几何中的问题至关重要。
通过深入理解二面角的平面角的定位,我们可以更好地理解空间中的几何关系,提高解题效率,解决更为复杂的几何问题。
1.2 平面角的定义平面角是指在几何中由两条射线或直线段围成的角,这两条射线或直线段共同形成了一个平面。
平面角的大小可以通过角度来度量,常用的单位包括度、弧度等。
在平面几何中,平面角的概念是非常基础和重要的,它帮助我们描述和理解不同几何对象之间的位置关系和相互作用。
平面角的定义可以用于描述各种几何形状之间的相对位置关系,比如直线和直线、直线和平面、平面和平面等。
平面角的大小取决于形成该角的两条射线或直线段之间的夹角大小,这个夹角可以通过工具如量角器或通过数学方法进行测量和计算。
二面角的平面角的求法知识点拨1、二面角的定义以一条直线出发的两个半平面所成的图形叫做二面角,记作:二面角α—l —β。
二面角出现的状态形式有:竖立式、横卧式、倒向式2、二面角的平面角的定义以二面角的顶点任意一点为端点,在两个面内分别作垂直于边的两条射线,这两条射线所成的角叫做二面角的平面角。
二面角的平面角的定义要注意三个重要的词组:“棱上”、“面上”、“垂直”, 事实上, 二面角的平面角具有三个要素:(1)过棱上任意一点;(2)分别在两个面内引射线;(3)射线垂直于棱。
其中(1)(2)决定了平面角的两边是在同一平面内。
所以才有“平面角”之称, (3)是决定了平面角的数值的唯一性。
由二面角的平面角的定义可知: 二面角的棱垂直于二面角的平面角所在平面。
平面角是直角的二面角叫做直二面角.3、二面角大小求法的要领二面角的大小,可以用它的平面角来度量,二面角的平面角是几度,就说这个二面角是几度.( 也可转化为求三角形内角问题)4、求二面角大小的基本方法我们总结一下作二面角平面角的几种基本方法. (1)定义法;(2)垂面法;(3)三垂线法;(4)面积法cos θ=S 射影多边形/S 多边形(射影面积公式)。
(1)如何利用定义作二面角的平面角呢?在二面角的棱a 上任意取一点O 为端点,在面α,β内分别引垂直于棱a 的两条射线OA ,OB ,则∠AOB 为该二面角的平面角.(2)如何利用三垂线定理(或其逆定理)作二面角的平面角呢?在二面角α-a-β的面α上任取一点A ,过A 分别作棱a 和另一面β的垂线AO 和AB(O ,B 分别是垂足),连BO ;或者过A 作面β的垂线AB ,又过垂足B 引棱a 的垂线BO ,连AO ;则∠AOB 为该二面角的平面角.(3)如何用作垂面的办法作二面角的平面角呢?过二面角的棱a上任一点O,作平面γ与该棱垂直(作棱的垂面),平面γ与α,β分别交于OA,OB,则可用∠AOB来度量二面角α-a-β的大小.(4)射影面积公式用此方法可避免寻找二面角的平面角的繁琐步骤。