二面角的平面角的五种基本图形及作法

二面角的平面角及求法1、二面角的定义:从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱，这两个半平面叫做二面角的面.棱为AB、面分别为a、0的二面角记作二面角a-45-0.有时为了方便，也可在a、P内（棱以外的半平面部分）分别取点尸、0,将这个二面角记作夕-AB-Q.如果棱记作/,那么这个二面角记作二面角a-/-0或尸2、二面角的平面角在二面角a-/-0的棱/上任取一点0,以点0为垂足，在半平面a和0内分别作垂直于棱/的射线。

4和08,则射线04和06构成的N4O6叫做二面角的平面角.二面角的大小可以用它的平面角来度量，二面角的平面角是多少度，就说这个二面角是多少度.平面角是直角的二面角叫做直二面角.二面角的平面角NZ06的大小与点。

的位置无关，也就是说，我们可以根据需要来选择棱/上的点0.3、二面角的平面角求法：（1）定义；（2）三垂线定理及其逆定理；①定理内容：在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么，它就和这条斜线垂直.②三垂线定理（逆定理）法：由二面角的一个面上的斜线（或它的射影）与二面角的棱垂直，推得它位于二面角的另一的面上的射影（或斜线）也与二面角的棱垂直，从而确定二面角的平面角.（3）找（作）公垂面法：由二面角的平面角的定义可知两个面的公垂面与棱垂直，因此公垂面与两个面的交线所成的角，就是二面角的平面角.；（4）平移或延长（展）线（面）法；（5）射影公式;（6）化归为分别垂直于二面角的两个面的两条直线所成的角；(7)向量法：用空间向量求平面间夹角的方法：设平面a和0的法向量分别为:和若两个平面的夹角为仇则(1)当O〈Vu，v>^—，e=Vu，v>，此时cose=cosVu，v>=-7-^—.2 lullvl―♦―♦—♦1]■V (2)当——<<u，V>W TT时，0=cos(n-Vu，v>)=-cos<u，v>=-=———2 lullvl。

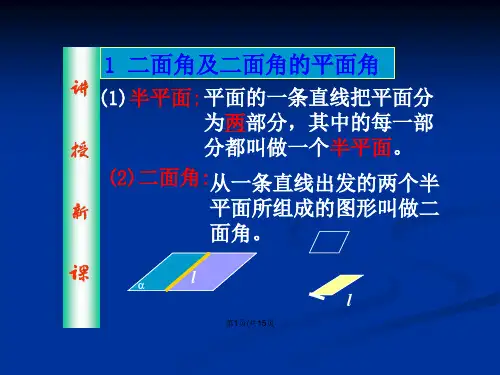
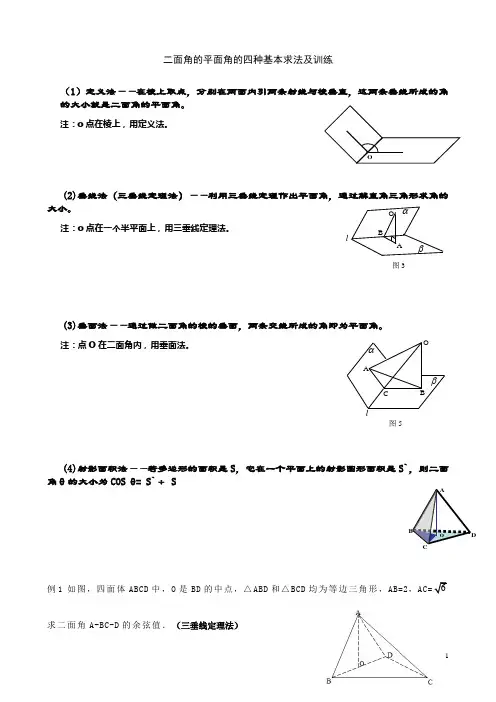
二面角的平面角的四种基本求法及训练（1）定义法——在棱上取点，分别在两面内引两条射线与棱垂直，这两条垂线所成的角的大小就是二面角的平面角。

注：o 点在棱上，用定义法。

(2)垂线法（三垂线定理法）——利用三垂线定理作出平面角，通过解直角三角形求角的大小。

注：o 点在一个半平面上，用三垂线定理法。

(3)垂面法——通过做二面角的棱的垂面，两条交线所成的角即为平面角。

注：点O 在二面角内，用垂面法。

(4)射影面积法——若多边形的面积是S ，它在一个平面上的射影图形面积是S`，则二面角θ的大小为COS θ= S`÷ S例求二面角A-BC-D 的余弦值．（三垂线定理法）A 图3αβO BlO图5βαlCBAD例2 在60°二面角M －a －N 内有一点P ，P 到平面M 、平面N 的距离分别为1和2，求点P 到直线a 的距离。

（垂面法）例3 如图在三棱锥 S-ABC 中，SA ⊥底面ABC ，AB ⊥BC ，DE 垂直平分SC ，且分别交 AC 、SC 于D 、E ，又SA =AB ，BS =BC ， 求以BD 为棱，BDE 与BDC 为面的二面角的度数。

（定义法）例4如图△ABC 与△BCD 所在平面垂直，且AB =BC =BD ，∠ABC =∠DBC =120，求二面角 A-BD-C 的余弦值。

（补棱法和射影面积法）AC例5.在四棱锥P-ABCD 中，ABCD 为正方形，PA ⊥平面ABCD ，PA ＝AB ＝a ，求平面PBA 与平面PDC 所成二面角的大小。

（补棱法和射影面积法）练习题1．如图，二面角α-l-β的大小是60°，线段AB ⊂α．B ∈l ，AB 与l 所成的角为30°．则AB 与平面β所成的角的正弦值是2.山坡与水平面成30︒角，坡面上有一条与坡角水平线成30︒角的直线小路，某人沿小路上坡走了一段路程后升高了100米，则此人行走的路程为 3．在一个二面角的一个面内有一个点，它到棱的距离等于到另一个面的距离的2倍，则二面角的度数为 。

立体几何-二面角求解五法一、定义法：从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面，在棱上取点，分别在两面内引两条射线与棱垂直，这两条垂线所成的角的大小就是二面角的平面角。

本定义为解题提供了添辅助线的一种规律。

如例1中从二面角S —AM —B 中半平面ABM 上的一已知点（B ）向棱AM 作垂线，得垂足（F ）；在另一半平面ASM 内过该垂足（F ）作棱AM 的垂线（如GF ），这两条垂线（BF 、GF ）便形成该二面角的一个平面角，再在该平面角内建立一个可解三角形，然后借助直角三角函数、正弦定理与余弦定理解题。

例1如图，四棱锥S ABCD -中，底面ABCD 为矩形，SD ⊥底面ABCD ，2AD =2DC SD ==，点M 在侧棱SC 上，ABM ∠=60°（I ）证明：M 在侧棱SC 的中点（II ）求二面角S AM B --的大小。

解证（I ）略 （II ）：利用二面角的定义。

在等边三角形ABM 中过点B 作BF AM ⊥交AM 于点F ，则点F 为AM 的中点，过F 点在平面ASM 内作GF AM ⊥，GF 交AS 于G ，连结AC ，∵△ADC ≌△ADS ，∴AS-AC ，且M 是SC 的中点， ∴AM ⊥SC ， GF ⊥AM ，∴GF ∥AS ，又∵F 为AM 的中点， ∴GF 是△AMS 的中位线，点G 是AS 的中点。

则GFB ∠即为所求二面角. ∵2=SM ，则22=GF ，又∵6==AC SA ，∴2=AM ∵2==AB AM ，060=∠ABM ∴△ABM 是等边三角形，∴3=BF在△GAB 中，26=AG ，2=AB ，090=∠GAB ， ∴211423=+=BG FGFG366232222113212cos 222-=-=⨯⨯-+=⋅-+=∠FB GF BG FB GF BFG ∴二面角S AM B --的大小为)36arccos(-练习1如图，已知四棱锥P -ABCD ，底面ABCD 为菱形，P A ⊥平面ABCD ，60ABC ∠=︒,E ，F 分别是BC , PC 的中点. （Ⅰ）证明：AE ⊥PD ;（Ⅱ）若H 为PD 上的动点，EH 与平面P AD 所成最大角的正切值为6，求二面角E —AF —C 的余弦值. 分析：第1题容易发现，可通过证AE ⊥AD 后推出AE ⊥平面APD ，使命题获证，而第2题，则首先必须在找到最大角正切值有关的线段计算出各线段的长度之后，考虑到运用在二面角的棱AF 上找到可计算二面角的平面角的顶点S ，和两边SE 与SC ，进而计算二面角的余弦值。