1.2.3单位圆中的三角函数线
- 格式:ppt
- 大小:983.00 KB
- 文档页数:27

高考数学知识点:三角函数线(正弦线、余弦线、正切线)高考数学知识点:三角函数线(正弦线、余弦线、正切线)三角函数线的定义:设任意角α的顶点在原点O,始边与x轴的正半轴重合,终边与单位圆相交于点P(x,y),过P点作x轴的垂线,垂足为M,过点A(1,0)作单位圆的切线,高二,设它与角α的终边或其反向延长线相交于点T,则有向线段MP、OM,AT分别叫做角α的正弦线,余弦线,正切线,即:sinα=MP,cosα=OM,ta nα=AT,如下图:注:线段长度表示三角函数值大小,线段方向表示三角函数值正负。
关于三角函数线,要注意以下几点:(1)正弦线、余弦线、正切线都是有向线段,利用它们的数量来表示三角函数值,是数形结合的典型体现。
三角函数线表示三角的函数值的符号规定如下:正弦线MP、正切线AT方向与y轴平行,向上为正,向下为负;余弦线OM在x 轴上,向右为正,向左为负。
(2)作三角函数线时,所用字母一般都是固定的,书写顺序也不能颠倒。
特别要注意正切线必在过A(1,0)的单位圆的切线上(其中二、三象限角需作终边的反向延长线)。
(3)对于终边在坐标轴上的角,有时三角函数线退化为一个点,有时又为整个半径。
当角α的终边在y轴上时,角α的正切线不存在。
(4)当时,正弦线、余弦线、正切线与角α并不是一一对应的。
一般地,每一个确定的MP、OM、AT都对应两个α的值。
诱导公式:公式一公式二公式三公式四公式五公式六规律:奇变偶不变,符号看象限。
即形如(2k+1)90°±α,则函数名称变为余名函数,正弦变余弦,余弦变正弦,正切变余切,余切变正切。
形如2k×90°±α,则函数名称不变。
诱导公式口诀“奇变偶不变,符号看象限”意义:的三角函数值.(1)当k为偶数时,等于α的同名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号;(2)当k为奇数时,等于α的异名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号。

利用三角函数线比较函数值大小课后作业:一、选择题1.对三角函数线,下列说法正确的是( ) A .对任何角都能作出正弦线、余弦线和正切线 B .有的角正弦线、余弦线和正切线都不存在C .任何角的正弦线、正切线总是存在,但余弦线不一定存在D .任何角的正弦线、余弦线总是存在,但是正切线不一定存在2.角α(0<α<2π)的正弦线与余弦线长度相等且符号相同,那么α的值为( )A.π4或34πB.5π4或74πC.π4或54πD.π4或74π 3.若角α的正切线位于第一象限,则角α属于( )A .第一象限B .第一、二象限C .第三象限D .第一、三象限 4.下列命题中为真命题的是( )A .三角形的内角必是第一象限的角或第二象限的角B .角α的终边在x 轴上时,角α的正弦线、正切线都变成一个点C .终边在第二象限的角是钝角D .终边相同的角必然相等5.若-3π4<α<-π2,则sin α、cos α、tan α的大小关系是( )A .sin α<tan α<cos αB .tan α<sin α<cos αC .cos α<sin α<tan αD .sin α<cos α<tan α6.在[0,2π]上满足sin x ≥12的x 的取值范围是( )A .[0,π6]B .[π6,5π6]C .[π6,2π3]D .[5π6,π]7.在(0,2π)内使cos x >sin x >tan x 成立的x 的取值范围是( )A .(π4,3π4)B .(5π4,3π2)C .(3π2,2π)D .[3π2,7π4]8.如果cos α=cos β,则角α与β的终边除可能重合外,还有可能( )A .关于x 轴对称B .关于y 轴对称C .关于直线y =x 对称D .关于原点对称9.设a =sin 5π7,b =cos 2π7,c =tan 2π7,则( )A .a <b <cB .a <c <bC .b <c <aD .b <a <c 10.函数x x y cos sin -+=的定义域是( )A .))12(,2(ππ+k k ,Z k ∈B .])12(,22[πππ++k k ,Z k ∈C .])1(,2[πππ++k k , Z k ∈ D .[2k π,(2k+1)π],Z k ∈二、填空题11.不等式cos α≤12的解集为________.12.若θ∈(3π4,π),则下列各式错误的是________.①sin θ+cos θ<0;②sin θ-cos θ>0;③|sin θ|<|cos θ|;④sin θ+cos θ>0.13.若0≤sin θ<32,则θ的取值范围是________.14.函数y =sin x +cos x -12的定义域是____________.。


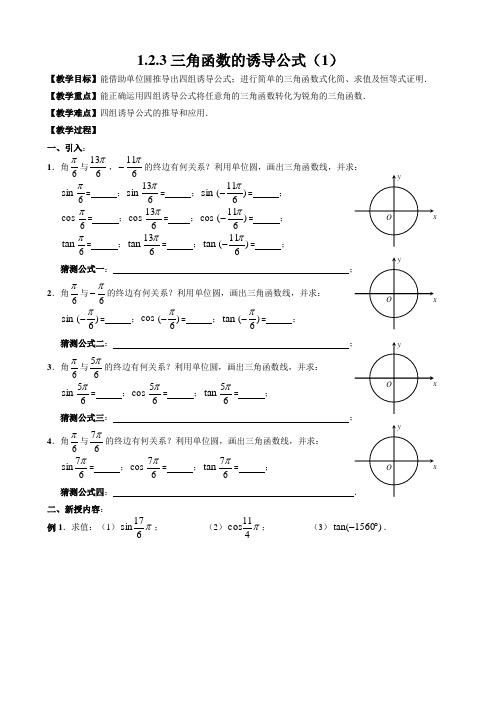
1.2.3三角函数的诱导公式(1)【教学目标】能借助单位圆推导出四组诱导公式;进行简单的三角函数式化简、求值及恒等式证明.【教学重点】能正确运用四组诱导公式将任意角的三角函数转化为锐角的三角函数. 【教学难点】四组诱导公式的推导和应用. 【教学过程】 一、引入: 1.角6π与613π,611π-的终边有何关系?利用单位圆,画出三角函数线,并求:sin 6π= ;sin 613π= ;sin )611(π-= ; cos 6π= ;cos 613π= ;cos )611(π-= ;tan 6π= ;tan 613π= ;tan )611(π-= ; 猜测公式一:;2.角6π与6π-的终边有何关系?利用单位圆,画出三角函数线,并求:sin )6(π-= ;cos )6(π-= ;tan )6(π-= ;猜测公式二: ;3.角6π与65π的终边有何关系?利用单位圆,画出三角函数线,并求:sin 65π= ;cos 65π= ;tan 65π= ; 猜测公式三: ;4.角6π67sin π二、新授内容: 例1.求值:(1)π617sin ; (2)π411cos; (3))1560tan(︒-.例2.判断下列函数的奇偶性:(1)x x f cos 1)(-=; (2)x x x g sin )(-=; (3)x x x h tan )(2+=.例3.已知)6cos(απ-=33,求)65cos(απ+-)6(sin 2πα-的值.【变式拓展】(1)若cos(α-π)=-23,求sin (α-2π)+sin (-α-3π)cos (α-3π)cos (π-α)-cos (-π-α)cos (α-4π)的值.(2)设()f θ=)cos()7(cos 221)cos(2)(sin cos 2223θθππθπθθ-++++---+-,求()3f π的值.三、课堂反馈:1.计算下列各三角函数值:sin()4π-= ; c o s (60)-= ; 7tan 6π= ; sin 225= ;3sin()4π-= ; 0tan1020= ; sin150= ; sin(750)-= .2.cos(π-α)= —21, 02πα-<<,sin(πα+)= .3.若3sin()65πα-=,则=+)65sin(απ. 4.判断下列函数的奇偶性:(1)()|sin |f x x =; (2)()sin cos f x x x =.四、课后作业: 姓名:___________ 成绩:___________ 1.化简:sin()cos()sin(2)cos()=πααπαπα+-+-- .2.已知()()()()29cos sin 4cos sin 3=+---++απαααπ,则αtan = . 3.已知sin(4π+α)=23,则sin(34π—α)= .4.已知53)cos(-=+απ,且α为第四象限角,则)2sin(απ+-等于 . 5.)(sin 2απ+-⋅+)cos(απ1)cos(+-α的值是 . 6.若sin(π-α)=log 8 14,且α∈⎝⎛⎭⎫-π2,0,则cos(π+α)的值为 . 7.已知cos(π6+θ)=33,则cos(5π6-θ)= .8.求下列三角函数值:(1)sin 960;(2)43cos()6π-; (3)π3331tan .9.(1)化简:sin cos()tan()απαπα+--;(2)化简:)(cos 2)sin()2sin(12ααπαπ--++-+.10.判断下列函数的奇偶性:(1)()3cos 1f x x =-; (2)3()sin f x x x =; (3)()cos(sin )f x x =.11.已知sin )6(π+x =41,求)65(cos )67sin(2x x -++ππ的值.12.已知 3)tan(=+απ,求)2sin()cos(4)sin(3)cos(2a a a a -+-+--πππ的值.。

高考数学知识点:三角函数线(正弦线、余弦线、正切线)_知识点总结高考数学知识点:三角函数线(正弦线、余弦线、正切线)三角函数线的定义:设任意角α的顶点在原点O,始边与x轴的正半轴重合,终边与单位圆相交于点P(x,y),过P点作x轴的垂线,垂足为M,过点A(1,0)作单位圆的切线,高二,设它与角α的终边或其反向延长线相交于点T,则有向线段MP、OM,AT分别叫做角α的正弦线,余弦线,正切线,即:sinα=MP,cosα=OM,tanα=AT,如下图:注:线段长度表示三角函数值大小,线段方向表示三角函数值正负。
关于三角函数线,要注意以下几点:(1)正弦线、余弦线、正切线都是有向线段,利用它们的数量来表示三角函数值,是数形结合的典型体现。
三角函数线表示三角的函数值的符号规定如下:正弦线MP、正切线AT 方向与y轴平行,向上为正,向下为负;余弦线OM在x轴上,向右为正,向左为负。
(2)作三角函数线时,所用字母一般都是固定的,书写顺序也不能颠倒。
特别要注意正切线必在过A(1,0)的单位圆的切线上(其中二、三象限角需作终边的反向延长线)。
(3)对于终边在坐标轴上的角,有时三角函数线退化为一个点,有时又为整个半径。
当角α的终边在y轴上时,角α的正切线不存在。
(4)当时,正弦线、余弦线、正切线与角α并不是一一对应的。
一般地,每一个确定的MP、OM、AT都对应两个α的值。
诱导公式:公式一公式二公式三公式四公式五公式六规律:奇变偶不变,符号看象限。
即形如(2k+1)90°±α,则函数名称变为余名函数,正弦变余弦,余弦变正弦,正切变余切,余切变正切。
形如2k×90°±α,则函数名称不变。
诱导公式口诀“奇变偶不变,符号看象限”意义:的三角函数值.(1)当k为偶数时,等于α的同名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号;(2)当k为奇数时,等于α的异名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号。
三角函数单位圆的定义§1.2.1 任意角的三角函数第一课时任意角的三角函数的定义三角函数的定义域和函数值【学习目标、细解考纲】1、借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义;2、从任意角三角函数的定义认识其定义域、函数值的符号。
【知识梳理、双基再现】1、在直角坐标系中,叫做单位圆。
2、设α是一个任意角, 它的终边与单位圆交于点P(x,y),那么: ⑴ 叫做α的正弦, 记作 ,即. ⑵ 叫做α的余弦, 记作 ,即. ⑶ 叫做α的正切, 记作 ,即 .当α= 时, α的终边在y 轴上, 这时点P 的横坐标等于 ,所以无意义. 除此之外, 对于确定的角α, 上面三个值都是 . 所以, 正弦、余弦、正切都是以为自变量, 以为函数值的函数, 我们将它们统称为 . 由于与之间可以建立一一对应关系, 三角函数可以看成是自变量为的函数.3、根据任意角的三角函数定义,先将正弦余弦正切函数在弧度制下的定义域填入下表,再将这三种函数的值在各象限的符号填入括号。
y =sin α y = cos αy =tan α【小试身手、轻松过关】4、已知角α的终边过点P (-1,2),cos α的值为() A .-5 B 5 C .25 D .25、α是第四象限角,则下列数值中一定是正值的是() A .sin α B .cosαC .tan α D .1tan α6、已知角α的终边过点P (4a , -3a )(aA .25B 25 C .0 D .与α的取值有关7、α是第二象限角,P (x , 5 )为其终边上一点,且cos α= 24x ,则sin α的值为(A .4 B .24 C .4 D .-4【基础训练、锋芒初显】8、函数y =x +-cos x 的定义域是()A .(2k π, (2k +1) π) ,k ∈ZB .[2k π+π2, (2k +1) π],k ∈Z)C .[k π+π2, (k +1) π],k ∈ZD .[2kπ,(2k+1)π],k ∈Z()9、若θ是第三象限角,且cosθ2θ是 2A .第一象限角B .第二象限角C .第三象限角 10、已知点P (tan α, cos α)在第三象限,则角α在A .第一象限B .第二象限C .第三象限D .第四象限角() D .第四象限11、已知sin αtan α≥0,则α的取值集合为 12、角α的终边上有一点P (m ,5),且cos α=m, (m ≠0) ,则sin α+cosα=______. 1313、已知角θ的终边在直线y =x 上,则sin θtan θ 314、设θ∈(0,2π),点P (sin θ,cos2θ)在第三象限,则角θ的范围是 15、函数y =A .{1}sin x |cos x |tan x++的值域是|sin x |cos x |tan x |B .{1,3}()C .{-1}D .{-1,3}【举一反三、能力拓展】17、(1) 已知角α的终边经过点P(4,-3) ,求2sin α+cosα的值;【名师小结、感悟反思】当角α的终边上点的坐标以参数形式给出时, 要根据问题的实际及解题的需要对参数进行分类讨论.§1.2.1 任意角的三角函数第二课时诱导公式一三角函数线【学习目标、细解考纲】灵活利用利用公式一;掌握用单位圆中的线段表示三角函数值,从而使学生对三角函数的定义域、值域有更深的理解。