下载文档原格式
§6.3* 平面运动刚体上点的加速度由于平面运动可以看成是随同基点的牵连平移与绕基点的相对转动的合成运动，于是图形上任一点的加速度可以由加速度合成定理求出。
设已知某瞬时图形内A 点的加速度a A ，图形的角速度为ω，角加速度为α，如图6-13所示。
以A 点为基点，分析图形上任意一点B 的加速度a B 。
因为牵连运动为动坐标系随同基点的平移，故牵连加速度a e =a A 。
相对运动是点B 绕基点A 的转动，故相对加速度a r =a BA ，其中a BA 是点B 绕基点A 的转动加速度。
由式 (5.3.7)可得图6-13 加速度分析的基点法 α (6.3.1) BA A B αα+=由于B 点绕基点A 转动的加速度包括切向加速度和法向加速度a ，故式(6.3.1)可写为t BA a n BAa (6.3.2) n t BA BA A B a a a ++=即平面图形上任意一点的加速度，等于基点的加速度与该点绕基点转动的切向加速度和法向加速度的矢量和。
当基点A 和所求点B 均作曲线运动时，它们的加速度也应分解为切向加速度和法向加速度的矢量和，因此，式(6.3.2)可表示为(6.3.3)n t n t n t BA BA A A B B a a a a a a +++=+在式(6.3.3)中，相对切向加速度与点A 和B 连线方向垂直，相对法向加速度沿点A 和B连线方向从B 指向A ；仅当点A 和B 的运动轨迹已知时，才可以确定点A 和B 的切向加速度a 和及法向加速度和a 。
t BA a n BA a t A t B a n A a n B 在应用式(6.3.2)或(6.3.3)计算平面图形上各点的加速度时，只能求解矢量表达式中的两个要素。
因此在解题时，要注意分析所求问题是否可解。
当问题可解时，将式(6.3.2)或(6.3.3)在平面直角坐标系上投影，即可由两个代数方程联立求得所需的未知量。
例6.3-2：半径为R 的车轮沿直线滚动，某瞬时轮心O 点的速度为v O ，加速度为a O ，如图a 所示。
理论力学中的刚体运动与角动量的计算理论力学是研究物体运动的基本规律的科学。
刚体是理论力学中的重要概念之一，它指的是一个具有有限尺寸的物体，在运动中不发生形变的物体。
刚体运动及其角动量计算是理论力学中的重要内容，本文将从刚体运动的基本概念入手，介绍角动量的定义与计算方法。
1. 刚体运动的基本概念刚体运动是指刚体在空间中的运动。
刚体的转动可以分为平面运动和空间运动两种情况。
平面刚体运动是指刚体的所有点都在一个平面内运动，而空间刚体运动是指刚体的某些点在不同的平面内运动。
刚体运动可以分为平动和转动两个部分，平动是指刚体整体平移而不转动，转动则是指刚体绕某个轴线旋转。
2. 角动量的定义角动量是刚体运动中的重要物理量，它描述了刚体绕某个轴线旋转时的转动效果。
角动量的定义可以通过刚体质点系的线性动量来表示。
对于一个质点系来说，其角动量L可以表示为L=r×p，其中r为质点相对于参考点的位矢，p为质点的线性动量。
当质点系内的所有质点都绕同一个轴线旋转时，可以将整个质点系的角动量定义为各个质点的角动量之和。
3. 角动量的计算方法刚体绕固定轴线旋转时，可以利用角动量守恒定律来计算角动量的变化。
角动量守恒定律指出，当刚体受到外力时，其总角动量守恒，即刚体围绕固定轴线的角动量不变。
根据角动量守恒定律，可以通过刚体的质量分布和旋转速度来计算刚体的角动量。
当刚体质量分布均匀时，计算刚体的角动量较为简单。
可以使用以下公式来计算：L = I * ω其中L为角动量，I为刚体对于旋转轴的转动惯量，ω为刚体的角速度。
转动惯量I是描述刚体旋转惯性的物理量，其大小与刚体的质量分布以及旋转轴的位置有关。
当刚体质量分布不均匀时，计算刚体的角动量可以采用积分的方法进行计算。
通过将刚体分割成无限小的质量元，可以求得每个质量元的角动量，并将其累加得到整个刚体的角动量。
4. 刚体运动与角动量的应用刚体运动与角动量计算在物理学和工程学中有着广泛的应用。
理论力学课后习题答案-第6章--刚体的平面运动分析第6章 刚体的平面运动分析6－1 图示半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动，当运动开始时，角速度0ω= 0，转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解：ϕc o s )(r R x A += （1） ϕsin )(r R y A+= （2）α为常数，当t = 0时，0ω=0ϕ= 0 221t αϕ= （3） 起始位置，P 与P 0重合，即起始位置AP 水平，记θ=∠OAP ，则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚，故有⋂⋂=CP CP 0，即 θϕr R =ϕθr R =， ϕϕrrR A+=（4） 将（3）代入（1）、（2）、（4）得动齿轮以A 为基点的平面运动方程为：⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R tr R y t r R x A A A αϕαα6－2 杆AB 斜靠于高为h 的台阶角C 处，一端A 以匀速v 0沿水平向右运动，如图所示。
试以杆与铅垂线的夹角θ 表示杆的角速度。
解：杆AB 作平面运动，点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ，点P 即为杆AB 的速度瞬心。
则角速度杆AB习题6-1图A BCv 0hθ 习题6－2图 P ωAv CA BC v oh θ 习题6－2解图为6－3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时，轮A 与垫滚B 的角速度A ω与B ω有什么关系？设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解：Rv R v A A ==ωRv R v B B 22==ωB A ωω2=6－4 直径为360mm 的滚子在水平面上作纯滚动，杆BC 一端与滚子铰接，另一端与滑块C 铰接。
设杆BC 在水平位置时，滚子的角速度ω＝12 rad/s ，θ＝30︒，ϕ＝60︒，BC ＝270mm 。
基础部分——运动学第5 章点的一般运动与刚体的基本运动一、运动学的研究对象及任务点刚体zz几何性质z合成分解例1例2例3例4例5例6二、学习运动学的目的三、运动学的分析方法矢量工具数值求解工具四、具体内容第5章点的一般运动与刚体的基本运动点的运动的矢量法点的运动的直角坐标法点的运动的弧坐标法一、运动方程二、轨迹三、点的速度O)(t r )(t t Δ+r vMM ′位矢四、点的加速度点的运动的矢量法一、运动方程点的运动的直角坐标法O rMxy z)(zy,x,xyz二、轨迹方程三、点的速度四、点的加速度AB点的运动的弧坐标法运动轨迹原点O 一、运动方程sMO)(−)(+正方向弧坐标s二、自然轴系主法线n 切线τ，指副法线b思考：共同点不同点)(t r M O三、点的速度⋅lim ⋅st s d d d d r⋅τ⋅=v tsv d d =)(t t Δ+r vM ′sΔO)(−)(+r Δτ四、点的加速度速度大小随时间的变化率方向ττa 22t d d d d tst v ==22t d d d d tst v a ==z切向tas t ΔΔ⋅→Δτ0lim⋅速度方向随时间的变化率z法向n a sΔΔτs ΔΔϕsd d ϕ→方向？n2n2taa +全t 讨论：加速减速[例5-1]纯滚动解：（1）运动方程运动方程=x =y （2）速度22yxv v +t ωcos 22−（3）切向、法向加速度思考：如何求速度投影加速度投影全加速度22a a yx +法向加速度2t2aa −曲率半径（4）运动方程（弧坐标）如何取弧坐标的原点？讨论：Array纯滚动速度为零加速度不为零5-4-1 平行移动（平移）任一直线z形状相同z速度相同z加速度相同5-4-2 定轴转动=矢量表示:=右手规则滑动矢量αωαkz线速度v（弧坐标法）Rv ω=Rna ta αta 方向?z加速度aRa α=t Ra 2n ω=2n2t aa +42ωα+t a α思考：过轴的任一条直线上θαθrωv ×=ααt a rαa ×=t na vωa ×=nr ωr×=td d αααx ′y ′z ′1O i ′j ′k ′rωv ×=[例5-2]解：r ω=+d d r tω−=avtr R +=22ππ[思考题]j i i k ⎜+′⎟⎜′⋅+′⎟′⋅提示：5-5-1 注意区别几组公式5-5-2 描述点的运动的其它方法点的一般运动与刚体基本运动点的一般运动刚体基本运动矢量法直角坐标法弧坐标法其它方法平移定轴转动5-5-3 本章知识结构框图补充：轮系的传动比一、齿轮传动z速度z 切向加速度外啮合内啮合=两齿轮之传动比：21=1 2112R R i ==ωω2112ωω=i 22211±=±=±=正号內啮合负号外啮合11±=外啮合转向推广：二、带轮（链轮）传动二、带轮（链轮）传动z z 皮带与带轮间无相对滑动。
理论力学运动学知识点总结第一篇：理论力学运动学知识点总结运动学重要知识点一、刚体的简单运动知识点总结1.刚体运动的最简单形式为平行移动和绕定轴转动。
2.刚体平行移动。
·刚体内任一直线段在运动过程中，始终与它的最初位置平行，此种运动称为刚体平行移动，或平移。
·刚体作平移时，刚体内各点的轨迹形状完全相同，各点的轨迹可能是直线，也可能是曲线。
·刚体作平移时，在同一瞬时刚体内各点的速度和加速度大小、方向都相同。
3.刚体绕定轴转动。
• 刚体运动时，其中有两点保持不动，此运动称为刚体绕定轴转动，或转动。
• 刚体的转动方程φ=f(t)表示刚体的位置随时间的变化规律。
• 角速度ω表示刚体转动快慢程度和转向，是代数量，以用矢量表示。
，当α与ω。
角速度也可• 角加速度表示角速度对时间的变化率，是代数量，同号时，刚体作匀加速转动；当α 与ω异号时，刚体作匀减速转动。
角加速度也可以用矢量表示。
• 绕定轴转动刚体上点的速度、加速度与角速度、角加速度的关系：。
速度、加速度的代数值为。
• 传动比。
一、点的运动合成知识点总结1.点的绝对运动为点的牵连运动和相对运动的合成结果。
• 绝对运动：动点相对于定参考系的运动；• 相对运动：动点相对于动参考系的运动；• 牵连运动：动参考系相对于定参考系的运动。
2.点的速度合成定理。
• 绝对速度：动点相对于定参考系运动的速度；• 相对速度：动点相对于动参考系运动的速度；• 牵连速度：动参考系上与动点相重合的那一点相对于定参考系运动的速度。
3.点的加速度合成定理。
• 绝对加速度：动点相对于定参考系运动的加速度；• 相对加速度：动点相对于动参考系运动的加速度；• 牵连加速度：动参考系上与动点相重合的那一点相对于定参考系运动的加速度；• 科氏加速度：牵连运动为转动时，牵连运动和相对运动相互影响而出现的一项附加的加速度。
• 当动参考系作平移或 = 0，或与平行时，= 0。
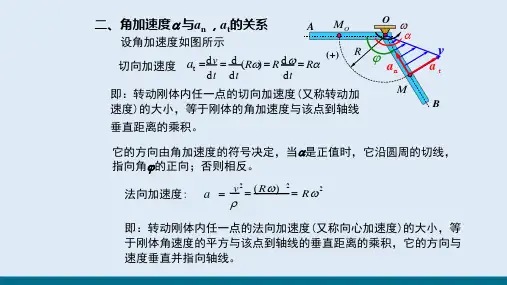
理论力学中的刚体运动与力学参数计算理论力学是力学的基础理论之一，研究物体在力的作用下的运动规律以及相关力学参数的计算。
刚体运动是理论力学研究的重要内容之一，刚体是指在外力作用下，物体内部各部分的相对位置保持不变的物体。
本文将针对理论力学中的刚体运动进行探讨，并介绍相关的力学参数计算方法。
一、刚体运动的类型刚体运动主要包括平动和转动两种类型。
平动是指刚体的质心沿直线轨迹运动，质心速度相等。
而转动是指刚体围绕某一轴旋转，各点角速度相等，且轴上任意两点连线垂直于轴。
根据刚体的运动类型，可以采用不同的方法进行力学参数的计算。
二、平动刚体运动的力学参数计算1. 速度：平动刚体的速度由质心速度来表示，质心速度的计算公式为v = Δx/Δt，其中Δx为质心位置变化的距离，Δt为质心位置变化所经过的时间。
2. 加速度：平动刚体的加速度由质心加速度来表示，质心加速度的计算公式为a = Δv/Δt，其中Δv为质心速度变化的差值，Δt为质心速度变化所经过的时间。
3. 质量：平动刚体的质量常用m来表示，可以通过测量质心处的物体质量来得到，计算公式为m = F/g，其中F为物体所受合力的大小，g为重力加速度。
三、转动刚体运动的力学参数计算1. 角速度：转动刚体的角速度由角位移与时间的比值来表示，角速度的计算公式为ω = Δθ/Δt，其中Δθ为角位移的变化值，Δt为变化所经过的时间。
2. 角加速度：转动刚体的角加速度由角速度变化的差值与时间变化量的比值来表示，角加速度的计算公式为α = Δω/Δt，其中Δω为角速度的变化差值，Δt为角速度变化所经过的时间。
3. 转动惯量：转动刚体的转动惯量常用I来表示，转动惯量决定了物体在旋转运动中的惯性大小。
转动惯量的计算公式为I = ΣmiRi^2，其中mi为物体质点的质量，Ri为质点到转轴的距离。
四、力学参数计算实例以平动刚体为例，假设一个质量为m的物体受到一个水平方向的恒定力F作用，求该物体在t时间后的速度v。
