第八章 应力状态和强度理论
- 格式:pdf
- 大小:330.90 KB
- 文档页数:11



第8章 强度理论Chapter 8 Strength Theories8.1 、材料的破坏形式 Types of failure of materials(1)材料破坏的基本形式:Basic forms of failure of materials材料破坏试验研究和工程实践都表明:尽管材料的破坏现象各不相同,但破坏的形式可以归纳为两类:塑性屈服和脆性断裂。
塑性屈服 plastically yield材料出现显著塑性变形,失去正常工作能力。
脆性断裂brittle rupture材料在无明显的变形的情况下突然断裂。
金属材料有2种极限抵抗能力,一种是抵抗脆性断裂的极限能力,例如铸铁拉伸的抗拉强度b σ;另一种是抵抗塑性屈服的极限能力,如低碳钢拉伸时的切应力s τ。
脆性材料对塑性屈服的抵抗能力大于脆性断裂的抵抗能力,塑性材料对脆性断裂的抵抗能力大于对塑性屈服的抵抗能力。
(2)应力状态对材料破坏形式的影响Influence of stress state on the failure form of materials铸铁拉伸时脆性破坏,压缩时塑性破坏。
三向拉伸时脆性破坏,三向压缩时塑性破坏。
8.2、强度理论 Theories of strength(1)强度理论的概念 Concepts of theories of strength关于材料破坏原因的学说称为强度理论。
some assumptions about the cause of the strength failure of materials .(2)常用的强度理论Common used strength theoriesA )最大拉应力理论(第一强度理论)Theory of the maximum tensile stress (the first strength )最大拉应力理论,认为构件的断裂是由最大拉应力引起的。
当最大拉应力达到单向拉伸的强度极限时,构件就破坏了,破坏判据为:u σσ=1This theory considers the main cause of rupture to be the maximum tensile stress. The member will rupture as the maximum tensile stress reaches the strength limit in axial tension. Criterion of rupture: u σσ=1最大拉应力理论适用于脆性材料。





第十一章应力状态和强度理论【学时】6(其中习题课2)内容:应力状态的概念,单元体,主应力和主平面;应力状态的分类。
二向应力状态下的应力分析——解析法,斜截面上的应力,主应力和主平面的确定。
三向应力状态的举例与(简单)分析,最大正应力。
广义虎克定律;比能,体积改变比能和形状改变比能。
强度理论的概念;最大拉应力理论;最大伸长线应变理论;最大剪应力理论;形状改变比能理论;相当应力;各种强度理论的使用范围。
【基本要求】1.理解应力状态、单元体、主应力和主平面的概念[2]。
2.了解应力状态的分类[3]。
3.掌握二向应力状态下应力分析的解析法[1]。
4.掌握斜截面上的应力,主应力和主平面的确定[1]。
5.掌握广义虎克定律[1]。
6.了解体积改变比能和形状改变比能[3]。
7.理解强度理论的概念[2]。
8.掌握四个常用强度理论[1]。
9.了解各种强度理论的使用范围[3]。
【重点】平面应力状态的解析法,广义虎克定律,四个常用强度理论【难点】应力状态的概念,强度理论的概念。
§11–1 概述 【问题的提出】拉压、 扭转及弯曲等基本变形的强度条件[][]ττσσ≤≤max max对于更复杂的受力状态, 如图中A 截面上的a 点? ①全面研究一点处各截面的应力——应力状态理论的任务。
②材料在复杂应力状态下的破坏规律——强度理论的任务。
§11–2 平面应力状态的应力分析 【问题的提出】铸铁与低碳钢的拉、压、扭试验现象是怎样产生的?低碳钢PP 铸铁拉伸铸铁压缩 铸铁一、应力状态的概念1.一点的应力状态:过一点有无数的截面,这一点的各个截面上应力情况集合。
2.研究方法:取单元体为研究对象①单元体——构件内的点的代表物,是包围被研究点②单元体的性质——a、同一面上,应力均布;b、平行面上,应力相等。
例1画出下列图中的A、B、C点的已知单元体。
zBCx 3.平面应力状态:只在四个侧面上作用由应力。
x二、斜截面上的应力【分析方法】:利用 α 斜截面截取的微元局部的平衡。




断裂失效断裂失效屈服失效屈服失效断口处材料颗粒状断口处材料颗粒状断口处材料片状断口处材料片状材料失效单向应力状态的试验结果单向应力状态的试验结果关于材料破坏规律的假说,一般假设材料不同应力状态下同种失效由同种因素引起的。
关于材料破坏规律的假说,一般假设材料不同应力状态下同种失效由同种因素引起的。
引起失效的因素已知引起失效的因素已知同种失效引起的因素是相同的同种失效引起的因素是相同的建立复杂应力状态下的强度条件建立复杂应力状态下的强度条件强度理论一、最大拉应力理论(第一强度理论)材料发生断裂是最大拉应力引起,即最大拉应力达到某一极限值时材料发生断裂。
材料发生断裂是最大拉应力引起,即最大拉应力达到某一极限值时材料发生断裂。
1.第一强度理论的计算准则单向应力状态max bσσ=最大拉应力最大拉应力b σ=复杂应力状态max u σσ=材料断裂失效材料断裂失效bσ=引起失效的因素max 1σσ=1bσσ=max u σσ=?=1bσσ=[]1σσ≤2.第一强度理论的的应用与局限材料无裂纹脆性断裂失效形式(脆性材料二向或三向受拉状态;最大压应力值不超过最大拉应力值或超过不多)。
材料无裂纹脆性断裂失效形式(脆性材料二向或三向受拉状态;最大压应力值不超过最大拉应力值或超过不多)。
没考虑σ2、σ3 对材料的破坏影响,对无拉应力的应力状态无法应用。
没考虑σ2、σ3 对材料的破坏影响,对无拉应力的应力状态无法应用。
第一强度理论的断裂准则第一强度理论的强度条件二、最大拉应变理论(第二强度理论)材料发生断裂是最大拉应变引起,即最大拉应变达到某一极限值时材料发生断裂。
材料发生断裂是最大拉应变引起,即最大拉应变达到某一极限值时材料发生断裂。
1.第二强度理论的计算准则b max E σε=单向应力状态b σσ=最大拉应变最大拉应变b E σ=材料断裂失效材料断裂失效引起失效的因素max u εε=?=123max ()E σµσσε−+=b u E σε==123b()σµσσσ−+=b max Eσε=单向应力状态b σσ=最大拉应变最大拉应变b E σ=材料断裂失效材料断裂失效引起失效的因素max u εε=?=复杂应力状态材料断裂失效材料断裂失效2.第二强度理论的的应用与局限123b()σµσσσ−+=[]123()σµσσσ−+≤与极少数的脆性材料在某些受力形式下的实验结果吻合。



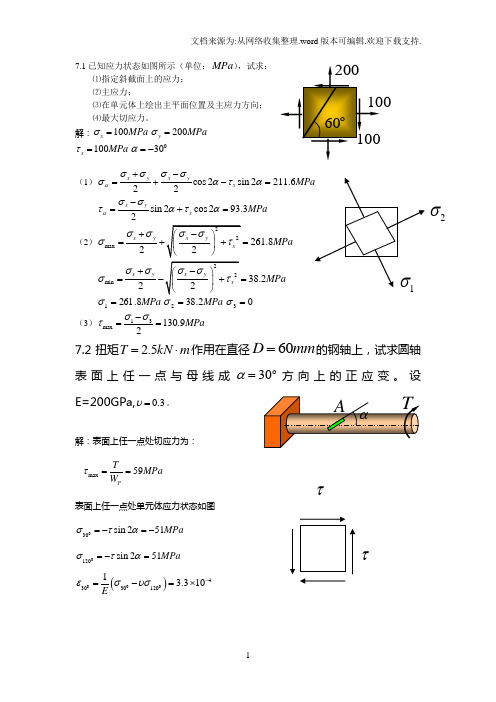
7.1已知应力状态如图所示(单位:MPa ),试求:⑴指定斜截面上的应力; ⑵主应力;⑶在单元体上绘出主平面位置及主应力方向; ⑷最大切应力。
解:100x MPa σ=200y MPa σ=100x MPa τ=030α=-(1)cos 2sin 2211.622x yx yxασσσσσατα+-=+-=sin 2cos 293.32x yx MPa ασστατα-=+=(2)max 261.82x yMPa σσσ+==min 38.22x yMPa σσσ+==MPa 8.2611=σMPa 2.382=σ03=σ(3)13max 130.92MPa σστ-==7.2扭矩m kN T ⋅=5.2作用在直径mm D 60=的钢轴上,试求圆轴表面上任一点与母线成ο30=α方向上的正应变。
设E=200GPa,0.3υ=。
解:表面上任一点处切应力为:max 59PTMPa W τ== 表面上任一点处单元体应力状态如图30sin 251MPa στα=-=-120sin 251MPa στα=-=()004303012013.310Eεσυσ-=-=⨯2σττ7.3用电阻应变仪测得空心钢轴表面某点与母线成ο45方向上的正应变4100.2-⨯=ε,已知转速min /120r ,G=80GPa ,试求轴所传递的功率。
解:表面任一点处应力为max 9550PPP T n W W τ==max 9550P W nP τ∴=纯剪切应力状态下,045斜截面上三个主应力为:1στ=20σ=3στ=-由广义胡克定律 ()11311E E υεσυστ+=-=又()21E G υ=+Q V 2G τε∴= 代入max 9550P W nP τ=,得109.4P KW =7.4图示为一钢质圆杆,直径mm D 20=,已知A 点与水平线成ο60方向上的正应变460101.4-⨯=οε,E=200GPa ,0.3υ=,试求荷载P 。


建 筑 力 学 刘国华 阚小妹主编电子工业出版社第八章应力状态和强度理论【知识目标】●了解平面及空间应力状态的概念●熟悉平面应力状态的分析方法●熟悉空间应力状态最大剪应力的大小及分布●掌握强度理论的概念及其适用范围【能力目标】●能熟练运用解析法和应力圆法求解一点处的应力状态●能求解空间应力状态下一点处的最大剪应力●能写出四个强度理论的相当应力及强度条件●能正确选择强度理论对构件危险点处进行强度校核第一节平面应力状态下的应力分析一、平面应力状态的概念由构件的应力分析可知,在受力构件的同一截面上不同点的应力是不同的,一般都既有正应力,又有切应力(如对称弯曲中,构件横截面上距中性轴为某一距离的任一点处)。
受力构件内一点处不同方位截面上应力的集合,称为一点处的应力状态。
为了研究受力构件内某一点处的应力状态,可以围绕该点取出一个单元体。
例如,研究图8—1(a)所示矩形截面悬臂梁内A点处的应力状态,可用三对相互垂直的平面,围绕图8—1若单元体有一对平面上的应力等于零,即不等于零的应力分量均处于同一坐标平面内,则称为二向或平面应力状态。
如受扭圆轴除轴线以外各点处及横力弯曲梁上下边缘以外各点处均为平面应力状态。
平面应力状态的普遍形式如图8—2(a)所示,即在其它两对平面上分别有正应力和切应力(σσxx,ττxx和σσyy,ττyy)。
现研究在普遍形式的平面应力状态下,根据单元体各面上已知的应力分量来确定其任一斜截面上的未知应力分量,并从而确定该点处的最大正应力及其所在截面的方位。
二、解析法(一)斜截面上的应力已知一平面应力状态单元体上的应力为σσxx,ττxx和σσyy,ττyy,如图8—2(a)所示。
如前所述,由于其前、后两平面上没有应力,可将该单元体用平面图形来表示(图8—2(b))。
为求该单元体与前、后两平面垂直的任一斜截面上的应力,可应用截面法。
设斜截面eeee的外法线nn与xx轴间的夹角(方位角)为α(图8—2(b)),简称为α截面,并规定从xx轴到外法线nn逆时针转向的方位角α为正值。
截面上的应力分量用σσαα和τταα表示。
图8—2利用截面法,沿斜截面eeee将单元体切成两部分,并取其左半部分eeeeee为研究对象。
设斜截面eeee的面积为dA,则截面eeee和eeee的面积分别为ddddddddddαα和ddddddss nnαα。
这样,微体eeeeee的受力如图8—2(c)所示,由该微体沿斜截面法向和切向的平衡方程,即∑FF nn=0和∑FF tt=0可得σσααdddd+(ττxx ddddddddddαα)ddss nnαα−(σσxx ddddddddddαα)ddddddαα+�ττyy ddddddss nnαα�ddddddαα−�σσyy ddddddss nnαα�ddss nnαα=0ττααdddd−(ττxx ddddddddddαα)ddddddαα−(σσxx ddddddddddαα)ddss nnαα+�ττyy ddddddss nnαα�ddss nnαα+�σσyy ddddddss nnαα�ddddddαα=0由切应力互等定理可知,ττxx和ττyy的数值相等(其指向已表示在图8—2(c)中)。
由此可得任一斜截面(α截面)上的应力分量为σσαα=σσxx+σσyy2+σσxx−σσyy2dddddd2αα−ττxx ddss nn2αα (8—1)τταα=σσxx−σσyy2ddss nn2αα+ττxx dddddd2αα (8—2) 以上两式就是平面应力状态下,任一α截面上应力σσαα和τταα的计算公式。
式中,正应力σσαα以拉应力为正,压应力为负;切应力τταα以其对单元体内任一点的矩为顺时针转向者为正,反之为负。
这与以前对正应力σσαα和切应力τταα的正负号规定是一致的。
(二)主应力和主方向式(8—1)和式(8—2)表明,任一斜截面的应力σσαα和τταα是随斜截面方位角α而变化的。
为求出σσαα的极值,令ddσσααddαα=−2�σσxx−σσyy2ddss nn2αα+ττxx ddss nn2αα�=0将上式与式(8—2)比较可知,正应力取极值的平面上的切应力为零,因此该平面就是主平面,正应力的极值就是主应力。
设主平面的方位角为αα0,由上式得tt tt nn2αα0=−2ττxxσσxx−σσyy (8—3) 由于tt tt nn2(αα0+90°)=tt tt nnαα0,所以式(8—3)可以给出两个相互垂直的主平面方位角αα0和αα0+90°。
将上述求得的两个方位角代入式(8—1),可求得两个主应力为σσmmttxx,mmss nn=�σσxx+σσyy2�±��σσxx−σσyy2�2+ττxx2 (8—4) 综上所述,σσαα的极值称为该点的主应力,σσαα取极值的微元面称为主平面,主平面的法线方向称为主方向,也称为应力的主轴,对应于两个不同主应力的主方向是相互垂直的。
主平面上切应力为零,反之,当某个微元面上的切应力为零时,该微元面上的正应力就是主应力,即切应力为零的微元面必定是主平面。
(三)最大切应力将式(8—2)对角α求导并令其为零,即ddττααddαα=�σσxx−σσyy�dddddd2αα−2ττxx ddss nn2αα=0设极值切应力所在平面的方位角为α1,由上式可得tt tt nn2αα1=σσxx−σσyy2ττxx(8—5)式(8—5)给出两个方位角α1和α1+90°,将这两个方位角代入式(8—2),可得两个极值切应力为ττmmttxx,mmss nn=±��σσxx−σσyy2�2+ττxx2 (8—6) 式(8—6)与式(8—4)比较,可得τmax=σmax−σmin2 (8—7) 即最大切应力等于两个主应力之差的一半,比较式(8—3)和(8—5),可得tt tt nn2αα1=−dddddd2αα0=tt tt nn2(αα0+45°)即有αα1=αα0+45°上式表明,切应力极值所在平面与主平面的夹角为45°。
二、几何法-应力圆法由公式(8—1)和(8—2)可知,平面应力状态下单元体α斜截面上的应力σσαα和τταα都是α的函数,这两个公式是α的参数方程。
为消去α可将上述公式改写为σσαα−σσxx+σσyy2=σσxx−σσyy2dddddd2αα−ττxx ddss nn2αατταα−0=σσxx−σσyy2ddss nn2αα+ττxx dddddd2αα将上述两公式各自平方后相加消去参数α,可得�σσαα−σσxx+σσyy2�2+(τταα−0)2=�σσxx−σσyy2�2+ττxx2 (8—8)从式8—8可见,在σσ−ττ直角坐标系内,随着斜截面方位角的变化其应力�σσαα,τταα�的轨迹是个圆,其圆心位于横坐标轴(σ轴)上,其横坐标为σσxx+σσyy2,半径RR=��σσxx+σσyy2�2+ττxx2,如图8—3所示。
该圆习惯上称为应力圆,或称为莫尔(O.Mohr)应力圆。
图8—3应力圆的做法是(如图8—4):1、建立以σσ为横轴、ττ为纵轴的坐标系。
在该坐标系中,找到点A�σσxx,ττxx�。
2、找到点A´�σσyy,ττyy�,由于ττyy=−ττxx,即A´�σσyy,−ττxx�。
AAˊ的连线与横轴的交点就是应力圆的圆心Oˊ。
3、以Oˊ为圆心,以O′A为半径作圆。
这个圆便是所求的应力圆。
应力圆周上的任意一点都代表了一个截面。
图8—4【例8—1】如图8—5所示,各单元体各面上的应力已知αα=30°,ββ=−30°。
请用应力圆的方法求解ab和ac两斜截面上的应力。
(c)图8—5解:根据单元体各面上的应力在σσσσττ坐标系中画应力圆,如图8—5(c)所示,图中应力单位为MPa。
几何计算可得圆心坐标为C(10,0),半径RR=50√2MMMMtt,φφ0=−135°。
ab截面(αα=30°)上的应力对应EE点坐标,其值为σα=σσOO����+RRdddddd�2α+φ0�=10+50√2dddddd(−85°)=28.3MMMMttτα=RRddss nn(2α+φ0)=50√2ddss nn(−85°)=−68.3MMMMttac截面(β=30°)上的应力对应EE’点坐标,其值为σβ=σσOO����+RRdddddd(2α+φ0)=10+50√2dddddd(−195°)=−58.3MMMMttτβ=RRddss nn(2α+φ0)=50√2ddss nn(−195°)=18.3MMMMtt主方向为αα0‘=−φφ02=67.5°(对应σσmmttxx),αα0"=ππ2−φφ02=−22.5°(对应σσmmss nn)第二节空间应力状态下的应力分析一、空间应力状态的概念对于受力物体内一点处的应力状态,最普遍的情况是所取单元体三对平面上都有正应力和切应力,其中切应力可分解为沿坐标轴方向的两个分量,这种应力状态即为一般的空间应力状态。
一般的空间应力状态有9个分量,根据切应力互等定理“在相互垂直的平面上,切应力成对存在且数值相等”可知,独立的应力分量有6个,分别用σσ1,σσ2,σσ3,ττxxyy,ττyyyy,ττxxyy表示。
二、任意截面上的应力空间应力状态是一点处应力状态中最为一般的情况,上节所讨论的平面应力状态可看作是空间应力状态的特例,即有一个主应力等于零。
仅一个主应力不等于零的应力状态,称为单轴应力状态。
空间应力状态所得的某些结论,也同样适用于平面或单轴应力状态。
图8—6 图8—7可以证明,在受力物体内的任一点处一定可以找到一个单元体,其3对相互垂直的平面均为主平面,三对主平面上的主应力分别为σσ1,σσ2,σσ3。
而且,与主应力σσ2(或σσ1)平行的各斜截面上的应力,可以由σσ1,σσ3(或σσ2,σσ3)确定的应力圆上的点表示,如图8—6所示。
进一步的研究证明,表示与三个主平面斜交的任意截面ABC上点D(图8—7所示)的应力σσ,ττ,必位于上述三个应力圆所围成的阴影范围以内。
其正应力和切应力分别为σσnn=σσ1dddddd2αα+σσ2dddddd2ββ+σσ3dddddd2γγ (8—9)ττnn=�σσ12dddddd2αα+σσ22dddddd2ββ+σσ3dddddd2γγ−σσnn2(8—10) 式中:αα、ββ、γγ分别是斜截面ABC的外法线和xx、yy、yy轴的夹角。