当前位置：文档之家 › 第7章-应力状态和强度理论03.

第7章-应力状态和强度理论03.

  • 格式：docx
  • 大小：494.44 KB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

材料力学第七章应力状态和强度理论

材料力学第七章应力状态和强度理论
2
x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y

x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2

x
y

2
4 2 xy
x
yx xy x
y
R c

x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2

40

x y
2 0.431MPa
sin( 80 ) xy cos(80 )

C
C

C
例题3：已知梁上的M、Q，试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q ＝ 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa

材料力学第七章_3_ 应变能密度和强度理论概要

材料力学第七章_3_ 应变能密度和强度理论概要

材料力学
第 7章 应力和应变分析·强度理论
[例9－8]证明弹性模量E 、泊松比µ 、切变弹性模量G 之间 的关系为 G E 。
2(1 )
证明： 纯剪应力状态应变能密度为
3
v1
1
2
1 2
2G
1 , 2 0, 3
1
用主应力计算比能
v2
1 2E
[
2 1
2 2
2 3
2 (1 2
2 3
1
3
k
1
3
2
OC
B
3
1
2
1 3
河南理工大学土木工程学院
A
材料力学
第 7章 应力和应变分析·强度理论
各向同性材料的广义胡克定律：
εx
1 E
σx
μ
σy
σz
εy
1 E
σy
μσz
σx
εz
1 E
σz
μ
σx σy
xy
xy
G
,
yz
yz
G
,
zx
zx
G
上述一组方程为用应力表示应变，若用应变表示应力，
河南理工大学土木工程学院

材料力学
第 7章 应力和应变分析·强度理论
二、常用四个强度理论
● 第一强度理论（最大拉应力理论） 该理论不论材料处于什么应力状态，引起材料脆性断裂
破坏的主要原因是最大拉应力，并认为当复杂应力状态的最 大拉应力达到单向应力状态破坏时的最大拉应力时，材料便 发生断裂破坏。由此，材料的断裂判据为
一、强度理论的概念
1. 什么是强度理论 强度理论是关于材料破坏原因的学说。

材料力学 第07章 应力状态分析与强度理论

材料力学 第07章 应力状态分析与强度理论
2
sin2a t xy cos2a
18/95
7.2 平面应力状态分析 主应力 7.2.3 主平面的方位及极值正应力 s x s y s x s y sa cos2a t xy sin2a 2 2 s x s y ds a 上式对a 求导 2 sin2a t xy cos2a da 2 s x s y 若a a0时，导数为 0 sin2a 0 t xy cos2a 0 0 2 2t xy tan2a 0 s x s y
7.2.5 应力圆
t
sx
tyx
sy
sx txy sy
D(sx,txy) 1. 确定点 D (s ,t ) x xy
O
D'(sy,tyx)
C
s
2. 确定点D' (sy,tyx) tyx= －txy 3. 连接DD'与s 轴交于点C 4. 以 C 为圆心，CD（CD'） 为半径画圆。
26/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆
sx sy sz
sxs1 100 MPas 2
0 MPas 3 120 MPa
11/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态 三个主应力中仅有一个主应力不为零 单向应力状态
s1
s1
F
A
F
12/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态
O
D'(sy,tyx)
C sx－ sx sy/2
s
27/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆 利用应力圆确定角a 斜截面上的正应力和切应力

工程力学c材料力学部分第七章 应力状态和强度理论

工程力学c材料力学部分第七章 应力状态和强度理论

无论是强度分析还是刚度分析，都需要求出应力的极值， 无论是强度分析还是刚度分析，都需要求出应力的极值，为了找 到构件内最大应力的位置和方向 需要对各点的应力情况做出分析。 最大应力的位置和方向， 到构件内最大应力的位置和方向，需要对各点的应力情况做出分析。
受力构件内一点处所有方位截面上应力的集合，称为一点的 受力构件内一点处所有方位截面上应力的集合，称为一点的 研究一点的应力状态时， 应力状态 。研究一点的应力状态时，往往围绕该点取一个无限小 的正六面体—单元体来研究。 单元体来研究 的正六面体 单元体来研究。
σ2
σ2
σ1
σ1
σ
σ
σ3
三向应力状态
双向应力状态
单向应力状态 简单应力状态
复杂应力状态 主应力符号按代数值的大小规定： 主应力符号按代数值的大小规定：
σ1 ≥ σ 2 ≥ σ 3
平面应力状态的应力分析—解析法 §7−2 平面应力状态的应力分析 解析法
图(a)所示平面应力单元体常用平面图形(b)来表示。现欲求 )所示平面应力单元体常用平面图形( )来表示。现欲求 垂直于平面xy的任意斜截面 上的应力 垂直于平面 的任意斜截面ef上的应力。 的任意斜截面 上的应力。
二、最大正应力和最大剪应力
σα =
σ x +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
τα =
令
σ x −σ y
2
sin 2α + τ x cos 2α
dσ α =0 dα
σ x −σ y
2
sin 2α +τ x cos2α = 0
可见在 τ α
=0

第七章+应力应变分析+强度理论

第七章+应力应变分析+强度理论
Chapter7 Analysis of Stress and Strain Failure Criteria
(Analysis of stress-state and strain-state)
§7-1 应力状态概述 (Introduction of stress-state)
一、应力状态的概念 (Concepts of stresses-state)
σ1 ≥ σ 2 ≥ σ 3
(Analysis of stress-state and strain-state)
三、应力状态的分类 （The classification of stresses-state）
1.空间应力状态（Triaxial stress-state or three-dimensional stress-state ） 三个主应力σ1 ,σ2 ,σ3 均不等于零 2.平面应力状态（Biaxial stress-state or plane stress-state） 三个主应力σ1 ,σ2 ,σ3 中有两个不等于零 3.单向应力状态（Uniaxial stress-state or simple stress-state） 三个主应力 σ1 ,σ2 ,σ3 中只有一个不等于零
x
− 62.5
σ3
因为 σx < σy ，所以 α0= 27.5°与σmin对应
σx −σ y 2 ⎧σ max σ x + σ y ⎧ 26MPa 2 ) + τ xy = ⎨ = ± ( ⎨ 2 2 ⎩ − 96MPa ⎩σ min σ 1 = 26MPa , σ 2 = 0, σ 3 = −96MPa
1.求单元体上任一截面上的应力（Determine the stresses on any inclined plane by using stress-circle） 从应力圆的半径 CD 按方位角α的转向转动2α得到半径CE. 圆周上 E 点的坐标就依次为斜截面上的正应力σα 和切应力τα.

材料力学第七章 应力状态

材料力学第七章 应力状态

主平面的方位：
tan
2a0
2 xy x
y
主应力与主平面的对应关系： max 与切应力的交点同象限
例题：一点处的平面应力状态如图所示。
已知 x 60MPa， xy 30MPa, y 40MPa, a 30。
试求（1）a 斜面上的应力； （2）主应力、主平面； （3）绘出主应力单元体。
x y cos 2a
2
x sin 2a
x
a
x y sin 2a
2
x cos 2a
300
10 30 2
10 30 cos 60020sin 600
2
2.32 MPa
300
10 30 sin 600 2
20cos 600
1.33 MPa
a
20 MPa
c
30 MPa
b
n1
y xy
a x
解：（1）a 斜面上的应力
y xy
a
x
2
y
x
2
y
cos 2a
xy
sin 2a
60 40 60 40 cos(60 ) 30sin(60 )
2
2
a x 9.02MPa
a
x
y
2
sin
2a
xy
cos
2a
60 40 sin(60 ) 30cos(60 ) 2
58.3MPa
2
1.33 MPa
300 600 x y 40 MPa
在二向应力状态下，任意两个垂直面上，其σ的和为一常数。
在二向应力状态下，任意两个垂直面上，其σ 的和为
一常数。
证明： a
x y

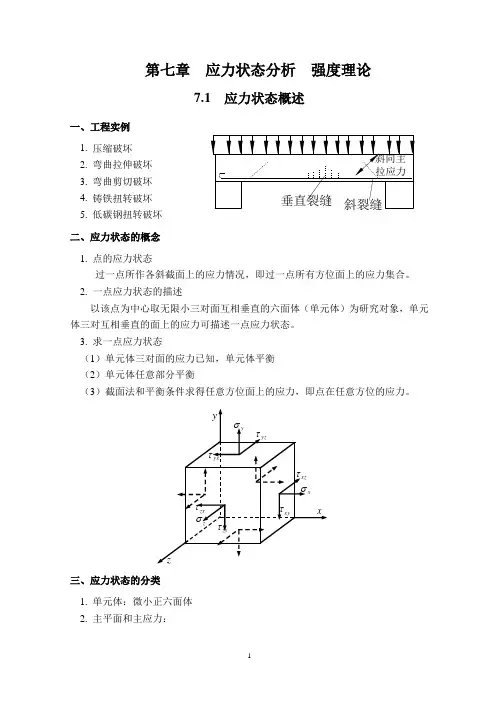
7-第七章 应力状态分析 强度理论.

7-第七章 应力状态分析 强度理论.

第七章应力状态分析强度理论7.1 应力状态概述一、工程实例1. 压缩破坏2. 弯曲拉伸破坏3. 弯曲剪切破坏4. 铸铁扭转破坏5. 低碳钢扭转破坏二、应力状态的概念1. 点的应力状态过一点所作各斜截面上的应力情况，即过一点所有方位面上的应力集合。

2. 一点应力状态的描述以该点为中心取无限小三对面互相垂直的六面体（单元体）为研究对象，单元体三对互相垂直的面上的应力可描述一点应力状态。

3. 求一点应力状态（1）单元体三对面的应力已知，单元体平衡（2）单元体任意部分平衡（3）截面法和平衡条件求得任意方位面上的应力，即点在任意方位的应力。

三、应力状态的分类1. 单元体：微小正六面体2. 主平面和主应力：主平面：无切应力的平面主应力：作用在主平面上的正应力。

3. 三种应力状态单项应力状态：三个主应力只有一个不等于零，如A 、E 点 二向应力状态：三个主应力中有两个不等于零，如B 、D 点 三向应力状态：三个主应力都不等于零四、应力状态分析的方法 1.解析法2. 图解法7.2应力状态分析的解析法一、解析法图示单元体，已知应力分量x σ、y σ、xyτ和yx τ。

xxx（一）任意截面上的正应力和切应力：利用截面法，考虑楔体bef 部分的平衡。

设ef 面的面积为dA ， ∑=0F n 0sin )Asin (cos )sin A (cos )cos A (sin )cos A (A =-+-+αασααταασαατσαd d d d d y yx x xy∑=0F tsin )Asin (cos )sin A (sin )cos A (cos )cos A (A =++--ααταασαασαατταd d d d d yx y x xy根据切应力互等定理： y x xy ττ=三角函数关系：22cos 1cos 2αα+=，22cos 1sin 2αα-=，∂=cos sin 22sin αα解得：ατασσσσσα2sin 2cos 22x x xy yy--++=（7-1）ατασστα2cos 2sin 2x xy y+-= （7-2）（二）主应力即主平面位置将式（8-1）对取一次导数，并令其等于零可确定正应力的极值和所在平面的位置。

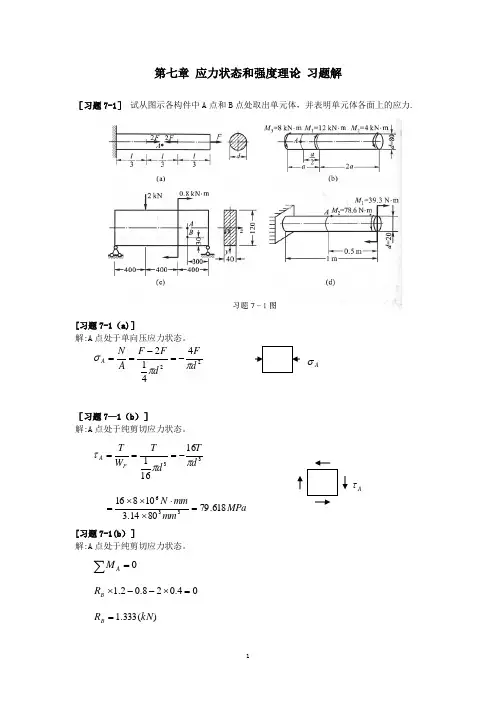
《材料力学》第7章-应力状态和强度理论-习题解

《材料力学》第7章-应力状态和强度理论-习题解
解：左支座为A，右支座为B，左集中力作用点为C，右集中力作用点为D。
支座反力: (↑)
=
（1）梁内最大正应力发生在跨中截面的上、下边缘
超过 的5。3％，在工程上是允许的。
（2）梁内最大剪应力发生在支承截面的中性轴处
(3)在集中力作用处偏外侧横截面上校核点a的强度
超过 的3.53%，在工程上是允许的。
解：坐标面应力:X（—0。05，0);Y（-0.2,0）
。根据以上数据作出如图所示的应
力圆。图中比例尺为 代表 。
按比例尺量得斜面的应力为：
按习题7—5得到的公式计算如下：
作图法(应力圆法)与解析法（公式法）的结果一致。
［习题7-7]试用应力圆的几何关系求图示悬臂梁距离自由端为 的截面上，在顶面以下 的一点处的最大及最小主应力,并求最大主应力与 轴之间的夹角。
解：
…………(1)
…………（2)
（1)、(2)联立,可解得 和 。
至此,三个面的应力均为已知：X（ ，0），Y（ ，0）（ , 均为负值）;
( ）。由X，Y面的应力就可以作出应力圆。
[习题7-12]一焊接钢板梁的尺寸及受力情况如图所示,梁的自重略去不计。试示 上 三点处的主应力。
解:（1）求 点的主应力
解：坐标面应力：X（15,15）,Y(0，-15）
第一强度理论：
因为 ， ，即 ，
所以 符合第一强度理论的强度条件，构件不会破坏，即安全.
第二强度理论：
因为 ,
，即 ，
所以 符合第二强度理论的强度条件，构件不会破坏，即安全。
[习题7—25]一简支钢板梁承受荷载如图a所示，其截面尺寸见图b。已知钢材的许用应力为 , .试校核梁内的最大正应力和最大切应力。并按第四强度理论校核危险截面上的a点的强度。注:通常在计算a点处的应力时，近似地按 点的位置计算。

第七章_应力状态和强度理论

第七章_应力状态和强度理论

第 1 页/共 4 页第七章 应力状态和强度理论7-3 横截面上 AF =σ α截面上 αστασσσαα2sin 22cos 22=+=，强度条件 ][432sin 2][)2cos 1(2σατσασαα≤=≤+=A F A F ，等价于 ][2sin 342)2cos 1(2max σαασ≤⎭⎬⎫⎩⎨⎧⋅+=A F A F e ，由0=ασd d e，并比较︒=0α或︒60的e σ，得使e σ最小的角度︒=60α 7-7 内力 m kN M ⋅-=2.7，kN F s 10-=应力 MPa I Myz 55.10==σ，MPa bI S F z z s 88.0*-==τ 主应力 MPa 62.1022221=+⎪⎭⎫⎝⎛+=τσσσ，MPa 073.022223-=+⎪⎭⎫⎝⎛-=τσσσ主平面方位 ︒=⇒=-=74.4167.022tan 00αστα7-8(d) MPa MPa x y x 50200-=-==τσσ，， ︒=45α截面上：MPaMPax yx yy102cos 2sin 2402sin 2cos 22=+-==--=αταστατασσσαα主应力：MPa x y y4122221=+⎪⎪⎭⎫ ⎝⎛+=τσσσ， MPa x y y6122223-=+⎪⎪⎭⎫ ⎝⎛-=τσσσ主平面方位：︒=⇒=--=34.39522tan 00ασταyx7-15(a) MPa z 50=σ——为主应力，另两个主应力由下列应力决定 MPa MPa MPa x y x 403070-===τσσ，，MPa MPa x y x yx x y x yx 3.5227.94222222=+⎪⎪⎭⎫ ⎝⎛--+=''=+⎪⎪⎭⎫ ⎝⎛-++='τσσσσστσσσσσ主应力 MPa MPa MPa z 3.5507.94321=''===='=σσσσσσ，， 最大切应力 MPa 7.44231max =-=σστ7-16(a) MPa MPa MPa 105070321＝，＝，＝σσσ A 点：MPa MPa A A 2030==τσ，在2σ与3σ决定的应力圆上使切使劲达极值7-18 立方体边长 a ＝20mm不计摩擦，各面上的应力为主应力顶面 MPa aF3523-=-=σ，侧面021<=σσ 主应变021==εε，又)]([13211σσνσε+-=EMPa 151321-=-==⇒σννσσ7-21 k 处截面上的内力： e M laM =，l M F e s =应力： bhFb I S F s z z s 230*==＝，τσ︒=45α方向即为主应力方向第 3 页/共 4 页τστσ-==31，主应变 )(131451νσσεε-==︒E由上可得 ︒+=45)1(32ενElbhM e7-22 钢球各点应力状态相同 MPa 14321-===σσσ体应变 )(21321σσσνθ++-=E体积改变 3101054.6m V V -⨯==∆θ7-23 MPa MPa MPa z y x 403070-===σσσ，，MPaMPax y x y x x y x y x 28.54)(21)(2172.944)(21)(212222=+--+=''=+-++='τσσσσστσσσσσ主应力 MPa MPa MPa 28.55072.94321==σσσ，＝， []3213232221/99.12)()()(61m m kN Ev d ⋅=-+-+-+=σσσσσσν7-24 平面应力状态 MPa MPa x y x 15015===τσσ，，主应力 MPa MPa x x x27.9027.242232221-===+⎪⎭⎫ ⎝⎛+=σστσσσ，， 按第一强度理论：][11t r σσσ<= 按第二强度理论：][59.26)(3212t r MPa σσσνσσ<=+-= 满意强度条件。

第七章 应力状态、应变分析和强度理论

第七章 应力状态、应变分析和强度理论

§7-3 平面应力状态分析－－解析法
二、 正应力极值
1 1 ( x y ) ( x y ) cos 2 xy sin 2 2 2 d ( x y ) sin 2 2 xy cos 2 d
设α＝α0 时，上式值为零，即
2
1 0, 2 0, 3 0
1 0, 2 0, 3 0
§7-1 应力状态的概念
3、三向（空间）应力状态 三个主应力1 、2 、3 均不等于零
2 1
3 1
3 2
1 0, 2 0, 3 0
§7-1 应力状态的概念
仅在微体四侧面作用应力，且 应力作用线均平行于微体的不 受力表面－平面应力状态
1
1
1
1
3
3
1 0, 2 0, 3 0
1 0, 2 0, 3 0
§7-1 应力状态的概念 2、二向（平面）应力状态 三个主应力1 、2 、3 中有两个不等于零
3 2 3 2
3
2
1
3
1
1
1
1 0, 2 0, 3 0
Ft 0
dA ( x dAcos )cos ( x dAcos )sin ( y dAsin )sin ( y dAsin )cos 0
§7-3 平面应力状态分析－－解析法
一、任意斜截面上的应力公式 已知： x , y , x , y , dA 求： ，
sin 2 xy cos 2
2 xy 2 ( 50) tan 2 0 1 x y 40 60 2 0 45 135

y =60 MPa xy = -50MPa =-30°

应力状态理论与强度理论

应力状态理论与强度理论

D，承受内压 p 作用。
FN
A
p D2
p 4
p Dt
pD 4t
1
2
pD 4t
3 p 0
实例四 圆杆受扭转和拉伸共同作用
m
P
P
m
FN 4 P
A pd2
T 16m Wt p d 3
按工程应用传统观念，判断构件强度取 决于危险点的应力状态。
危险点是怎样达到破坏的呢？
在什么方向最容易破坏呢？
剪应力（应力单位为MPa）。
20
40
50 30
解：
max 30 20
min
2
30 + 20 2 2
+ 402
52.2 MPa
42.2
1 52.2MPa
20
2 50MPa
40
3 42.2MPa
max
1
3
2
47.2MPa
30
50
例6、求图示应力状态的主应力和
最大剪应力（应力单位MPa）。
第七章 应力状态理论与强度理论
本章重点 1、应力状态的概念 2、如何建立一点处的应力状态 3、平面应力状态分析 4、广义胡克定律 5、强度理论的概念 6、四种主要强度理论及其应用
问题的提出：
铸铁
低碳钢
思考：塑性材料拉伸时为什么会出现滑移线？
低碳钢
铸铁
思考：为什么脆性材料扭转时沿45º螺旋面断开？
P
解：刚性凹座是不变形的
Nx
Nz Ny
Nx
Ny
x y 0
Nx
x
1 E
x
(
y
+ z )
0
y

材料力学 第七章 应力状态和强度理论

材料力学 第七章 应力状态和强度理论

y
2
2 xy
tan 2a0
2 xy x
y
max
1
2
3
主应力符号与规定： 1 2 3 （按代数值）
§7-3 空间应力状态
与任一截面相对应 的点，或位于应力 圆上，或位于由应 力圆所构成的阴影 区域内
max 1 min 3
max
1
3
2
最大切应力位于与 1 及 3 均成45的截面上
针转为正，顺时针转为负。
tg 2a 0
2 x x
y
在主值区间，2a0有两个解，与此对应的a0也有两个解，其中落
在剪应力箭头所指象限内的解为真解，另一解舍掉。
三、应力圆
由解析法知，任意斜截面的应力为
a
x y
2
a x
x
y
2
y cos2a
2
sin 2a x c
x s os2a
in
2a
广义胡克定律
1、基本变形时的胡克定律
1）轴向拉压胡克定律
x E x
横向变形
y
x
x
E
2）纯剪切胡克定律
G
y
x x
2、三向应力状态的广义胡克定律－叠加法
2
2
1
1
3
3
1
1
E
2
E
3
E
1
1 E
1
2
3
同理
2
1 E
2
3
1
广义胡克定律
3
1 E
3
1
2
7-5, 7-6
§7-4 材料的破坏形式
⒈ 上述公式中各项均为代数量，应用公式解题时，首先应写清已 知条件。

第7章-应力状态和强度理论03

第7章-应力状态和强度理论03

3）最大切应力理论(第三强度理论)
假设最大切应力max是引起材料塑性屈服的因 素，则：
max jx
对低碳钢等塑性材料，单向拉伸时的屈服是 由45°斜截面上的切应力引起的，因而极限应力 jx可由单拉时的屈服应力求得，即：
jx
因为： max
ss
2
常数
s1 s 3
对图示平面应力状态，不能分别用
s max [s ]
max [ ]
来建立，因为s与之间会相互影响。 研究复杂应力状态下材料破坏的原因，根据一 定的假设来确定破坏条件，从而建立强度条件，这 就是强度理论的研究内容。
4）材料破坏的形式 常温、静载时材料的破坏形式大致可分为： • 脆性断裂型： 例如： 铸铁：拉伸、扭转等； 低碳钢：三向拉应力状态。 • 塑性屈服型： 例如： 低碳钢：拉伸、扭转等； 铸铁：三向压缩应力状态。 可见：材料破坏的形式不仅与材料有关，还与 应力状态有关。


单拉： s r 4 3 s s s 由此可得： s
1
3 [ ] 0.577[s ] 0.6[s ]
s s 0.577s s
例：两端简支的工字钢梁承受荷载如图a所示。已 知材料（Q235钢）的许用应力为[s]=170MPa和[]= 100MPa。试按强度条件选择工字钢号码。
W 508 10 m
6
3
再按切应力强度条件进行校核。对28a号工 字钢，查表可得截面几何性质为：
I z 71.14 10 6 m 4
Iz S z ,max
d 0.85 10 m
2
24.62 10 2 m
中性轴处的最大切应力（纯剪应力状态）为：
max

材料力学第七章

材料力学第七章

若应力状态由主应力表示，并且在max 0 和 min 0 的情况下，则式（7-7） 成为
max min
max
min
2
1 3
2
进一步讨论，由式（7-4）和式（7-6）可知
tan
21
1 tan 20
上式表明1 与 0 之间有如下关系：
1
0
4
可见，切应力取得极值的平面与主平面之间的夹角为 45 。
若三个主应力中，只有一个主应力不等于零，这样的应力状态称为 单向应力状态。若三个主应力中有两个不等于零，称为二向应力状态或 平面应力状态。若三个主应力皆不为零，称为三向应力状态或空间应力 状态。
第二节 平面应力状态分析——解析法
一、斜截面上的应力
图 7-1 所示为平面应力状态的最一般情况。已知 x ， y ， xy 和 yx 。现 在研究图中虚线所示任一斜截面上的应力，设截面上外法向 n 与 x 轴的夹角 为 。
令 d /d 0 ，由式（7-1）可得
x
2
y
sin
2
xy
cos 2
0
解得
（7-3）
tan 20
2 xy x y
通过运算，可以得到斜截面上正应力的极值为
（7-4）
max min
x
y 2
x
2
y
2
2 xy
（7-5）
由式（7-4）可知， 取得极值的角0 有两个，二者相差 90 ，即最大正应 力 max 和最小正应力 min ，二者分别作用在两个相互垂直的截面上。当 0 ， 取得极值时，该斜截面上的切应力 0 ，即正应力就是主应力。
（a）
（b） 图7-6
例 7-4 悬臂梁受力如图 7-7（a）所示。试求截面 n n 上 A 点处的主应力 大小和方向，并按主平面画出单元体。

材料力学 第七章 应力状态与强度理论

材料力学 第七章 应力状态与强度理论

取三角形单元建立静力平衡方程
n 0
dA ( xdA cos ) sin ( xdA cos ) cos ( y dA sin ) cos ( y dA sin ) sin 0
t 0
dA ( xdA cos ) cos ( xdA cos ) sin ( y dA sin ) sin ( y dA sin ) cos 0
2 2

cos 2 x sin 2
2 x y 2 x y ( ) ( cos 2 x sin 2 )2
2
2

x y
sin 2 x cos 2
( 0) (
x y
2
2
sin 2 x cos 2 )
max x y x y 2 x 2 2 min
2
max
1 3
2
例7-2 试求例7-1中所示单元体的主应力和最大剪应力。
（1）求主应力的值
x 10MPa, y 30MPa, x 20MPa max x y x y 2 2 x min 2
复杂应力状态下（只就主应力状态说明） 有三个主应力
1 , 2 , 3
1
E
由 1引起的线段 1应变 1
由 2引起的线段 1应变 1
2
由 3引起的线段1应变 1
3
E
E
沿主应力1的方向的总应变为：
1 1 1 1
1 42.4 1 3 2 0 MPa 由 max 3 2.4 2

知识资料材料力学知识资料应力状态分析和强度理论(三)组合变形压杆稳定(新版)

知识资料材料力学知识资料应力状态分析和强度理论(三)组合变形压杆稳定(新版)

需要课件请或强度理论（一）强度理论的概念1．材料破坏的两种类型材料破坏型式不仅与材料本身的材质有关，而且与材料所处的应力状态、加载速度温度环境等因素有关。

材料在常温、静载荷下的破坏型式主要有以下两种：脆性断裂材料在无显然的变形下骤然断裂。

塑性屈服(流动) 材料浮上显著的塑性变形而丧失其正常的工作能力。

2．强度理论在复杂应力状态下关于材料破坏缘故的假设，称为强度理论。

研究强度理论的目的，在于利用容易应力状态下的实验结果，来建立材料在复杂应力状态下的强度条件。

（二）四个常用的强度理论四个常用强度理论的强度条件可以统一地写成式中σr称为相当应力，其表达式为最大拉应力理论σr1＝σ1(第一强度理论)最大拉应变理论σr2＝σ1－ν(σ1+σ2)(第二强度理论)最大剪应力理论σr3＝σ1－σ3(第三强度理论)形状改变比能理论(第四强度理论)[σ]为材料的许用应力。

第1 页/共18 页对于工程上常见的一种二向应力状态如图5—9—3所示，其特点是平面内某一方向的正应力为零。

设σy=0，则该点的主应力为代入(5—9-15)式得：第三强度理论(最大剪应力理论)的相当应力为第四强度理论(形状改变比能理论)的相当应力为最大拉应力理论、最大拉应变理论是关于脆性断裂的强度理论；最大剪应力理论、形状改变比能理论是关于塑性屈服的强度理论。

强度理论的选用在三向拉应力作用下，材料均产生脆性断裂，故宜用第一强度理论；而在三向压缩应力状态下，材料均产生屈服破坏，故应采用第三或第四强度理论。

当材料处于二向应力状态作用下时：脆性材料易发生断裂破坏，宜用第一或第二强度理论；塑性材料易发生塑性屈服破坏，宜用第三或第四强度理论。

[例5-9-1] 已知构件上某点的应力单元体如图5-9-4(a)，(b)所示(图中应力单位为MPa)。

试求指定斜截面上的应力。

[解] 图示单元体处于平面应力状态。

(1)在图示坐标中代人公式(5-9-1)、(5-9-2)得σα、τσ方向如图中所示。

材料力学-07-应力分析和强度理论

材料力学-07-应力分析和强度理论

§7-2 平面应力状态 平面应力状态--解析法 平面应力状态 解析法： 解析法
1.斜截面上的应力 1.斜截面上的应力
y
σx
a
τ yx
τ xy
σx α
τa
n
τ xy
σa
dA
x
σy
n
τ yx
σy
t
t
∑F = 0
∑F =0
13
§7-2 平面应力状态 平面应力状态--解析法 平面应力状态 解析法： 解析法
tan 2α0 = − 2τ xy
σ x −σ y
由上式可以确定出两个相互垂直的平面， 由上式可以确定出两个相互垂直的平面，分别 为最大正应力和最小正应力所在平面。 为最大正应力和最小正应力所在平面。 所以，最大和最小正应力分别为： 所以，最大和最小正应力分别为：
σmax = σ x +σ y
2 1 + 2 − 1 2
单元体
单元体——构件内的点的代表物， 单元体——构件内的点的代表物，是包围被研究点的 ——构件内的点的代表物 无限小的几何体。 常用的是正六面体。 无限小的几何体。 常用的是正六面体。 单元体的性质—— 平行面上，应力均布； 单元体的性质——1) 平行面上，应力均布； —— 2) 平行面上，应力相等。 平行面上，应力相等。
2 2
σy
τ xy
α
60 − 40 60 + 40 = + cos(−60o ) + 30 sin(−60o ) 2 2
σx
= 9.02 MPa
τα =
σ x −σ y
2 60 + 40 = sin(−60o ) − 30 cos(−60o ) 2

第七章：应力状态、强度理论

第七章：应力状态、强度理论

s
2 2
s
2 3
2 s1s 2
s 3s 2
s1s 3 )
1 t 2 0 (t )2 2 0 0 t (t ))
2E
s1
1 t 2
E
G
E
21
)
§7–6 强度理论及其相当应力
强度理论：是关于“材料发生强度破坏或失效”的假设
材料的破坏形式： ⑴ 脆性断裂 如铸铁在拉伸和扭转时的突然断裂 ⑵ 塑性屈服 如低碳钢在拉伸和扭转时明显的塑性变形
sx
t 绕研究对象顺时针转为正；
y
txy
逆时针为正。
Ox
图1
s
sx
y
sy
ttxy
Ox 图2
设：斜截面面积为dA，由分离体平衡得：
Fn 0
n s dA (t xydAcos )sin (s xdAcos ) cos t (t yxdAsin ) cos (s ydAsin )sin 0
容器表面用电阻应变片测得环向应变 t =350×10-6，若已知容器平均 直径D=500 mm，壁厚=10 mm，容器材料的 E=210GPa，=0.25
试求:1.导出容器横截面和纵截面上的正应力表达式； 2.计算容器所受的内压力。
s1 sm
p p
p
x
l
图a
D
y
xp
AO
B
解：容器的环向和纵向应力表达式 1、轴向应力:(longitudinal stress) 用横截面将容器截开，受力如图b所示,根据平衡方程
第七章 应力状态和强度理论
§7–1 概述 §7–2 平面应力状态的应力分析.主应力 §7–3 空间应力状态的概念
§7–4 复杂应力状态下的应力 -- 应变关系 ——（广义虎克定律）
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

西南交it 大学应用力*与工程系材#^力学教研i图示拉伸甄压缩的单向应力状态，材料的破 坏有两种形式：塑性屈服；极限应力为0■力=<5；或bpO2 腌性斷裂；极限应力为O ■必= CJ\ 此时，4 O>2和偽可由实验测得.由此可建 互如下S 度余件：^mai其中n 为安全系数•2）纯剪应力状态：图示纯剪应力狀态，材料的破 坏有两种形式：塑性屈服：极限应力为 腌性斯裂：极限应力为5 = 5%和昭可由实验测得.由此可建立如下=(^■1it§7.7强度理论及其相当应力1、概述1）单向应力状态:a.＜亠［6 n其中, »度条件:前述a 度条件对材料破坏的原因并不深究.例如 图示低碳钢拉（压）时的强度条件为：r V J - b, b|nw W — — —// n然而，其屈服是由于 YnurJl 起的,对®示单向 应力状态，有： 「niu依照切应力强度条件，有：<Ln可见，O •女=6与 相当（等效）•3）复杂应力状态对图示平面应力状态，不能分别用 q仏5⑺来建立，因为＜7与点间会相互影响.研究复杂应力状态下材料破坏的原因，根据一 定的假设東确定破坏条件，从而建立强度条件，这 就是《度理论的研究内客. QCdJ例如， 二由于 :单J — 26= 6=1 ，24）材料破坏的形式常温、静栽时材料的破坏形式大致可分为:•腌性斷裂型：例如：铸铁：拉伸、扭转等； "钢：三向拉应力状态.-塑性屈月艮型：例如：低碳钢：拉伸、扭转寻；铸铁：三向压缩应力状态.可见：材料破坏的形式不仅与材料有关，还与应力状态有关. ,5）强度理论根据一些实验资料，针对上述两种破坏形式，分别针对它们发生破坏的原因提出假说，并认为不论材料处于何种应力状态，某种类型的破坏都是由同一因素引起，此即为强度理论.常用的破坏判据有：旎性断裂：5,磁可皿«性斷裂：V；下面将讨论常用的-基于上述四种破坏判据的»虞理论.2s四个常用的强度理论1）最大拉应力理论（第一S度理论）假设最大拉应力5是别起材料脆性断裂的因 *.不论在什么样的庖力状态下，只要三个主应力中的最大拉应力5达到极限应力巧工，材料就发生旎性断裂，即：cr.强度条件：5 <-^ = lcr]H可见：3）与6*巧无关；b）应另巧』命用单向拉伸试样发生旎性断裂的/ 试验来确定. ‘4 QC回实验验证：铸铁：单拉、纯剪应力状态下的破坏与该理论相符；平面应力状态下的破坏和该理论基本相符.存在问题：没有考虑6, 6对脆斷的彫响，无法解释石料单压时的纵向干裂现;象，2）最大伸长线应变理论（第二强度理论）假设最大伸长线庖变£是引起腌性破坏的主要因素，I'J:号，用单向拉伸测定，即：QC回因 :CT, - ^(0-2 十 crj= O •“莊度条件为：cr,-p(cr2 + cr3)< —= [a]n实脸验证：a ） 可解释大理石单压时妁纵向裂縫；b ） 铸铁二向、三向拉应力状态下的实脸不符；£）对铸铁一向拉、一向压的二向应力状态偏于 安全，但可用.L^UEl3）最大切应力理论（第三後度理论）假设最大切应力q 応是引起材料塑性扈服的因 素，则：几 W. = J对低碾钢等塑性材料，单向拉伸时的屈服是 由45。

斜截面上的切应力引起的，因而极限应力 号X 可由单拉时的屈服应力求得，即： 巧「=守=常数L^UEl因为: ® =-(5 7(6 + bj) 匕 因为：「皿=%㊁空IlUX由此可得，黑度条件为："-辱仝=[6/I实验验证：a）仅适用于拉压牲能相同的材*H b）低决钢单拉（压）对45。

滑移线吻合；C）二向应力状态基本符合，偏于安全.存在问題：3）没考虑6对屈服^的彩响，偏于安全，但谋差较大；b）仅适用于拉压性能相同的材料.and4）形状改变能密度理论（笫四弓更度理论）假设形状改变能密度吃是引起材料塑性屈服的因素，即：y （叽（5）由可通过单拉试验来确定.因为材料单担屈服时有：5=6 b, =b3 =0心护2切所以:又：儿二罟治]-oJ' + GyJ +（6-<73）']and因此：£[（6 Y J +（幻一6）' +（6 Y J]=6由此可得强度条件为：实验验证：a）较第三》度理论更接近实际值;b）材料拉压性能相同时成豆•£[& -bpF+(6 Y J+(5 -<T J CTS 亠»度理论的统一形式：6 <Qj6称为相当应力，分别为：-最大拉应力（第一强度）理论：6（=6-最大伸长线应变（第二强度）理论：62 = 5 -“（6+5）-最大切应力（第三良度）理论：63=5-6・形狀改变能密度（第四S度）理论：f 二- D J+（5 - 5 F+（巧- 5）•莫尔孫度理论：应用范围：a ） 仅适用于常温.蒔载条件下的均匀、连续，各 向同性的材料；b ） 不论塑性或腌性材*h 在三向拉应力状态都 发生脆性斷裂，宜采用第一强度理论；C ）对于腌性材料，在二向拉应力状态下宜采用第 一强度理论；d ） 对塑牲材料，除三向拉应力状态外都会发生 屈服，宜采用第三或第四强度理论；e ） 不论塑性或腌性材料，在三向压应力状态都发J 生屈服失效，宜釆用第四强度理论.例：两危险点的应力状态如图，（7 =r»由第三、 四强度理论分别比较其危险程度•解：对图ii 所示应力状态，因为§7,8强度理论的应用<a > <b所以: b2 = 06詣-J y] +宀*G-辰)63 = 6-6 = 2. J64 二J* Ski - (7 J + (刃-屯)2 +(6 - CT J =y/a^ +3r^ =2a对图b所示应力状态，有:6 =-C7所以：刁4=J+b-(7/+(6=2<T-bj +(6 -bj ]I可见：由第三强度理论，图b 所示应力状态比 图0所示妁安全；而由第四强度理论，两者的危险 程度一样.注意：图a 所示应力状态实际上为拉扭和弯扭组 合加载对应的应力状态，其相当应力如下：可记住，便于组合变形的强度校核.L^UEl例：利用第三或第四强度理论求纯剪应力状态下屈 服应力耳和拉压屈服应力q 之间的关系.解：图示纯剪应力状态的主应力为： b, =T cr^ =0 CTj = —r 当"盂时材料发生屈服，因此有:5 = G 6=06 =由第三强度理论，有：b” =6 -<7, = 2.而当材料拉压屈服时有：0 = 6L^UElT即， bF3=CT$由此可得：=0.5o\ [r) = {).5|crl 利用第四S 度理论，有：纯剪：S = * [C| — b J + C 2 - ^3 )2 +(5 - b J =血$单拉：丐4=cr. 由此可得：J = = 0.577 cr^ [rl=O.577fcrl^().6fcrl例:两端简支的工字钢梁承受荷载如图a 所示.已 知材料(0235朝)的许用应力为|c71=17«MPa 和冷= I00MPii ・试按强度条件选择工字钢号码.⑴2(K) kN 200 kN 解：首先确定钢梁的危险截面• 3*作出梁的剪力图和弯 一蔻图如图b 和图£所示，可 见C 、D 截面为危险截面， 取C 栽面计算，其剪力和 弯矩为： /^r = ^nax=200kNMcWmx =84kN IrT^200 kN (b)2W*N■1 200 kN DI (ifc m(C) MIU MkNm2«)kN 4先按正应力强度条件选择截面型号.因最大 正应力发生在<7截面的上、下边缘处，且为单向 应力状态，由正舷力强曲卅可得截面系数为： —_81^=4心0 缶■ [<7] 170 X10** 据此可选用2811号工字钢，其截面系数为；W = 508xl0"n?再按切应力孑Ji 度条件进行校核・对轴号工 字钢，查表可得截面几何性质为：/ =71,l4xl0'%n^/ C , —— = 24.62 X 10 "m d = ().85 XI Of S 沁中性轴处的最大切应力(纯剪应力状态)为：二伦皿二皿二200x1()3_ ~/.Xt/~* 24.62x10 ^xO.85xlO^^ = 95.5MPa<trJ = lOOMPa 可见，选用2血号工字钢满足切应力强度条件, 简化的截面形状和尺寸以及应力分布如图d 所示.<d).max 了 nux以上分析仅考虑了最大正应力和切应力作用的位暨，而对工字型截面腹板和具嫌交界处(图d中的Q点),正应力和切应力都较大，且处于平面应力状态(见图e),因此还需对此进行强度校核.(e)r：:d••J利用图d所示的截面简化尺寸和已有的4,可求得a点的正应力O和切应力松别为：L^UElJ』E5：63j49.]MPa<7 = rax -■7. 71.14x1()"”空仝=22竺怦空=738MPJ /.J 71.14xIO"'xO.O()85 其中，$二为横截面的下缘面积对中性轴的静飓，为：( 0()门7、5. = 0.122 X 0.0137 x [(11263 一； J= 223xl(r&n?由前例可得，图e所示应力状态的第四强度理论相当竝力为：L^UEl⑰=2+2 = A/|49.1-+3x73.8-= 196.4MPa>[cr| = l 7()M Pa可见，28ii号工字钢不能满足要求.改用28b 号工字钢，按同样的方法可得：S = 173.2MPn<l/Tly|.O5 = l78.5MPn_ J注意：本例中对应点的僅度校核是按简化后的 截面尺寸进行的.实际上，对符合国家标准的型钢并不需要对该点进行校核；然而，对自行设计 的焊接而成的组合工字案则需进行校核.b/S = Jy 十 4厂2请自行计算肢终结果.。