当前位置：文档之家 › 第七章应力状态和强度理论详解

第七章应力状态和强度理论详解

  • 格式：ppt
  • 大小：3.93 MB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

材料力学第七章应力状态和强度理论

材料力学第七章应力状态和强度理论
2
x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y

x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2

x
y

2
4 2 xy
x
yx xy x
y
R c

x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2

40

x y
2 0.431MPa
sin( 80 ) xy cos(80 )

C
C

C
例题3：已知梁上的M、Q，试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q ＝ 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa

C07应力状态和强度理论

C07应力状态和强度理论
7.5 三向应力状态
x平面上有正应力sx, 切 应力txy, 和txz。切应力
的两个下标中, 第一个 下标表示切应力所在 平面, 第二个下标表示 切应力的方向。
同理y平面上有正应力
sy, 切应力tyx, 和tyz; z 平面上有正应力sz, 切 应力tzx, 和tzy。
7.5 三向应力状态
在一般的空间应力 状态的9个应力分量 中, 根据切应力互等 定理, 在数值上有txy ＝tyx, txz＝tzx, tyz＝ tzy, 因 而 , 独 立 的 应 力分量是6个, 即sx, sy, sz, txy, tyz和tzx。
G
,
g yz
t yz
G
,
g zx
t zx
G
7.8 广义虎克定律
一般空间应力状态下, 在线弹性范围内、小变形 条件下各向同性材料的广义胡克定律:
ex
1 E
[s x
m(s
y
sz
)]
e
y
1 E
[s
y
m(s z
s x )]
ez
1 E
[s
z
m(s x
s y )]
g xy
t xy
G
,
g yz
t yz
G
,
g zx
s3
O
s3
s
O
z
x
s2
s1
整个单元体内的最大切应力为:
t max
s1 s3
2
7.5 三向应力状态
t
y
s2
tmax
s3
O z
D
s1
O
s
s3
x
s2
s1

材料力学 第07章 应力状态分析与强度理论

材料力学 第07章 应力状态分析与强度理论
2
sin2a t xy cos2a
18/95
7.2 平面应力状态分析 主应力 7.2.3 主平面的方位及极值正应力 s x s y s x s y sa cos2a t xy sin2a 2 2 s x s y ds a 上式对a 求导 2 sin2a t xy cos2a da 2 s x s y 若a a0时，导数为 0 sin2a 0 t xy cos2a 0 0 2 2t xy tan2a 0 s x s y
7.2.5 应力圆
t
sx
tyx
sy
sx txy sy
D(sx,txy) 1. 确定点 D (s ,t ) x xy
O
D'(sy,tyx)
C
s
2. 确定点D' (sy,tyx) tyx= －txy 3. 连接DD'与s 轴交于点C 4. 以 C 为圆心，CD（CD'） 为半径画圆。
26/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆
sx sy sz
sxs1 100 MPas 2
0 MPas 3 120 MPa
11/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态 三个主应力中仅有一个主应力不为零 单向应力状态
s1
s1
F
A
F
12/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态
O
D'(sy,tyx)
C sx－ sx sy/2
s
27/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆 利用应力圆确定角a 斜截面上的正应力和切应力

工程力学c材料力学部分第七章 应力状态和强度理论

工程力学c材料力学部分第七章 应力状态和强度理论

无论是强度分析还是刚度分析，都需要求出应力的极值， 无论是强度分析还是刚度分析，都需要求出应力的极值，为了找 到构件内最大应力的位置和方向 需要对各点的应力情况做出分析。 最大应力的位置和方向， 到构件内最大应力的位置和方向，需要对各点的应力情况做出分析。
受力构件内一点处所有方位截面上应力的集合，称为一点的 受力构件内一点处所有方位截面上应力的集合，称为一点的 研究一点的应力状态时， 应力状态 。研究一点的应力状态时，往往围绕该点取一个无限小 的正六面体—单元体来研究。 单元体来研究 的正六面体 单元体来研究。
σ2
σ2
σ1
σ1
σ
σ
σ3
三向应力状态
双向应力状态
单向应力状态 简单应力状态
复杂应力状态 主应力符号按代数值的大小规定： 主应力符号按代数值的大小规定：
σ1 ≥ σ 2 ≥ σ 3
平面应力状态的应力分析—解析法 §7−2 平面应力状态的应力分析 解析法
图(a)所示平面应力单元体常用平面图形(b)来表示。现欲求 )所示平面应力单元体常用平面图形( )来表示。现欲求 垂直于平面xy的任意斜截面 上的应力 垂直于平面 的任意斜截面ef上的应力。 的任意斜截面 上的应力。
二、最大正应力和最大剪应力
σα =
σ x +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
τα =
令
σ x −σ y
2
sin 2α + τ x cos 2α
dσ α =0 dα
σ x −σ y
2
sin 2α +τ x cos2α = 0
可见在 τ α
=0

材料力学应力和应变分析强度理论

材料力学应力和应变分析强度理论

§7–5 广义虎克定律
y
一、单拉下旳应力--应变关系
x
x
E
y
E
x
ij 0 (i,j x,y,z)
二、纯剪旳应力--应变关系
z
E
x
z
y
xy
xy
G
i 0 (i x,y,z)
z
yz zx 0
x
x
xy
x
三、复杂状态下旳应力 --- 应变关系
y
y
x
y x
z
xy
z
x
依叠加原理,得:
x
1
(MPa)
解法2—解析法：分析——建立坐标系如图
45 25 3
95
60°
i j
x
2
y
（
x
2
y
）2
2 xy
y
1
25 3 y 45MPa
° 5
0
Ox
6095MPa 6025 3MPa
yx 25 3MPa xy
x ?
x
y
2
sin 2
xy cos 2
25 3 x 45 sin 120o 25 3 cos120o
y
z
z
y
证明: 单元体平衡 M z 0
xy x
x
( xydydz)dx( yxdzdx)dy0
xy yx
五、取单元体： 例1 画出下图中旳A、B、C点旳已知单元体。
F
A
y
F x
x
A
B
C z
x B x
zx
xz
F
Mex
yx
C
xy
FP

第七章应力状态1

第七章应力状态1
30

yx
y
e
x y sin 2 xy cos 2 2
xy
x
300 n
18.3MPa
f
50
(2) 求主应力和主单元体的方位
x = -40MPa， y =60MPa，
tg 2
0


x
2
xy
y
2(50) 1 40 60
xy = -50MPa。

(d)
pD 4t

n
（2）包含直径的纵向截面上的应力 用两个横截面 mm , nn 从圆筒部分 取出 单位长的圆筒研究。
m
n
p
m
1
n
17
由截面法，假想地用 直径平面将取出的单 位长度的圆筒分成两 部分。取下半部分为 研究对象。
包含直径的纵向平面
直径平面
研究对象
R 是外力在 y 轴上的投影， 包含直径的纵截面上的内力为轴力 FN 。 该截面上的应力为正应力 ”，且 假设为均匀分布。
y
t p z
D
（a）
（b）
解：
包围内壁任一点，沿直径方向
取一单元体，单元体的侧面为 横截面，上，下面为含直径的 纵向截面，前面为内表面。 包含直径的纵向截面
横截面
内表面
（1）横截面上的应力 假想地，用一垂直于轴线的平面将汽包分成两部分，取右边为研 究对象。n— n面为横截面 。
n
p
n
图（d）研究对象的剖面图，其上的外力为压强 p。
1 2 3
2
1
3
7
（1）单轴应力状态：只有一个主应力不为零
（2）平面应力状态 ：有个二主应力不等于零。（参见教材定义）

材料力学第七章 应力状态


主平面的方位：
tan
2a0
2 xy x
y
主应力与主平面的对应关系： max 与切应力的交点同象限
例题：一点处的平面应力状态如图所示。
已知 x 60MPa， xy 30MPa, y 40MPa, a 30。
试求（1）a 斜面上的应力； （2）主应力、主平面； （3）绘出主应力单元体。
x y cos 2a
2
x sin 2a
x
a
x y sin 2a
2
x cos 2a
300
10 30 2
10 30 cos 60020sin 600
2
2.32 MPa
300
10 30 sin 600 2
20cos 600
1.33 MPa
a
20 MPa
c
30 MPa
b
n1
y xy
a x
解：（1）a 斜面上的应力
y xy
a
x
2
y
x
2
y
cos 2a
xy
sin 2a
60 40 60 40 cos(60 ) 30sin(60 )
2
2
a x 9.02MPa
a
x
y
2
sin
2a
xy
cos
2a
60 40 sin(60 ) 30cos(60 ) 2
58.3MPa
2
1.33 MPa
300 600 x y 40 MPa
在二向应力状态下，任意两个垂直面上，其σ的和为一常数。
在二向应力状态下，任意两个垂直面上，其σ 的和为
一常数。
证明： a
x y

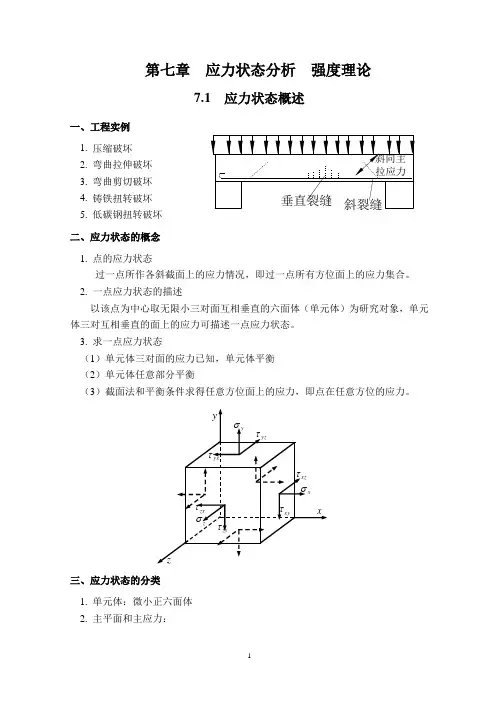
7-第七章 应力状态分析 强度理论.

第七章应力状态分析强度理论7.1 应力状态概述一、工程实例1. 压缩破坏2. 弯曲拉伸破坏3. 弯曲剪切破坏4. 铸铁扭转破坏5. 低碳钢扭转破坏二、应力状态的概念1. 点的应力状态过一点所作各斜截面上的应力情况，即过一点所有方位面上的应力集合。

2. 一点应力状态的描述以该点为中心取无限小三对面互相垂直的六面体（单元体）为研究对象，单元体三对互相垂直的面上的应力可描述一点应力状态。

3. 求一点应力状态（1）单元体三对面的应力已知，单元体平衡（2）单元体任意部分平衡（3）截面法和平衡条件求得任意方位面上的应力，即点在任意方位的应力。

三、应力状态的分类1. 单元体：微小正六面体2. 主平面和主应力：主平面：无切应力的平面主应力：作用在主平面上的正应力。

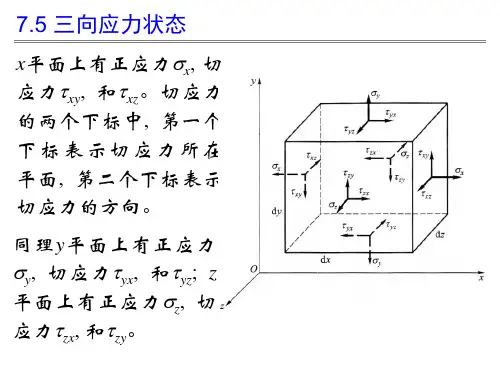
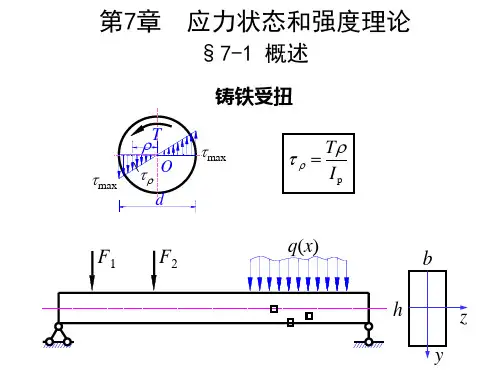
3. 三种应力状态单项应力状态：三个主应力只有一个不等于零，如A 、E 点 二向应力状态：三个主应力中有两个不等于零，如B 、D 点 三向应力状态：三个主应力都不等于零四、应力状态分析的方法 1.解析法2. 图解法7.2应力状态分析的解析法一、解析法图示单元体，已知应力分量x σ、y σ、xyτ和yx τ。

xxx（一）任意截面上的正应力和切应力：利用截面法，考虑楔体bef 部分的平衡。

设ef 面的面积为dA ， ∑=0F n 0sin )Asin (cos )sin A (cos )cos A (sin )cos A (A =-+-+αασααταασαατσαd d d d d y yx x xy∑=0F tsin )Asin (cos )sin A (sin )cos A (cos )cos A (A =++--ααταασαασαατταd d d d d yx y x xy根据切应力互等定理： y x xy ττ=三角函数关系：22cos 1cos 2αα+=，22cos 1sin 2αα-=，∂=cos sin 22sin αα解得：ατασσσσσα2sin 2cos 22x x xy yy--++=（7-1）ατασστα2cos 2sin 2x xy y+-= （7-2）（二）主应力即主平面位置将式（8-1）对取一次导数，并令其等于零可确定正应力的极值和所在平面的位置。

材料力学-应力状态分析


+
σ x σ y
2
cos 2α τ x sin 2α
sin 2α + τ x cos 2α
注意： 的正负号， 注意：1）σx 、σy 、τx 和 α的正负号， 2） 公式中的切应力是τx ，而非τy， 而非 的正负号。 3） 计算出的σα和τα 的正负号。
τα τ α>0
τα τ α<0
图示圆轴中， 已知圆轴直径d=100mm， 轴向拉 例 ： 图示圆轴中 ， 已知圆轴直径 ， 力 F=500kN，外力矩Me=7kNm。求 C点α = 30°截 ， 外力矩 。 点 ° 面上的应力。 面上的应力。 y
σy
τ
D
x
τx τy
σx
o A2
C
A1
σ
D
y
σ1 =
σ x +σ y
2
σ x +σ y + 2
2 +τ x
2
2
σ2 =
σ x +σ y
2
σ x +σ y 2 +τ x 2
σy
τ
D
x
τx τy
σx
o A2
2α0
C
A1
σ
D
y
2τ x 2α 0 = arctan σ x σ y
σ x σ y R= 2
+τ x2
2
σ x +σ y σ α 2
σy
σ x σ y 2 2 + τα = +τ x 2 τ
2 2
D
x
τx τy
σx
o
C D
y
σ
50MPa

第七章_应力状态和强度理论

第 1 页/共 4 页第七章 应力状态和强度理论7-3 横截面上 AF =σ α截面上 αστασσσαα2sin 22cos 22=+=，强度条件 ][432sin 2][)2cos 1(2σατσασαα≤=≤+=A F A F ，等价于 ][2sin 342)2cos 1(2max σαασ≤⎭⎬⎫⎩⎨⎧⋅+=A F A F e ，由0=ασd d e，并比较︒=0α或︒60的e σ，得使e σ最小的角度︒=60α 7-7 内力 m kN M ⋅-=2.7，kN F s 10-=应力 MPa I Myz 55.10==σ，MPa bI S F z z s 88.0*-==τ 主应力 MPa 62.1022221=+⎪⎭⎫⎝⎛+=τσσσ，MPa 073.022223-=+⎪⎭⎫⎝⎛-=τσσσ主平面方位 ︒=⇒=-=74.4167.022tan 00αστα7-8(d) MPa MPa x y x 50200-=-==τσσ，， ︒=45α截面上：MPaMPax yx yy102cos 2sin 2402sin 2cos 22=+-==--=αταστατασσσαα主应力：MPa x y y4122221=+⎪⎪⎭⎫ ⎝⎛+=τσσσ， MPa x y y6122223-=+⎪⎪⎭⎫ ⎝⎛-=τσσσ主平面方位：︒=⇒=--=34.39522tan 00ασταyx7-15(a) MPa z 50=σ——为主应力，另两个主应力由下列应力决定 MPa MPa MPa x y x 403070-===τσσ，，MPa MPa x y x yx x y x yx 3.5227.94222222=+⎪⎪⎭⎫ ⎝⎛--+=''=+⎪⎪⎭⎫ ⎝⎛-++='τσσσσστσσσσσ主应力 MPa MPa MPa z 3.5507.94321=''===='=σσσσσσ，， 最大切应力 MPa 7.44231max =-=σστ7-16(a) MPa MPa MPa 105070321＝，＝，＝σσσ A 点：MPa MPa A A 2030==τσ，在2σ与3σ决定的应力圆上使切使劲达极值7-18 立方体边长 a ＝20mm不计摩擦，各面上的应力为主应力顶面 MPa aF3523-=-=σ，侧面021<=σσ 主应变021==εε，又)]([13211σσνσε+-=EMPa 151321-=-==⇒σννσσ7-21 k 处截面上的内力： e M laM =，l M F e s =应力： bhFb I S F s z z s 230*==＝，τσ︒=45α方向即为主应力方向第 3 页/共 4 页τστσ-==31，主应变 )(131451νσσεε-==︒E由上可得 ︒+=45)1(32ενElbhM e7-22 钢球各点应力状态相同 MPa 14321-===σσσ体应变 )(21321σσσνθ++-=E体积改变 3101054.6m V V -⨯==∆θ7-23 MPa MPa MPa z y x 403070-===σσσ，，MPaMPax y x y x x y x y x 28.54)(21)(2172.944)(21)(212222=+--+=''=+-++='τσσσσστσσσσσ主应力 MPa MPa MPa 28.55072.94321==σσσ，＝， []3213232221/99.12)()()(61m m kN Ev d ⋅=-+-+-+=σσσσσσν7-24 平面应力状态 MPa MPa x y x 15015===τσσ，，主应力 MPa MPa x x x27.9027.242232221-===+⎪⎭⎫ ⎝⎛+=σστσσσ，， 按第一强度理论：][11t r σσσ<= 按第二强度理论：][59.26)(3212t r MPa σσσνσσ<=+-= 满意强度条件。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

t
1 2
(s
x
s y ) sin
2
t xy
cos 2
令:dt 0 d 1
tan21
s
x s 2t xy
y
由上式可以确定出两个相互垂直的平面，分别
为最大切应力和最小切应力所在平面。
ttmmainx
± （sx
sy
2
）2 tx2y
tan
2 0
s
2t xy x s
y
1
0
p
4
, 即极值切应力所在平面 与主平面成 450
t xy sin 2
60 40 60 40 cos(60 ) 30sin(60 )
n
s
t xy
dA
s dA t xy(dAcos )sin s x (dAcos ) cos t yx
t
t yx(dAsin ) cos s y (dAsin)sin 0
sy
Ft 0
t dA t xy(dAcos ) cos s x (dAcos )sin t yx(dAsin )sin s y (dAsin ) cos 0
一、引言
§7–１ 应力状态的概念
1、铸铁与低碳钢的拉、压、扭实验现象是怎样的？
P 铸铁拉伸
铸铁压缩
M
P
低碳钢 扭转
铸铁扭转 P
低碳钢拉伸试验
铸铁拉伸试验
低碳钢扭转试验
铸铁 扭 转 试 验
2、复杂应力状态怎样建立强度条件？
M
ss
s
s t
Fs
t t
简单应力状态的强度条件：
s max [s ]; t max [t ]
N = stl
s =
pD 2t
s
s
s 二向应力状态
s
三向压缩
§7–2 平面应力状态分析——解析法
y
sy
sy
txy sx
等价 y
sx
txy
x z
Ox
1.斜截面上的应力
sx α
y
t yx t xy
x
sy
sx αt
n
s
t xy
dA
t yx
t
sy
Fn 0 Ft 0
列平衡方程
Fn 0
sx αt
s z b、平行平面上应力相等。
t zx t zy
z 0 x
sy
y
t t t yx
t
t xy s x
xz
t xz t xy
t yz s x
zx
t zy
t yz
sy
yx
sz
轴向拉伸
σ
σ
σ
σ
s FN
A
扭转
τ τ
τ τ
t T
Ip
弯曲变形
τ
σ
τσ
s MZy
Iz
σ
τσ
t
Fs
S
* z
IZb
l
例
S
FP
2.正负号规则
s
1 2
(s
x
s y) ຫໍສະໝຸດ 1 2(sx
s y ) cos 2
t xy
sin
2
y x s x α
t yx t xy
t
1 2
(s
x
s y ) sin
2
t xy
cos 2
正应力：拉应力为正；
sy
压应力为负。 切应力：绕微元顺时针方向
α s x
ta
n
sa
t xy
x
t t yx sy
转动为正；反之为负。
例题：一点处的平面应力状态如图所示。
已知 s x 60MPa， t xy 30MPa, s y 40MPa, 30。
试求（1） 斜面上的应力； （2）主应力、主平面； （3）绘出主应力单元体。
sy t xy
sx
解：（1） 斜面上的应力
sy t xy
s
sx
s y
2
sx
s y
2
cos 2
a
l
SF
a
Fa T
M
Fl
S平面 y
1
T
4
z
x
2
1
τ
T Wp
3 Mz
σ
Mz Wz
t
2t
3
τ
T Wp
σ
Mz Wz
四、主单元体、主平面、主应力：
sy
y
主单元体
sx
各平面上切应力均为零的单元体。
sz
z
s2
主平面
切应力为零的平面。 x
主应力
主平面上的正应力。
s1
s3
sy
y
主应力排列规定：
sz
z
s2
sx
强度条件如何建立？
P
M 弯扭组合变形 强度条件如何建立？
F
F
s
s max
F A
s
t
s s cos2
同一点在斜截面上时：
t
s sin 2
2
表明：同一点在不同方位截面上，它的应
力是各不相同的，此即应力的面的概念。
材料力学
Mz Fs
横截面上正应力分析和切应力分析 的结果表明：同一面上不同点的应力各
txz
sx
sx
A
三向（空间）应力状态
s3
s1
s2
材料力学
二向（平面）应力状态
材料力学
y
sx
x
y
t yx t xy
x
单向应力状态
纯剪应力状态
材料力学
三
二
向
向
应
应
力 状
特例
力 状
态
态
单向应力状态 特例 纯剪应力状态
材料力学
二向和三向应力状态实例
sA = sp Dt=P
s
=
pD 4t
s =?
2N=pDl
不相同，此即应力的点的概念。
材料力学
应力
指明
哪一个面上
哪一点？
哪一点 哪个方向面？
二、一点的应力状态
过一点不同方向面 上应力的集合，称 之为这一点的应力 状态。
就是研究一点处沿各个不同方位的截 面上的应力及其变化规律。
三、单元体：单元体——围绕被研究点截取一尺寸为无限小
的正六面体。
单元体的性质——a、各表面上应力均匀分布；
α角：由x 轴正向逆时针转
到斜截面外法线时为正；反 之为负。
s
1 2
(s
x
s
y
)
1 2
(s
x
s
y
) cos
2
t
xy
sin
2
t
1 2
(s
x
s
y
) sin
2
t
xy
cos
2
3. 正应力极值和方向
确定正应力极值
s
1 2
(s
x
s y)
1 2
(s
x
s y ) cos 2
t xy
sin
2
ds d
(s x
s y ) sin
利用三角函数公式
{cos2 1 (1 cos 2 ) 2 sin2 1 (1 cos 2 ) 2
2sin cos sin2
并注意到 t yx t xy 化简得
s
1 2
(s
x
s y)
1 2
(s
x
s y ) cos 2
t xy
sin
2
t
1 2
(s
x
s y ) sin
2
t xy
cos 2
在受力构件中任意一点，必定存
在三个相互垂直的主平面，因此
x 在每一点处必有三个主应力，以
s1，s2 和 s3 表示，且规定
s1
s1s2 s3
s3
三向应力状态
三个主应力都不为零的应力状态。 s2 s1
二向应力状态
一个主应力为零的应力状态。
s3
单向应力状态
一个主应力不为零的应力状态。
sx B sx
tzx
2 0
s
2t xy x s
y
由上式可以确定出两个相互垂直的平面，分别 为最大正应力和最小正应力所在平面。
所以，最大和最小正应力分别为：
s max
sx
s
2
y
1 2
sx
s y
2
4t
2 xy
s min
sx
s y
2
1 2
sx
s y
2
4t
2 xy
主应力按代数值排序：σ1 σ2 σ3
4. 切应力极值和方向
2
2t xy cos 2
设α＝α0 时，上式值为零，即
(s x s y ) sin 20 2t xy cos 20 0
2(σx
σy 2
) si
n
2
α0
τx
yc
os
2
α0
2τα0
0
即α＝α0 时，切应力为零
s
1 2
(s
x
s y)
1 2
(s
x
s y ) cos 2
t xy
sin
2
tan